Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

128

HYPERBOLIC EQUATIONS

Incidentally, the model (4.72) also enables us to give a physical interpretation

of the bicharacteristics that were introduced in §2.6. The Mach cone is simply the

characteristic surface across which any of the flow variables can have a jump in its

second derivatives. Now suppose the bullet is replaced by the slender pointed nose

of an aircraft model and that a thin aerial protrudes from the nose through the

Mach cone. Since the aerial only intersects the cone at one point, it propagates a

discontinuity just along the bicharacteristic through that point which, in this case,

is just the generator of the Mach cone. Any `fatter' object that protrudes through

the Mach cone would generate a new component of the characteristic surface.

As a final remark to lead into the next section, we note that, had we considered

an equation more complicated than 8zu/8tz = 4V2u, such as one with variable

coefficients, then diagrams such as Fig. 4.7 would for small time become more

complicated. In particular, the spherical `waves' in Fig. 4.7 would locally become

ellipsoids whose shape depended on the coefficients in the equation, and the ray

cones would correspondingly have elliptical cross-sections. The geometric complex-

ity would become much worse if the cones were to lose their local convexity; this

cannot happen for scalar second-order equations, but it may for vector equations,

as we shall soon see.

*4.7 Higher-order systems

One of the basic motivations for studying partial differential equations is that so

many everyday phenomena are modelled by systems of such equations. Indeed, in

the preceding sections we have explained how even a scalar hyperbolic equation

can not only underpin much of the science of acoustics but also describe various

other kinds of small-amplitude wave motion. We now consider two other areas of

applied science which lead to vector second-order hyperbolic equations.

4.7.1 Linear elasticity

The first concerns the propagation of acoustic waves in solids, whose modelling

involves some elementary elasticity theory. As is the case for all continuum mechan-

ics, we introduce a vector field u(x, t) to describe the configuration of the medium.

In this case it represents the displacement of a particle from an unstressed reference

configuration, i.e. the particle which is at x in the reference configuration moves

by u(x, t). We also need to model the forces in the medium, and this should be

done by introducing a stress tensor (as, for example, in (40]). Here we side-step this

process by merely noting that elastic solids resist both shear forces (Fig. 4.9(a))

and tensile/compressive forces (Fig. 4.9(b)).

An example of the former would be the shearing of a sheet of rubber with a

displacement u in the x direction that is only a function of y and t. In the simplest

model, we could propose that the shear force per unit area in the sheet is p Ou/Oy,

where µ is the constant `shear modulus', and hence an argument like that used in

§2.1 gives that the equation of motion is

HIGHER-ORDER SYSTEMS 129

Ti +

n-aysy

ai E

a2+

aa2

ca)

(b)

Fig. 4.9 (a) Shear stresses and (b) tensile stresses in an elastic medium.

where p is the density of the sheet. Equally, if we were to stretch a rubber band

along its length so that its displacement is u(x, t) in the x direction, the tensile

force would be A' au/8x and the equation of motion would be

82u _ a r a1L

8t2 8x 8x

where A' is another positive constant. The effect of combining these two mecha-

nisms in order to synthesise the displacement u(x, t) of a general isotropic linearly

elastic solid is not quite a simple summation, because of the coupling between

compression/tension and shear. Hence we simply quote the end result,

p -t?. = (A + 2p)VV u - iV A (V A u),

(4.73)

where p, the shear modulus of the material, is as above and A is related to Young's

modulus A' by A' = µ(3A + 2p)/(A + p).

We are thus confronted with a system of three linear second-order equations,

but there is no reason why we cannot combine the approach used in §2.6 with that

used earlier in this chapter: we simply define m(x, y, z, t) = 0 to be a characteristic

surface if it is one on which the prescription of Cauchy data u and 8u/8n does

not yield a unique local solution. Writing

0 0 e¢

ax, ay, 8z

) =

as in §2.6, we find, after some manipulation, that

(µ(fi +{z +fs) -pa)((A+2ll)(fi +{2 +ts)

=0. (4.74)

Hence, in the language of §2.6, the normal cone comprises two components rather

than the single `sheet' of fluid acoustics in §4.6.2 above. The corresponding ray

130

HYPERBOLIC EQUATIONS

cone also comprises two sheets. This is geometrically obvious from the fact that

the normal cone has concentric circles as cross-sections to = constant, but we can

also compute the ray cone analytically; from the prescription in (2.54)-(2.56), it

is given parametrically by

z At,=

AC2=z-A£3

+Ado=0,

p p A p

and

-Alt. =

-A= z

-AA3

+Ai; =0

o ,

A+2p

A+2p A+2p

(x2 + y2 + z2 - c8t2)(x2 + y2 + z2 - yt2) = 0, (4.75)

where c; = p/p and y = (A+2p)/p are the so-called `S' and `P' wave speeds. The

physical interpretation is that acoustic waves in an elastic solid can propagate at

two distinct velocities, as is apparent from seismograph traces.48

This example shows us that, if we wish to generalise the arguments about

hyperbolicity given at the end of §4.6 to higher-order systems, we must be prepared

to consider 'multi-sheeted' normal and ray cones rather than the single-sheeted

cones of Fig. 4.8. Fortunately, both the cones (4.74) and (4.75) consist of two

`nested' convex cones, and energy estimates like those mentioned in Exercise 4.13

can be used to prove well-posedness of the solution whenever Cauchy data is

prescribed on a space-like surface, i.e. on one that lies `outside' the outer sheet of

the ray cone; this implies that the normal to a conical space-like surface always

lies in a time-like direction inside the outer sheet of the ray cone. As in §4.6, this

geometry provides a strong motivation for the definition of hyperbolicity for higher-

order systems to be associated not only with the system of partial differential

equations but also with the relevant time- and space-like directions in the space of

the independent variables. However, the fact that (4.74) has two components now

opens up the possibility that their union might not be convex, and we will return

to this situation at the end of this section.

Finding solutions of (4.73) in practical situations entails many serious technical

details, especially when it comes to applying boundary conditions. One common

approach is to consider solutions in the form

u = t (u'(x)e i"t)

for w E U,

where u' satisfies an equation in the so-called frequency domain with only three

independent variables. However, this latter equation is no longer hyperbolic and

will be dealt with in the next chapter. Whether we deal with systems in the

real time domain or the frequency domain by transform methods, we inevitably

encounter difficulties caused by having to consider the Fourier inversion of rational

functions involving high-degree polynomials (sextic in this case). Hence we will not

consider any explicit solutions in this chapter.

4aln fact, earthquake recording is complicated by the presence of the stress-free boundary of

the earth, which is responsible for generating a third wave speed, as shown in Exercise 4.16.

HIGHER-ORDER SYSTEMS 131

4.7.2

Maxwell's equations of electromagnetism

We conclude by mentioning perhaps the most famous of all higher-order systems

of linear partial differential equations, Maxwell's equations of electromagnetism.

Despite their importance, these equations are far more difficult to explain than

any we have yet encountered. Hence, we will only give a brief account of their

derivation. The starting point is Faraday's law of induction, which concerns the

basic mechanism for dynamos and aerials. It says that any time-varying magnetic

flux through a closed loop L produces an electric field E around L, and is easy to

verify in a laboratory where, if L is a conductor, the electric field drives a current

round it. Denoting the magnetic field by H, the rate of change of magnetic flux

through L, i.e.

011

ffH.dS=JJ.dSwhere

D spans L. If L happens to be a conductor, t

he electric field generated

drives a current round L which, by Ohm's law, is itself proportional to

fE.dx=JJVAE.dS.

Thus, since D is arbitrary, 8H/Ot oc V A E. The constant of proportionality turns

out to be negative and the equation is usually written as

VAE= -p

. (4.76)

However, the electric field is generated whether or not L is conducting and Maxwell

proposed that this, the first of his equations, should hold everywhere and not just

for conductors in which E is associated with a current.

The second, and even more intuitive, of Maxwell's equations comes from an-

other experimental observation. This is the Biot-Savart law, which asserts that

a current j flowing steadily along a straight wire creates a magnetic field H az-

imuthally around the wire and that its strength decays inversely with the square of

the distance from the wire. Hence the magnetic field H(x) caused by any current

loop L is proportional to

- /' (x-x')Adx'

Ix - x113

(4.77)

in the usual units the constant of proportionality is 1/41r. It is then plausible to

propose that, for an arbitrary steady spatially-distributed current j,

VAH=j, (4.78)

but we will have to wait until Chapter 5 before we can see why (4.77) can be

viewed as the 'solution' of (4.78).

The Biot-Savart law does not allow for the effects of time-varying currents or

charge distributions but, if we assume conservation of charge, we must ensure that

132

HYPERBOLIC EQUATIONS

j is related to the charge density p by an equation analogous to the conservation

laws mentioned in §2.1. Thus,

+ V j = 0.

(4.79)

However, in the same way that the divergence of a gravitational force field is

proportional to the local mass density, we can propose that

(4.80)

where e is a constant called the permittivity. Maxwell's great contribution was to

assert that the effect of time dependence is to change (4.78) to

VAH=j+fO,

(4.81)

thereby ensuring consistency with (4.79).49

We are not quite finished, as it can be seen from the partial differential equation

point of view that an additional scalar equation for H is necessary for us to have

any hope of uniqueness. To see this, let us restrict ourselves to free space where

there is no charge and no current, so that

VAH=e

and

VAE=-µ8t.

(4.82)

Although these are six equations for six unknowns, the degeneracy of the curl

operator means that, using these equations alone, E and H can each only be

determined to within the gradient of a scalar, time-independent function. However,

(4.80) gives50

(4.83)

which removes the non-uniqueness in E, and a similar scalar equation is also

necessary for H. Fortunately, the consequence of the commonly-held belief that

there are no magnetic monopoles is that

V H = 0,

(4.84)

which, unlike (4.83), holds even in the presence of charges or currents.

49We must warn the reader that (4.76) and (4.81) are usually derived much more fundamentally

in physics texts in terms of the so-called magnetic induction B and displacement current D rather

than H and E, respectively. In many practical situations the distinction Is fortunately irrelevant

from the mathematical standpoint.

50We remark that V E = 0 is also true to a good approximation in many cases of steady

current flow, for example in metals. In such situations we can often use the bulk version of Ohm's

law, j = oE, where or is a material property called the electrical conductivity, to show from (4.79)

and (4.80) that

5i +E(op+Ve-E)=0;

when o is constant, we must have p = 0 (indeed, any initial charge density decays on the time-

scale c/o). It is only when u has large spatial variations that charge can accumulate; an example

of this is the surface charge layer that can occur when or jumps between a conductor and an

insulator.

HIGHER-ORDER SYSTEMS 133

Combining these equations and using the identity V A VA =

V2 gives

that, in a vacuum,

(L2

t2 -CV)

H = (8t2 -

C2V2)

E = 0,

where c2

and hence the magnetic and electric fields both satisfy vector

wave equations with speed of propagation c, the velocity of light. From previous

arguments, both equations are hyperbolic with time-like directions in x2+y2+z2 <

c2 t2 (the normal cone is c2 ({1 + t2 + t3) - &o = 0) but, combined as a sixth-order

system for H and E, we find a mathematical degeneracy because the normal cone

does not have distinct components.

The examples above from acoustics and electromagnetism give us an excellent

physical framework in which to interpret characteristic surfaces in multi-variable

partial differential equations. These `manifolds' O(x, y, z, t) = 0 are, as we know,

surfaces across which discontinuities in the second derivatives of the dependent

variable can propagate. Hence, it is natural to think of them as 'wave-fronts', as

we did in Fig. 4.8. Many people also have a good physical intuition about light

rays and sound rays but it can sometimes be quite difficult to identify such rays

with the generators of the ray cone in any time-dependent propagation problem.

One difficulty, at which we have already hinted, is that the normal cone may not

be nested or convex, as it was for linear elastic waves or electromagnetic waves in

a vacuum. A commonly occurring configuration is that of two cones of elliptical

cross-section, as in Fig. 4.10, and, indeed, this geometry can be shown to arise

when a sufficiently anisotropic electromagnetic medium is modelled by replacing

E in (4.82) by a suitable constant matrix multiplied by E. Now suppose we try

to calculate the ray cones in such a situation. The ray cones corresponding to the

Fig. 4.10 Normal cones for an anisotropic medium; Co = t, 41 = x and (2 = y.

134

HYPERBOLIC EQUATIONS

All

(c)

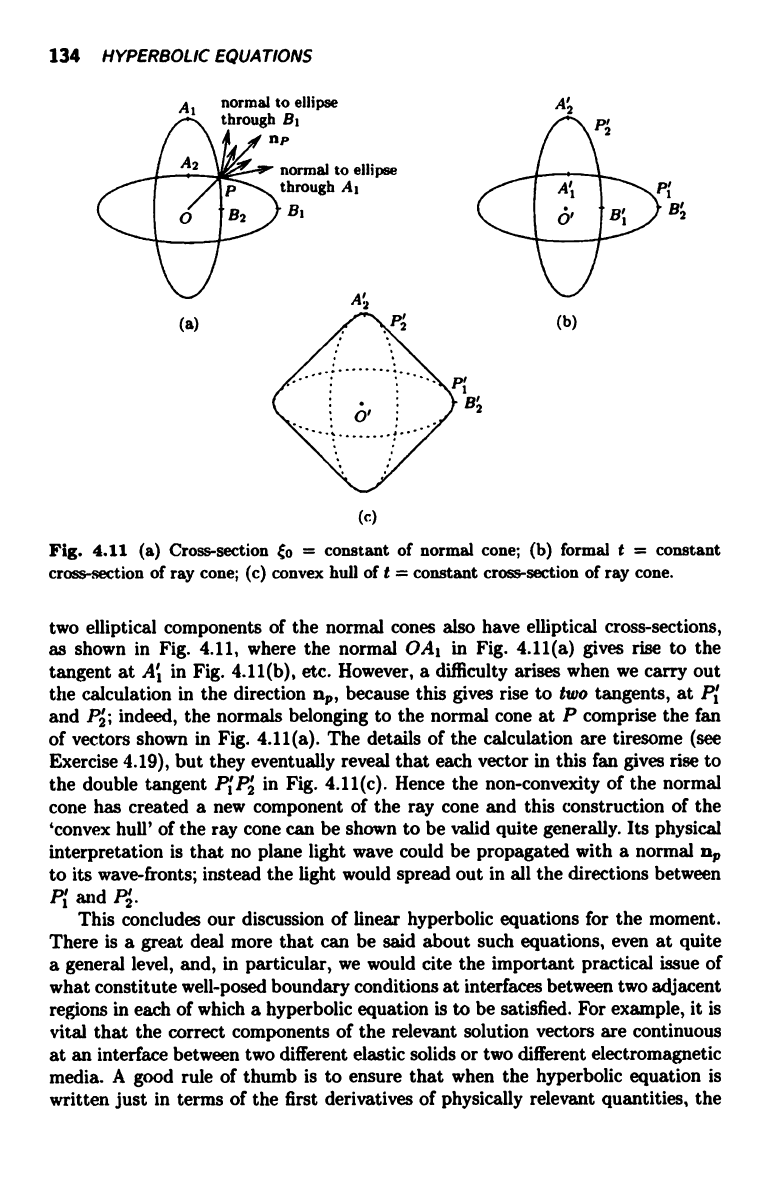
Fig. 4.11 (a) Cross-section to = constant of normal cone; (b) formal t = constant

cross-section of ray cone; (c) convex hull of t = constant cross-section of ray cone.

two elliptical components of the normal cones also have elliptical cross-sections,

as shown in Fig. 4.11, where the normal OA, in Fig. 4.11(a) gives rise to the

tangent at Ai in Fig. 4.11(b), etc. However, a difficulty arises when we carry out

the calculation in the direction np, because this gives rise to two tangents, at Pi

and Pa; indeed, the normals belonging to the normal cone at P comprise the fan

of vectors shown in Fig. 4.11(a). The details of the calculation are tiresome (see

Exercise 4.19), but they eventually reveal that each vector in this fan gives rise to

the double tangent P1P2' in Fig. 4.11(c). Hence the non-convexity of the normal

cone has created a new component of the ray cone and this construction of the

`convex hull' of the ray cone can be shown to be valid quite generally. Its physical

interpretation is that no plane light wave could be propagated with a normal np

to its wave-fronts; instead the light would spread out in all the directions between

PP and Pz.

This concludes our discussion of linear hyperbolic equations for the moment.

There is a great deal more that can be said about such equations, even at quite

a general level, and, in particular, we would cite the important practical issue of

what constitute well-posed boundary conditions at interfaces between two adjacent

regions in each of which a hyperbolic equation is to be satisfied. For example, it is

vital that the correct components of the relevant solution vectors are continuous

at an interface between two different elastic solids or two different electromagnetic

media. A good rule of thumb is to ensure that when the hyperbolic equation is

written just in terms of the first derivatives of physically relevant quantities, the

NONLINEARITY 135

`integration by parts' or `weak solution' identities such as (2.43) are satisfied. An

illustration of this can be found in Exercise 4.17.

4.8

Nonlinearity

We have already seen in Chapter 1 that the presence of nonlinearity usually results

in fundamental changes in the properties of solutions of previously linear partial

differential equations. While, as a general rule, every nonlinear equation needs to

be treated on its own merits, there are just a few general statements that can be

made and general techniques that can be tried. Of course, when these techniques

apply, they are worth their weight in gold.

There is one approach that is peculiar to hyperbolic equations, where we have

seen that a common effect of nonlinearity is that of shock formation as a result of

characteristics intersecting. But, before such catastrophes occur, there may be the

following possibilities.

4.8.1

Simple waves

We remarked in Chapter 2 that characteristics are usually of little value in ob-

taining explicit solutions of hyperbolic systems. Even for a scalar second-order

quasilinear equation with two independent variables, it is very unlikely that we

can find Riemann invariants, i.e. functions of x, y, u, flu/8x and flu/fly that are

constant on a family of characteristics. Moreover, when such a happy circumstance

does occur, the initial and boundary conditions almost certainly do not prescribe

the values of these invariants. However, one situation exists where we can always

make progress, and it occurs surprisingly often in practice: it is when we consider

the effect of a sudden change in the boundary data on a solution that is trivial

before the change occurs. A prototypical example is that of two-dimensional gas

flow with speed U. and Mach number M,o > 1 past an initially straight wall

(Figs 4.12 and 4.13). The relevant nonlinear hyperbolic equation is

(a)

(b)

Fig. 4.12 (a) Smooth and (b) abrupt expansion of a gas flow.

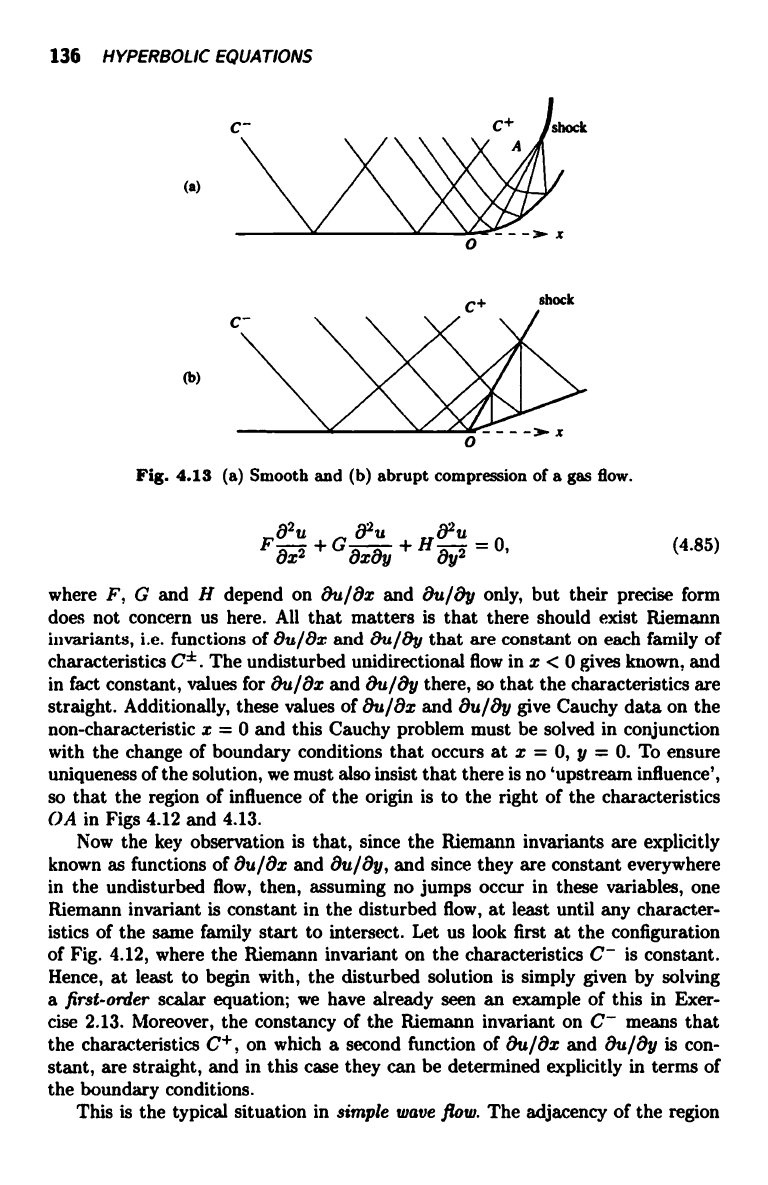
136 HYPERBOLIC EQUATIONS

(a)

(b)

Fig. 4.13 (a) Smooth and (b) abrupt compression of a gas flow.

82U

Ox2

+ G

8xOy

+ H

ay2

= 0, (4.85)

where F, G and H depend on Ou/8x and Ou/8y only, but their precise form

does not concern us here. All that matters is that there should exist Riemann

invariants, i.e. functions of Bu/8x and Ou/8y that are constant on each family of

characteristics C*. The undisturbed unidirectional flow in x < 0 gives known, and

in fact constant, values for On/8x and &u/8y there, so that the characteristics are

straight. Additionally, these values of 8u/8x and Ou/Oy give Cauchy data on the

non-characteristic x = 0 and this Cauchy problem must be solved in conjunction

with the change of boundary conditions that occurs at x = 0, y = 0. To ensure

uniqueness of the solution, we must also insist that there is no `upstream influence',

so that the region of influence of the origin is to the right of the characteristics

OA in Figs 4.12 and 4.13.

Now the key observation is that, since the Riemann invariants are explicitly

known as functions of 8u/8x and Ou/Oy, and since they are constant everywhere

in the undisturbed flow, then, assuming no jumps occur in these variables, one

Riemann invariant is constant in the disturbed flow, at least until any character-

istics of the same family start to intersect. Let us look first at the configuration

of Fig. 4.12, where the Riemann invariant on the characteristics C- is constant.

Hence, at least to begin with, the disturbed solution is simply given by solving

a first-order scalar equation; we have already seen an example of this in Exer-

cise 2.13. Moreover, the constancy of the Riemann invariant on C- means that

the characteristics C+, on which a second function of On/8x and 8u/8y is con-

stant, are straight, and in this case they can be determined explicitly in terms of

the boundary conditions.

This is the typical situation in simple wave flow. The adjacency of the region

NONLINEARITY 137

of interest to a region in which the solution has known constant values for its

Riemann invariants means that the order of the problem can be reduced, which

often means that it can be solved explicitly.

In either the smooth or sharp geometries in Fig. 4.12, the C+ characteristics

form what is called an expansion fan. However, when the geometry is as in Fig. 4.13,

these C+ characteristics converge and eventually a shock forms; in the extreme

case of an abrupt comer, as in Fig. 2.14, this shock is initiated at the corner.

The configuration of Fig. 4.12(b) is interesting because the characteristics in

the fan are y/x = constant and we find that Vu only depends on y/x, not on x or

y independently. Following the derivation of (4.15), this is our second encounter

with what we will call a similarity solution in Chapter 6, because the solution at

(x, y) is effectively the same as that at (Ax, Ay) for any constant A. We will see later

that, if such an invariance exists, it can always be used to find certain solutions of

a partial differential equation in m independent variables as solutions of a related

equation with m - 1 independent variables.

Finally, it is interesting to note that combinations of straight shocks and expan-

sion fans of the type described above, so-called N-waves, are sometimes found to

describe the asymptotic behaviour of the solution of Cauchy problems for general

hyperbolic equations. For example, it can be shown that as t -- oo the solution of

8u 8

+ ex f(u)=O for -oo < x < oo, t > 0,

with u(x, 0) = uo(x) and f convex (i.e. d2 f /dxa > 0), tends to an N-wave as

t -+ oo, with the number of shocks being related to the number of maxima of uo.

Unfortunately, gasdynamic flows involving interacting simple waves, or more

general partial differential equations with three or more independent variables,

rarely admit such simple solutions. However, gas dynamics suggests one other

powerful technique which applies to some more general problems, hyperbolic or

otherwise.

4.8.2 Hodograph methods

Suppose we have a second-order scalar hyperbolic equation in two variables (such

as the transonic flow model (3.12)) whose coefficients depend only on the first

derivatives of u. It is natural to consider a change of independent variables to

(8u/8x, 8u/8y), but what would be the best choice of a dependent variable in

such a case?

We can answer this question geometrically. If we think of the solution u(x, y)

as a surface S in (u, x, y) space and ask how to define w so that the surface

w = w(Ou/Ox, 8u/8y) in (w, $u/8x, 8u/8y) space is as closely related to S as

possible, we recall `geometric duality'. In this concept, instead of only regarding a

surface as a collection of points satisfying u = u(x, y), we equally regard it as the

envelope of its tangent planes

(x - xo)(xo,yo) + (y - yo)y(xo,yo) = u - uo,