Обработка материалов давлением. Сборник научных трудов. №19

Подождите немного. Документ загружается.

Обработка материалов давлением №1 (19), 2008

101

и значения максимальной температуры

через температуру

T :

()

TT −+= ; (6)

через температуру

T :

()

TT −+= . (7)

Очевидно, что величины

, определяемые из равенств (4) и (5), в любой момент

времени охлаждения должны быть одинаковы. Аналогично должны быть одинаковы величи-

ны

T , определяемые из равенств (6) и (7).

На основании известного решения двустороннего охлаждения пластины толщиной

получаем для изменения температур на сторонах фиктивных пластин толщинами

()

R2 δ−

2δ

()

−

следующие зависимости от времени охлаждения τ :

()

⎟

⎠

⎞

⎜

⎝

⎛

τ⋅

−Μ⋅−+=

11BB1

pexpTTTT;

()

⎟

⎠

⎞

⎜

⎝

⎛

τ⋅

δ−

−Μ⋅−+=

33BB3

pexpTTTT;

()

⎟

⎠

⎞

⎜

⎝

⎛

τ⋅

δ−

−Μ⋅−+=

22BB2

pexpTTTT;

()

⎟

⎠

⎞

⎜

⎝

⎛

τ⋅

−Μ⋅−+=

44BB4

pexpTTTT , (8)

где коэффициенты

Μ и p для каждой из сторон можно для малых значений Bi (ох-

лаждение на воздухе) аппроксимировать по табличным значениям [2]:

iii

Bi08,0Bi35,01 +−=Μ ; (9)

Bi2,0Bi94,0p += ; .4,...1i

(10)

Здесь величины

определяются выражениями (2).

Далее расчет температурного поля внутри мотка выполняется с помощью вычисли-

тельной итерационной процедуры для каждой из пластин в функции времени

τ .

Вначале для пластины толщиной

подбираем

таким образом, чтобы добиться

равенства

T по выражениям (4) и (5), затем подбираем

таким образом, чтобы добиться

равенства

по выражениям (6) и (7). Аналогичные процедуры выполняются для каждого

следующего момента времени. В результате получаем зависимости от времени интересую-

щих нас величин:

()

T ,

()

T ,

()

(

)

T ,

(

)

T ,

(

)

T ,

(

)

(

)

Затем определяются относительные безразмерные температуры:

()

(

)

−

=τθ

;

()

(

)

−

=τθ

;

()

−

=τθ

;

()

(

)

−

=τθ

; (11)

()

−

−τ

=τθ

;

()

(

)

−

=τθ

Теперь можно, воспользовавшись теорией перемножения решений [1], получить от-

носительные безразмерные температуры

, в характерных точках сечения прямоугольного

сечения стержня (мотка):

Обработка материалов давлением №1 (19), 2008

102

В вершине А:

(

)

(

)

(

)

⋅

21A

; (12)

В вершине

В:

(

)

(

)

(

)

⋅

32B

; (13)

В вершине

С:

(

)

(

)

(

)

⋅

43C

; (14)

В вершине

(

)

(

)

(

)

⋅

41D

; (15)

В точке 1X :

(

)

(

)

(

)

⋅

11X

; (16)

В точке

3X :

(

)

(

)

(

)

⋅

R33X

; (17)

В точке

2Y :

(

)

(

)

(

)

⋅

H22Y

; (18)

В точке 4Y :

(

)

(

)

(

)

⋅

H44Y

; (19)

В точке XY :

(

)

(

)

(

)

⋅

. (20)

Переход от относительных безразмерных температур к фактическим температурам в

характерных точках сечения осуществляется простым пересчетом:

() ( )

(

)

⋅

−+

Μ jBBj

TTTT , XY,4Y,2Y,3X,1X,D,C,B,Aj

(21)

где

()

τθ

– относительная температура из выражений (12÷20);

()

T – соответствую-

щая ей фактическая температура той же точки сечения.

Таким образом, разработанная математическая модель и вычислительная итерацион-

ная процедура, позволяют определить температурное поле (характерные точки) сечения мот-

ка в функции времени.

Остальные точки температурного поля каждой из сторон сечения лежат на нисходя-

щих ветвях парабол, проведенных из точки с максимальной

температурой на стороне к тем-

пературам вершин, примыкающих к стороне. Например, для стороны 2, параболы нисходят

от

T к

T и

T . Для сечений

()

3X1X

(

)

2Y4Y

закономерность аналогична, так для

сечения

()

3X1X ÷ параболы исходят от

T к

T и

T, а для сечения

()

2Y4Y ÷ – от

T и

T .

Полученные значения температур характерных точек сечения мотка

()

T достаточно

полно представляют закономерности послойного распределения температур в теле мотка при

его остывании.

Для определения эквивалентных коэффициентов теплопроводности

λ и температу-

ропроводности

a представляем моток как тело волокнистого строения с воздушной про-

слойкой, для которого разработана методика определения указанных параметров [2].

Принимая коэффициент теплопроводности стали

в диапазоне температур

C750600

− постоянным и равным

(

)

градчасмккал23

⋅

, а коэффициент пористости мотка

35,03,0 −=ρ , по соответствующим формулам и графикам указанного источника полу-

чим:

()

градчасмккал22

⋅

⋅=λ .

Принимая среднюю теплоемкость стали в том же диапазоне температур постоянной и

равной

()

градкгккал15,0 ⋅ , получим по тому же источнику: часм025,0a

= .

Коэффициент теплоотдачи при охлаждении тел на воздухе излучением и свободной

конвекцией зависит от температуры тела. В диапазоне температур C750600

− для верти-

кально расположенной поверхности можно принять [2]:

(

)

градчасмккал8050

⋅⋅÷≈α .

Для горизонтально расположенной поверхности за счет увеличения теплоотдачи кон-

векцией значение

α больше приблизительно на

(

)

градчасмккал54

⋅⋅÷ . Основываясь на

этих данных, можно ориентировочно принять для мотка:

(

)

градчасмккал8050

⋅⋅÷≈α ;

(

)

градчасмккал8555

⋅⋅÷≈α

Обработка материалов давлением №1 (19), 2008

103

Для внутренней поверхности мотка, излучающей тепло в полузамкнутом объеме с за-

трудненной конвекцией воздуха, очевидно, значение

необходимо принять, по крайней

мере, в два раза меньше, чем

α , т.е.:

(

)

градчасмккал4025

⋅⋅÷≈α .

Нижняя поверхность мотка осуществляет теплоотдачу в большей мере через контакт с

рольгангом и транспортером, чем через излучение и конвекцию. Ориентировочно примем:

(

)

градчасмккал4530

⋅⋅÷≈α .

Адекватность модели реальному процессу обеспечивалась уточнением коэффициен-

тов теплоотдачи с поверхностей мотка

так, чтобы кривые охлаждения характерных точек

мотка в модели соответствовали экспериментальным кривым.

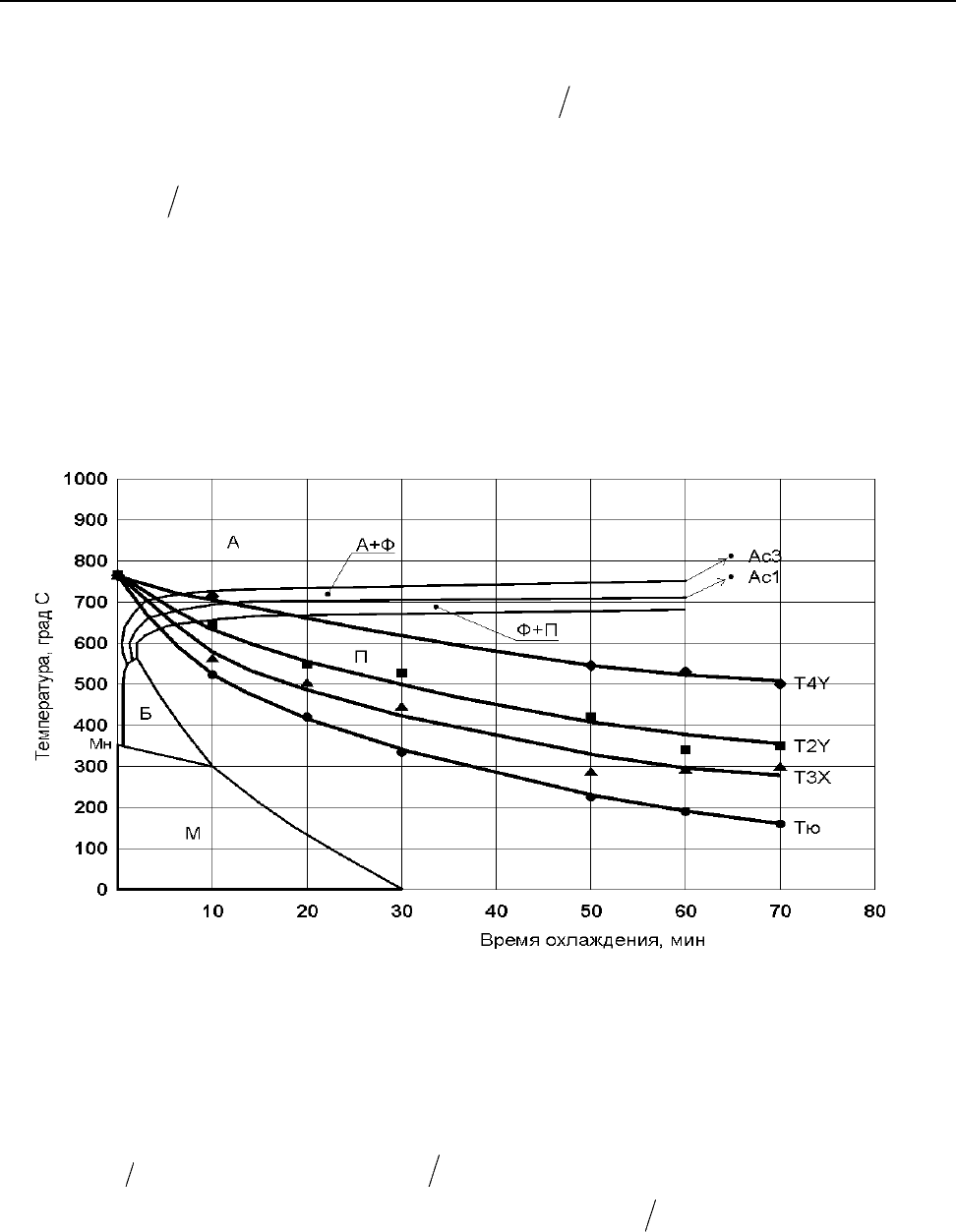
На рис. 2. представлены аппроксимированные экспериментальные кривые охлажде-

ния поверхностей мотка, на которые наложены кривые термокинетической диаграммы пре-

вращения аустенита в стали марки

X45 [3]. Области диаграммы имеют обозначения: А – ау-

стенит, Ф – феррит, П – перлит, Б – бейнит, М – мартенсит.

Так, при параметрах мотка

м3,1D

, м9,0D

м7,0H

, C765T

= , темпера-

туре окружающей среды C30T

= и эквивалентных теплофизических параметрах

()

градчасмккал22

⋅⋅=λ и часм025,0a

= одноименных кривые охлаждения достаточно

близко совпадали при

=α , 70

=α , 65

(

)

градчасмккал30

⋅⋅=α .

Результаты моделирования позволяют представить распределение температуры по-

слойно внутри мотка в любой момент времени. Картина такого распределения через 20 мин

после начала охлаждения, т.е. сразу же после завершения превращения аустенита в стали,

представлена на рис. 3. Распределение носит сложный периодический характер с периодом,

равным высоте слоя, т.е. высоте

мотка H.

Рис. 2. Аппроксимированные экспериментальные кривые охлаждения поверхностей

мотка.

Обработка материалов давлением №1 (19), 2008

104

При направлении слоя по мотку снизу вверх (ход укладчика вверх) отсчет температур

слоев начинается с уровня температур низа мотка на огибающей

AX1D

TTT −

−

. Максимумов

температуры слоев достигает на уровне температур примерно середины высоты мотка на

огибающей

Y2XYY4

TTT

−

. Минимумов температуры слоев достигает на уровне темпера-

тур верха мотка на огибающей

BX3C

TTT

−

− . При направлении слоя сверху вниз (ход уклад-

чика вниз) отсчет температур слоев начинается, наоборот, с огибающей температур верха

мотка – через середину – к низу мотка.

Огибающие описываются приблизительно ветвями парабол с максимумами в центре

сечения мотка. Правая ветвь спадает ниже левой, что вызвано большей теплоотдачей с на-

ружной поверхности мотка.

Как

следует из рис. 3, в пределах одного слоя разница температур может достигать

200

С при общем снижении от внутренних к наружным слоям около 50-60

С. Соответст-

венно, этим колебаниям температур отвечают разные скорости охлаждения участков слоев,

разная дисперсность продуктов превращения аустенита стали и, следовательно, различные

механические свойства.

Из анализа результатов моделирования можно сделать вывод, что основной разброс

механических свойств товарного проката в мотках имеет послойно-периодический характер.

Уменьшение разброса механических свойств товарного проката в пределах

мотка может

быть достигнуто путем уменьшения теплоотдачи с верхней торцевой поверхности мотка, на-

пример, за счет установки экрана над отводящим транспортером.

ЛИТЕРАТУРА

1. Исаченко В.П. Теплопередача. / В.П. Исаченко, В.А. Осипова, А.С. Сукомел–2-е изд. – М.: Энергия,

1969. – 440 с.

2. Тайц Н.Ю. Технология нагрева стали. –2-е изд. – М.: Металлургиздат, 1962. – 567 с.

3. Попов А.А., Попова Л.Е. Справочник термиста. – М.: Машгиз, 1961. – 430 с.

Куваев В. Н. – д-р техн. наук, старший научный сотрудник НГУ;

Чигринский В. А. – канд. техн. наук, старший научный сотрудник НГУ;

Иванов Д. А. – старший научный сотрудник НГУ;

Политов И. В. – старший научный сотрудник НГУ;

Куваев Я. Г. – канд. техн. наук, старший научный сотрудник НГУ;

Щур В. А. – начальник цеха ОАО

«АрселорМиттал Кривой Рог».

НГУ – Национальный горный университет, г. Днепропетровск.

info@dmmi.edu.ua

Рис. 3. Распределение температуры послойно внутри мотка через 20 мин после нача-

ла охлаждения (стрелки – направления движения укладчика витков).

Обработка материалов давлением №1 (19), 2008

105

УДК 621.967.3

Боровик П. В.

Луценко В. А.

Ульяницкий В. Н.

МОДЕЛИРОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ КОНТАКТНОЙ

ПОВЕРХНОСТИ ПРИ ГОРЯЧЕЙ РЕЗКЕ НА НОЖНИЦАХ

В условиях промышленного производства для обеспечения максимальной пропускной

способности участка резки толстолистовых станов наиболее эффективным является исполь-

зование дисковых ножниц в совокупности с внедрением процессов горячей резки, что позво-

ляет повысить технологические возможности существующего оборудования, за счет расши-

рения сортамента разрезаемых листов. Однако на сегодняшний день данная технология со-

держит

скрытые резервы, выявление которых позволит дополнительно увеличить толщину

листов допускаемых к резке на ножницах.

Проводившиеся ранее эмпирические исследования процессов горячей резки металла

на ножницах [1, 2] показали эффективность уменьшения ширины режущей кромки ножа, по-

скольку это приводит к снижению удельной работы резания и как следствие к снижению си-

лы резки.

Очевидно, что всестороннее

теоретическое изучение данного вопроса будет способст-

вовать дальнейшему совершенствованию технологии горячей резки толстолистовых раска-

тов на ножницах за счет уточнения параметров процесса в более широком диапазоне марок

сталей и толщин разрезаемых листов.

Задачей данной работы является расширение представления о напряженном состоя-

нии контактной поверхности инструмента с целью расширения сортамента листов

разрезае-

мых в горячем состоянии, за счет снижения энергосиловых параметров процесса резки в ре-

зультате изменения конструкции режущего инструмента.

Учитывая особенности процесса резки и опираясь на известные решения подобных

задач [3], можно утверждать, что в точке прекращения контактного взаимодействия нор-

мальное контактное давление можно считать равным пределу текучести разрезаемого мате-

риала

()

=0.

В тоже время в вершине ножа имеет место сингулярность напряжений и нормальное

давление теоретически может быть равным бесконечности. Однако практически данная ве-

личина имеет конечное значение, которое может быть определено:

()

(

)

τεε

εετσβ

0max

+= , (1)

где

– относительная ширина контактной площадки при относительном внедрении

;

k – коэффициент усиления сопротивления срезу в вершине ножа;

max

– максимальное сопротивление резанию (имеет место при сколе

= );

– степенной показатель, характеризующий форму распределения сопротивления

срезу в зависимости от относительного внедрения

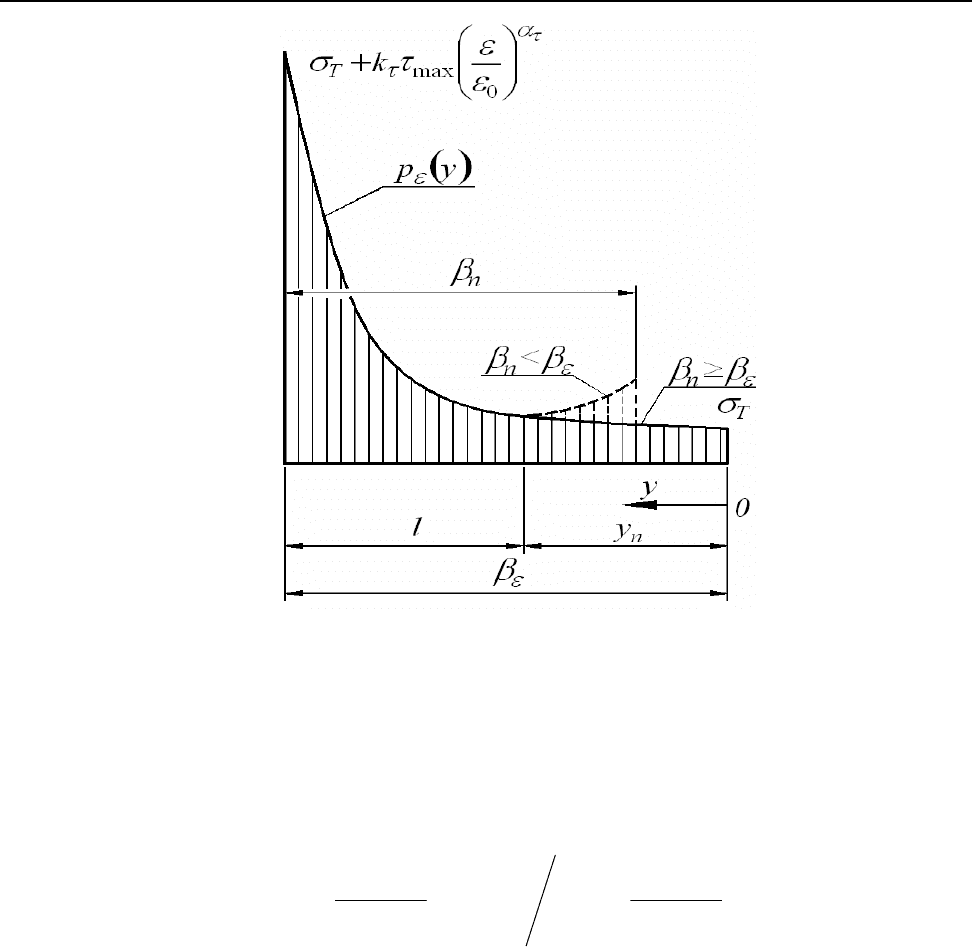
Распределение нормального давления

(

)

по поверхности контакта (рис. 1) на глу-

бине относительного внедрения

можно представить как степенную функцию вида:

()

(

)

(

)

ετ

τε

βεετσ

ykyp

T 0max

+= , (2)

где

– текущая относительная координата контактной поверхности от точки пре-

кращения контактного взаимодействия

(

)

y до вершины ножа

(

)

y ;

– степенной показатель, характеризующий распределение контактного давления

вдоль

на соответствующей величине относительного внедрения.

Обработка материалов давлением №1 (19), 2008

Рис. 1. Схема распределения нормального давления по поверхности контакта.

Также следует принять, что между контактной поверхностью ножа и материала

скольжение отсутствует, поскольку при температуре

C°800650K

коэффициент трения со-

ставляет

5,0≈ [4].

Степенной показатель

можно найти из условия равновесия между удельным со-

противлением резанию

[5] и удельным контактным давлением

. В результате получим:

⎥

⎦

⎤

⎢

⎣

⎡

ετ

εσ

+−ε

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

ετ

εσ

−ε−=α

ετ

max

1k1

. (3)

Принимаем, что коэффициент усиления

k не зависит от относительного внедрения

ножей в металл и является величиной постоянной, определяемой механическими свойствами

разрезаемого материала.

В общем случае связь между пределом текучести материала и относительным внедре-

нием ножей

ε до наступления пластического течения представляется соотношением:

, (4)

где E

– модуль упругости разрезаемого материала, который при температурах

C800650 °K

для большинства сталей равен

(

)

102,16,1E ⋅= K МПа [6].

Однако, учитывая сингулярный характер напряжений в вершине ножа, необходимо в

выражение (4) предел текучести умножить на коэффициент усиления

Учитывая, что на глубине относительного внедрения

ширина контактной поверх-

ности мала, можно допустить равномерное по всей ее ширине распределение условного кон-

тактного давления p, что возможно при 0

, т.е. числитель выражения (3) должен быть

равен нулю. В результате получим:

Обработка материалов давлением №1 (19), 2008

107

(

)

σε= eEk

, (5)

где ξ

– показатель степени, определяемый выражением:

()

TmaxmaxT

0maxmax

+α

⎥

⎦

⎤

⎢

⎣

⎡

+ασβ−τσ

ετβ+α

−

=ξ

, (6)

где

ξ – показатель степени, равный:

()

⎥

⎦

⎤

⎢

⎣

⎡

ε+α

=ξ

. (7)

Таким образом, уравнения (1)

–(7) представляют собой алгоритм для получения рас-

четных эпюр распределения контактного давления

p в зависимости от относительного вне-

дрения

и соответствующего значения коэффициента пропорциональности

β .

Результаты численной реализации данного алгоритма приведены на рисунке 2а для

марки стали 16ГС при температуре

C800° . Анализ показывает, что работа резки преимуще-

ственно выполняется на участке, примыкающем к вершине режущей кромки ножа, ширина

которого составляет H1,0≈ . В тоже время, оставшаяся часть контактных давлений выполня-

ет преимущественно работу по деформированию и отгибу отрезаемой кромки. Из этого сле-

дует, что уменьшение контактной поверхности между ножом и металлом

, путем изменения

конструкции ножа, будет способствовать снижению работы, выполняемой в процессе резки,

за счет локализации зоны пластической деформации отрезаемой кромки.

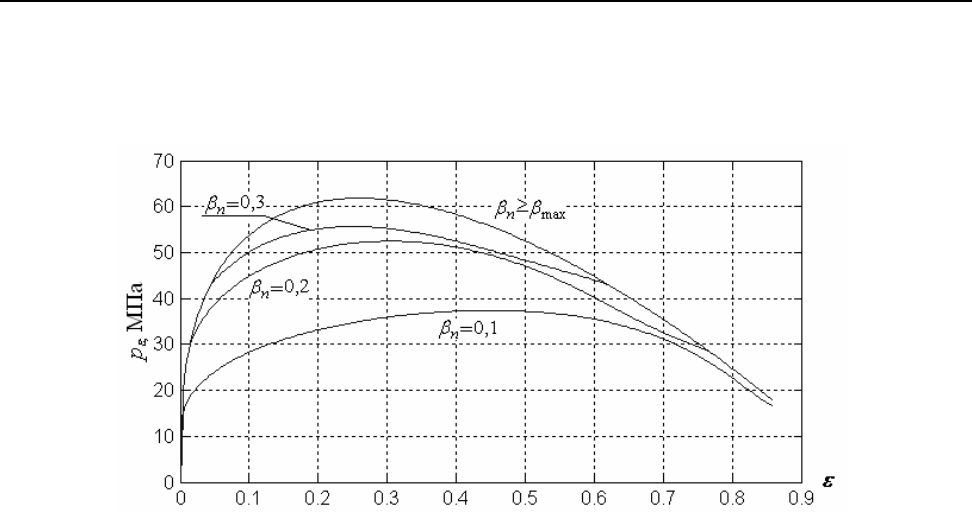
Рис. 2. Расчетные эпюры распределения контактного давления

p (МПа) в зависимо-

сти от относительного внедрения

ε и соответствующего значения коэффициента пропор-

циональности

β для марки стали 16ГС при температуре C°800 , в случае применения ножа

с относительной шириной режущей кромки

maxn

≥

(а),

0,2 (б), =β

0,1 (в).

Введем коэффициент

β относительной (к толщине H разрезаемого листа) ширины

контактной поверхности ножа. Применяя нож с

maxn

по мере относительного внедре-

ния ножей в металл будем иметь два варианта контакта (см. рис.1):

β≥β

– рассмотренный выше алгоритм полностью применим;

Обработка материалов давлением №1 (19), 2008

108

β<β

– вторая (удаленная от плоскости реза) вершина режущей кромки ножа

начнет внедряться в отрезаемую кромку, следовательно, изменится характер распределения

контактных давлений, что требует дополнения рассмотренного выше алгоритма.

Внедрение в отрезаемую кромку второй вершины приведет к росту контактных дав-

лений с этой стороны режущей кромки ножа, тогда как в вершине, расположенной в

плоско-

сти реза, и зоне, прилежащей к ней, существенных изменений происходить не будет. Распре-

деление контактных давлений в зоне, прилегающей ко второй вершине, является отображе-

нием распределения контактных давлений в зоне резки относительно нейтральной оси, коор-

дината положения которой может находиться в пределах:

−

≤

−

εε

. (8)

С учетом

y уравнение (2) примет следующий вид:

() ()

(

)

[

]

τε

β−+εετ+σ=

nn0maxT

yyykyp . (9)

Расчетное значение координаты нейтральной оси, с учетом свойств разрезаемого ма-

териала, определяется выражением:

(

)

(

)

max

nmax

min

nminn

ykyky += , (10)

где

k и

max

k – весовые коэффициенты, равные:

.1k,k

maxnmaxmaxnmin

−

β= (11)

min

y и

max

y – граничные значения координаты нейтральной оси:

()

(

)

[

]

min

21,0maxy β−ββ−β=

εε

, (12)

[]

εε

ββ−β=

max

1,0maxy

. (13)

На рисунке 2 для сравнения приведены расчетные эпюры распределения контактного

давления

p (МПа) в зависимости от относительного внедрения

и соответствующего зна-

чения коэффициента пропорциональности

для марки стали 16ГС при температуре

C800°

в случае различной относительной ширины режущей кромки

По результатам численной реализации представляется возможным получить зависи-

мость удельного сопротивления резанию при различных величинах

путем интегрирова-

ния уравнения (9):

()

∫

min

dyypp

, (14)

где

()

nmin

,0max β−β=β

– нижний предел интегрирования.

Расчетные зависимости кривых удельного сопротивления резанию (сталь 16ГС) от

глубины относительного внедрения для различных значений

при температуре C800°

приведены на рисунке 3.

Оценку эффективности применения ножей с уменьшенной относительной шириной ре-

жущей кромки можно получить, подсчитав удельную работу процесса резки при различных зна-

чениях

Обработка материалов давлением №1 (19), 2008

109

Как можно видеть из представленных зависимостей с уменьшением параметра

наблюдается снижение удельной работы резания

w , которое для 1,0=

при температуре

C°800

достигает

%3531K

Рис. 3. Расчетные зависимости кривых удельного сопротивления резанию (сталь

16ГС) от глубины относительного внедрения для различных значений

при температуре

C800° .

Выводы

На основе инженерных подходов разработана модель напряженного состояния кон-

тактной поверхности в процессе горячей резки. По результатам численной реализации полу-

чена зависимость удельной работы резания от относительной ширины режущей кромки но-

жа, что позволяет разработать рекомендации по расширению сортамента листов допускае-

мых к резке в горячем состоянии за счет

изменения конструкции ножа.

Результаты работы могут быть использованы при дальнейших исследованиях по рас-

ширению сортамента листов разрезаемых на дисковых ножницах в горячем состоянии.

ЛИТЕРАТУРА

1. Боровик П.В. Влияние конструкции ножа на величину работы в процессе резания металла на нож-

ницах / П.В. Боровик, В.А. Луценко // Сб. науч. тр. ДонГТУ. – Алчевск, 2007. - Выпуск 24. – С. 264-270.

2. Боровик П.В. Влияние конструкции ножа и технологических параметров процесса резания металла

ножницами на величину удельной работы / П.В. Боровик, В

.А. Луценко // Сб. науч. тр. ДонГТУ. – Алчевск, 2007.

- Выпуск 25. – С. 187-193.

3. Wisselink H.H. Analysis of Guillotining and Slitting, Finite Element Simulations // Ph.D-Thesis, University

of Twente, The Netherlands, January 2000.

4. Грудев А.П. Теория прокатки: Учебник для вузов. – М.: Металлургия, 1988. – 240 с.

5. Целиков А.И., Смирнов В.В. Прокатные станы. – М.: Металлургиздат, 1958. – 412 с.

6. Марочник сталей и сплавов / В.Г. Сорокин, А.В. Волосникова, С.А. Вяткин и др.;

Под общ. ред.

В.Г. Сорокина. – М.: Машиностроение, 1989. – 640 с.

Боровик П. В. – сотрудник ДонГТУ;

Луценко В. А. – д-р техн. наук, профессор ДонГТУ;

Ульяницкий В. Н. – д-р техн. наук, профессор ДонГТУ.

Дон ГТУ – Донбасский государственный технический университет, г. Алчевск.

lutsenko@dmmi.edu.ua

Обработка материалов давлением №1 (19), 2008

110

УДК 621.771.01: 621.771.8

Сатонин А.В.

Кулик Т.А.

Кулик Н.А.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ПЛАКИРОВАНИЯ

ОТНОСИТЕЛЬНО ТОНКИХ БИМЕТАЛЛИЧЕСКИХ КОМПОЗИЦИЙ

В последнее время все более широкое применение получают изделия из биметаллов,

являющихся не только заменителями дефицитных металлов, но и представляющими самостоя-

тельную группу промышленных материалов, необходимых при создании новых машин, при-

боров и различных изделий[1, 2]. Биметаллическими могут быть: листы, ленты, трубы и дру-

гие изделия, состоящие из двух, а иногда и

из трех слоев разнородных металлов, которые

обеспечивают более широкий комплекс необходимых потребительских свойств. В настоящее

время в мире производится более 50 видов биметаллов. Они востребованы в приборостроении,

в химической промышленности, в автомобилестроении и в инструментальном производстве.

Получают биметаллические материалы различными способами, при этом широкий класс ком-

позиций из пластичных металлов (малоуглеродистая

сталь, медь, алюминий, никель и их спла-

вы) можно получать высокопроизводительным способом плакирования прокаткой [1].

С точки зрения математического моделирования, по аналогии с традиционными про-

цессами прокатки монометаллических сред, в зависимости от соотношения длины дуги кон-

такта L и средней толщины

различают плакирование относительно толстых

(

0,3h/L

< ) и относительно тонких ( 0,3h/L

≥ ) композиций. В отличие от процессов

плакирования относительно толстых заготовок, которые характеризуются доминирующим

влиянием внешних зон и, как следствие, повышенной степенью неоднородности по высоте

сечений очага деформации, условия реализации процессов плакирования прокаткой относи-

тельно тонких лент, листов и полос сред характеризуются доминирующим влиянием сил

внешнего трения, а кинематическое и деформированное состояния

по высоте указанных се-

чений являются в этом случае близкими к однородному [3]. Отмеченное подтверждено ре-

зультатами целого ряда и теоретических, и экспериментальных исследований, в том числе и

результатами теоретических исследований, выполненных с использованием метода полей

линий скольжения [3]. Предположение об однородности кинематического состояния позво-

ляет применить гипотезу плоских сечений [4] и в качестве

модели использовать очаг дефор-

мации, разделенный по всей протяженности зоны пластического формоизменения на конеч-

ное множество выделенных элементарных объемов.

С учетом изложенного выше математическое моделирование напряженно-

деформированного состояния материала относительно тонкой двухслойной биметаллической

композиции при реализации процесса плакирования прокаткой было осуществлено на основе

численного рекуррентного решения конечно-разностной формы условий

статического рав-

новесия выделенного элементарного объема, полученного путем разбиения всей протяжен-

ности зоны пластического формоизменения на их конечное множество. Расчетная схема оча-

га деформации и выделенного элементарного объема, соответствующая самому общему слу-

чаю условий реализации процесса плакирования прокаткой двухслойной биметаллической

композиции, представлена на рисунке 1.

В качестве исходных данных в этом случае

использовали начальные значения толщин

нижней

h и верхней

h составляющих, конечную толщину всей композиции

h , радиусы

рабочих валков

R ,

R и окружные скорости их вращения

1в

V ,

2в

V , напряжения задних на-

тяжений, прикладываемых к нижней

и верхней

составляющим, интегральное, при-

веденное к единице ширины

значение переднего натяжения bТ

, коэффициенты, харак-

теризующие условия внешнего и межслойного трения, а также коэффициенты регрессии и

константы, необходимые для определения механических свойств материалов упруго-

деформируемых рабочих валков и упруго-пластически деформируемых составляющих про-

катываемой композиции.