Новикова С.С., Соловьев А.В. Социологические и психологические методы исследований в социальной работе

Подождите немного. Документ загружается.

Таблица 7

Данные о возрастном составе группы

Возрастная

группа

Частоты Проценты Накопленные

частоты

Накопленные

проценты

20-29 12 40,0 12 40,0

30-39 8 26,7 20 66,7

40-49 5 16,7 25 83,4

50-59 3 10,0 28 93,4

60-69 2 6,7 30 100,1

Всего 30 100,1 30 100,1

В первом столбце представлены возрастные интервалы. Обратим внимание, что

они не пересекаются, то есть мы берем интервалы 20-29, 30-39, а не 20-30, 30-40.

Иначе не ясно будет, куда относить индивидов, попадающих на стык возрастных

групп. Во втором и третьем столбцах представлены соответственно частоты и

проценты. Глядя на них, мы видим, что возрастной состав группы неоднородный: в

ней преобладают молодые люди, а люди старших возрастов встречаются реже.

В четвертом и пятом столбцах частоты и проценты представлены в несколько

иной форме, которая применима для упорядоченных категорий (шкал порядка или

отношений). Частоты и проценты суммируются по всем предыдущим категориям.

При такой форме представления данных хорошо видно, сколько человек или какая

доля выборки находятся ниже (или выше) определенного уровня. В нашем примере 25

человек из 30, или 83,4 %, моложе пятидесяти лет.

Данные о распределении переменной можно представить не только в форме

таблиц, но и в форме графиков, которые еще более наглядны. Рассмотрим четыре

типа графиков, которые чаще всего используются в случае одномерного

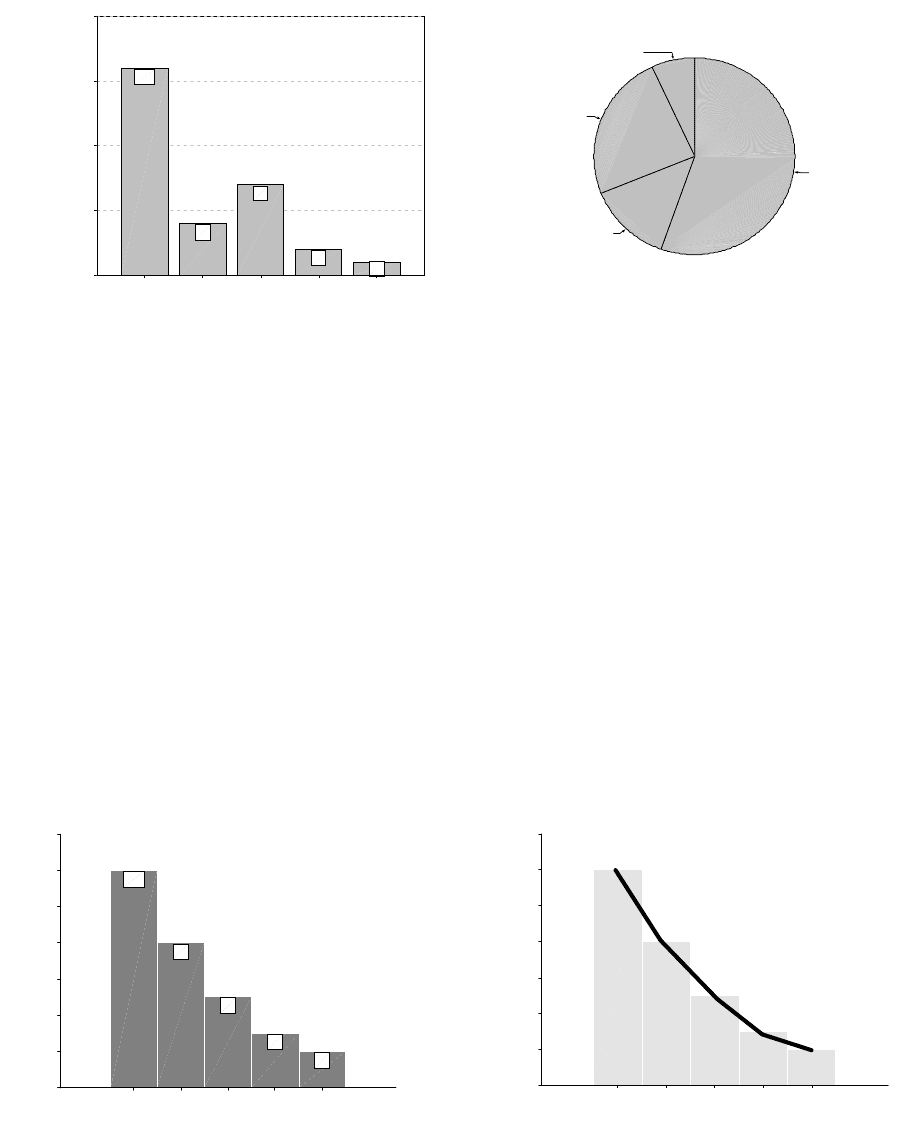
распределения. Для неупорядоченных категорий (шкала наименований) обычно

применяют столбиковые диаграммы. Число столбиков соответствует числу

категорий. Высота каждого столбика отражает частоту встречаемости данной

категории. Все столбики рисуются одинаковой ширины и не соприкасаются друг с

другом. Порядок их расположения на горизонтальной оси может быть любым. Для

представления долей и процентов удобны круговые диаграммы. Весь круг

соответствует единице или ста процентам, а величина каждого сектора отражает

представительство соответствующей категории.

331

Данные отсутствуют

Вдова/вдовец

Разведен/разведена

Холост/не замужем

Женат/замужем

Фиг. 1. Столбиковая диаграмма

(Данные взяты из табл. 1)

6.9%

24.1%

13.8%

55.2%

Вдова/вдовец

Разведен/разведена

Холост/не замужем

Женат/замужем

Фиг. 2. Круговая диаграмма

(Данные из табл. 1)

Для наглядного представления измеренных данных (шкала равных интервалов)

используются так называемые гистограммы и полигоны. Гистограмма похожа на

столбиковую диаграмму, только на горизонтальной оси в этом случае указываются

границы интервалов. Столбики примыкают друг к другу. Высота столбика

соответствует наблюдаемой частоте. Гистограмму легко преобразовать в полигон. Для

этого середины вершин каждого столбца соединяются между собой прямыми

отрезками. Получается ломаная линия, повторяющая контур, образуемый столбиками.

Гистограмма удобна для изображения особенностей одного распределения.

Преимущество полигона заключается в том, что на одном графике можно представить

несколько полигонов и затем сравнивать между собой разные выборки.

Возрастные группы

60-70

50-60

40-50

30-40

20-30

Фиг. 3. Гистограмма распределения

возрастов (данные из табл. 2)

Возрастные группы

Фиг. 4. Полигон распределения

возрастов (те же данные)

Построение таблиц и графиков – это первый шаг статистического анализа.

Следующим шагом является оценка параметров распределения. Вычисляются

показатели, которые позволяют дать еще более сжатое описание наблюдаемых

значений. Эти показатели распадаются на две основные группы: меры

центральной тенденции и меры рассеяния. К наиболее часто используемым

332

показателям первого типа относится так называемое (арифметическое) среднее.

Вычисляют его, как известно, путем суммирования значений всех наблюдений

и деления полученной суммы на общее число наблюдений. В случае

сгруппированных данных поступают следующим образом: находят середину

каждого интервала, это значение умножают на частоту, полученные величины

складывают и делят на общее число наблюдений. Рассматриваемый показатель

характеризует область распределения, в которой концентрируются наиболее

типичные представители изучаемой выборки. Но это справедливо лишь для тех

случаев, когда распределение близко к нормальному. При таком распределении

основная масса значений концентрируется в его средней части, а любые

отклонения встречаются тем реже, чем дальше они отстоят от центра.

Например, распределение такого признака, как рост человека, в целом близко к

нормальному: больше всего людей среднего роста, а очень высокие и очень

маленькие попадаются довольно редко. Средняя величина удобна для

сравнения двух выборок или двух популяций. Так, мы говорим, что мужчины в

среднем выше женщин, и это утверждение вполне справедливо, несмотря на то,

что встречаются высокие женщины, рост которых значительно превышает

среднестатистический. Или, например, известно, что средний рост мужчины-

пигмея меньше роста средней европейской женщины.

Две другие меры центральной тенденции – это мода и медиана. В качестве

моды берется значение, которое чаще всего встречается в распределении. Моду

специально вычислять не надо. Достаточно сгруппировать данные и выбрать

тот класс, в который попадает больше всего наблюдений. В разобранном выше

примере (см. табл. 6) лучше всего представлена категория семейных людей. Это

и есть мода для данной выборки. Можно рассчитать среднее количество детей в

современной российской семье. Допустим, мы получим показатель 1,3. Но

какой реальный смысл он будет иметь? Что такое три десятых ребенка?

Правильнее сказать, что сейчас в семье чаще всего один ребенок, то есть

использовать моду в качестве показателя центральной тенденции. Встречаются

распределения, имеющие не одну, а две моды. Распределение такого типа

называется бимодальным. На графике в этом случае мы увидим две вершины.

Чаще всего это указывает на то, что выборка является неоднородной: в ней

присутствуют два типа объектов. Констатация такого факта обычно наводит нас

на мысль разбить всю выборку на две подгруппы и рассмотреть их отдельно.

Для того чтобы найти медиану, нужно ранжировать все наблюдения, то

есть расположить их в порядке возрастания значений. Значение того

наблюдения, которое окажется как раз посредине, и будет медианой. А если

333

число наблюдений четное? Тогда сравнивают значения двух наблюдений,

попадающих в середину. Если они различаются между собой, то берется их

среднее арифметическое значение. В случае сгруппированных данных медиана

рассчитывается по специальной формуле. Когда распределение имеет

нормальный вид (то есть оно симметрично), его среднее арифметическое

значение и медиана совпадают. Когда же распределение асимметрично

(скошено), медиана лучше схватывает его центральную тенденцию.

Выбор подходящей меры центральной тенденции определяется как

характером распределения, так и характером используемых данных.

Качественные данные (шкала наименований) допускают использование только

моды. Для ранжированных данных (шкала порядка) допустимо использование и

моды, и медианы. Количественные данные (шкала равных интервалов) можно

описывать любым из трех показателей, хотя на практике чаще всего в этом

случае вычисляют среднее арифметическое значение. Именно этот показатель

вместе с показателем рассеяния участвует в расчете целого ряда других

статистических показателей.

Показатели рассеяния характеризуют степень разброса данных вокруг

некоторого среднего значения. Мы говорим о значительном рассеянии тогда,

когда многие значения сильно отклоняются от воображаемого центра

распределения. Специалисты по математической статистике говорят, что в этом

случае данные "размазаны". Про распределение, характеризующееся малым

разбросом, говорят, пользуясь аналогией из области стрельбы, что данные

ложатся кучно. Понятно, что во втором случае среднее значение оказывается

более информативным показателем, чем в первом случае, то есть оно лучше

описывает выборку в целом. Например, в кордебалет идет строгий отбор

танцовщиц по росту. В результате рассеяние показателей роста в этой группе

людей значительно меньше, чем по популяции в целом. Зная средний рост

балерины, можно быть уверенным, что реальный рост любой балерины будет

очень близок к нему. Если брать измерительные инструменты, то их точность

определяется степенью разброса получаемых с их помощью данных: чем

меньше разброс, тем выше точность измерения.

Как оценить степень рассеяния значений переменной? Здесь тоже

существуют разные способы, выбор которых в каждом конкретном случае

определяется характером данных – их типом и распределением. Некоторое

представление о рассеянии мы получаем, когда рассматриваем крайние члены

распределения. Расстояние между ними называется размахом. Например, в

разобранном выше примере (см. табл. 7) выборка включает индивидов, чей

334

возраст колеблется в пределах от двадцати до семидесяти лет. Общий размах

составляет пятьдесят лет. Большинство людей (40 %) моложе тридцати лет. Но

в выборку попали два человека, которым уже за шестьдесят. Если мы вычислим

показатель центральной тенденции по формуле среднего арифметического, то

получим значение 36,5. Так как распределение сильно скошено, этот показатель

сильно отличается от моды (25 лет). Медиана в этом случае лежит между этими

двумя значениями (33,3).

Для более точной оценки рассеяния в случае измерений по шкале равных

интервалов используется показатель, называемый дисперсия. В этом случае

учитывается отклонение каждого индивидуального значения от среднего в одну

или в другую сторону. Нас интересует сумма таких отклонений. Но в случае

симметричного распределения эта сумма всегда обращается в нуль, поскольку

положительные и отрицательные отклонения взаимно гасятся. Поэтому

используют сумму квадратов отклонений. Квадрат любого числа – величина

положительная, и эта сумма тем больше, чем больше рассеяние измерений.

Сумма квадратов отклонений от среднего, деленная на количество наблюдений

N дает значение дисперсии. Если извлечь из этого выражения квадратный

корень, то мы получим еще одну меру рассеяния – стандартное отклонение,

которое также называют среднеквадратическим отклонением. Удобство этого

показателя в том, что он выражается в тех же единицах, что и сами измеренные

величины.

Рассмотренный показатель очень удобен, когда форма распределения

близка к той, которая называется нормальным распределением. Мы уже

упоминали этот термин. Сейчас поясним, что он означает. Нормальное

распределение – это такое распределение непрерывного признака, которое

симметрично относительно среднего значения, и если откладывать его значения

на графике, то кривая имеет вид колокола. Рост человека оказывается одним из

признаков, обнаруживающих распределение, хорошо описываемое нормальной

кривой. Если мы измеряем рост многих людей, например – призывников в

армию, а затем на основе этих данных строим график, то мы получаем

нормальную кривую. С точки зрения анализа данных нормальное

распределение привлекательно тем, что его можно исчерпывающе описать

через два параметра – значение среднего и стандартного отклонения

(дисперсии). Вместо тысяч значений – всего два числа! Чрезвычайно

эффективный метод сжатия информации.

Стандартное отклонение действительно позволяет четко задавать критерии

для выявления статистической нормы. Это возможно благодаря тому, что

335

свойства нормального распределения хорошо известны и достаточно просто

описываются. Так, известно, что в диапазоне одного стандартного отклонения в

обе стороны от среднего оказывается примерно 68% всех наблюдений, а если

взять два стандартных отклонения, то этот участок распределения покроет

около 95% всех случаев. Значит, за этот диапазон выходит всего 5% возможных

наблюдений. Проинтерпретируем это содержательно. Что значит "высокий

человек"? С точки зрения статистики, человек, рост которого превышает

средний рост по данной популяции более чем на величину одного стандартного

отклонения, может считаться высоким, а того, чей рост выделяется в

положительную сторону более чем на два стандартных отклонения, следует

отнести к категории очень высоких. Ведь такой рост будет встречаться не чаще,

чем в трех случаях из ста.

Используя свойства нормального распределения, можно ввести строгие

количественные критерии, определяющие, что такое "нормальный вес",

"нормальная острота зрения" и т.д. Психологические тесты тоже создаются с

опорой на эти статистические закономерности. Выше, в разделе о тестах, мы

касались процедуры конструирования и стандартизации тестов. Мы там

указывали, что нормы для оценки результатов испытаний выводят эмпирически

с использованием аппарата математической статистики. Теперь, после

знакомства с основными идеями статистического анализа, можно пояснить эту

процедуру. Трудность заданий подбирается таким образом, чтобы

распределение результатов решения тестовых задач (число правильных

ответов) описывалось нормальным законом. А затем строится шкала, где

среднему значению соответствует сто баллов, а стандартное отклонение равно

пятнадцати баллам. Выводимый показатель называется коэффициентом

интеллектуального развития (по-английски – intelligence quotient, или

сокращенно IQ). Человек, у которого этот показатель ниже 70, считается

умственно отсталым, а человека с показателем выше 130 относят к категории

особо умственно одаренных.

Мы подробно разобрали случай, когда анализируется характер

распределения одной переменной. Эти приемы очень важны, поскольку на них

основаны все другие виды статистического анализа. Теперь мы можем перейти

к более сложному виду анализа, каким является двумерный анализ. Здесь

рассматривается связь между двумя переменными. Мы имеем пары

наблюдений, полученные на одном объекте. Это могут быть, например,

результаты по двум тестам. Нас интересует, как один изучаемый признак связан

с другим.

336

Важнейшей мерой связи является коэффициент корреляции. Само слово

"корреляция" как раз и означает "взаимосвязь". Какого типа отношения

возможны между двумя переменными? Ну, во-первых, признаки могут быть

совершенно независимыми друг от друга, тогда изменения одного никак не

связаны с изменением другого. Мы говорим, что переменные не коррелированы

между собой. Если признаки связаны, то сама связь может быть прямой или

обратной. В первом случае большим значениям одного признака соответствуют

более высокие значения другого и наоборот. Во втором случае увеличение

первого признака сопровождается уменьшением второго, а уменьшение первого

– увеличением второго. Статистики говорят о положительной и отрицательной

корреляции. Наконец, степень связи тоже может варьироваться от максимума,

когда значения одного признака позволяют уверенно предсказывать значения

другого, до ее полного отсутствия. Коэффициент корреляции отражает всю

гамму возможных отношений. Его значение может варьироваться от +1 до -1.

Положительные значения указывают на прямую связь между переменными,

отрицательные – на обратную. Нуль соответствует случаю отсутствия корреляции.

Предположим, что у многих людей измеряют рост и вес тела. Каждый

человек описывается двумя показателями, и в результате образуются два ряда

измерений. Сравнивая между собой пары измерений, мы стремимся выявить

характер связи между переменными. Между ростом и весом тела существует

довольно высокая положительная корреляция. Это значит, что высокий человек,

как правило, весит больше, чем человек меньшего роста. Связь эта не

однозначная: высокий человек может быть очень худым, а человек невысокого

роста может быть очень полным, поэтому значение коэффициента корреляции в

данном случае находится где-то между 0 и +1, видимо, чуть ближе к единице.

Коэффициент корреляции по-разному вычисляется для измеренных

показателей (рост, вес) и для ранжированных данных (оценки, предпочтения),

но его окончательная форма и интерпретация остаются теми же. Если данные

носят качественный характер (мужчина – женщина, совершеннолетний –

несовершеннолетний, работающий – пенсионер), то вместо коэффициента

корреляции применяются другие меры связи, основанные на сравнении частот.

Для тех случаев, когда два ряда получены с помощью разных шкал, имеются

свои вычислительные процедуры, но общая логика анализа сохраняется.

Следует специально остановиться на вопросе интерпретации данных

двумерного анализа, поскольку здесь требуется известная осторожность. Мы

касались этой проблемы в первой главе, когда обсуждали момент перехода от

научного описания к объяснению. Там отмечалось, что сам факт наличия связи

337

между двумя переменными еще не позволяет утверждать о существовании

причинно-следственных отношений между ними. Корреляция может указывать

на такие отношения, но одной этой информации недостаточно, чтобы делать

однозначные выводы. Тогда мы пояснили это на примере интерпретации

уровня интеллекта родителей и детей. Сейчас имеет смысл вернуться к данной

проблеме и рассмотреть ее глубже.

Итак, в ряде случаев корреляция между двумя переменными отражает то

обстоятельство, что они связаны между собой как причина и следствие. Но

причинно-следственные отношения – это лишь один из возможных типов связи.

Определенно можно утверждать только следующее: если два явления никак не

связаны между собой, то заведомо исключены любые взаимовлияния.

Отсутствие корреляции опровергает гипотезу о возможных связях причинно-

следственного характера, и такой отрицательный результат может быть полезен

в плане уточнения теории.

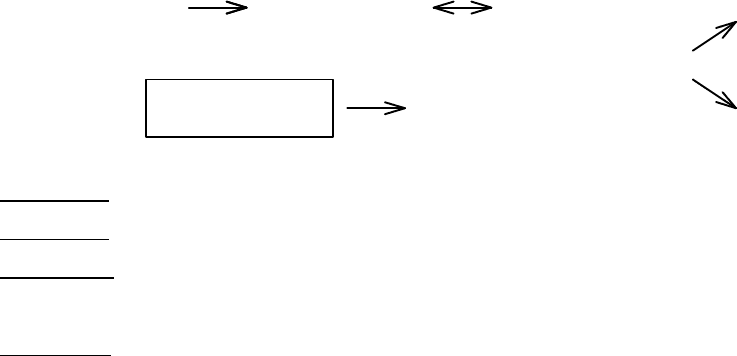
Отношения между двумя коррелированными переменными X и Y могут

быть содержательно самыми разными:

Случай 1: явление Х вызывает явление Y, выступает как его причина.

Случай 2: явления Х и Y взаимно обусловливают друг друга.

Случай 3: некоторое третье явление А вызывает явление Х и явление Y,

выступает как причина их обоих.

Случай 4: явление Х вызывает явление Y, действуя в комплексе с другими

факторами.

Для иллюстрации приведем пример. Он похож на шутку, но хорошо

демонстрирует суть проблемы. Если сравнивать между собой два показателя –

потребление мороженого и количество утонувших, то между ними можно

обнаружить положительную корреляцию. Значит ли это, что любовь к

мороженому приводит к несчастным случаям на воде или (совершенно

абсурдный вывод) что отношение здесь обратное? Конечно, нет. Очевидно, что

есть некий третий фактор, который объясняет оба явления. Это – температура

воздуха. В жаркую погоду едят много мороженого и купаются. В холодную

погоду потребление мороженого и количество купающихся резко падает.

A B C...X

338

Понятно, что в эти дни почти никто не тонет. Перед нами ситуация,

соответствующая третьему из схематически представленных случаев.

Социальные науки чаще всего имеют дело с явлениями, которые

отличаются множественной детерминацией и контекстуальным характером.

Здесь трудно устранить влияние посторонних переменных, выделить явление в

чистом виде. Поэтому необходима особая тщательность в интерпретации

наблюдаемых фактов. Для того чтобы избежать необоснованных выводов,

исследователь должен обладать определенной методологической культурой,

понимать, какого рода подводные камни могут встретиться на этом пути.

Корреляционный анализ представляет собой метод выявления связи между

двумя переменными. Если число переменных больше двух, то можно, вообще

говоря, рассматривать каждую пару отдельно. Но существуют приемы,

специально разработанные для данных такого рода, которые в совокупности

носят название многомерный анализ. Мы кратко рассмотрим один из этих

методов – факторный анализ, который довольно часто используется в

социальных исследованиях. В вычислительном плане он весьма сложен, но

использование компьютера существенно упрощает дело. Современному

исследователю не надо вдаваться в тонкости вычислительной процедуры, а

достаточно понимать возможности этого метода и знать особенности работы с

ним.

Факторный анализ является своеобразным развитием метода

множественных корреляций. Вначале рассчитываются коэффициенты

корреляции между парами переменных. Затем чисто математически получают

несколько общих факторов, связанных с группами изучаемых признаков.

Поскольку число таких факторов меньше числа исходных переменных, этот вид

анализа можно рассматривать как способ сжатия информации, приведения ее к

более компактному виду. Последний этап анализа – содержательная

интерпретация полученных факторов. Ее осуществляет сам исследователь,

выявляя те переменные (признаки), которые теснее всего связаны с каждым

фактором. Например, исследуются интересы людей. Если вокруг одного

фактора группируются такие виды активности, как посещение театра,

концертов, художественных выставок, то мы назовем такой фактор

"эстетические интересы". Другим фактором может быть, например, интерес к

спорту. В результате мы получаем несколько групп однотипных интересов. С

точки зрения структуры данных, отдельный фактор представляет собой как бы

интегральный индикатор, выявляющий комплекс взаимосвязанных проявлений.

Еще один пример. Исследование качества обслуживания в доме престарелых

339

путем опроса его обитателей выявило два главных фактора удовлетворенности:

отношение персонала (доброта, отзывчивость, уважение, готовность помочь,

расторопность) и условия содержания (состояние здания и территории,

оборудование комнат, чистота, качество питания).

Итак, факторный анализ является объективным методом выявления

структуры изучаемых данных. Его можно рассматривать как количественный

аналог типологического анализа, проводимого на качественном уровне. Будучи

формальным аппаратом, факторный анализ не может гарантировать, что

получаемые результаты будут интересными с точки зрения исследователя.

Например, иногда выделяемые факторы трудно содержательно

интерпретировать: в них входят довольно разнородные компоненты, которые

трудно объединить каким-то общим понятием. Во всяком случае, как любой

метод вообще, факторный анализ сам по себе не может быть хорошим или

плохим, эффективным или бесполезным. Все зависит от того, насколько

уместно он применяется, в какой степени он соответствует задачам

исследования и характеру анализируемых данных.

Теперь обратимся ко второй большой группе количественных методов

анализа, на основе которых делается статистический вывод. В этом случае

стоит задача перехода от отдельной выборки к характеристикам (параметрам)

генеральной совокупности, то есть всего класса объектов в целом. Дело в том,

что исследователь редко имеет возможность изучать всех представителей

какой-то группы или социальной категории. Можно, например, обследовать все

многодетные семьи, проживающие в данном микрорайоне, но тогда выводы в

полной мере будут относиться лишь к этой конкретной группе людей.

Насколько они справедливы для многодетных семей всего города или области?

Чтобы ответить на этот вопрос, нужно знать, насколько типична или

специфична обследованная группа. Если она типична, то сходные проблемы

выявятся и у других многодетных семей. Если группа очень специфична, то мы

не имеем права обобщать полученные данные. На языке статистики это значит,

что наша выборка принадлежит к другой генеральной совокупности. Опять мы

сталкиваемся с задачей сравнения характеристик выборки и генеральной

совокупности, с необходимостью суждения об их тождестве или различии.

В реальной практике исследования вопрос чаще всего ставится несколько

иначе, но логически он относится к тому же классу. Требуется сравнить две

группы (выборки) и решить, насколько значимо они различаются между собой.

Любой эксперимент предполагает оценку эффекта изучаемого воздействия.

Исследователь в этом случае стремится показать, что экспериментальная

340