Носов Г.В., Макенова Н.А., Канев Ф.Ю. Компьютерное исследование длинных линий и электромагнитного поля
Подождите немного. Документ загружается.


11
ал точки А может быть определен как работа, совершаемая силами по
переносу единичного положительного заряда (
q = 1 Kл) из точки А в
точку поля 0, потенциал которой принят равным нулю
0
,
A
A
Edl
причем этот интеграл определяется только положением точек
А, О и не
зависит от траектории, по которой происходило перемещение этого за-
ряда из А в О. Размерность
– вольт (В).
Таким образом, электростатическое поле является потенциаль-
ным
и безвихревым полем, т. к. линейный интеграл от напряженности
E
, взятый вдоль любого замкнутого пути, равен нулю, т. е.:
0
Edl или rot 0.
E
Если поле создается несколькими зарядами
12
,,...
n
qq q в пространстве с
ε
a
const , то его потенциал равен алгебраической сумме потенциалов
от каждого заряда в отдельности (метод наложения):
12
... .
n
Графически электростатическое поле в линейной среде изображается
совокупностью взаимно перпендикулярных линий напряженности и эк-
випотенциальных линий.
Линия напряженности (силовая линия) – это линия, в каждой точке
которой вектор
E
направлен по касательной. Силовые линии имеют на-
правление и они начинаются на положительно заряженном теле, а за-
канчиваются на отрицательно заряженном теле. Силовые линии пер-
пендикулярны к поверхностям проводников и поверхности земли.
Эк-
випотенциальная
линия или линия равного потенциала – это линия, в
каждой точке которой потенциал постоянен. Разность потенциалов ме-
жду этими линиями принимается одинаковым. Силовые линии при по-
строении картины поля проводятся перпендикулярно к линиям равного
потенциала так, чтобы, например, для плоскопараллельного поля полу-
чились квадратные ячейки между соседними силовыми и эквипотенци-
альными линиями.
Напряженность и потенциал связаны
между собой уравнением
grad ,
E
причем для потенциала справедливы уравнения Лапласа и Пуассона со-
ответственно
22
0, / ,
a

12
где
2
div(grad )
лапласиан,
3
Кл
м
– объемная плотность заря-
дов.
В каждой точке проводника потенциал одинаков, а на границе двух
диэлектриков потенциал непрерывен. На границе двух диэлектриков
равны касательные составляющие напряженности поля.
В электротехнических расчетах кроме вектора
E
используют также
вектор электрической индукции или вектор электрического смещения
,
a
DE
для которого справедлива теорема Гаусса
qSdD
s
или div .
D
Вектор
D
перпендикулярен поверхности проводника и равен по-
верхностной плотности свободного заряда на этом проводнике, а на
границе двух диэлектриков равны нормальные составляющие векторов
D
при отсутствии свободных зарядов на этой границе.
Характеристиками электростатического поля являются емкость и
энергия. Под
емкостью С между двумя телами, на которых имеются
равные и противоположные по знаку заряды
q, понимают отношение
абсолютной величины заряда на одном из тел к напряжению между те-
лами:
12
,
q
q
C
U
причем размерность емкости – фарада
(Ф).
Энергия, запасенная в объеме V электростатического поля, равна
2
,
2
a
э
V
E
WdV
где Е – модуль вектора напряженности.
Если электростатическое поле создается системой n заряженных
тел, имеющих потенциалы
1
,...,
n
и заряды
1
,...,
n
qq, то его энергия
может быть рассчитана как
1
1
.
2
n
экк
к
Wq
Под заряженной осью понимают весьма тонкий бесконечно длинный
металлический проводник с линейной плотностью заряда
,
Кл/м.

13
Электростатическое поле такой оси характеризуется:
;ln,
22
aa
E
rK
r
где r – расстояние от оси, K – постоянная.
Для электростатического поля двух параллельных разноименно
заряженных осей при помощи метода наложения можно определить
потенциал точки, расположенной на расстоянии
1
r от оси с зарядом
и на расстоянии
2
r от оси с зарядом
:
2
1
ln ,
2
a
r
r
причем линией нулевого потенциала будет линия с
2
1
1.
r
r
Если заряженная ось
расположена над проводящей плоскостью
(землей) и параллельна ей, то для расчета поля в диэлектрике, находя-
щемся выше границы раздела, применим метод зеркальных изображе-
ний, когда напротив заряженной оси относительно поверхности на том
же расстоянии помещается такая же диэлектрическая среда и фиктивная
заряженная ось с противоположным по знаку зарядом
. Далее мето-
дом наложения рассчитываются напряженность и потенциал над этой
плоскостью.
Если несколько параллельных заряженных осей с зарядами
123
, , ...
расположены над проводящей поверхностью и параллельно
ей, то для расчета поля в верхней полуплоскости применяются методы
зеркальных изображений (каждой оси) и наложения.
Если радиусы проводов линии значительно меньше расстояний
между проводами и расстояний до земли, то электрическое поле такой
линии будет соответствовать полю заряженных осей.
Электрическое поле многопроводной линии, расположенной па
-
раллельно поверхности земли является плоскопараллельным. Плоскопа-
раллельным называется поле, потенциал и напряженность которого не
зависят от одной из координат декартовой системы (например, z). Кар-
тина плоскопараллельного поля многопроводной линии, т. е. совокуп-
ность линий равного потенциала и линий напряженности, повторяется
во всех плоскостях сечений, перпендикулярных проводам (оси z). Таким
образом,
потенциал и напряженность электростатического поля много-
проводной линии зависят от двух координат x и y.
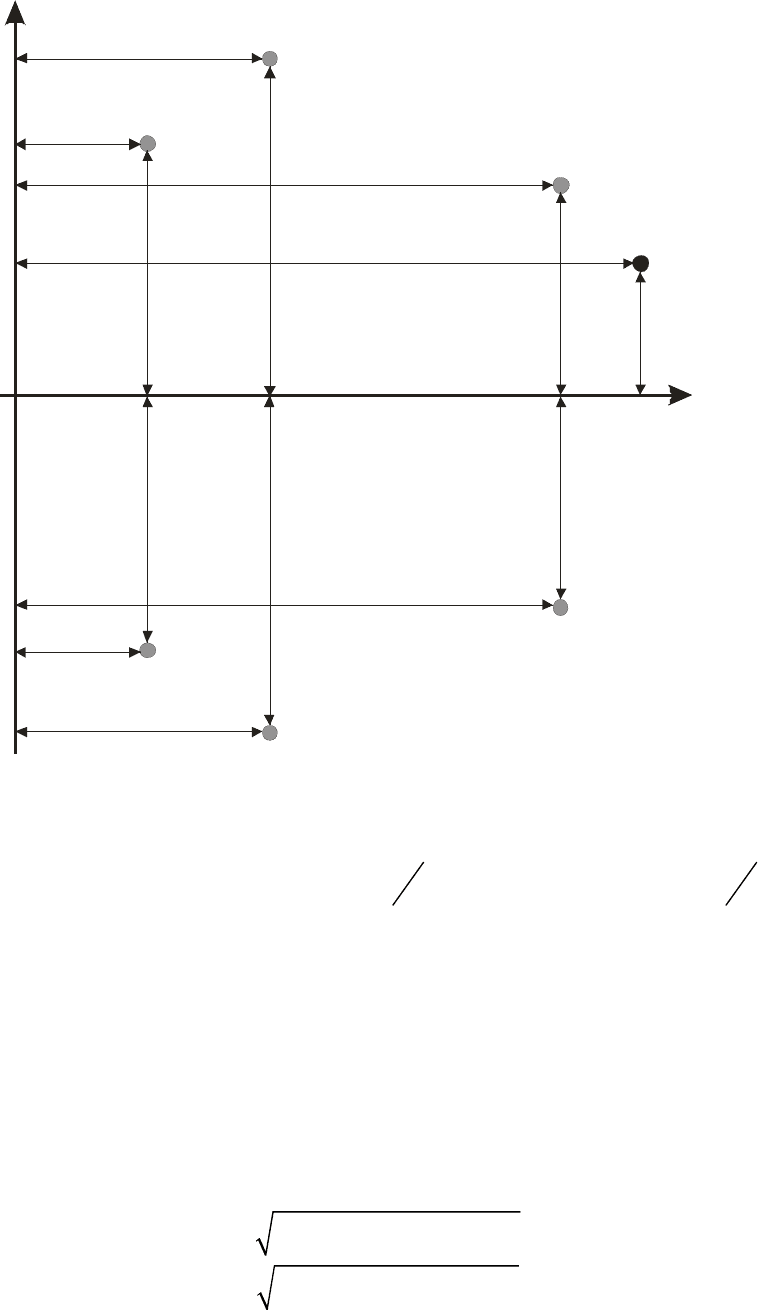
Пусть задана трехпроводная линия, расположенная над поверхно-
стью земли в воздухе с
0
a
(рис. 2.2).
14
N(x,y)
x
1
y
1
τ
3
τ
2
τ
1
x
2
x
3
x
y
2
y
3
y
y
3
y
2
y
1
−τ
1
−τ
2
−τ
3
0
x
1
x
3
x
2
X
Y
Рис.2.2. Трехпроводная линия и ее зеркальное изображение
Для линейных сред
0
Ф
,
м
ar
где
12
0
Ф
8,86 10
м
диэлектрическая проницаемость вакуума,
r
– относительная диэлек-
трическая проницаемость среды (для вакуума и воздуха
1).
r
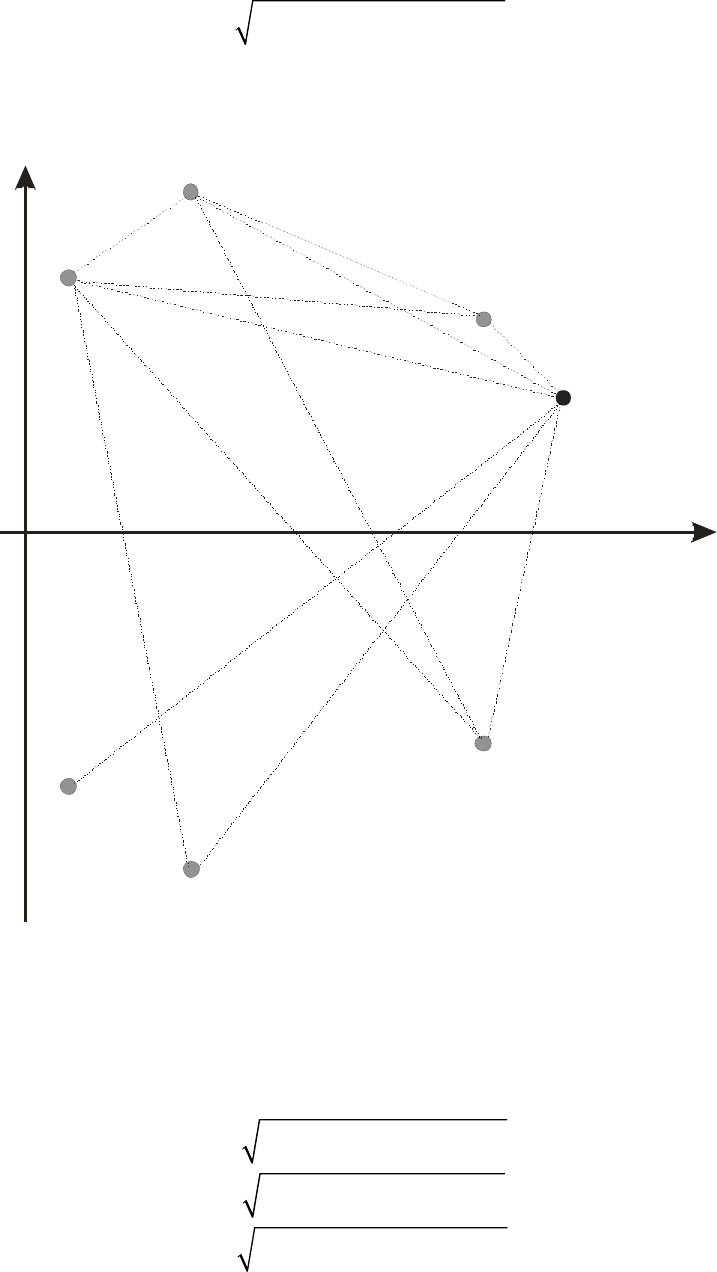
Гео-
метрические размеры трехпроводной линии представлены на рис. 2.3.
Здесь радиус проводов R много меньше расстояний
12 13 23
,,ddd и
123
,,yy y
. Линейные плотности заряда проводов составляют
123
,,
, а
потенциалы проводов
123
,,.
Если координаты проводов
12 3
,,
x
xx и
123
,,yy yзаданы (см.
рис. 2.2), то тогда расстояния между проводами будут следующими:
22
12 1 2 1 2
()(),dxxyy
22
13 1 3 1 3
()( ),dxxyy
15
22
23 2 3 2 3
()( ).dxxyy
N(x,y)
d
23
d
12
d
13
r
1
(1)
τ
3
τ
2
τ
1
D
23
D
13
D
12
−τ
1
−τ
2
−τ
3
r
1
(2)
r
1
(3)
r
2
(1)
r
2
(2)
r
2
(3)
0
X
Y
Рис.2.3. Геометрические размеры трехпроводной линии
Расстояния между проводами и их зеркальными изображениями будут
равны:
22
12 1 2 1 2
()( ),Dxxyy
22
13 1 3 1 3
()( ),Dxxyy
22
23 2 3 2 3
()( ).Dxxyy

16
На основании методов зеркальных изображений и наложения можно
получить уравнения (первая группа формул Максвелла), связывающие
потенциалы и заряды проводов:
1111122133
,
2211222233
,
3311322333
,
(2.11)
где
1
11
0
12
ln ,
2
y
R
2
22
0
12
ln ,
2
y
R
3
33
0
2
1
ln
2
y
R
–
собственные потенциальные коэффициенты (м/Ф) и
12
12 21
012
1
ln ,
2
D
d
13
13 31
013
1
ln ,
2
D
d
23
23 32
023
1
ln
2
D
d
– взаимные потенциальные коэффициенты (м/Ф).
Решая систему (2.1) относительно зарядов
123
,,
и полагая по-
тенциалы и потенциальные коэффициенты известными, получаем вто-
рую группу формул Максвелла
1111122133
,
2211222233
,
3311322333
,
(2.12)
где
11 12 13
21 22 23
31 32 33
– определитель системы (2.11),
2
22 33 23
11
,
2
11 33 13
22
,
2
11 22 12
33
– положительные собственные емкостные коэффициенты (Ф/м);

17
31 23 21 33
12 21
,
21 32 31 22
13 31
,
31 12 11 32
23 32
– взаимные емкостные коэффициенты (Ф/м), которые всегда отрица-
тельны.
Систему (2.2) можно переписать в виде третьей группы формул
Максвелла
1 11 1 12 1 2 13 1 3
()()
CC C ,
22121 2222323
() ()
CCC
,
33131 3232 333
()( )
CC C,
(2.13)
где
11 11 12 13
,
C
22 22 21 23
,
C
33 33 31 32
C
– собственные частичные емкости
(Ф/м);
12 21 12
,
CC
13 31 13
,
CC
23 32 23
CC
– взаимные частичные емкости
(Ф/м).
Энергия электростатического поля на единицу длины, создаваемо-
го тремя проводами, может быть рассчитана следующим образом:
11 2 2 3 3
1
().
2
э
W
(2.14)
В свою очередь, согласно методу наложения, потенциал в некото-
рой точке
N электростатического поля будет создаваться каждым заря-
женным проводом и его зеркальным изображением (рис. 2.2):
(1) (2) (3)
3
12
22 2
(1) (2) (3)
11 1
ln ln ln
22 2
а aa
rr r
rr r
,
(2.15)
где
,)()(
)(
2
1
2
1
1
1
yyxxr
,)()(
)(
2
2
2
2
2
1
yyxxr
2
3
2
3
3
1
)()(
)(
yyxxr
18
– расстояния от точки N до заряженных поводов 1, 2, 3 соответственно;
,)()(
)(
2
1
2
1
1
2
yyxxr
2
3
2
3
3
2
2
2
2
2
2
2
)()(
,)()(
)(
)(
yyxxr
yyxxr
– расстояния от точки
N до зеркальных изображений проводов 1, 2, 3
соответственно;
x, y – координаты точки N.
Расчетные формулы (2.11)–(2.15) будут справедливы для однопро-
водной
23
(0)
и двухпроводной
3
(0)
линий.
Так для однопроводной линии имеем
1111
,
11111111
11
1
,
C
11
1
(),
2
э
W
(1)
1
2
(1)
1
ln
2
а
r
r
,
(2.16)
а для двухпроводной линии получаем
1111122
,
2211222
,
1111122
,
2211222
,
11111212
(),
CC
22121 222
() ,
CC
11 2 2
1
()
2
э
W ,
(1) ( 2)
12
22
(1) ( 2)
11
ln ln .
22
а a
rr
rr
(2.17)
Если потенциалы проводов
123
,,
и геометрические размеры
12312 3
,, ,,, ,
R
xx x yy yзаданы, то по вышеприведенным формулам мож-
19
но рассчитать потенциальные и емкостные коэффициенты, частичные
емкости, линейные плотности зарядов проводов
123
,,
, запасаемую
полем энергию
э
W . Меняя координаты x, y точки N, можно найти рас-
пределение потенциалов в электростатическом поле, на основании ко-
торого построить линии равного потенциала и перпендикулярно к ним
силовые линии. В результате получаем картину электростатического
поля многопроводной линии.
§2.2.Потенциальные, емкостные коэффициенты и частичные
емкости. Группы формул Максвелла
Если несколько проводов линии находятся в среде с неизменной
диэлектрической проницаемостью, то связь между их линейными плот-
ностями зарядов
(Кл/м) и потенциалами
(В) выражается линейны-
ми зависимостями – тремя группами формул Максвелла. Применитель-
но к трехпроводной линии при потенциале земли равном нулю, каждая
из этих групп представляет систему трех уравнений.
Уравнения с потенциальными коэффициентами
ij
:
1111122133
2211222233
3311322333
,
,
.
(2.21)
Здесь
ii
– собственный потенциальный коэффициент i-ro провода,
ij
–
взаимный потенциальный коэффициент i-го и j-го проводов.
Уравнения с емкостными коэффициентами
ij
:
1111122133
2211222233
3311322333
,
,
.
(2.22)
Уравнения с частичными емкостями
ij
C :
11111212 1313
22121 2222323
33131 3232 333
()(),
() (),
()( ) .
CC C
CCC
CC C
(2.23)
Как видно из уравнения (2.1), для определения собственного по-
тенциального коэффициента
ii
нужно измерить потенциал и заряд i-ro
провода при отсутствии зарядов на других проводах. Например:
20
23
1
11
1
0
.
(2.24)
Для определения взаимного потенциального коэффициента нужно
в тех же условиях измерить заряд i-го и потенциал j-го проводов:
23
2
21
1
0
.
(2.25)
причем в силу принципа взаимности
21 12
.
Для определения собственного емкостного коэффициента
ii
изме-
ряется значения потенциала и заряда i-ого провода, когда остальные за-
землены, а для определения взаимных коэффициентов
ij ji
в тех же
условиях измеряется заряд i-гo и потенциал j-го провода.
23
1
11
1
0
,
(2.26)
23
2
21
1
0
.
(2.27)
Наконец, собственную частичную емкость
ii
C можно определить,
как следует из уравнения (2.3) при равенстве потенциалов всех трех
проводов (четвертый, как всегда заземлен), измерив этот потенциал и
заряд i-й провода. Например,
123
1
11
1
C
.
(2.28)
Если в условиях этого опыта рассмотреть первое уравнение сис-
темы (2.22), то получим соотношение
1
11 12 13 11
1
C .
(2.29)
Если же сравнить вторые уравнения систем (2.22) и (2.23) при
23
0
, то окажется что
21 21
C . В общем случае для системы N
проводов справедливы соотношения:
1
,
N
ij ij ii ij
j
CC.
(2.10)
При этом показание амперметра пропорционально зарядам
i
, а показа-
ние вольтметров равно потенциалам проводов
i
(потенциал 4 провода
равен нулю).
