Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

Nanoelectronic-Based Detection for Biology and Medicine 81.2 Interfacing Biological Molecules 1435

acterization tools to quantify or qualify the quality

of the surface chemistries or the quantity of im-

mobilized DNA. This is understandable, ﬁrst due

to the complexity of the DNA molecule (that in-

creases even with the addition of a single base);

secondly the interactions of the surface chemical prop-

erties can greatly change the binding quality of the

molecules, which may cause more of the nonspe-

ciﬁc adsorption; and thirdly because of the mechanical

and chemical ﬂexibility (or instability) of DNA, e.g.,

hybridization, conformational changes, effect of am-

bient and temperature, its sensitivity to biologically

signiﬁcant entities, and even to slight changes in chem-

ical composition of the buffer. Notwithstanding the

challenges in driving DNA, the highest degree of

selectivity due to complementarity of bases makes

it a molecule of choice in a large variety of self-

and mediated-assembly experiments and biosensor

applications.

A lot of experiments use physical adsorption to

immobilize DNA on a variety of devices. Some ap-

proaches use deposition of DNA from a buffer solution

using catalysts such as MgCl

for better DNA adhe-

sion to metal electrodes [81.3]. A receding meniscus of

a drying droplet has also been shown towards immo-

bilizing 16μm long DNA on microstructured surfaces

(Fig.81.1) [81.2]. Imaging techniques such as atomic

force microscopy (AFM) are done to conﬁrm the pres-

ence of DNA before doing electrical measurements.

Passive adsorption of DNA has also been shown in 96-

well polystyrene plates by incubation of the molecules

with cationic reagents [81.4]. In a similar fashion,

a high-frequency electric ﬁeld has also been used to trap

DNA and proteins between the electrode gaps [81.5].

Under the inﬂuence of DEP,theDNA is known to

be stretched into a long, thin conﬁguration, i.e., it is

not randomly coiled. Fluorescence imaging is used to

prove the presence of the DNA in the gaps between the

electrodes.

By far, chemical adsorption and immobilization is

considered the most stable, reliable, and reproducible

method to attach biological molecules onto substrates

and nanodevices. Usually, the molecules are modiﬁed

with a functional group(s) that has a high covalent

afﬁnity to the surface. Most common and well-studied

functional pairs are thiol–Au, biotin–(strept)avidin, and

the his–tag system. The complementarity of the DNA

strands is also employed extensively, where single-

strand (ssDNA) is attached to the surface (called the

probe), and complementary ssDNA is supplied from

solution (the target).

1µm

b)a)

1µm10 µm

Fig. 81.1 DNA positioned in electrode gaps of 2 μm. Fluores-

cence imaging shows Au electrodes structures dark and the DNA

bright. Arrows mark electrode gaps. Reprinted with permission

Gold–thiol is a favorite chemistry of choice for

a lot of applications and has been employed in a num-

ber of studies to immobilize DNA for conductivity

measurements, hybridization detection, sequence detec-

tion, DNA-templatedself-assembly, etc.[81.6–9]. Glass

slides and lately thermally oxidized silicon surfaces are

also routinely used to immobilize DNA through var-

ious silane-, aldehyde-, and amine-modiﬁed schemes.

Probe DNA molecules are accordingly modiﬁed at the

appropriate end(s). The functionalized surfaces exhibit

various surface energies (wettability) and/or electrical

charges. DNA is chemically anchored on substrate sur-

face either directly to a chemical layer like silane or

through a hetero/homobifunctional moiety. Figure 81.2

depicts an example of amine-modiﬁed-DNAattachment

chemistry through a silane layer on a SiO

surface. The

attachment of the biological entities has been character-

ized in various labeled or unlabeled ways, e.g., a recent

review has summarized various methods and strategies

that have been developed to detect nucleic acids with

electrical means [81.10], or, direct optical detection of

DNA hybridization on the surface of a charge-coupled

device [81.11]. Chemical attachment of DNA has been

investigated on various surfaces such as carbon, alu-

minum, indium-tin oxide, SiO

,Si

, and most of all,

glass slides [81.7,12].

SAMs of biological molecules have also been used

to make reliable contacts. The networks of polyse-

quences of DNA (DNA with the same base repeated)

have been shown to self-assembled onto a mica surface.

Poly(dG)–poly(dC) DNA networks showed a uni-

form reticulated structure and poly(dA)–poly(dT) DNA

formed a cross-linked network [81.13]. DNA has also

been shown to aid the construction of functional cir-

Part H 81.2

1436 Part H Automation in Medical and Healthcare Systems

HO–SI–CH

–CH

–O–CH

–CH–CH

O–SI–CH

–CH

–O–CH

–CH–CH

Substrate

SiO

-layer

O–SI–CH

–CH

–O–CH

–CH–CH

–NH

–CH

–CH–CH

–O–P–O–OLIGO

Base

OH O

N–CH

–CH–CH

–O–P–O–OLIGO

Fig. 81.2 Schematic depicting chemical bonds in attaching 3



-amino-modiﬁed DNA to a thin SiO

ﬁlm. Attachment

occurs by secondary amine formation between an epoxysilane monolayer and the 3



-amino linkage. From [81.11], by

permission of Oxford University Press

cuits, by constructing Ag wires using the self-assembly

of a λ-DNA as a template [81.14]. The λ-DNA was

uncoiled and stretched to contact two Au electrodes.

The Ag

ions were deposited along the DNA, through

/Na

ion exchange asAg

formed complexes with

the DNA bases, resulting in nanometer-sized metallic

Ag aggregates bound to the DNA skeleton. In a simi-

lar approach, DNA-templated assembly of Ag clusters

has been shown with electrochemical detection [81.8].

The Ag cations were electrostatically collected along

the gold-surface-tethered DNA duplex. The Ag aggre-

gates were dissolved and the potentiometric stripping

of the dissolved Ag was detected on a thick-ﬁlm carbon

electrode.

81.2.1 Guidelines for Preparing Silicon

Chips for Biofunctionalization

DNA is immobilized by physical or chemical adsorp-

tion, the latter being more robust and stable in a variety

of ambient conditions. A number of chemistries have

been shown by various researchers for attachment of

DNA via chemical bonds. The motivation for such at-

tachments has been wide, ranging from biosensors to

integrated circuits; for the detection of chemical or bio-

logical species in biosensors; to controlled assembly of

nanodevices and structures in nanoelectronics and bio-

physical studies.

The general scheme of DNA attachment is through

surface functionalization of the substrate and the mod-

iﬁcation of DNA with a linker end-terminus, as shown

in Fig.81.3. The linker end-terminus can then bind to

a hetero/homobifunctional molecule, or the chemical

structure of the linker itself is exploited to react with

surface functionalized moieties due to certain binding

afﬁnities. The bifunctional molecules have at least two

available chemically reactive positions, one of which

attaches to the surface-grafted molecular layer and the

other to the end-linker of the DNA.

Homobifunctional cross-linkers have two identical

reactive groups thus can be used in a one-step chemical

cross-linking procedure. DNA modiﬁed with various

end groups or even without end groups has been shown

to attach to certain functional groups. Attachment of

ssDNA to the surface molecular SAM is mostly veriﬁed

Surface

functionalization

Linker

Si/SiO

/Au/Mica/Glass/...

Fig. 81.3 General schematic of DNA attachment via linker

molecule

Part H 81.2

Nanoelectronic-Based Detection for Biology and Medicine 81.2 Interfacing Biological Molecules 1437

SiO

Fig. 81.4 Hydroxylation of SiO

surface (after [81.15], by

permission of Oxford University Press)

with the ﬂuorescently labeled complementary ssDNA

that hybridizes with the adsorbed ssDNA.Otherde-

tection schemes involve radioactive dyes such as

phosphor imaging, and chemiluminescence. We present

two protocols that can be adapted for covalent attach-

ment ofamine-modiﬁed DNA to SiO

surfaces (adapted

from [81.15,16]).

For direct DNA attachment to the chips, vari-

ous silanizing agents have been pursued and reported

to functionalize SiO

surfaces. Generally, the silane-

containing chemicals have a tendency to react with

hydroxyl groups at the surface of the chips, resulting

in silanol groups. The hydroxyl group density at the

surface of the SiO

thus inﬂuences the self-assembly

of the silane layer and ultimately the number of at-

tached DNA. The hydroxyl groups on the surface of

Si/SiO

chips are generally achieved by piranha solu-

tion (H

, in various proportions) treatment

of the SiO

surface, or O

plasma etch treatment. Fol-

lowing these treatments, the OH-rich surface of SiO

looks as shown in Fig.81.4.

Exposing the OH-rich surface to a silane results in

the reaction of Si of the silanizing chemical with the

O group, thus releasing the hydrogen. To directly attach

the DNA molecules, an amine modiﬁcation at theend of

DNA canbe utilized.The reactive site of the silane (e.g.,

an epoxide) makes a covalent bond with the amine. The

surface coverage of immobilized ssDNA can be veriﬁed

by using complementary ssDNA tagged with ﬂuores-

cence. All chip surface processing should be done in

a controlled environment, e.g. a glovebox to minimize

exposure to ambient moisture and contamination.

For better surface coverage, a homobifunctional

linker can be used ontop ofthe surfacesilane. Thechips

can be silanized using 3-aminopropyltrimethoxysilane

(APTMS), and 1,4-phenylene diisothiocyanate (PDITC)

can be used as a homobifunctional agent. Again

APTMS hydrolyzes the OH-rich SiO

surface thus

strongly attached through covalent bonds to it, creating

a SAM of amino silane anchors. The amine group at

the other end of the APTMS covalently attaches with

the C of one of the isothiocyanate groups of the PDITC

cross-linker. PDITC has two isothiocyanate sites where

its C can react with the NH

–ofAPTMS. The

other isothiocyanate site on PDITC provides amino-

reactive terminus for probe DNA attachment. These

PDITC-activated chips are thus immersed in the amine-

modiﬁed DNA, completing the attachment chemistry

for the NH

-oligo attachment on the SiO

surface. The

unreacted sites of PDITC are then deactivated by N–N

diisopropylethylamine exposure.

81.2.2 Veriﬁcation of Surface Densities

of Functional Layers

The functionalized surfaces can be characterized for

adsorbed layers by ellipsometry and contact-angle mea-

surements. The silane layer thickness can be measured

by ellipsometry. An isotropic value of n = 1.50 for

the silane layer and n = 3.858−0.018i for the silicon

substrate refractive index can be used. The values for

monolayers range between 1.45–1.50 in the literature,

but this range would give an error of less than 1Å

during measurements. The monolayer thickness can be

accurately measured up to ±2Å. A number of read-

ings should be taken at different places on the chips and

compared with control chips.

The hydrophilicity/hydrophobicity of a surface is

usually expressed in terms of wettability. Hydrophilicity

and hydrophobicity are general terms used to describe

relative afﬁnity of materials for water (hydrogen bond-

ing). Hydrophilicity of a surface is a measure of its

strong afﬁnity to the water as the polar surfaces form an

H bond with water. The opposite hydrophobic surfaces

have aversion to water. Contact-angle measurements

with deionized water can show functionalized chips to

be less hydrophilic than control chips with only SiO

and no chemical treatment. The OH-rich surfaces of

control chips can make more H bonds with the wa-

ter and so would be hydrophilic, whereas in relative

terms the chemically treated chips would have fewer

OH-groups left on the surface and so would be less hy-

drophilic and can be termed as becoming hydrophobic.

A nice example of highly hydrophobic surface is fresh

Si surface with no native oxide. Si resists being wet-

ted by water, thus the water forms drops with contact

angles ≥75

◦

Part H 81.2

1438 Part H Automation in Medical and Healthcare Systems

81.3 Electrical Characterization of DNA Molecules on Surfaces

In this section we will review studies on charge trans-

fer and direct measurements of electrical conduction

through DNA, along with the various charge transport

mechanisms that have been proposed and simulated.

It has been established that a number of factors and

conditions contribute to the behavior of DNA conduc-

tivity [81.17, 18]; the number of base pairs (bp), the

sequence and length of DNA [81.3], changes in the dis-

tance and angle between bases, the inﬂuence of water

and counterions, humidity, contact chemistry, surface

smoothness, electronic contamination, ambient condi-

tions, temperature, and buffer solution components.The

double-helix structure of DNA depends on the hy-

drophobicity of the bases. The hydrophobic bases turn

towards the center, away from the water. The presence

of the condensed cations counters the negative charges

of the phosphate backbone. The water molecules and

cations are thus an integral part of the overall pic-

ture and exert nonnegligible forces on the base-pair

stack [81.19]. All these factors dictate that DNA is a dy-

namic and very complex system to simulate owing to

its structural, chemical, environmental, and vibrational

properties.

81.3.1 Indirect Measurements

of Charge Transfer Through DNA

The idea of DNA being electrically conductive can

be traced back as far as 1962, when Eley and Spivey

hinted at efﬁcient charge transfer through DNA as

...aDNA molecule might behave as a one-dimensional

aromatic crystal and show a π-electron conductivity

down the axis. They proposed that the DNA structure

was ideal for electron/hole transfer proceeding along

a one-dimensional pathway constituted by the overlap

between π-orbitals in neighboring base pairs [81.20].

At 400K, they reported conductivities on the order of

−12

(Ω cm)

−1

andenergygaps(ΔE) of about 2.42±

0.05eV. While emphasizing lack of knowledge on the

ribonucleic acid (RNA) structure at that time, they re-

ported a similar experimental value for RNA. Snart,

in 1973, reported a similar and reproducible value of

the energy gap (2.4eV) that was affected by ultraviolet

(UV) irradiation [81.21]. Snart’s measurement method

was very similar to the one employed by Eley and

Spivey. These can be considered as the starting points

of the quest for DNA conductivity.

In the early 1990s, Barton and co-workers per-

formed experiments that suggested long-range electron

transfer in DNA [81.22]. The donor and acceptor

molecules were intercalated on the DNA strands. When

the donor was photoexcited, the ﬂuorescence of the

donor was quenched due to electron transfer to ac-

ceptor. These results showed very rapid transfer of

carriers over > 40Å via π-stacked base pairs. However

other researchers disputed these results, as reproduction

of the results with other acceptor and donor candi-

dates was found to be problematic. The starting point

of the controversy came the very next year when,

in similar experiments, Brun and Harriman used or-

ganic donors and acceptors [81.23] and concluded that

charge transfer rates drop off quickly with increasing

length of the DNA. Ly et al. studied the mechanism

and distance dependence of radical anion and cation

migration and suggested that the structural ﬂexibility

of DNA dictates mixed behavior of hole-hopping and

continuous orbital mechanism [81.24]. Such a mech-

anism in which the injection of charge disturbs the

molecular structure is called a phonon-assisted polaron-

like hopping mechanism. Such a disturbance in DNA

most likely results in the reduction of intrabase dis-

tance and unwinding of DNA, giving way to increased

π-electron overlap and shift of internal charges in-

side H bonds. Giese and Wessely, in 2000, veriﬁed

these two mechanisms experimentally [81.25]. They re-

ported a coherent superexchange reaction (single-step

tunneling) and a thermally induced hopping pro-

cess for long-range charge transfer, slightly inﬂuenced

by the number of intercalated adenine–thymine (AT )

bases. Generally, in a hopping mechanism, the gua-

nine (G) base is considered the most favorable for

landing of holes or trapping, basically because it has

the least ionization potential among the four bases:

G < A < cytosine (C) < T, independent of nearest-

neighbor effects. Since then, more experimental and

theoretical research has resulted in seemingly contra-

dictory results.

81.3.2 Direct Measurement

of DNA Conduction

and DNA Conductivity Models

The sensing of DNA has been a direct result of the elec-

trical characterization studies. DNA has been shown to

have metallic-like conductivity[81.26], semiconducting

behavior [81.27], and also as an insulator [81.28].

Fink and Schonenberger used gold-coated perfo-

rated carbon foil as a sample holder to make DNA

Part H 81.3

Nanoelectronic-Based Detection for Biology and Medicine 81.3 Electrical Characterization of DNA Molecules on Surfaces 1439

networks, spanning the holes atop the carbon foil.

A low-energy electron point source (LEEPS) was used

to image the sample, while a conductive tip contact

was placed at the middle of the bundle. They reported

an upper value of DNA resistivity of 1 mΩ cm, mea-

sured through 600–900nm-long bundles of λ-DNA in

vacuum, concluding that DNA was a good conducting

molecular wire [81.26]. Dekker and co-workers re-

ported semiconducting behavior of DNA, by measuring

the conductivity of 10.4nm long poly-DNA, elec-

trostatically trapped between two 8 nm spaced metal

electrodes, as shown in Fig.81.5 [81.27]. The ﬁrst-

principles calculations for carrier transport through

DNA, as well as experiments performed on 40nm to

15μm long λ-DNA suggested exponential decay in

conductance with the DNA length [81.28]. In these ex-

periments, electrodes were formed by sputtering gold

onto a mica substrate with DNA already immobilized

on the surface. Refuting the high conductivity reported

by Fink and Schonenberger, similar experiments were

carried out and the high conductivity was explained

to be an artifact due to electronic contamination from

LEEPS. The very next year, these results were chal-

lenged by Kasumov et al. by their experiments on DNA

deposited between 0.5μm apart rhenium/carbon (Re/C)

electrodes [81.29]. The Re/C contacts had supercon-

ducting properties. Again, DNA was reported to behave

8nm

–6 –4 –2 0 2 4

Current (nA)

Voltage (V)

–1

–2

DNA

–+

SiN

SiO

Fig. 81.5 I–V curves measured at room temperature on

a DNA molecule trapped between two metal nanoelec-

trodes. Reprinted by permission from Macmillan Publish-

ers Ltd: Nature [81.27], copyright (2000)

like a metallic conductor. It was suggested that DNA

had proximity-induced superconductivity properties at

low temperature. It was suggested that the compres-

sion caused on the DNA structure due to deposition on

surface would change its electronic behavior [81.30].

Simultaneous measurement of the height and conduc-

tivity of λ-DNA ﬁlm formed on mica showed that

DNA did not conduct when its height was 1 nm. When

the mica surface was functionalized with pentylamine

ﬁlm before DNA deposition, its height was seen to

be around 2nm, and it was conductive. The reduced

mica–DNA interaction due to the pentylamine layer

ensured that the structure and conductivity was unaf-

fected. Yoo et al. measured the conductance through

poly-DNA and reported semiconducting behavior with

little effect of ambient conditions or vacuum [81.31].

Storm et al. reported DNA to be an insulator, as op-

posed to the previous report of the semiconducting

behavior from the same group [81.3]. It was concluded

that DNA was insulating at length scales longer than

40nm and that bare DNA had limited use as a con-

ducting molecular wire [81.32]. The effects of oxygen

adsorption on the poly-DNA conductance have also

been explored [81.33]. The oxygen content was shown

to modulate the resistance. It was also reported that

poly(dG)–poly(dC) DNA was a p-type semiconductor

and poly(dA)–poly(dT) DNA was an n-type semicon-

ductor. De Pablo and co-workers reported a different

approach ofcontactless setup (to avoidpossible artifacts

caused by the contacts) to investigate DNA electrical

properties [81.34]. They reported that the dielectric con-

stant of DNA was similar to that of mica. This study

provided a qualitative result of DNA being as insulating

as mica.

A scanning tunneling microscope (STM) tip has

also been used to study DNA molecules [81.35]. The

STM tip was used to contact the Au electrode in 3 μM

thiol-modiﬁed dsDNA solution.

Individual molecular junctions were created by

moving the tip out of contact with the ﬂat gold electrode

with DNA molecules bridging the distance between the

tip and the substrate. The conductance showed a series

of steps. For 8bp dsDNA, the conductance histogram

showed peaks at near-integer multiples of a fundamen-

tal conductance value, 1.3×10

−3

or ≈0.1μS, where

= 2e

/h ≈77μS. The conductance was also seen

to be inversely proportional to the length of (GC)

se-

quences (for 8bp or longer DNA). The insertion of

AT b p decreased the conductance with a decay con-

stant of 0.43Å

−1

. Qualitative differences between the

conductivity of ssDNA and dsDNA are also reported,

Part H 81.3

1440 Part H Automation in Medical and Healthcare Systems

ssDNA being insulating over a 4eV range between

±2V, and dsDNA being like a wide-bandgap semicon-

ductor [81.36]. Iqbal et al. investigated the effects of

the DNA sequence on its conductivity [81.37]. They

chemically anchored thiol-modiﬁed DNA between gold

nanogaps. It was seen that the conductivity through the

DNA molecule increased with increasing GC content.

Such behavior could be attributed to the increased hole

hopping between the hydrogen bonds in the guanine–

cytosine pair [81.38]. As the ionization potential of

guanine is the lowest (G < A < C < T), this would pro-

vide the easiest path for the conduction of holes[81.30].

Moreover, the triple hydrogen bonds between the G and

C bases as compared withthe double hydrogen bonds in

the A and T bases putatively result in more paths for the

charge ﬂow in higher-GC-content sequences [81.38].

This results in less resistance to the charge ﬂow in the

sequence containing more G–C pairs and results in de-

crease in resistance between various GC-rich sequences

by an order of magnitude. They also showed the pos-

sibility of using DNA as a reversible fuse, blowing off

at high temperature and turning back on when a con-

ducive environment became available. This was seen by

temperature cycling of their devices. Such a framework

could also be used as an electrical DNA hybridization

sensor. In another report, Mahapatro et al. showed that

the DNA conductivity scaled with the surface density

of chemically immobilized DNA [81.39]. The surface

density of the DNA was seen to be higher with high salt

concentrations, resulting from better screening of the

DNA phosphate backbone charges and reduced electro-

static repulsion. They observed that the conductivity of

DNA molecules decreased exponentially as the number

of adjacent AT pairs wereincreased, replacing GC pairs.

This also showed that the GC pairs provide a more con-

ductive path to the charge transfer. These ﬁnding can

have consequences in DNA-based molecular electron-

ics and direct label-free detection of DNA sequence and

hybridization.

While the experimentalists have been debating the

behavior of DNA, a number of theoretical models have

been proposed for the DNA conductivity mechanisms.

Almost all the proposed transport ideas rely on the

experimental results, and can be broadly categorized

as either model simulations or ab initio calculations.

The wide variety of these models is understandable

due to the large number of variables that affect the

conducting properties of DNA. Jortner and co-workers

suggested two distinct DNA charge transport mecha-

nisms in 1998 [81.40]. They proposed that transport

occurs either by the direct unistep hole tunneling from

one base pair to another, or by a multistep charge

transport through the base pairs, exhibiting a weak de-

pendence on the separation distance between the donor

and the acceptor. They further proposed that the charge

transport mechanism was determined by the speci-

ﬁcity of the intercalating base sequences, which they

called bridge. Yu and Song modeled DNA as a one-

dimensional (1-D) disordered system with electron

transport occurring between localizedstates as variable-

range hopping [81.41]. These localized states in the

sequence would present the candidate landing sites for

a hopping electron, while such localization would be

enhanced by structural changes in DNA with temper-

ature. They deﬁned a crossover temperature above or

below which transport would be either simple nearest

neighbor thermal hopping or the carrier would hop dif-

ferent ranges, respectively. Such variable-range hopping

mechanism is somehow consistent with the two pos-

sible mechanisms proposed by Jortner et al. and Ly

et al. [81.24, 40]. Yi modeled the dsDNA molecule as

a two-legged charge ladder to render the presence or ab-

sence of conductance gaps seen in I–V plots of GC-rich

and GC-poor sequences, respectively [81.42]. The gap

in conduction plots was explained with strong Coulomb

repulsion with eV values much larger than thermal en-

ergy. This repulsion is encountered with a screening

effect of the cations in the solution. This is a classi-

cal example of ab initio calculation. Various reports

describing electronic properties of DNA have been pub-

lished, delving into the coupling strengths between

bases, the highest occupied molecular orbital (HOMO)

and lowest unoccupied molecular orbital (LUMO)val-

ues and energies, band structures of various dsDNA,

effect of doping (speciﬁcally, O

doping) on conduc-

tance, structural effects on conduction, etc. The random

and stochasticprocesses in the complexDNA–electrode

system have been identiﬁed, explaining the wide claims

over values of DNA conductivity (metal, semiconduct-

ing, and insulator) [81.43]. As many as 12 parameters

have been simulated in adjusting HOMO and LUMO

bands in such systems.

Most of the theoretical models assume coherent

tunneling to be a major mechanism, with a length (L)-

dependent rate of charge transfer R [81.30]

R ∝exp(−βL) ,

(81.1)

where β is the tunneling decay length, the larger β

is, the faster the rate of tunneling decreases with in-

creasing distance. There have been various, sometimes

contradictory, values reported for β [81.44, 45]. Berlin

et al. found β to be 0.1Å

−1

for sequential tunneling

Part H 81.3

Nanoelectronic-Based Detection for Biology and Medicine 81.4 Nanopore Sensors for Characterization of Single DNA Molecules 1441

and about 1 Å

−1

for coherent tunneling by quantitative

analysis using kinetic rate equations [81.46].

The mechanisms proposed in the theoretical mod-

els may or may not occur in a system altogether, but

there is higher probability for presence ofmore than one

mechanism in any given experiment. The ideal model

should take care of the effects of DNA structure, ther-

mal motion of charges as described by classical models,

effects of cations in the solution on the structure and

on the Coulomb charging, temperature, intermolecular

and intramolecular attractions and repulsions, effect of

contacting conductors and the chemistries used to con-

tact the DNA, etc. Almost all studies consider charge

transport and conductivity on the path along the DNA

length. Little, if any work has been done, until lately,

on charge transport in the direction perpendicular to

the axis of the DNA backbone. Zwolak and Di Ventra

described unique signatures of each base due to their

differing electronic and chemical structures [81.47].

They considered a system of electrodes through which

a ssDNA passes such that at any given time only one

base interacts with the electrodes. Such a system can

be visualized as a nanopore made with a very thin

membrane, with electrodes on the very edges. With

electrode–electrode spacing of 15 Å, they found the ra-

tio of current of A (I

) and the current of other bases

)tobeI

=20, 40, and 660 for X =G, C, and

T, respectively. This difference in ratios is postulated to

stem from relative positions of the Fermi level with re-

spect to HOMO and LUMO, and the density of states

at Fermi level. The effects of nearest neighbor were

also calculated, with T found to be the most sensitive

to such effects. These ﬁndings are very interesting as

they can be used in conjunction with nanopore mea-

surements of DNA translocation, as will be explained

in next section.

81.4 Nanopore Sensors for Characterization of Single DNA Molecules

Biological entities, such as cells, proteins, and DNA,

carry charges, and can be forced to move by an electric

ﬁeld in a buffer solution, a phenomenon called elec-

trophoresis. Electrophoresis is usually applied in a gel

or capillary to separate biological entities based on their

size and charge. Electrophoresis in gel and capillaries

has given rise to the idea of characterization by a sin-

gle pore through which charged entities can be driven.

Therefore, characterizations of biological entities by

a single pore are actually an analogous application of

gel and capillary electrophoresis. The basic design of

a nanopore characterization setup consists of two com-

partments, ﬁlled with saline buffer solution, separated

by a membrane with the pore, with an anode and a cath-

ode set in each compartment; the pore provides the only

path for ionic currents and the electrophoretic move-

ment of DNA or other biological species of interest.

When DNA moves electrophoretically from the cath-

ode to the anode, it traverses the pore. As it does so,

the ionic current is altered and most typically decreases

due to pore blockade. When DNA has passed through

the pore, the current recovers to its original level. The

characteristics of DNA can possibly be determinedfrom

these current ﬂuctuations.

81.4.1 Biological Nanopores

Kasianowicz et al. pioneered the use of a single

2.6nm diameter α-hemolysin (α-HL) channel [81.48].

α-HL is a protein toxin from the bacterial species

Staphylococcus aureus. A solvent-free bilayer mem-

brane of diphytanoyl phosphatidylcholine (an artiﬁcial

lipid bilayer membrane) was formed across a ≈0.1mm

diameter oriﬁce. The oriﬁce was in Teﬂon partition

separating two buffer-ﬁlled compartments. When α-HL

was added to the compartment, it reconstituted into the

lipid bilayer, making a channel. A single channel usu-

ally formed within 5min. They used these channels

for current ﬂuctuation detection when a single DNA

traversed and passed through the pore. The transloca-

tion times, or the pulse widths, were proportional to

the DNA lengths. A patch clamp ampliﬁer was used

to convert current to voltage. In the absence of DNA,

applying a potential of −120mV resulted in ionic cur-

rents free of pulses. Following the addition of DNA to

the cis side of the protein pore, numerous short-lived

current blockades occurred (the current was reduced

by 85–100%). The blockades lasted from several hun-

dred to several thousand microseconds, depending on

the polymer length. For a given polymer length, the to-

tal number of pulses was seento be directly proportional

to polymer molar concentration. It was further shown

that DNA length, one of the DNA characteristics, was

directly proportional to the mean lifetime of the peaks

in the signals. This realized determination of lengths of

individual RNA or DNA chains using single-channel

measurements. Applying the same principle towards

a chemical sensor, Bayley and co-workers detected or-

Part H 81.4

1442 Part H Automation in Medical and Healthcare Systems

ganic molecules of relative molecular mass as low as

100 using α-HL pores [81.49]. The innovative step in

their study was to equip the α-HL nanopore with an in-

ternal, noncovalently bonded molecular adapter which

mediated channel blocking by the analyte, thus sensi-

tizing the nanopore to speciﬁc organic and chemical

species. The work showed that β-cyclodextrin (βCD)

molecule was sensitive to different guest molecules,

as shown in Fig.81.6. Thus, when bound to βCD,

members ofthe adamantanefamily ofpetroleum deriva-

tives could be distinguished, as could the members of

the group of tricyclic pharmaceuticals that included

imipramine and promethazine. These guest molecules

made their presence known by altering the electrical

conductivityof the α-HL pore.A singlesensing element

of thissort couldbe usedto analyzea mixtureof organic

molecules with different binding characteristics, so that

the pore could be in a way programmed for range of

sensing functions.

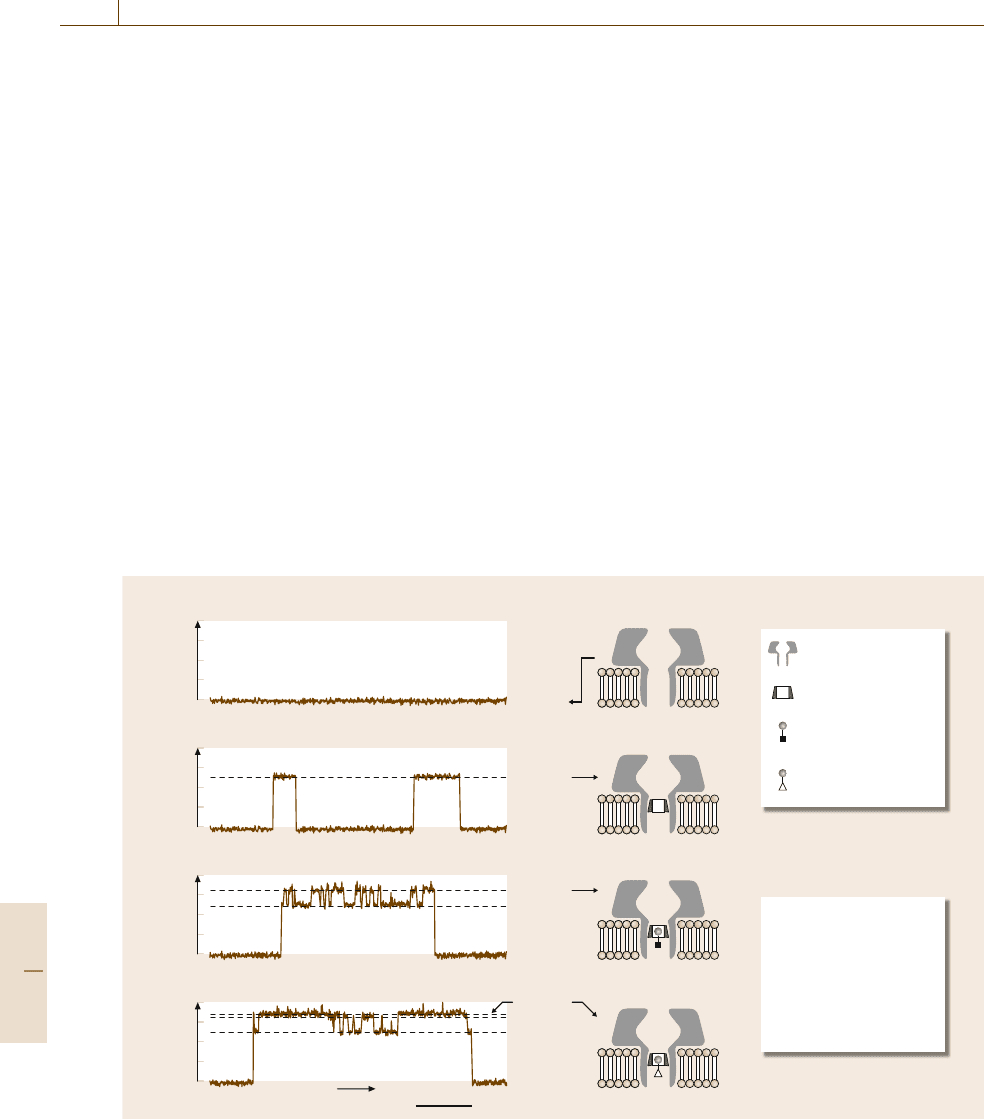
Meller et al., extending on the work of Gu et al.,

used the statistical data derived from the patterns of

events to show that nucleotides of different sequences

trans

cis

trans

cis

trans

cis

trans

cis

20ms

Time

α-HL

β-CD

2-adamantanamine

hydrochloride (A

)

Level 1

α-HL

Level 2 α-HL•βCD

Level 3 α-HL•βCD•A

Level 4 α-HL•βCD•A

1-adamantane

carboxylic acid (A

)

a) I (pA)

–15

–30

Level 1

Level 2

b) I (pA)

–15

–30

Level 1

c) I (pA)

–15

–30

Level 1

d) I (pA)

–15

–30

Level 2

Level 3

Level 4

Level 3

Fig. 81.6a–d Bilayer recordings at −40mV showing the interaction of a single α-HL pore with βCD and the analytes

2-adamantanamine (A

) and 1-adamantane carboxylic acid (A

). Reprinted by permission from Macmillan Publishers

could be distinguished from each other [81.50]. Six

polymers with the same length but different sequences

were measured. Difference between the translocation

duration and the temporal dispersion of transloca-

tion duration were used to then distinguish between

poly(dA)

100

and poly(dC)

100

DNA. The translocation

times varied among the polymers even if they had

the equal lengths, thus different sequences could be

discriminated in a mixture. Above 50

◦

C, the struc-

ture of the pore was not stable and measurements

could not be performed. In another study, Bayley and

co-workers covalently attached ssDNA within the lu-

men of the modiﬁed α-HL pores to form a DNA

nanopore [81.51]. The ssDNA molecule was attached

on the cis side of the α-HL channel, resulting in du-

plex formation with complementary sequences in the

internal cavity. The binding of ssDNA molecules to

the tethered DNA strand caused changes in the ionic

current ﬂowing through the α-HL nanopore. The DNA

nanopores were able to discriminate between individual

DNA strands up to 30 nucleotides in length differing

by a single base. The mean event lifetimes were ob-

Part H 81.4

Nanoelectronic-Based Detection for Biology and Medicine 81.4 Nanopore Sensors for Characterization of Single DNA Molecules 1443

trans

cis

dCMP

M113R

αHL

βCD

Fig. 81.7 Schematic depicting the α-HL pore, the met-113

substituted with Arg (blue), am

βCD,andthe2



-deoxy-

cytidine 5



-monophosphate molecule (dCMP). Adapted

Chemical Society

tained by lifetime histogram analysis and it was seen

that the type of mismatched base pair inﬂuenced the

lifetime, and that the mismatch had the most dramatic

effect when it was positioned in the middle of the

oligonucleotide. Using an array of DNA tethered α-HL

pores they sequenced a complete codon in an individ-

ual DNA strand. They did not look into any change

in the translocation time of a DNA sequence com-

plementary to the tethered DNA as compared with

the translocation of the same through an untethered

pore. In another report, Bayley and co-workers reported

another engineered α-HL pore approach to detect indi-

vidual nucleoside monophosphates (Fig.81.7) [81.52].

The nucleoside monophosphates are individual bases of

DNA (A, G, C or T) with a single phosphate group.

The nucleoside monophosphates, like DNA, are also

negatively charged thus traverse the pore under the

trans-channel bias [81.53]. The α-HL pores were mod-

iﬁed with amino-cyclodextrin am

βCD as adapter and

its positive charges altered the translocation time for the

nucleosides. They attained accuracy as high as 98% (for

G) using this approach.

81.4.2 Solid-State Nanopore

Researchers have been making point contacts since as

far back as 1977. These were used mainly for material

science studies, especially ballistic transport experi-

ments. The schematics of these structures were very

much like nanopores, as these stand today, but the aim

was quite different [81.54, 55]. The design of current

solid-state nanopores was inspired by one such work by

Gibrov et al. [81.55] and these are the next most ideal

replacement for biological nanopores owing to several

established and foreseen advantages. First, as for other

chemical sensors, sensitive electronic circuitry and pho-

tonic sensing capabilities can be integrated directly into

a pore–membrane system. Secondly, simultaneous and

automated analysis of hundreds of arrays of different

channels can potentially be achieved with such an inte-

grated system. Next, they are more robust to withstand

wide range of temperature, analyte solution properties,

environments, and chemical treatments that might be

required for target detection and to eliminate interfer-

ence. Finally, these can be customized to ﬁt in practical

biosensors. These properties have heightened the inter-

est in solid-state nanopores, with particular attention as

progenitors of rapid and cheap next-generation DNA

sequencing machines.

In an earlier report on solid-state nanopores, Li

et al. utilized a feedback-controlled ion-beam sculpt-

ing process to make a nanopore in a silicon nitride

membrane [81.56]. A bowl-shaped cavity was made in

a silicon nitride membrane and the material was re-

moved from the other side of this membrane using Ar

ion-beam sputtering. As soon as the ion-sculpted side

reached the bottom of the cavity a hole around 60nm

was opened. Continuous ion-beam exposure reduced

the hole to 1.8nm diameter and ultimately closed it.

Two mechanisms were proposed to account for the pore

size reduction: surface matter moving due to reduced

viscosity to relax the stress caused by implantation, or

the creation of adatoms on the surface by incident ions

that could diffuse to close the pore. A 500 bp dsDNA

translocation experiment was donewith a 5nm diameter

pore. Comparative translocation measurements on 3000

and 10000 bp dsDNA with 3 and 10nm pores were also

reported [81.57]. Longer DNA translocation was noted

to be more complex because of folding.

Dekker’s group reported the fabrication of a nano-

pore with electron-beam lithography EBL and trans-

mission electron microscope TEM techniques [81.3].

Their method realized an in situ observationof pore size

while the size was precisely controlled at the nanome-

ter scale. Chang et al. reported a similar approach,

although developed independently [81.58]. They fab-

ricated 50–60nm long 4–5nm diameter nanopore

channels (NPC), in micromachined Si membranes. The

NPCs were fabricated in a double-polished silicon-

on-insulator (SOI) wafers. They used EBL to initially

deﬁne the pore and fabricated 3–4nm nanopores with

standard solid-state processing. The pore was exam-

ined visually by using TEM while its diameter shrank

to the desired size. The pore shrinkage occurred under

an electron beam of high energy. However, their mecha-

nism was completely different from Li’s process. In this

Part H 81.4

1444 Part H Automation in Medical and Healthcare Systems

a) b) c)

d) e) f)

g) h) i)

nm 20

Fig. 81.8 Pore shrinking temporal proﬁle of a nanopore channel or-

dered alphabetically. All micrographs are taken at 1 000000 ×. The

pore shrinking was stopped at size 16×18nm

. The pore would

shrink further if continuously exposed to the TEM electron beam.

The scale bars are 20nm

process, the electron beam (e-Beam) locally ﬂuidized

the oxide around the pore, and hence oxide ﬂowed to-

wards the pore and then ﬁlled it, as shown in Fig.81.8.

The nanopore die was sandwiched between twosilicone

rings and placed in a ﬁnely milled pocket within Teﬂon

blocks separating the chambers. The Teﬂon blocks

were clamped together and the pore provided the only

path for DNA translocation. A 200bp fragment from

the human CRISP-3 gene was polymerase chain reac-

tion (PCR) ampliﬁed and was used for measurements.

Ag/AgCl electrodes were used to make the ionic cur-

rent measurements. As the dsDNA passed through the

pore, it modiﬁed the bulk and the interface currents,

resulting in typical current pulses, but the pulses were

upwards, unlike in previous studies. The results were

explained, and later conﬁrmed [81.59], by the charge on

the DNA which can be detected in the nanopore channel

due to an inherent charge ampliﬁcation. The condensed

ions on the DNA backbone ampliﬁed the ionic current

in conjunction with the mobile surface charges, similar

to a ﬁeld-effect transistor.

Nanopore technology has attracted more attention

from a number of research groups in recent years. Re-

search has focused in a variety of directions: towards

improving the structures, reducing the time to fabri-

cate, ﬁne-tuning noise parameters, studying the effects

of changing voltages, studying force kinetics, exploring

conformation changes of molecules, and most impor-

tantly the continuous use of nanopores in investigating

various biophysical properties of DNA. Chen et al. em-

ployed atomic-layer deposition (ALD)ofaluminato

controllably shrink the pore size to required nanome-

ter dimensions. ALD was shown to reduce the noise of

the pore and change the surface properties with the pas-

sivation effects of deposited alumina ﬁlm [81.60]. The

same group compared dsDNA translocation through

nanopores of different channel lengths: nanopore in

a thin membrane and nanochannels through a thicker

membrane. They showed that DNA of varying lengths

(3, 10, and 48.5kbp) all traveled at the same veloc-

ity through both types of nanopores. In contrast to the

nonlinearity in mobility versus electric ﬁeld in gel elec-

trophoresis, they showed that the DNA electrophoretic

mobility is independent of the strength of the applied

electric ﬁeld and the length (molecular weight) of the

DNA. It is interesting to note here that size separation

in gel electrophoresis is based on the length-dependent

mobility of the DNA. In another study, the effects

of imaging beam of a TEM through nanopores with

various geometries have also been studied [81.61]. It

was shown that pores smaller than a certain critical

size shrank while larger ones expanded, on the same

wafer, agreeing with the hypothesis that surface tension

effects drove the modiﬁcations. The chemical composi-

tion inthe poreregion was alsodetermined, proving that

contamination growth was not the underlying mech-

anism of pore closure. In another approach to make

nanopores, Ho et al. used tightly focused e-Beam to

make nanopores in 10 nm thick silicon nitride mem-

branes [81.62]. They measured theionic conductance as

a function of various conditions and found it to be much

larger than the bulk conductivity in case of dilute bath

concentrations, whereas it was found to be comparable

with, or less than, the bulk for high bath concentra-

tions. These observations were explained in terms of

the Debye length, which was larger than the pore ra-

dius for the former case. They also reported consistent

multiscale simulations using molecular dynamics of the

ion transport through the pores. They explained the ion

transport by the coupled Poisson–Nernst–Planck and

Stokes equations solved self-consistently for the ion

concentration, velocity, and electrical potential. The re-

sults suggested the presence of ﬁxed negative charges

on the pore walls, thus the ion proximity to the pore

walls reduced the ion mobility.

In most experiments, DNA translocates the nano-

pores at speeds as high as 27–30bases/μs [81.63]. It

was reported that the translocation speed could be re-

Part H 81.4