Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

Automatic Control in Systems Biology 75.4 Dynamical Models 1345

Two broad classes of methods for SNA have been

developed: metabolic pathway analysis (MPA)andﬂux

balance analysis (FBA) [75.70–72]. MPA computes and

uses the set of independent pathways-generating rays in

Fig.75.7 – that uniquely describe the entire ﬂux space;

owing to the algorithmic complexity, it can currently

only handle networks of moderate size. FBA, in con-

trast, determines a single ﬂux solution through linear

optimization [75.73], often assuming that cells try to

achieve optimal growth rates. The computational costs

are modest, even for genome-scale models. The ap-

proach was successful, for instance, in predicting the

effects of gene deletions and the outcomes of conver-

gent evolution in microorganisms [75.72,74,75]. FBA,

however, hasto reverse-engineerand operate with an es-

sentially unknown objective function. While maximal

growth has proven to be a reasonable assumption for

lower organisms [75.76], higher cells may tend to min-

imize overall ﬂuxes in the network [75.77]. In general,

FBA has proven effective for simpler organisms, and

when the steady-state assumption is valid. However,

there are many situations where these conditions do

not apply, many of which are biophysically meaningful,

such as the dynamic diauxic shift in E. coli.

Extensions: Dynamics and Control

Stoichiometric constraints restrict the systems dynam-

ics. Thus, the stoichiometric matrix N is fundamental

not only for SNA but also for dynamic processes in re-

action networks, in which the reaction rates r in (75.2)

are time-dependent. For biological systems, the conser-

vation of total amounts of certain molecular subgroups

(conserved moieties such as ATP, ADP and AMP) is

characteristic and can be exploited for systems analy-

sis. Classical work in chemical engineering addressed

this topic for chemical reaction networks. For instance,

Feinberg derived theorems to determine the possible

dynamic regimes, such as multistability and oscilla-

tions, based on network structure alone [75.78, 79].

Challenges posed by biological systems led to re-

newed interest in these approaches and induced further

theory development [75.80, 81]. Application areas in

biology include stability analysis [75.80] and model

discrimination by safely rejecting hypotheses on re-

action mechanisms, thus identifying crucial reaction

steps [75.82]. Algorithms for the identiﬁcation of de-

pendent species in large biochemical systems – to be

employed, for instance, in model reduction – have re-

cently become available [75.83].

Enabling FBA to deal with dynamics and regulation

proceeded by incorporating additional time-dependent

constraints that reﬂect knowledge of the operation

of cellular control circuits – an approach termed

regulatory FBA [75.84]. For instance, using superim-

posed Boolean logic models to capture transcriptional

regulatory events has extended the validity of the

methodology for a number of complex dynamic sys-

tem responses [75.84] and for data integration [75.85].

Other dynamic extensions of the FBA algorithm have

been proposed in [75.86]. With these more detailed

models, steady-state analysis suggested that the com-

plex transcriptional control networks operate in a few

dominant states, i. e., generate simple behavior [75.87].

Finally, pathway analysis also allows one to approach

features of intrinsically dynamic systems: for instance,

it helps to identify feedback loops in cellular signal

processing [75.88]. Hence, SNA-related approaches are

about to extend to nonclassical domains, in particular,

through theory development induced by new challenges

in systems biology.

Functional Constraints, Optimality, and Design

In analyzing living systems, one possibility is to start

from the assumptions that they have to fulﬁll certain

functions and that cells have been organized over evo-

lutionary time-scales to optimize their operations in

a manner consistent with mathematical principles of

optimality. FBA demonstrates the utility of this assump-

tion; note that its implicit functional constraint, i. e.,

steady-state operation of metabolic networks, is not

self-explanatory. Similarly, other approaches invoking

principles of optimal control theory have opened new

avenues for systems analysis in biology.

The cybernetic approach developed by Kompala

et al. [75.89]andVa rn er and Ramkrishna [75.90]is

based on a simple principle: evolution has programmed

or conditioned biological systems to optimally achieve

physiological objectives. This straightforward concept

can be translated into a set of optimal resource allo-

cation problems that are solved at every time-step in

parallel with the model mass balances (basic metabolic

network model). Thus, at every instant in time, gene ex-

pression and enzyme activity are rationalized as choice

between sets of competing alternatives, each with a rel-

ative cost and beneﬁt for the organism. Mathematically,

this can be translated into an instantaneous objective

function. The researchers in this area have deﬁned sev-

eral postulates for speciﬁc pathway architectures, and

the result is a computationally tractable(i.e., analytical)

model structure. The potential shortcoming is a limited

handling of more ﬂexible objective functions that are

commonly observed in biological systems [75.91–95].

Part H 75.4

1346 Part H Automation in Medical and Healthcare Systems

Instead of focusing on a single objective func-

tion, mathematical models and experimental data can

be used to test hypotheses on optimality principles,

given a speciﬁc cellular function to be fulﬁlled. For

instance, extensions of FBA suggested that E. coli opti-

mizes the tradeoff between achieving high growth rates

and maintaining wild-type metabolic ﬂuxes after gene

deletions [75.96]. MPA showed that the interplay be-

tween the metabolic network (the controlled plant) and

gene regulation (the controller) in E. coli might be de-

signed to achieve optimal tradeoffs between long-term

objectives, such as metabolic ﬂexibility, and short-term

adjustment for metabolic efﬁciency [75.97]. Optimal

production pipelines for biomass components, with fast

responses to environmental changes and minimal addi-

tional efforts for enzyme synthesis, were predicted in

detail to employ wave-like gene expression programs,

which was later conﬁrmed experimentally [75.77, 98].

Hence, at least certain cellular design principles can be

revealed by evaluating assumptions on cellular optimal-

ity principles.

Finally, without assuming optimality, we can ask

how functions in biological systems could be es-

tablished in principle. Among others, drawing from

analogies with engineered systems helps to understand

more general design principles in biology. From non-

linear dynamics, for instance, it is well-known that

functions such as oscillators and switches require some

source of nonlinearity. Establishing sucha functionwith

biological building blocks, thus, allows only for cer-

tain circuit designs [75.99,100]. Similar ideas can prove

powerful at different levels of abstraction. For instance,

highly structured bow-ties with multiple inputs, chan-

neled through a core with standardized components and

protocols to multiple outputs, could be the common

organizational principles to establish complex produc-

tion systems in engineering and biology [75.53]. On

the other hand, El-Samad and colleagues studied the

bacterial heat-shock response, pointing out that the in-

tertwined feedback and feedforward loops present can

be assigned individual functions parallel to those loops

in designed control circuits that have to yield fast re-

sponses in highly ﬂuctuating environments [75.101].

Notably, most of the examples discussed here involved

newdevelopmentsin theory toaddress challenges posed

by biology.

75.5 Network Identiﬁcation

Model development involves the translation of identi-

ﬁed biological processes to coupled dynamical equa-

tions, which are amenable to numerical simulation

and analysis. These equations describe the interac-

tions between various constituentsand the environment,

and involve multiple feedback loops responsible for

system regulation and noise attenuation and ampliﬁca-

tion. Currently, however, our knowledge of essentially

all biological systems is incomplete. Despite genome

projects that allow enumeration and, to a certain ex-

tent, characterization of all genes in a system, this

does not imply knowledge about all network compo-

nents (for instance, all protein variants that can be

derived from a single gene), interactions, and properties

thereof [75.22]. An important task in systems biology

consists of specifying network interactions, which can

concern qualitative or quantitative properties (existence

and strength of couplings), or detailed reaction mecha-

nisms, for genome-based inventories of components.

Essentially, this is a systems identiﬁcation prob-

lem. Given a set of experimental data and prior

knowledge, the network generating the data is to be

determined [75.102]. Alternatively termed reverse en-

gineering [75.103], network reconstruction [75.104]or

network inference [75.105], the general network iden-

tiﬁcation problem provides a key interface between

science and engineering. Several qualitatively different

approaches for biological systems have been proposed,

which can be roughly classiﬁed into three categories:

data-driven, approximative and mechanistic.

75.5.1 Data-Driven Methods

Empirical or data-driven methods rely on large-scale

datasets that can be generated, for instance, through

microarray analysis for gene regulatory networks.

The relevant methods include singular value decom-

position analysis of microarray data [75.106, 107],

self-organizing maps [75.108], k-means clustering or

hierarchical clustering [75.109], protein correlation and

dynamic deviation factors [75.110], and robust statis-

tics approaches [75.111, 112]. For instance, clustering

methods are routinely applied for identifying groups of

coregulated genes from microarray data. The interpre-

tation of clustering results employs (implicit) models

such as coexpressed genes that are likely to have a com-

Part H 75.5

Automatic Control in Systems Biology 75.5 Network Identiﬁcation 1347

mon regulator. Data quality andalgorithmic choices (for

instance, of distance measures) critically inﬂuence the

clustering results; in addition, validation of clustering

results and techniques is an open issue [75.113–115].

In contrast to the mechanistic approaches discussed

later, most empirical approaches employ discrete-time

gray box models [75.116–119]. For instance, infer-

ence methods based on probabilistic graphical (e.g.

Bayesian) models help to elucidate causal couplings

between the network components [75.120]. Their scal-

ability for large systems and the ability to integrate

heterogeneous datasets make them attractive [75.5,

121]. Yet, these approaches deliver only qualitative

descriptions of network function, and have inherent lim-

itations. For instance, Bayesian models cannot cope

with the ubiquitous feedback in cellular networks, since

causal relationships have to be represented by directed

acyclic graphs [75.120].

A number of challenges are present in treating ex-

perimental data for such problems: (1) the sampling rate

is rarely uniform and may be exponentially spaced by

design, and (2) data from multiple research groups are

often combined (e.g. from WWW-posted data) to yield

data records with inconsistent sampling, experimen-

tal bias, etc. From a systems engineering perspective,

another critical point is the potentially divergent qual-

itative behavior between continuous-time and discrete-

time models of corresponding order [75.122]. Recent

work has shown the promise of continuous-time formu-

lations of empirical models using modulating function

approaches [75.40].

More generally, correctly identifying network

topologies (corresponding to the model structure)

clearly does not sufﬁce for establishing predictive

mathematical models. Experiences with engineered

genetic circuits illustrate this point: with identical topol-

ogy, qualitatively different behavior can result and

vice versa [75.123]. Hence, quantitative characteris-

tics, which are usually incorporated through parameters

in deterministic models, are also required. Corre-

sponding identiﬁcation methods are rooted in systems

and information theory and, thereby, also provide the

largest intersection among biology, other sciences, and

engineering.

75.5.2 Linear Approximations

The identiﬁcation of dynamically changing interac-

tions requires corresponding dynamic models. In a ﬁrst

approximation, we can consider linear systems, i.e.,

systems with additive responses to perturbations. In

systems engineering, a standard form for linear time-

invariant (where the shapeof the output does not change

with a delay in the input) systemswith n states andm in-

puts is given by (75.3) with n ×1 state vector x(t), n ×n

system matrix A, n ×m input matrix B,andm ×1 in-

put vector u(t). Linearization of the general dynamic

system dx(t)/dt = f (x, p, t) with parameter vector p

provides ﬁrst approximations to the network dynam-

ics, even for highly nonlinear systems such as those

encountered in biological networks. Linear models cap-

ture the local dynamics, for instance, in the vicinity of

a steady state, instead of aiming at more complicated

global behaviors.

dx(t)

= f(x, p, t) ≈Ax(t)+Bu(t)

(75.3)

Mathematically, most methods reconstruct the system

matrix A, which corresponds to the Jacobian matrix

J =∂ f(x, p)/∂x, from the measured effects of (sufﬁ-

ciently small) perturbations. However, direct recovery

of the system matrix A will be unreliable with noisy

data and inputs. In a study using linear models and

perturbation experiments to identify the structure of

genetic networks, Tegner et al. [75.103] therefore pro-

posed an iterative algorithm that uses rational choices

of perturbations to improve the identiﬁcation quality.

For a developmental circuit, despite high nonlinearities

in the system, the reverse engineering algorithm, which

involves building and reﬁning an average connectivity

matrix in successive steps, recovered all genetic inter-

actions [75.103]. A related approach that uses linear

models and multiple linear regressions showed simi-

lar performance. The algorithm attempts to exploit the

sparsity of systems matrices for biological networks

owing to, for example, (estimated) upper bounds on the

number of connections per node [75.105, 124]. Both

algorithms are scalable – a central concept in engineer-

ing, but until recently considered of less importance in

biology.

Newer approaches to systems identiﬁcation aim

at exploiting modularity in biological networks. For

a modular system with one output per module, the

method employsinversion of the global response matrix

for identiﬁcation of network connectivities and of lo-

cal responses from perturbation experiments [75.125].

It requires a reduced number of measurements com-

pared with other methods because only changes in

so-called communicating intermediates have to be

recorded. Apparently, some simplifying assumptions

have to be made; for example, modules are coupled

by information ﬂow only, and mass ﬂow is negligi-

Part H 75.5

1348 Part H Automation in Medical and Healthcare Systems

ble [75.125]. An important result of extending the

modular identiﬁcation to time-series data is that, for

identifying all connections of a node, it is not nec-

essary to perturb this node directly – inference can

rely on detecting the network responses to remote

perturbations [75.126]. Extensions to include the ef-

fects of uncertainties in experimental data and prior

knowledge [75.127], and the possibility of a uniﬁed

mathematical framework [75.128] make modular iden-

tiﬁcation methods particularly promising.

75.5.3 Mechanistic Models, Identiﬁability

and Experimental Design

Mechanistic models, owing to effects such as saturation

in enzymatic reactions, pose particular challenges be-

cause they involve identiﬁcation of nonlinear systems.

Depending on whether model structure and parame-

ters, or only the parameters have to be identiﬁed, the

problems fall into the classes of mixed-integer nonlin-

ear programs or nonlinear programs, respectively. As

a clear limitation, ﬁnding a unique global optimum in

the estimation, or convergence of the algorithms cannot

be guaranteed. In addition, model identiﬁcation comes

at high computational costs owing to numerous model

simulations [75.129].

In terms of parameter estimation, which is a com-

mon problem in different scientiﬁc domains [75.102],

realistic modeling of complex, nonlinear dynamics of

biological networks has given new impulses for the

evaluation of existing methods and development of new

methods. For instance, though stochastic algorithms

show superior performance over deterministic meth-

ods for parameter optimization in these systems, they

are computationally expensive [75.130]. Novel hybrid

methods try to exploit synergies between both ap-

proaches in order to increase robustness and efﬁciency

(e.g. [75.131, and references therein]).

More fundamentally, identiﬁability and design of

informative experiments need to be addressed. Unstruc-

tured approaches to model identiﬁcation are completely

ill-posed when faced with, for instance, modeling

a yeast cell with 6200 genes and four possible states

per gene; we obtain an overall expression state dimen-

sioninexcessof10

[75.132]. Clearly a number of

a priori constraints and correlations must be exploited.

For discrete models, usage of the experimentally ob-

served upper bound on the number of interactions per

species brings the amount of data needed for identi-

ﬁcation into realistic dimensions [75.133]. However,

mere extrapolation of current high-throughput technol-

ogy will not solve these high dimensional data issues.

Several recent studies have highlighted the importance

of proper design of perturbations to reveal the logical

connectivity of gene networks [75.104, 134]. Systems

engineering concepts of experimental design to pro-

vide rich datasets can be exploited to develop predictive

mechanistic models.

Parameter estimation accuracies are central to mea-

suring identiﬁability of mechanistic models. Low accu-

racies mean that the corresponding parameters may be

varied to a greater extent – and still describe the data –

than it is possible for parameters with high estimation

accuracy (low associated error). They combine infor-

mation on model sensitivities with experimental data

(Fig.75.8). More speciﬁcally, the Fisher information

matrix (FIM) F(p) [75.135], for a point in parameter

space p, links model and experiment via state sensitiv-

ities S(t) =∂x/∂ p and measurement covariance matrix

for a discrete sampling time t

, C(t

). For an unbiased

estimator, the Cramér–Rao theorem then gives a lower

bound for the estimation error (minimum variance).

FIM-based approaches, for instance, yielded insight

into the importance of suitable design of input per-

turbations for signaling networks [75.40], optimality

criteria for the design of such inputs [75.136], and al-

gorithms for the optimization of sampling times for

dynamic experiments [75.137]. New hybrid parameter

estimation methods [75.131] and closed-loop (i.e., inte-

grating iterations between estimation, evaluation of the

identiﬁability, and experimental design) optimal identi-

ﬁcation procedures [75.138] rely on the FIM formalism.

Note, however, that while these proof-of-concept stud-

ies with small models and synthetic data are valuable,

the performance for real biological problems awaits

assessment.

Mathematical model

Parameter sensitivities

Fisher information matrix: F(p) =

Quality of identification: σ

≥

S(t

)

–1

) S(t

)

Experimental data

Measurement

covariance matrix C

S(t) =

∂x(t)

∂p

x = x(t,p), p = p

[

F(p)

–1

[

i=1

Fig. 75.8 FIM and identiﬁcation quality. The lower bound

for the estimation error of parameter j, σ

, is derived from

the inverse of the main diagonal of the FIM (after [75.4])

Part H 75.5

Automatic Control in Systems Biology 75.6 Quantitative Performance Metrics 1349

Information-rich datasetsfor integrative models will

have to be derived from sources across all levels

of biological regulation, such as the transcriptome,

proteome, and metabolic ﬂuxes. Concomitantly, we

need novel statistical frameworks for data integra-

tion [75.139]. Systems identiﬁcation would greatly

beneﬁt from the direct in vivo determination of ki-

netic parameters; the work by Ronen et al. [75.140]

for transcriptional control is a ﬁrst step in this direc-

tion. As a complement, synthetic genetic circuits could

provide means for controlled excitation of the system,

for instance, by inducible genetic switches [75.103],

or through genetic oscillators to incorporate analysis

methods inthe frequencydomain [75.102].Novel meth-

ods could also take known uncertainties associated with

measurements, suchas experimentally determined char-

acteristics of stochastic noise, explicitly into account.

Finally, identiﬁcation depends on adequate speciﬁca-

tion of the system and model (e.g., [75.141]). While

models are currently either set up ad hoc, or through

manual comparison of few alternative structures (in-

cluding kinetic terms in the equations), uncertainties in

biology pose a major challenge for systems sciences:

deriving advanced approaches to model discrimination

for the simultaneous identiﬁcation of model structures

and parameters.

75.6 Quantitative Performance Metrics

In biology, as in engineering, robust performance refers

to the attainment of a particular behavior or response by

a system in the presence of uncertainty. This appears to

be a ubiquitous property of biological processes that are

subject to constant uncertainty in the form of stochas-

tic phenomena [75.142], ﬂuctuating environment, and

genetic variation (reviewed in [75.15]). Biology has

adapted a number of approaches for coping with these

sources of uncertainty, which include:

1. Back-up systems (redundancy)

2. Disturbance attenuation through feedback and feed

forward control

3. Structuring of networked systems into semi-

autonomous functional units (modularity)

4. Reliable coordination of network elements through

hierarchies and protocols.

The robustness problems in systems biology have

only begun to yield, in recent years, formal quanti-

tative analyses, owing largely to their nonlinear (and

nonstationary) nature. As with engineering systems, ro-

bust performance requires the precise speciﬁcation of

both a performance metric and the type/size of uncer-

tainty. When both these elements are speciﬁed, it may

be possible to analyze biological systems with estab-

lished engineering tools. It is important to note that

the performance metric is often difﬁcult to be deﬁned

precisely in biology, as it is an implicit element of an

evolved entity.

The last 10 years have demonstrated that sensi-

tivity analysis can provide unique insights into the

functioning of complex biophysical networks [75.4,

143–145]. Of particular interest is the behaviour of

biological circuits that exhibit oscillations (e.g., circa-

dian rhythm, cell cycle, neuron ﬁring, cardiac cycles,

etc.). In [75.146], a novel set of sensitivity metrics

was introduced for performance that were based on

a number of different phase-measures: period, phase,

corrected phase, and relative phase. The motivation

was that phase appears to be the biological imperative,

rather than period, for optimal regulation of circadian

rhythms. Both state-based and phase-based tools were

applied to free-running (absence of light/dark cycles)

Drosophila melanogaster and Mus musculus circadian

models. Each metric produced unique relative sensitiv-

ity measures used to rank parameters from least to most

sensitive. Similarities among the resulting rank distri-

butions strongly suggested a conservation of sensitivity

with respect to parameter function and type. A con-

sistent result, for instance, is that model performance

of biological oscillators is more sensitive to global pa-

rameters than local (i.e., circadian speciﬁc) parameters.

Differences across the metrics revealed that the conclu-

sions about robustness were dependent on the metric

employed for performance.

In [75.147], a novel sensitivity measure, the para-

metric impulse phase response curve (pIPRC), was

derived to both characterize the phase behavior of an

oscillator and provide the means for computing the

response to an arbitrary signal (in the form of paramet-

ric perturbation). The pIPRC builds on the knowledge

that biologists have collected for decades in the form

of phase response curves (PRCs), to more general

classes of input perturbations. The PRCs and inﬁnitesi-

mal PRCs presented in that study provided quantiﬁable

measures of robustness for oscillators acting as pace-

Part H 75.6

1350 Part H Automation in Medical and Healthcare Systems

makers. In these systems, robust performance involves

proper maintenance of phasebehavior. In the case ofthe

circadian clock, this means that the PRC to light must

have notonly theproper shape, but alsothe correct mag-

nitude. Zeilinger et al. [75.148] were able to invalidate

a model of the circadian clock in the plant Arabidop-

sis thaliana, because the pIPRC had neither the proper

shape nor the proper magnitude.

In [75.149], sensitivity methods were employed to

predict the likelihood that noise propagates in stochas-

tic models of the circadian network. The results showed

that noise introduced into a sensitive point in the clock

propagates very well, while noise introduced into an

insensitive (or robust) point is undetectable elsewhere.

The noise propagates without regard to distance from

point of introduction to point of measurement. It was

concluded that the sensitive global parameters are the

sites of effective noise propagation in the clock. The hy-

pothesis was that global parameters govern reactions at

critical points in the network and therefore may suggest

those parts of other systems most worthy of investiga-

tion.

The previous studies focused on single cell models,

but network properties must also be analyzed at higher

levels in the system. Bagheri et al. [75.150] demon-

strated that computational techniques applied to single

cell data are fundamental for tuning and predicting the

behavior of oscillatory phenomena at the population

level [75.151], since the results of such investigations

point to the coupling mechanisms that give rise to

spontaneously synchronized networks of stochastic bio-

physical nodes. Without such insight, it would not have

been possible to reproduce the synchrony observed in

the SCN. As a result, it is important for experimental

biologists to adopt the tools necessary to analyze the

structure of both in vitro and in vivo systems.

75.6.1 State-Based Sensitivity Metrics

Parametric state sensitivity is captured in an m by

n matrix consisting of individual state performance

values with respect to isolated parametric perturba-

tions. The direct method [75.152, 153] is a means

to determine exact parametric state sensitivity mea-

sures, S

(t) = dx

(t)/dρ

. This approach relies on the

continuity of f[x(t), ρ] with respect to the parameter

vector ρ. Applying the chain rule results in partial

derivatives of the function with respect to states and pa-

rameters produces an ordinary differential equation of

sensitivity dynamics (75.4). The initial conditions for

the sensitivities are zero unless the system initial condi-

tions x

depend on the parameters.

S(t) =

∂ f[x(t), ρ]

∂x

•S(t)+

∂ f[x(t), ρ]

∂ρ

(75.4)

In oscillatory systems, coefﬁcients of raw state sensitiv-

ity, S(t) = dx(t)/ dρ, rely on multiple coupled outputs

(such as period and phase) and grow unbounded in

time for parameters whose period sensitivities are

nonzero [75.154–156]. The secular term is due to com-

putation of sensitivities involving a nonuniformly valid

expansion of a periodic system [75.154]. Tomovic and

Vukobratovic [75.155] demonstrate that state sensitiv-

ity, evaluated at the constant nominal period τ, provides

a speciﬁc measure corresponding to limit cycle be-

havior. This measure is unbiased to changes in the

period/frequency of oscillation. The resulting m by n

matrix is referred to as the cleaned-out or shape sensi-

tivity measure S

(t) =(∂x(t)/∂ρ)

; S

(t) is periodic in

time and describes how parametric perturbations affect

the shape of state trajectories [75.154]. In its raw form,

state sensitivity for oscillatory systems may be decom-

posed intoa combination of shape andperiod sensitivity

measures (75.5) [75.155]. This decomposition of raw

state sensitivity highlights its linear time growth t/τ

while isolating period sensitivity, S

= dτ/dρ. The de-

composition is generally accomplished by calculating

state and period sensitivities, and then solving for the

cleaned-out shape sensitivity matrix.

S(t) = S

(t)−

f[x(t),ρ]

dτ

dρ

(75.5)

Zak et al. [75.156] proposed a method to determine pe-

riod sensitivity S

by making use of the decomposition

(75.5) and evaluating state sensitivities at a large time

*τ. At this time, the second term on the right-hand

side of (75.5) dominates the cleaned-out sensitivity ma-

trix. Singular value decomposition of state sensitivity

produces S(t

) =UV



, where  is an m by n di-

agonal matrix of nonnegative singular values σ and

matrices U and V contain the eigenvectors of SS



and S



S, respectively. Hence, period sensitivity of any

given state may be approximated by (75.6) where σ

the largest singular value in , f[x(t

)], ρ is the vec-

tor norm of the state matrix evaluated at time t

,and

is the ﬁrst column vector of V. This approximation

holds true at any large times t *τ, when the system is

nonzero, and when the period of oscillation is sensitive

to at least one parameter [75.156].

≈±

f[x(t

)], ρt

(75.6)

Part H 75.6

Automatic Control in Systems Biology 75.6 Quantitative Performance Metrics 1351

Amplitude sensitivity S

∧

describes how maximum state

values vary due to independent parametric perturba-

tions. As discussed, cleaned-out sensitivity deﬁnes how

parametric perturbations affect the shape of state trajec-

tories at every time in the cycle; at peak concentration

times this measure relates directly to the state’s maxi-

mum concentrations. Thus, amplitude sensitivity values

are calculated from shape sensitivity by evaluating the

time-dependent measure (75.7) at peak concentrations

times t

peak

∧

peak

) . (75.7)

75.6.2 Phase-Based Sensitivity Metrics

In cases involving oscillatory networks and often noisy

state amplitude data, phase may be employed as a met-

ric for model development and analysis. Standard (raw)

phase and decoupled (corrected) phase are among

the set of numerical performance measures introduced

in [75.146]. Radian-based phase angles θ(t,ρ) are ex-

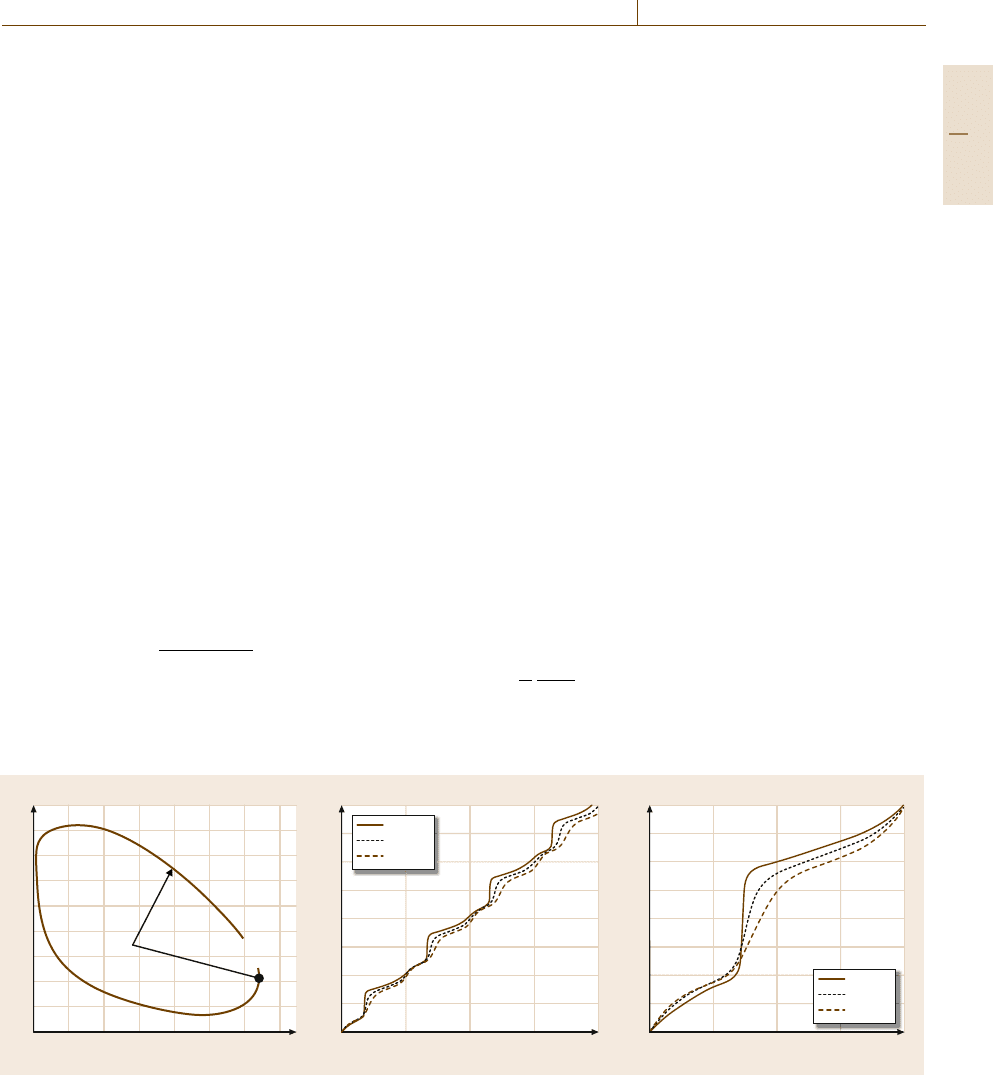
tracted from the system’s limit cycle (Fig.75.9a) using

the cosine rule [75.158]. Resulting phase dynamics re-

ﬂect the oscillator’s real-time position, or concentration

(75.8), with respect to a static reference r

cos[θ(t, ρ)]≈±

x(t,ρ)



x(t, ρ)r

(75.8)

Phase measures are recorded under varying parameter

sets, θ(t,

ρ), where

ρ indicates measurements with re-

spect to a perturbation of magnitude δ affecting a single

a) Protein concentration (nM)

mRNA concentration (nM)

0.4 0.8 1.2 1.6 2

θ (t)

2.4 2.8

1.6

1.2

0.8

0.4

b) Phase (rad/π)

Time (h)

96724824

c) Phase (rad/π)

Percent of a single cycle

100755025

7/4

3/2

5/4

3/4

1/2

1/4

1.15 v

1 v

0.85 v

1.15 v

1 v

0.85 v

Reference

vector

Real-time

state vector

Fig. 75.9a–c Time-dependent phase dynamics. (a) Real-time phase dynamics captured in a 2-D limit cycle. Phase is the radian-

based measure θ(t, ρ) that describes the angular relationship between the state vector x(t, ρ) and some predetermined reference r.

Phase measures are recorded as a function of time under various parameter sets.

(b) Coupling of period and phase as trajectories

diverge in time.

perturbation-induced periods (after [75.146,157] by permission of Oxford University Press)

parameter ρ

. This perturbation changes the nominal

parameter vector from ρ to a perturbed parameter vec-

tor ρ

ρ =ρ +δe

, ∀j ∈[1, n]. (75.9)

The collected phase trajectories capture the oscillator’s

position and map them onto nominal time (Fig. 75.9b).

If the perturbation strength and length are the same, the

information contained in these trajectories is analogous

to thatcontained in phase transitioncurves [75.159]. Di-

rect evaluation of phase trajectories (Fig.75.9b) yields

two types of sensitivity measures: period and phase,

because the change in period (or period sensitivity)

is merely an accumulation in the change in phase (or

phase sensitivity) evaluated over an entire cycle. In

the case of period sensitivity, phase trajectories are

evaluated at a 2π L-radian interval, where the integer

interval L is chosen to balance the numerical error

with computational expense. The difference between

the perturbed 2π L-radian crossing time

k and the nom-

inal 2π L-radian crossing time k yields the system’s

periodic performance. A normalized time difference be-

tween perturbed and nominal phase trajectories deﬁnes

the system’s period sensitivity, S

(75.10): a series of

measurements denoting the quantitative change in pe-

riod with respect to a change in the j-th parameter

k−k

δρ



θ(k,ρ)=θ(

ρ)=2π L

∀j ∈[1, n], L ∈[1, ∞) .

(75.10)

Part H 75.6

1352 Part H Automation in Medical and Healthcare Systems

In the case of strict phase sensitivity, one can evalu-

ate phase trajectories at speciﬁc times t =t

. The radian

phase difference between perturbed and nominal trajec-

tories describes the raw phase sensitivity, S

(75.11):

a series of measures reﬂecting the induced change in

phase with respect to a change in the j-th parameter

-hours after the perturbation

θ(t,

ρ)−θ(t, ρ)

δρ



t=t

, ∀j∈[1, n]. (75.11)

–2

d) e)

(Phase) Period sensitivity (h/nM)

(State) Period sensitivity (h/nM)

–1

–2

Autoinhibition

Transcription

Translation

mRNA degradation

Protein degradation

Complex degradation

Unspecified degradation

(De)phosphorylation

(Dis)association

Transport

0 10 20 30

b) Relative phase ranking

Corrected phase ranking

Autoinhibition

Transcription

Translation

mRNA degradation

Protein degradation

Complex degradation

Unspecified degradation

(De)phosphorylation

(Dis)association

Transport

Most

sensitive

Degradation

Degradation, complex

Degradation, mRNA

Degradation, protein

Transport

Translation

Transcription

Expression

(Dis)association

Phosphorylation

Dephosphorylation

Global

State

Amplitude

Shape sensitivity

Period (state)

Period (phase)

Corrected phase

Phase

Relative phase

Mixed

Local

Least

sensitive

Most

sensitive

Least

sensitive

c) State ranking

Amplitude ranking

Autoinhibition

Transcription

Translation

mRNA degradation

Protein degradation

Complex degradation

Unspecified degradation

(De)phosphorylation

(Dis)association

Transport

Most

sensitive

Degradation

Degradation, complex

Degradation, mRNA

Degradation, protein

Transport

Translation

Transcription

Expression

(Dis)association

Phosphorylation

Dephosphorylation

Global

State

Amplitude

Shape sensitivity

Period (state)

Period (phase)

Corrected phase

Phase

Relative phase

Mixed

Local

Least

sensitive

Most

sensitive

Least

sensitive

0102030

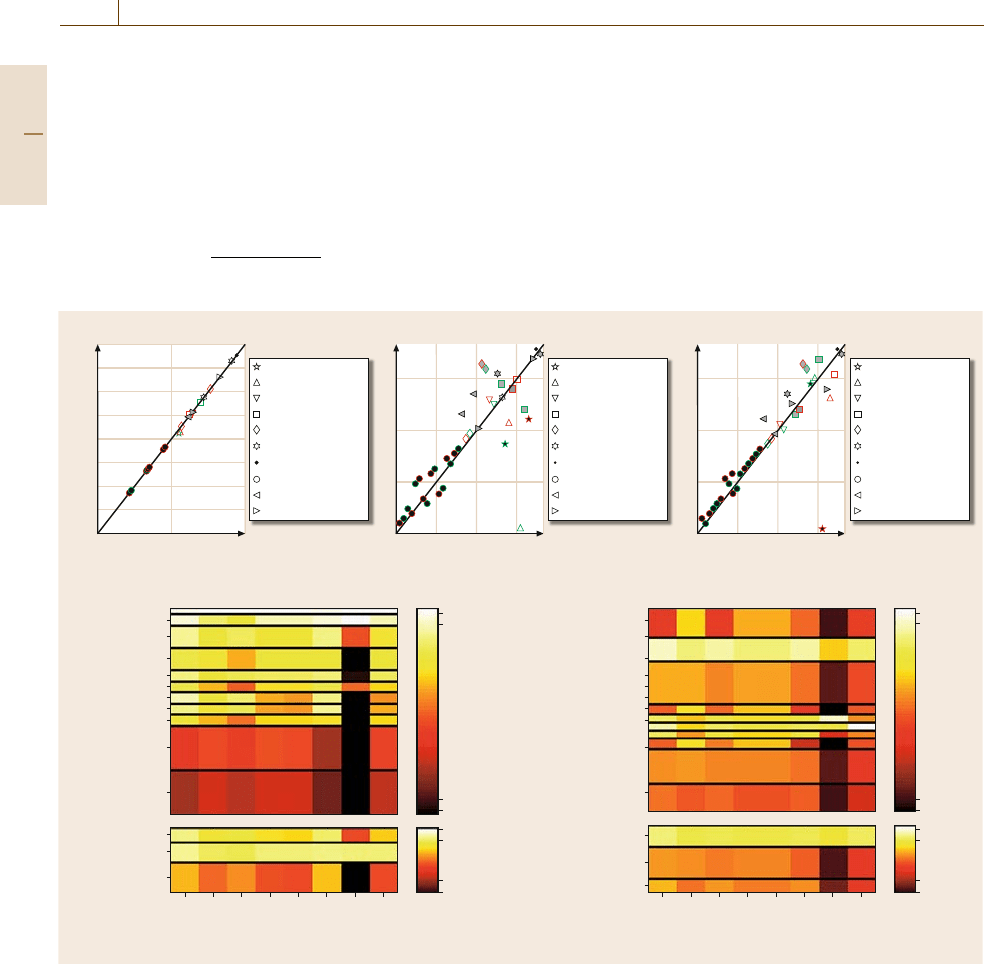
Fig. 75.10a–e Metric evaluation. (a–c) Parametric sensitivity metrics ordered from least to greatest absolute value for the

Drosophila model:

(a) state-based and phase-based period sensitivity, (b) corrected phase (decoupled angular phase trajecto-

ries) and relative phase (time interval between peak per mRNA and nuclear PER/TIM protein concentrations) sensitivity ranks

and

(c) amplitude-based and state-based metrics. Spearman rank correlation coefﬁcients for these pairs of metrics are 1.00, 0.64

and 0.85, respectively. Legends describe the parameters’particular biological processes as the shading of each data point describes

their type: global (open), mixed (gray) and local (black) parameters. Data points outlined in red reﬂect per gene dynamics, and

those in green reﬂect tim gene dynamics.

(d,e), Color-coded average sensitivities (values are scaled between 10

−4

and 1) among

parameter function (upper subplots) and parameter type (lower subplots) for each metric in the ﬂy

(d) and the mammalian (e)

model. See the supplementary material for alternate correlation diagrams and ranking plots (after [75.146,157] by permission of

Oxford Univ. Press)

Just as state sensitivity diverges over time, phase

sensitivity grows unbounded due to the nonuniform

expansion of a periodic system. To correct for the inte-

grated response of perturbation effects (in this case, the

coupling of period and phase), each phase trajectory is

normalized with respect to the period of the system af-

ter parametric perturbation

τ: dividing each time series

τ decouples the system’s phase from its period. As

a result, normalized datasets begin and end at the same

relative time points (0 and 100% of their respective cy-

Part H 75.6

Automatic Control in Systems Biology 75.7 Bio-inspired Control and Design 1353

cles). These modiﬁed datasets allow for a comparison

between nominal and perturbed phase at every point

in the cycle (Fig.75.9c). This corrected phase sensi-

tivity assumes a linear scaling of raw phase measures

resulting in a time-dependent performance quantity that

identiﬁes speciﬁc points of the cycle most susceptibleto

uncertainty (75.12)

θ(t/

τ,

ρ)−θ(t/τ, ρ)

δρ

, ∀j∈[1, n]. (75.12)

Phase-based period, phase, and corrected phase sensi-

tivity analysis examine the biological network relative

to a static reference. In some cases, a relative analysis

that studies relationships within the perturbed network

may be more useful. The timing effects relating tran-

scription, translation, phosphorylation,and transport are

governed byglobal cellularprocesses. Variationof these

speciﬁc time intervals as a result of parameter ma-

nipulation indicates a degree of sensitivity. Relative

sensitivity S

investigates the time interval relating the

hour-difference between the occurrence of particular

events; for instance, the time interval between peak

mRNA concentrations and their corresponding protein

concentrations. This time interval φ[x(t), ρ], is a func-

tion of the system’s state and parameter vectors. It

explores how a system’s individual components change

relative to one another due to parametric perturba-

tion (75.13)

φ[x(t),

ρ]−φ[x(t), ρ]

δρ

, ∀j∈[1, n]. (75.13)

75.6.3 Global Versus Local Parameters

The investigated performance metrics depict classes of

sensitivity that associate with parameter function, prov-

ing a certain conservation of robustness for speciﬁc

biochemical processes.A similar sensitivity distribution

was found when parameters were separated into three

types: global, mixed, and local [75.15]. Global param-

eters are involved in core cellular reactions nonspeciﬁc

to the circadian rhythm;they encompass properties con-

sistent with the entirety of the cellular network. Local

parameters are primarily attributed to the circadian sys-

tem; their processes and/or elements are not shared with

many other cellular circuits. Global parameters include

transcription rates, various mRNA and protein degrada-

tion rates, and translation rates.

Figure 75.10a–c depict phase-based and state-based

period sensitivities, relative and corrected phase sen-

sitivities, and amplitude and state sensitivities. Global

parameters were consistently found in the ﬁrst (up-

per right) quadrants of these plots. Local parameters,

including protein phosphorylation and dephosphoryla-

tion, were consistently in the lower left (less sensitive)

corners. Figure 75.10d and e (lower subplots) empha-

size this conservation of sensitivity apparent in both

models by assigning a color reﬂective of the average

sensitivity ranking within each parameter type.

The results demonstrated that every deﬁned per-

formance metric was more sensitive to perturbations

involving global and mixed parameters than it was

to perturbations involving local parameters. Grouping

parametric sensitivity based on parameter type provided

a more consistent and distinct distribution of sensitiv-

ity measures among various metrics than the grouping

of sensitivity by function. This outcome agreed with

a previous study suggesting that circadian performance

is greatly affected by changes in global parameters and

less susceptible to changes in local parameters [75.13,

15].

75.7 Bio-inspired Control and Design

Biological networks offer a number of opportunities

for inspired design of engineering networks. Aside

from the overlapping computational toolkit (e.g., sim-

ulation methods for high dimensional, stochastic, stiff,

multiscale systems), there are numerous behaviors in

biological networks that offer promise for improved

communications and sensors networks. Given the space

constraints, we highlight only two of them here, but re-

fer the reader to the thorough NRC report on network

science for additional details [75.160].

Using control engineering parlance, one may refer

to the elements that inﬂuence or entrain the circadian

oscillator (zeitgeber: time giver) as manipulations, and

the elements that exhibit quantiﬁable circadian rhythms

as measurements. The use of this terminology is re-

ﬂective of the spirit in looking for ways to inﬂuence

rhythms to ﬁnetune physiological performance.Contin-

uing the control analogy, the open-loop characteristics

(i.e., with no intervention) of the typical human are to

adjust at arate ofapproximately 60–90min ofphase per

day [75.161].In otherwords, jet lag accommodation oc-

curs at a rate of approximately 2–3days for a 3 h time

zone change. Westward travel is slightly easier, as the

natural free-running human circadian clock (i. e., in ab-

Part H 75.7

1354 Part H Automation in Medical and Healthcare Systems

sence of light) has a period of approximately 25h. From

a control perspective, the two important attributes of the

resetting response characteristics are phase shift (cap-

tured by the phase response curve), and the associated

transient, which we deﬁne via the transient response

curve.

Sensitivity analysis can be used to develop insight

on the parts of a network that are most sensitive and,

consequently, the most susceptible to intervention such

as the targeting of a drug. However, a typical applica-

tion will require a temporal forcing of a node (or nodes)

in a network to elicit an optimal response. In recent

work, model predictive control (MPC) algorithms have

been employed to generate the optimal forcing proto-

col that will reset the circadian clock from a condition

of phase offset (i.e., jet lag) [75.157, 162]. Through

parametric state sensitivity analysis, key driving mech-

anisms for optimal manipulation of the large complex

circadian network were identiﬁed. Importantly, the use

of nonphotic control inputs outperforms light-based

phase resetting dynamics. Aside from targeting indi-

vidual parameters as control inputs, Fisher information

matrix based parametric sensitivity analyses identiﬁed

combinations of parameters for control (i. e., vector

strategies). The derived MPC algorithm is found to be

robust to model mismatch and outperforms the open-

loop 24h sun cycle based phase recovery strategy by

nearly threefold.

75.8 Emerging Trends

Systems biology has an exciting future. Opportunities

for research exist in the areas of network identiﬁca-

tion, constraints and optimality, stochastic systems, and

robustness [75.4], as well as synthetic approaches to

network reconstruction:

1. Knowledge of biological systems is incomplete,

and codiﬁcation of the interactions among network

components, interactions, and properties requires

continued elaboration. This systems identiﬁcation

problem can be approached via empirical, approx-

imative, and mechanistic methods.

2. An understanding of biological systems may pro-

ceed from an appreciation of constraints, which

can be divided into three classes: (1) Functional

constraints exist because biological systems per-

form speciﬁed functions arising from a ﬁnite set

of components. Since biological systems evolve to

a performance metric, it is sensible to presume op-

timality. This leads to a smaller design space with

highly structured, but rarely composed, reliably

networks.(2) Analysis ofexperimentaldata can pro-

vide data on the possible arrangements for network

structure. (3) The laws of physics and chemistry,

must, of course, be observed.

3. Developments in systems biology will continue

to depend upon algorithmic innovations to ap-

proach stochasticity, particularly for distributed

models.

4. There exist intrinsic scaling problems with those

engineering methods that provide a formal frame-

work for robustness analysis. For large, complex,

nonlinear systems, the methods are conservative

and computational tractability is questionable. Con-

sequently, the scalability of robustness analysis

methodologies provides interesting future chal-

lenges.

One promising application of a systems approach

to biology lies in healthcare [75.163]. Unlike today’s

medicine, with its emphasis on therapies for existing

disease, tomorrow’s medicine will predict and prevent

illness. Multiparameter diagnostics will be used rou-

tinely to assess health status. Network science will be

used to ascertain drug targets, leading to true preventive

medicine.

The emerging bio-inspired automation and au-

tomatic control mechanisms, techniques and mod-

els will continue to offer rich sources of innova-

tion. We will continue to search how the beneﬁts

of systems biology knowledge in living organisms

can help us solve complex, critical problems in in-

creasingly interrelated systems and service infrastruc-

tures.

References

75.1 J. Hasty, D. McMillen, F. Isaacs, J.J. Collins: Com-

putational studies of gene regulatory networks:

In numero molecular biology, Nat. Rev. Genet. 2,

268–279 (2001)

Part H 75