Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

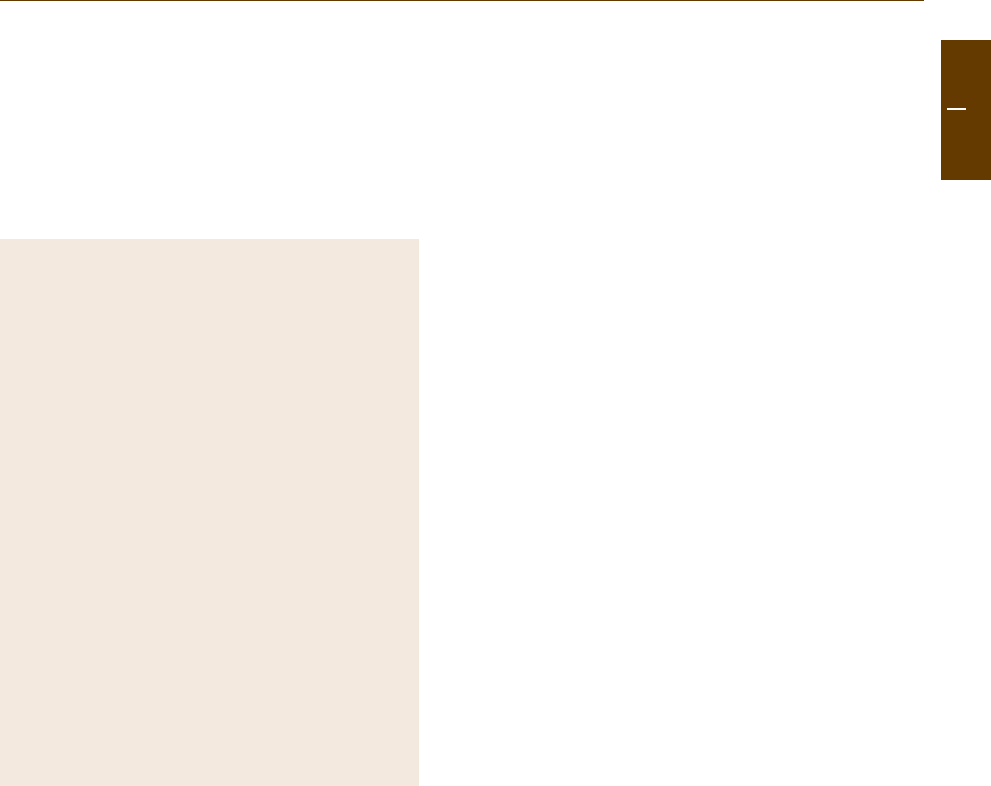
1335

Automatic Co

75. Automatic Control in Systems Biology

Henry Mirsky, Jörg Stelling, Rudiyanto Gunawan, Neda Bagheri, Stephanie R. Taylor, Eric Kwei,

Jason E. Shoemaker, Francis J. Doyle III

The reductionist approaches of molecular and

cellular biology have produced revolutionary

advances in our understanding of biologi-

cal function and information processing. The

difﬁculty associated with relating molecu-

lar components to their systemic function

led to the development of systems biology,

a relatively new ﬁeld that aims to establish

a bridge between molecular level information

and systems level understanding. The novelty

of systems biology lies in the emphasis on

analyzing complexity in networked biological

systems using integrative rather than reduc-

tionist approaches. By its very nature, systems

biology is a highly interdisciplinary ﬁeld that re-

quires the effective collaboration of scientists

and engineers with different technical back-

grounds, and the interdisciplinary training of

students to meet the rapidly evolving needs of

academia, industry, and government. This chap-

ter summarizes state-of-the-art developments of

automatic control in systems biology with sub-

stantial theoretical background and illustrative

examples.

75.1 Basics ..................................................1335

75.1.1 Systems Biology ...........................1336

75.1.2 Control Research in Systems Biology1336

75.2 Biophysical Networks ............................1337

75.2.1 Timing and Rhythm:

Circadian Rhythm Networks

and Oscillatory Processes...............1337

75.2.2 Apoptosis: Programmed Cell Death .1338

75.2.3 Signals in Diabetes:

Insulin Signaling Pathway .............1339

75.3 Network Models

for Structural Classiﬁcation....................1340

75.3.1 Hierarchical Networks...................1341

75.3.2 Boolean Networks, Petri Nets,

and Associated Structures..............1341

75.4 Dynamical Models.................................1342

75.4.1 Stochastic Systems........................1343

75.4.2 Constraints and Optimality

in Modeling Metabolism ...............1344

75.5 Network Identiﬁcation..........................1346

75.5.1 Data-Driven Methods ...................1346

75.5.2 Linear Approximations..................1347

75.5.3 Mechanistic Models, Identiﬁability

and Experimental Design ..............1348

75.6 Quantitative Performance Metrics ..........1349

75.6.1 State-Based Sensitivity Metrics ......1350

75.6.2 Phase-Based Sensitivity Metrics .....1351

75.6.3 Global Versus Local Parameters ......1353

75.7 Bio-inspired Control and Design ............1353

75.8 Emerging Trends ..................................1354

References ..................................................1354

75.1 Basics

Advances in molecular biology over the past two

decades have made it possible to probe experimentally

the causal relationships between processes initiated by

individual molecules within a cell and their macro-

scopic phenotypic effects on cells and organisms.

A systematic approach for analyzing complexity in bio-

physical networks was previously untenable owing to

the lack of suitable measurements and the limitations

imposed in simulating complex mathematical models.

Recent studies provide increasingly detailed insights

into the underlying networks, circuits, and pathways re-

sponsible for the basic functionality and robustness of

Part H 75

1336 Part H Automation in Medical and Healthcare Systems

biological systemsand create new andexciting opportu-

nities for the development of quantitative and predictive

modeling and simulation tools [75.1]. The discipline

of systems biology has emerged in response to the

challenges in modeling and understanding complex bi-

ological networks [75.2,3].

75.1.1 Systems Biology

The ﬁeld of systems biology combines approaches

and methods from systems engineering, computa-

tional biology, statistics, genomics, molecular biology,

biophysics, and other ﬁelds [75.5–7] to help create

systems-level understanding of complex biological net-

works. In particular, systems engineering methods are

ﬁnding unique opportunities in characterizing the rich

dynamic behavior exhibited by biological systems.

Conversely, the new classes of biological problems are

motivating novel developments in theoretical systems

approaches. Two characteristics of systems biology

are [75.4]: (1) integrative view points towards unravel-

ing complex dynamical systems, and (2) tight iterations

between experiments, modeling, and hypothesis gener-

ation (Fig.75.1).

Although the ﬁeld of systems biology is relatively

young, one can already point to early successes in

a number of cases. The work of Arkin on λ-phage was

one of the ﬁrst detailed analyses of a stochastic gene

switch, and showed convincingly that formal stochastic

treatment was requiredto understandthe cell fate switch

between lysis and lysogeny [75.8]. The analysis of per-

fect adaptation in chemotaxis is another example where

multiple groups adopted a systems perspective, and key

insights have been generated [75.9–11]. Notably, the

Experimentation

Experimental

design

Network

identification

Systems modelling

and analysis theory

Fig. 75.1 Systems biology iterations. Interactions between

experimental analysis and theoretical approaches, and the

main tasks for theory at the interfaces (after [75.4])

mechanism for perfect adaptation has been elucidated

and interpreted in classical control engineering terms:

integral feedback [75.11].

The approach of model reduction and systematic

analysis (including requisite modeling assumptions to

yield perfect adaptation) is an excellent example of

an effective systems strategy. This problem continues

to generate new insights, as recent work has shown

that disparate organisms have both overlapping and dis-

tinctive architectures for chemotaxis [75.11]. Another

nice example that has received considerable attention is

the gene network underlying circadian rhythms. Mod-

els have been proposed [75.12], and formal robustness

analysis tools have generated insights on biological de-

sign principles [75.13].

A more detailed case study that might be character-

ized as a success story has also emerged from the work

of Muller et al. on the JAK-STAT pathway [75.14].

They have shown that modeling-experiment iterations

can yield new hypotheses, particularly regarding un-

observable components that can be simulated (but

never measured). One implication, for the JAK-STAT

pathway, involves pharmacological intervention. Cur-

rent practice focuses on the phosphorylation element

of the pathway, but the model shows that a more

effective strategy involves the blocking of nuclear ex-

port.

75.1.2 Control Research in Systems Biology

Natural control systems are paragons of optimality.

Over millennia, these architectures have been honed

to achieve automatic, robust regulation of a myriad

of processes at the levels of genes, proteins, cells,

and entire systems. One of the more challenging

opportunities for systems research is unraveling the

multiscale, hierarchical control that achieves robust per-

formance in the face of stochastic perturbations. These

perturbations arise from both intrinsic sources (e.g., in-

herent variability in the transcription machinery), and

extrinsic sources (e.g., environmental ﬂuctuations). Ro-

bustness in key performance variables to particular

perturbations has been shown to be achieved at the

expense of strong sensitivity (fragility) to other pertur-

bations.

The coexistence of extreme robustness and fragility

constitutes one of the most salient features of highly

evolved or designed complexity [75.15]. Optimally ro-

bust systems are those that balance their robustness to

frequent environmental variations with their coexist-

ing sensitivity to rare events. As a result, robustness

Part H 75.1

Automatic Control in Systems Biology 75.2 Biophysical Networks 1337

and sensitivity analysis are key measures in under-

standing and controlling system performance. Robust

performance reﬂects a relative insensitivity to perturba-

tions; it is the persistence of a system’s characteristic

behavior under perturbations or conditions of uncer-

tainty. Measuring the robustness of a system determines

the behavior (the output or performance) as a function

of the input (the disturbance). Formal sensitivity ana-

lysis allows the investigation of robustness and fragility

properties of mathematical models, yielding local prop-

erties with respect to a particular choice of parameter

values.

Within the ﬁeld of systems engineering, control

engineering has had a pervasive inﬂuence on the disci-

pline of systems biology. For instance, the chemotaxis

work [75.11] was a paradigm of collaboration between

control engineers (Doyle) and biologists (Simon). Other

examples include the robustness analysis of cellular

function [75.15] and the unraveling of design principles

in circadian rhythm [75.13]. There are many other ex-

amples from the control community: for instance, major

advances in understanding signal transduction [75.16],

and the oscillations underlying a positive feedback gene

switch [75.17].

75.2 Biophysical Networks

Biophysical networks are remarkably diverse, cover

a wide spectrum of scales, and are inevitably character-

ized by a range of rich behaviors. The term complexity

is often invoked in the description of biophysical

networks that underlie gene regulation, protein interac-

tions, and metabolic networks in biological organisms.

There are categorically two distinct characterizations

of complexity: (1) the descriptive or topological no-

tion of a large number of constitutive elements with

nontrivial connectivity (described in Sect.75.3), and

(2) the classical notion of behavior associated with

the mathematical properties of chaos and bifurcations

(described in Sect. 75.4). In both biological and more

general contexts, a key implication of complexity is

that the underlying system is difﬁcult to understand and

verify [75.18]. Simple low-order mathematical models

can be constructed that yield chaotic behavior, and, yet,

rich complex biophysical networks may be designed to

reinforce reliable execution of simple tasks or behav-

iors [75.19].

Biophysical networks have attracted a great deal

of attention at the level of gene regulation, where

dozens of input connections may characterize the reg-

ulatory domain of a single gene in a eukaryote, as

well as the protein level, where literally thousands of

interactions have been mapped in so-called protein in-

teractome diagrams that illustrate the potential coupling

of pairs of proteins [75.20, 21]. Similar networks also

exist at higher levels, including the coupling of indi-

vidual cells via signaling molecules, the coupling of

organs via endocrine signaling, and ultimately the cou-

pling of organisms in ecosystems. To elucidate the

mechanisms employed by these networks, biological

experimentation and intuition are by themselves insuf-

ﬁcient. As noted earlier, the ﬁeld of systems biology

has laid claim to this class of problems, and engi-

neers, biologists, physicists, chemists, mathematicians,

and many others have united to embrace these prob-

lems with interdisciplinary approaches [75.22]. In this

ﬁeld, investigators characterize dynamics via mathe-

matical models and apply systems theory with the goal

of guiding further experimentation to better understand

the biological network that gives rise to robust perfor-

mance [75.22].

75.2.1 Timing and Rhythm:

Circadian Rhythm Networks

and Oscillatory Processes

Oscillatory processes are omnipresent in nature, com-

prising the cell cycle, neuron ﬁring, ecological cycles

and others; they govern many organisms’ behaviors.

A well-studied example of a biological oscillator is the

circadian rhythm clock. The term circa- (about) diem

(day) describes a biological event that repeats approx-

imately every 24h. Circadian rhythms are observed at

all cellular levels since oscillations in enzymes and

hormones affect cell function, cell division, and cell

growth [75.23]. They serve to impose internal align-

ments between different biochemical and physiological

oscillations. Their ability to anticipate environmental

changes enables organisms to organize their physiol-

ogy and behavior such that they occur at biologically

advantageous times during the day [75.23]: visual and

mental acuity ﬂuctuate, for instance, affecting complex

behaviors.

The mammalian circadian master clock resides in

the suprachiasmatic nucleus (SCN), located in the

Part H 75.2

1338 Part H Automation in Medical and Healthcare Systems

1°-Phosphorylated

PER:CRY

(PopRo, PopRt,

PtpRo & PtpRT)

1°-Phosphorylated

PER:CRY:Kinase

(PopCRo, PopCRt,

PtpCRo & PtpC)

2°-Phosphorylated

PER:CRY:Kinase

(PoppCRo, &

PoppCRt)

2°-Phosphorylated

PER:CRY

(PoppRo, & PoppRt)

1°-Phosphorylated

PER

(Ponp & Ptnp)

1°-Phosphorylated

PER:Kinase

(PonpCn, PtnpCn)

2°-Phosphorylated

PER:Kinase

(PonppCn)

2°-Phosphorylated

PER:CRY

(Ponpp)

1°-Phosphorylated

PER:CRY

(PonpRon & PonpRtn,

PtnpRon & PtnpRtn)

1°-Phosphorylated

PER:CRY:Kinase

(PonpCnRon, PonpCnRtn,

PtnpCnRon & PtnpCnRtn)

2°-Phosphorylated

PER:CRY:Kinase

(PonppCnRon &

PonppCnRtn)

2°-Phosphorylated

PER:CRY

(PonppRon &

PonppRtn)

2°-Phosphorylated

PER:CRY

(Popp)

2°-Phosphorylated

PER:Kinase

(PoppC)

1°-Phosphorylated

PER:Kinase

(PopC & PtpC)

1°-Phosphorylated

PER

(Pop & Ptp)

PER

(Po & Pt)

PER:Kinase

(PoC & PtC)

CRY

(Ro & Rt)

CRY

(Ron & Rtn)

Degraded

CRY

Degraded PERDegraded PERDegraded PER

Degraded PER

Degraded

per mRNA

(McPo & McPt)

per mRNA

(MnPo & MnPt)

per rev-erb-α cry

cry pre-mRNA

(MnRo & MnRt)

cry mRNA

(McRo & McRt)

Degraded

cry mRNA

Degraded

REV-ERB-A

Degraded

REV-ERB-A dimer

Degraded

REV-ERB-A dimer

Degraded

REV-ERB-A

REV-ERB-A dimer

(RvRv)

REV-ERB-A

(Rv)

only cry1

rev-erb-α

pre-mRNA

(MnRv)

Degraded

rev-erb-α mRNA

(McRv)

REV-ERB-A

(Rvn)

REV-ERB-A dimer

(RvnRvn)

Fig. 75.2 Gene regulatory network underlying circadian rhythms in neurons in the SCN. Activated complexes of proteins inhibit

the transcription of their corresponding genes, thus leading to time-delayed negative feedback and oscillations (after [75.30])

hypothalamus [75.24]. It is a network of multiple

autonomous noisy (sloppy) oscillators, which com-

municate via neuropeptides to synchronize and form

a coherent oscillator [75.25, 26].Atthecoreofthe

clock is a gene regulatory network in which approxi-

mately six key genes are regulated through an elegant

array of time-delayed and coupled negative and pos-

itive feedback circuits (Fig.75.2). The activity states

of the proteins in this network are modulated (acti-

vated/inactivated) through a series of chemical reactions

including phosphorylation and dimerization. These net-

works exist at the subcellular level. Above this layer

is the signaling that leads to a synchronized response

from the population of thousands of clock neurons in

the SCN. Ultimately, this coherent oscillator then co-

ordinates the timing of daily behaviors, such as the

sleep/wake cycle. Left in constant (dark) conditions, the

clock will run freely with a period of only approxi-

mately 24h such that its internal time, or phase, drifts

away from that of its environment. Thus, the ability to

entrain to external time through environmental factors

is vital to a circadian clock [75.27–29].

75.2.2 Apoptosis: Programmed Cell Death

Another example of biophysical networks is the apop-

tosis network in which an extracellular input controls

the response of the cell as a result of this information

processing network. Apoptosis is the programmed cell

death machinery that is used by nature to strategically

kill off unneeded and infected cells, but this mecha-

nism often becomes impaired in cancer cells, leading

to unchecked proliferation.

The speciﬁc example here is triggered by the Fas

ligand. When an activated T-cell contacts a diseased

cell, Fas and its natural ligand bind, resulting in the

formation of the death inducing signalling complex

(DISC). This complex then activates two pathways,

both of which lead to the activation of the so-called

executioner caspase 3. The Fas apoptotic network has

Part H 75.2

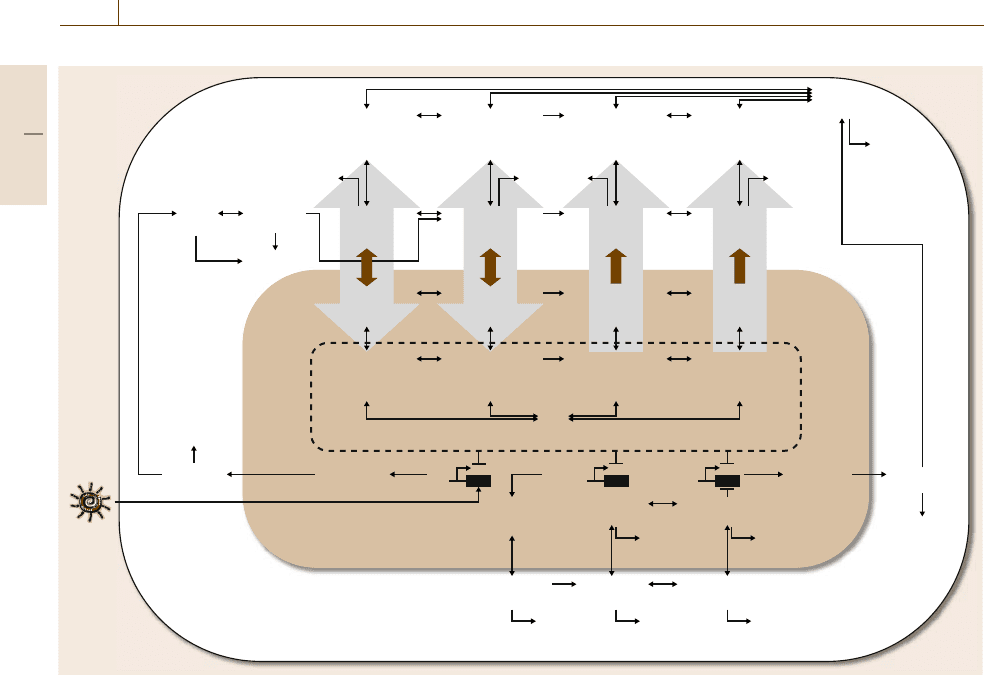
Automatic Control in Systems Biology 75.2 Biophysical Networks 1339

been modeled by [75.31] using ordinary differential

equations and is illustrated in Fig.75.3. In the Type I

pathway, a feedback pathway involving caspase-6 and

caspase-8 regulates the amount of activated caspase-3.

In the Type II pathway, Bcl-2 and active caspase-8 both

interact with the mitochondrial membrane, regulating

mitochondrial permeability. Caspase-8 allows mito-

chondria to become permeable, inducing the activation

of the apoptosome and Smac (second mitochondrial-

activator caspase) [75.32]. The activated apoptosome

(Apopt

active) in turn activates caspase-3, while Smac

can further enhance the activation of the executioner

caspase by removing XIAP (X-linked inhibitor of apop-

tosis protein). FLIP, Bcl-2, and XIAP all antagonize

the apoptotic signal and variations in their quantities

can toggle the apoptotic signal between Type I and

Type II activation or no activation at all. Experimen-

tal evidence has shown that Type I activation requires

a signiﬁcant amount of caspase-8 to be present in the

cell. Yet, in Type II cells, mitochondrial activity ulti-

mately enhances the death signal, signiﬁcantly lowering

the amount of caspase-8 that needs to be activated to

induce apoptosis [75.33].

BCL-2: MitoBCL-2

DISC:FLIP

DISC

DISC:Casp8

Casp8_active Casp8_active:Mito

Casp3_active

Mitochondria

Type II

Type I

Mito_active

Smac_active

Smac_act:XIAP

Apopt_XIAP

Casp3_active:XIAP

Smac

Casp8_active:Casp3

Casp6_active:Casp8

Casp3_active:Casp6

Casp6_active

Casp6

FLIP

Casp8

Casp3

Apopt_active

Apopt_act:Casp3

Apoptosome

XIAP

FasL

Fas

Fig. 75.3 Network schematic of the Type 1 and Type 2 Fas-induced apoptosis network (after [75.31])

Understanding apoptosis in a broader sense will

lead to a better knowledge of the common platform

for emergence of cancer cells, and perhaps point to

possible cures for certain types of cancer. The com-

plexity of apoptosis, however, makes the understanding

very difﬁcult without a systems level approach using

a mathematical representation of the pathway. Further,

analysis of an apoptosis model can reveal the fragility

points in the mechanism of programmed cell death that

can have physiological implications not only for ex-

plaining the emergence of cancer cells but also for

designing drugs or treatment for reinstating apopto-

sis in these cells. A robust performance analysis of an

apoptotic network identiﬁed known network fragilities

as well as new potential targets for therapeutic inter-

vention. Such analyses are crucial to streamlining drug

discovery in highly dynamic networks [75.34].

75.2.3 Signals in Diabetes:

Insulin Signaling Pathway

In healthy cells, the uptake of glucose is regulated by

insulin, which is secreted by β-cells in the pancreas.

Part H 75.2

1340 Part H Automation in Medical and Healthcare Systems

Insulin [x

]

Insulin

P P

Receptor

Receptor [x

]

Receptor [x

]

Insulin

Receptor

IRS1

IRS1 [x

]IRS1 [x

]

GLUT4 [x

] GLUT4 [x

]

Vesicle

Cell

PI3K [x

]IRS1 [x

10a

]

PI(3,4)P

]

PKCζ [x

] PKCζ [x

] Akt [x

]

PI3K

Insulin Insulin

Receptor

Insulin

Receptor

PI(3,4,5)P

] PI(4,5)P

]

Insulin

Receptor

Insulin

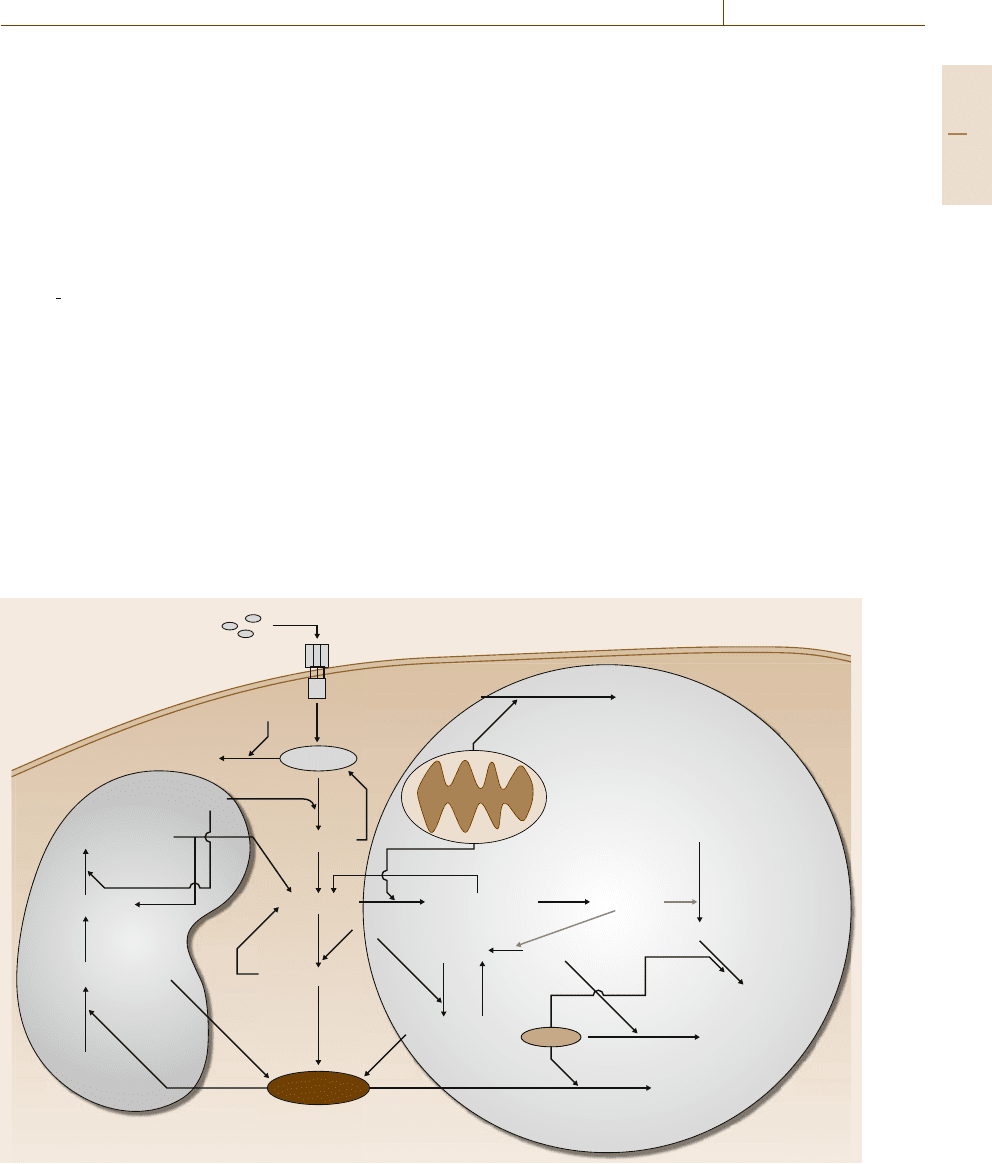
Fig. 75.4 Insulin signalling pathway model (after [75.35])

Simply stated, in patients with type 1 diabetes, the

pancreas does not produce insulin, whereas in type 2

diabetes, among other consequences, the cells are resis-

tant to the insulin produced by the pancreas. The latter

phenomenon is best understood from detailed consid-

eration of the insulin signalling pathway (illustrated in

Fig.75.4). The sequence of actions occurs as follows:

(1) insulin binds to a receptor on the cell surface, which

causes receptor autophosphorylation and activation;

(2) the activated insulin receptor then phosphorylates

insulin receptor substrate-1 (IRS1), which subsequently

forms a complex with phosphatidylinositol-3-kinase

(PI3K); (3) the IRS1-PI3K complex catalyzes the pro-

duction of phosphatidylinositol triphosphate (PIP

which then interacts allosterically with phosinositide-

dependent kinase 1 (PDK

); (4) the PIP

-PDK1 com-

plex phosphorylates protein kinase Akt and protein

kinase C (PKCζ); (5) activated Akt and PKCζ trigger

glucose transporter (GLUT4) translocation from an in-

ternal compartment to the cell membrane. In a healthy

cell, this cascade ultimately leads to uptake of glucose

and helps to regulate glucose levels. In a cell charac-

terized by type 2 diabetes, the cascade is desensitized to

insulin, and the effectivenessof thesignal is diminished.

75.3 Network Models for Structural Classiﬁcation

An important point in systems biology is the integrative

perspective, i.e., the analysis of the system considered

as a whole and across the different levels (gene, pro-

tein, metabolite, etc.) and not the reductionist analysis

Part H 75.3

Automatic Control in Systems Biology 75.3 Network Models for Structural Classiﬁcation 1341

of individual components. While it is useful to catego-

rize the elements and levels of a hierarchical regulatory

scheme, it is more useful to analyze such schemes for

behaviors that emerge from combinations of simpler

motifs. Some simple examples of canonical regulatory

constructs (i. e., motifs) that yield speciﬁc classes of

behavior in gene networks include [75.36]:

1. Positive feedback: multistability, oscillations, state-

dependent response

2. Integral feedback: robust adaptation

3. Negative feedback: steady-state(homeostasis, adap-

tation)

4. Time delay: complex response, oscillations

5. Protein oligomerization: multistability, oscillations,

resonant stimulus frequency response.

In addition, stochastic ﬂuctuations can induce ran-

dom response to stimuli, random outcomes, as well as

stochastic focusing. Such properties are characteristic

of general networks, including social networks, com-

munication networks, and biological networks [75.37].

Given the wide variety of modeling objectives, as well

as the heterogeneous sources of data, it is not surpris-

ing that many approaches exist for capturing network

interactions in the form of mathematical structures.

75.3.1 Hierarchical Networks

Biophysical networks can be decomposed into modular

components that recur across and within given organ-

isms. One hierarchical classiﬁcation is to label the top

level as a network, which is comprised of interacting

regulatory motifs consisting of groups of 2–4 compo-

nents such as proteins or genes [75.38–40]. Motifs are

small subnetworks that are over-represented compared

to random networks with the same large-scale proper-

ties. At the lowest level in this hierarchy is the module

that describes transcriptionalregulation, of which a nice

example is given in [75.41]. At the motif level, one can

use pattern searching techniques to determine the fre-

quency of occurrence of these simple motifs [75.39],

leading to the postulation that these are basic build-

ing blocks in biological networks. Of relevance to the

present discussion is the fact that many of these com-

ponents have direct analogs in systems engineering

architectures. Consider the three dominant network mo-

tifs found in Escherichia coli [75.39]:

1. Coherent feedforward loop: in this, one transcrip-

tion factor regulates another factor, and, in turn, the

pair jointly regulates a third transcription factor

2. Single input module (SIM): in systems terminology,

a single-input multiple output block architecture

3. Densely overlapping regulons: in systems termi-

nology, a multiple-input multiple output block

architecture.

Similar studies in a completely different organism,

Saccharomyces cerevisiae, yielded six related or over-

lapping network motifs [75.38]:

1. Autoregulatory motif: negative feedback in which

a regulator binds to the promotor region of its own

gene

2. Feedforward loop: as described earlier

3. Multicomponent loop: effectively, a closed-loop

with two or more transcription factors

4. Regulator chain: a cascade of serial transcription

factor interactions

5. Single input module: as described earlier (SIM)

6. Multiinput module: a natural extension of the pre-

ceding motif.

In effect, these studies provide strong evidence that,

in both eukaryotic and prokaryotic systems, cell func-

tion is controlled by sophisticated networks of control

loops that are cascading onto and interconnected with

other (transcriptional) control loops. The noteworthy

insight is that the complex networks, which underlie bi-

ological regulation, appear to be made of elementary

systems components like a digital circuit. This lends

credibility to the notion that analysis tools from sys-

tems engineering should ﬁnd relevance in this problem

domain.

75.3.2 Boolean Networks, Petri Nets,

and Associated Structures

Boolean networks are abstract mathematical models

employed for coarse-grained analysis of biophysical

networks. A Boolean network is represented as a graph

of nodes,with directededges between nodes and a func-

tion for each node (e.g., [75.42]). Boolean networks

are used to model network dynamics; for instance,

a Boolean network can be used to model transcripts and

proteins:

DNA mRNA

t+1

DNA

t+1

Fig. 75.5 Transcription of transcripts (mRNA)

Part H 75.3

1342 Part H Automation in Medical and Healthcare Systems

mRNA Protein

t+1t

Fig. 75.6 Translation from transcripts to proteins

1. Transcripts and proteins are either on (1) or off (0).

2. The expression of a node at time step t is given by

a logical rule of the expression of its effectors at

time t −1.

3. Transcription depends on transcription factors; re-

pressors are dominant (Fig.75.5).

4. Translation depends on the presence of the tran-

script (Fig.75.6).

5. Transcripts and proteins decay in one step if not

produced.

Place/transition (P/T) nets, or Petri nets, introduced

by Carl Adam Petri in 1962, have been intensively stud-

ied as one of several formal methods used to verify the

correctness of systems, which are described as mathe-

matical objects that can handle characteristics such as

nondeterminism and concurrency (e.g., [75.43]).

There are several additional types of networks

such as Bayesian nets, which combine directed acyclic

graphs with a conditional distribution for each random

variable (vertices in a graph, e.g., [75.44]), and signed

directed graphs, in which a signed directed edge is used

to represent activation versus inhibition (depending on

the sign, e.g., [75.45]). Alternatively, S-systems (bio-

chemical systems theory, BST) provide an approach

wherein polynomial nonlinear dynamic nodes are used

to capture network behavior (e.g., [75.46]).

75.4 Dynamical Models

While the consideration of motifsand network topology

is essential for unraveling design principles in com-

plex biophysical networks, it is necessary to understand

the role of dynamic behavior in ascribing meaning to

the rich hierarchies of regulation. Moreover, because

of the interplay between topology and dynamics, it is

often not enough in systems biology to specify only

the nodes (components) and edges (interactions). The

robust control of biophysical networks requires the an-

swer to many challenging questions such as: (1) What

are the dynamical aspects of the interaction? (2) What is

the characteristic quantity changed by the interaction?

Some of the intrinsically dynamic features of bio-

physical networks have been analyzed in a recent paper

that shows the close relationshipbetween dynamicmea-

sures of robustness and the abundance of particular

network motifs for a wide range of organisms [75.47].

Attempts to detail dynamic behavior in these networks

have fallen into three broad classes of modeling tech-

niques: (1) ﬁrst-principles approaches, (2) empirical

model identiﬁcation, and (3) a hybrid approach that

combines minimum biophysical network knowledge

with an objective function to yield a predictive model.

In this section, we outline some key results in the de-

velopment of mechanistic models, and in the following

section, we will address network identiﬁcation.

Given detailed knowledge of a biological archi-

tecture, mathematical models can be constructed to

describe the behavior of interconnected motifs or tran-

scriptional units (TUs). A number of excellent review

papers have been published in recent years [75.1,36,48,

49]. In the majority of these studies, gene expression

is described as a continuous-time biochemical process,

using combinations of algebraic and ordinary differ-

ential equations (ODEs) [75.12, 36, 50]. In a similar

manner, models at the signal transduction pathway level

have been developed in a continuous-time framework,

yielding ODEs [75.51]. At the TU level, a detailed

mathematical treatment of transcriptional regulation is

described in [75.41]. Mechanistic models for a number

of speciﬁc biological systems have been reported, in-

cluding basic operons and regulons in E. coli (trp, lac,

and pho) and bacteriophage systems (T7 and λ) [75.52].

Systems theory has found an enabling role in

the analysis of the complex mathematical structures

that result from the previously described modeling

approaches. The language of systems theory now

dominates the quantitative characterization of biolog-

ical regulation, as robustness, complexity, modularity,

feedback, and fragility are invoked to describe these

systems. Even classical control theoretic results, such

as the Bode sensitivity integral, are being applied to

describe the inherent tradeoffs in sensitivity across fre-

quency [75.53]. Robustness has been introduced as

both a biological system-speciﬁc attribute, as well as

a measure of model validity [75.54, 55]. In the next

section, brief accounts of systems-theoretic analysis of

biological regulatory structures are given, emphasizing

where new insights into biological regulation have been

uncovered.

Part H 75.4

Automatic Control in Systems Biology 75.4 Dynamical Models 1343

75.4.1 Stochastic Systems

Discrete stochastic modeling has recently gained

popularity owing to its relevance in biological pro-

cesses [75.8, 56–59] that achieve their functions with

low copy numbers of some key chemical species. Un-

like the solutions to stochastic differential equations,

the states/outputs of discrete stochastic systems evolve

according to discrete jump Markov processes, which

naturally lead to a probabilistic description of the sys-

tem dynamics. A ﬁrst-order Markov process is a random

process in which the future probabilities are dependent

only on the present value, and not on past values. Such

descriptions canﬁnd relevance in systems biologywhen

the magnitude of the ﬂuctuations in a stochastic system

approaches the levels of the actual variables (e.g., pro-

tein concentrations). In addition, there are qualitative

phenomena that are intrinsic to such descriptions that

arise in biological systems, as will be mentioned later.

The idea that stochastic phenomena are essential for

understanding complex transcriptional processes was

nicely illustrated by Arkin and coworkers in the analy-

sis of the phage λ lysis–lysogenydecision circuit [75.8].

The probabilistic division of the initially homogeneous

cell population into subpopulations corresponding to

the two possible fate outcomes was shown to require

a stochastic description (and could not be described

with a continuous deterministic model). In particular,

the coexistence of the two subpopulations necessi-

tated such a formal characterization, and the relative

sensitivity of the subpopulations to model parameters

including external variables could be analyzed with

the resulting models. In a more recent work, Samilov

and coworkers [75.60] have shown another example

of a biological behavior that is intrinsically stochastic

in nature – namely the dynamic switching behavior in

a class of biochemical reactions (enzymatic futile cy-

cles). In this case, the behavior is more subtle than the

lysis–lysogeny switch, where the existence of a bifurca-

tion was at least evident in the continuous differential

equation model. In the enzymatic futile cycle prob-

lem, the deterministic model gives no indication of

multiplicity, yet the discrete stochastic model generates

behaviors, including switching as well as oscillations,

that indicate characteristics of bifurcation regimes. It is

suggested that such noise-induced mechanisms may be

responsible for control of switch and cycle behavior in

regulatory networks.

In the discrete stochastic setting, the states and out-

puts are random variables governed by a probability

density function, whichfollows a chemicalmaster equa-

tion (CME) [75.61]. The rate of reaction no longer

describes the amount of chemical species being pro-

duced or consumed per unit time in a reaction but

rather the likelihood of a certain reaction to occur

in a time window. Though analytical solution of the

CME is rarely available, the density function can be

constructed using the stochastic simulation algorithm

(SSA) [75.61].

The discrete stochastic system of interest is de-

scribed by a CME [75.62]

d f(x, t|x

, t

)



k=1

(x−v

, p) f(x−v

, t|x

, t

)

−a

(x, p) f(x, t|x

, t

) , (75.1)

where f(x, t|x

, t

) is the conditional probability of the

system to be at state x and time t, given theinitial condi-

tion x

at time t

. The state vector x gives the molecular

counts of the species in the system. Here, a

denotes

the propensity functions, v

denotes the stoichiomet-

ric change in x when the k-th reaction occurs and m is

the total number of reactions. The propensity function

(x, p)dt gives the probability of the k-th reaction to

occur between time t and t + dt, given the parame-

ters p. As the state values are typically unbounded,

the CME essentially consists of an inﬁnite number of

ODEs, whose analytical solution is rarely available ex-

cept for a few simple problems. The SSA provides an

efﬁcient numerical algorithm for constructing the den-

sity function [75.61]. The algorithm follows a Monte

Carlo approach based on the joint probability for the

time to and the index of the next reaction, which is

a function of the propensities. The SSA indirectly sim-

ulates the CME by generating many realizations of the

states (typically of the order of 10

) at speciﬁed time t,

given the initial condition and model parameters, from

which the distribution f (x, t|x

, t

) can be constructed.

There has been simultaneous advancement in ex-

perimental methods for quantifying the characteristics

of biological noise [75.63–65] along with advances in

computing and simulation. Anumber of groups have re-

cently useddual reportermethods totrack the activity of

identical genes in the same cell to measure the impact of

noise on expression. In the work of Elowitz and cowork-

ers, the separate effects of stochastic behavior in the

transcriptional and translational processes in prokary-

otes (so-called intrinsic noise) are distinguished from

noise effects arising fromother cellularcomponents that

inﬂuence therate of gene expression (so-called extrinsic

noise [75.63,65]). Raser and O’Shea analyze eukaryotic

systems with both cis-acting and trans-acting mutations

Part H 75.4

1344 Part H Automation in Medical and Healthcare Systems

to distinguish between the noise effects that are intrin-

sic to transcription as opposed to upstream processes

that might ultimately inﬂuence expression [75.64].

The interface of discrete stochastic systems and

biology has clearly led to new insights into stochas-

tic phenomena in biological systems, and has also

spurred the development of more efﬁcient computa-

tional methods for stochastic simulation, as well as

analysis methods for these models. This interface will

continue to motivate developments in systems engi-

neering, with improved methods for imaging biological

systems that include the ability to resolve spatial

behaviors. Distributed stochastic models will require

more sophisticated algorithmic developments, particu-

larly as one builds models to truly address systems-scale

phenomena.

75.4.2 Constraints and Optimality

in Modeling Metabolism

To understand complex biological systems, instead of

starting from actual implementations and observations,

one can reduce the problem by ﬁrst separating the

possible from the impossible, such as conﬁgurations

and behaviors that would violate constraints. Systems

approaches try to exploit three broad classes of con-

straints:

1. Empirical: large-scale experimental analysis can

provide constraints on possible network structures,

such as the average or maximal number of interac-

tions per component.

2. Physico-chemical: laws qof physics such as conser-

vation of mass and thermodynamics impose con-

straints on cellular and network behaviors. These

are used, in particular, for structural network ana-

lysis (SNA) with roots in the analysis of chemical

reaction networks [75.66].

3. Functional: biological systems perform certain

functions and their building blocks are conﬁned to

a large, yet ﬁnite set. Network structures and behav-

iors have to conform with both aspects.

Functional constraints constitute the main differ-

ences betweencomplex physics and biology. In physics,

they do not exist. Biological (as well as engineered)

systems evolve to fulﬁll functions, and are constantly

evaluated for their performance. Insufﬁcient perfor-

mance will lead to extinction, and better solutions are

likely to survive. Hence,it is reasonable to assume some

kind of optimality in biological systems. The immediate

consequence of a purpose is a considerably smaller de-

sign space, in which effective and reliable network are

rare and presumably highly structured. Understanding

complexity in biology could, thus, employ a calculus of

purpose – by asking teleological questions such as why

cellular networks are organized as observed, given their

known or assumed function [75.67].

Physico-chemical Constraints in Metabolism

Essential constraints for the operation of metabolic net-

works are imposed by (1) reaction stoichiometries, (2)

thermodynamics that restrict ﬂow directions through

enzymatic reactions,and (3)maximal ﬂuxes forindivid-

ual reactions. For instance, metabolism usually involves

fast reactions and high turnover of substances when

compared with regulatory events. Therefore, on longer

time-scales, it can be regarded as being in quasi-steady

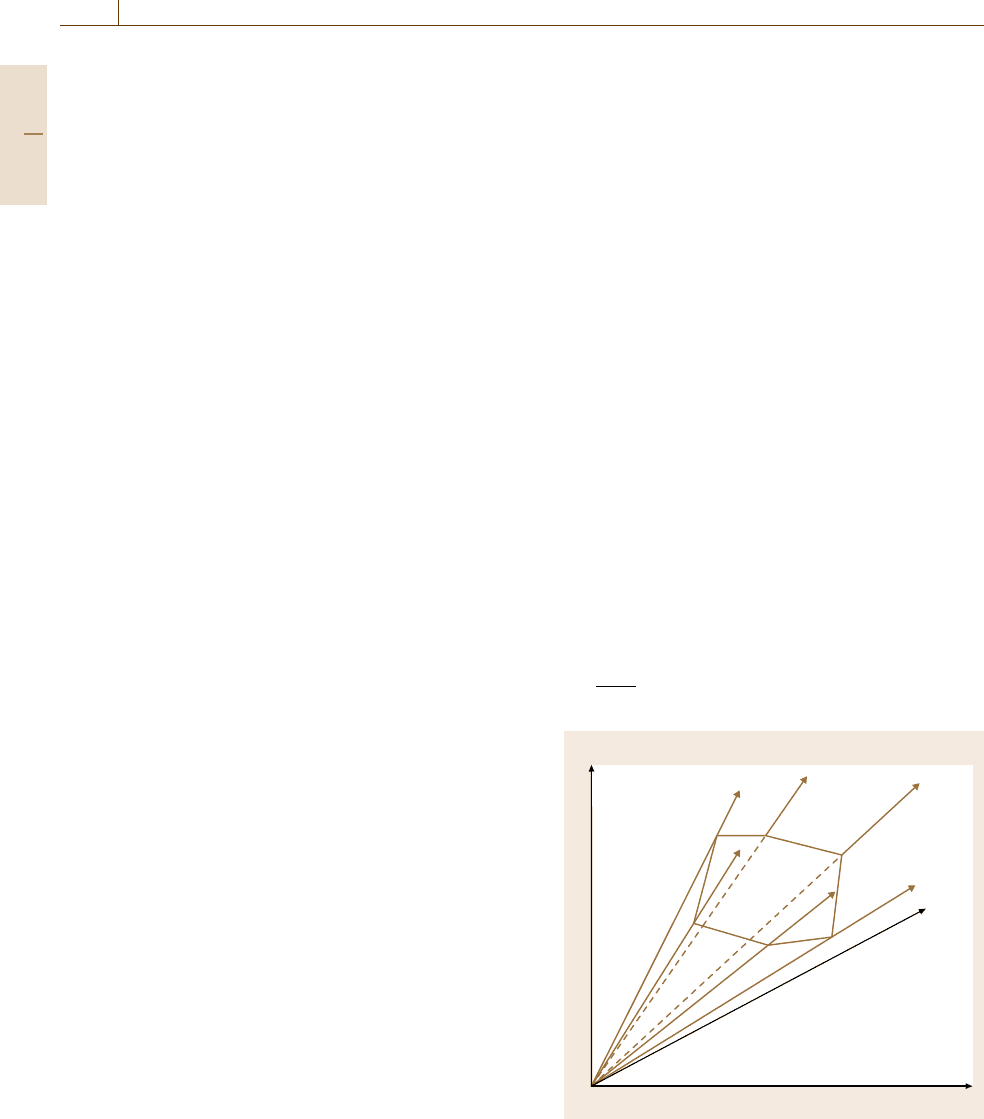
state. The metabolite balancing equation (75.2)for

a system of m internal metabolites and q reactions with

the m×q stoichiometric matrix N and the q×1 vector of

reaction rates (ﬂuxes) r formalizes this main constraint

in SNA. As for most real networks q * m, the system

of linear equation (75.2) is underdetermined. However,

all possible solutions are contained in a convex vector

space, or ﬂux cone (Fig.75.7). Methods from convex

analysis allow to investigate this space [75.68,69]

dx(t)

=N·r =0 .

(75.2)

Rate 2

Rate 1

Rate 3

Fig. 75.7 Linear constraints specify a ﬂux cone, with path-

ways as generating rays, projection on three-dimensional

ﬂux space (after [75.4])

Part H 75.4