Никуличева Н.Г. и др. Метрологическое обеспечение и контроль качества материалов и изделий
Подождите немного. Документ загружается.


41
Основной их них является полная динамическая характеристика,
полностью описывающая принятую математическую модель динамических
свойств СИ. В качестве нее используют: дифференциальные уравнения;
переходную, импульсную переходную, амплитудно-фазовую и амплитудно-
частотную характеристики; совокупность амплитудно-частотной и
фазочастотной характеристик; передаточную функцию.
Дифференциальные уравнения наиболее полно описывают динамические
свойства СИ. Общий вид уравнения с нулевыми начальными условиями:
(
)
(
)
( )
(
)
(
)
( )
tXK
dt
tXd
K
dn
tXd
KtY
dt
tYd
b
dt
tYd
b
n
n
n
n
n
n
m
m
m
m
m
m 0
1
1
1
1
1
1
+⋅⋅⋅++=+⋅⋅⋅++
−
−
−
−
−
−
, (1.14)
где b
i
, K
i
— постоянные коэффициенты.
В подавляющем большинстве случаев оно может быть приведено к
уравнению:
(
)
(
)
( ) ( )
tXKtY
dt
tYd
b
dt
tYd
b
m
m
m
m
m
m 0
1
1
1
=+⋅⋅⋅++
−
−
−
. (1.15)
Его решение Y(t) описывает выходной сигнал средства измерений при
входном сигнале X(t). Данное уравнение отличается от (1.14) присутствием
членов, содержащих произведения коэффициентов b и высших производных от
Y(t), которые и описывают динамические свойства СИ. При их равенстве нулю
уравнение (1.16) переходит в (1.15).
Порядок уравнения (1.16) бывает довольно высоким, по крайней мере,
выше второго. Его решение даже при известном виде функции Y(t) весьма
затруднено. Кроме того, неизвестно аналитическое выражение для Y(t) и
определение производных невозможно. Дифференциальные уравнения
высокого порядка могут быть представлены системой дифференциальных
уравнений первого и второго порядков. Это, по существу, означает
представление сложного в динамическом смысле СИ совокупностью более
простых, хорошо изученных динамических элементов (нулевого, первого и
второго порядков).
Элемент нулевого порядка описывается уравнением (1.15), динамический
элемент первого порядка — уравнением:

42
(
)
( ) ( )
tXKtY
dt
tdY
T
0
=+
, (1.16)
где Т - постоянная времени. Вместо нее применяют и величину ω
г
=1/Т,
называемую граничной частотой.
Динамический элемент второго порядка описывается уравнением:
(
)
(
)
( ) ( )
tXKtY
dt
tdY
dt
tYd
0
0
2
2
2
0
21
=++
ω
β
ω
, (1.17)
где ω
0
— частота собственных колебаний; β — коэффициент
ддемпфирования, или степень успокоения.
Переходная характеристика h(t) — это временная характеристика СИ,
полученная в результате подачи на его вход сигнала в виде единичной функции
заданной амплитуды X(t) = Xm • l(t). Она описывает инерционность СИ,
обуславливающую запаздывание и искажение выходного сигнала относительно
входного. Переходную характеристику находят либо опытным путем, либо
решая соответствующее дифференциальное уравнение при X(t) = X
m
• l(t).
Импульсная переходная характеристика g(t) - это временная
характеристика СИ, полученная в результате приложения к его входу сигнала в
виде дельта - функции.
Переходная и импульсная характеристики связаны между собой:
( ) ( )
∫
=
t
dttgth
0
. (1.18)
Как и дифференциальное уравнение, эти характеристики в полной мере
определяют динамические свойства СИ. Выходной сигнал при известном
входном X(t) определяют с помощью интеграла Дюамеля:
( ) ( ) ( )
τττ
dtgXtY
t
−=
∫
0
или
( ) ( ) ( )
∫
−=
t
dthX
dt
d
tY
0
τττ
. (1.19)
Переходная и импульсная характеристики элементов первого порядка:
( )
−=
−
T
t
m
eKXth 1
0
,
( )
T
t
m
e
T
KX
tg
−
=
0
. (1.20)

43
Их графики приведены на рисунке 1.4. Там же показан графический
способ определения постоянных времени T путем проведения касательных к
точке начала процесса. Часто для оценки длительности переходного периода
определяют время установления t
y
(см. рисунок 1.4).
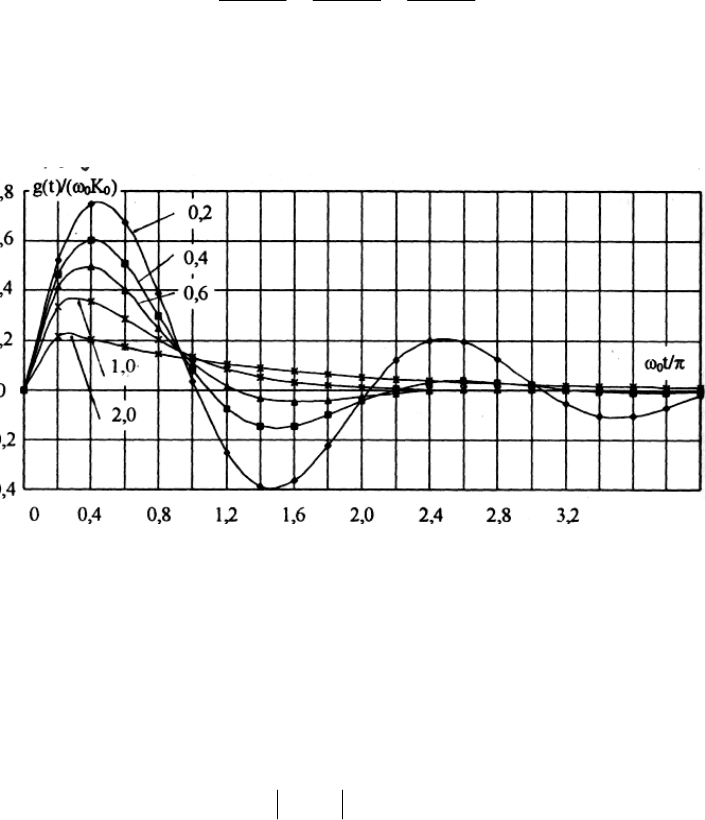
Для динамического элемента второго порядка вид характеристик h(t) и
g(t) зависит от коэффициента демпфирования (рисунки 1.5 и 1.6). Имеют место
три режима (считается, что X
m
=1):
• колебательный при β<1
( )
( )
+−
−
−=
−
βωβ
β
βω
arccos1sin
1
1
0
2
2
0
0
t
e
Kth
t
, (1.21)
( )
t
eK
tg
t
0
2
2
00
1sin
1
0
ωβ
β
ω
βω
−
−
=
−
, (1.22)
Рис. 1.4 Переходная и импульсная переходная характеристики динамических
элементов первого разряда
• критический при β = 1
(
)
(
)
[
]
t
etKth
0
00
11
ω
ω
−
+−=
,
(
)
t
teKtg
0
2
00
ω
ω
−
=
, (1.23)
• апериодический при β > 1
( )
( )
+−
−
−=
−
ββω
β
βω
archtsh
e
Kth
t
1
1
1
2
0
2
0
0
,
( )
(
)
1
1
2
0
2
00
0
−
−
=
−
βω
β
ω
βω
tsh
eK
tg
t
. (1.24)
44
Критический режим является граничным между колебательным и
апериодическим. Он характерен тем, что переходный процесс наиболее быстро
стремится к установившемуся значению.
(
)
(
)
(
)
(
)
tj
m
tj
m
eYeYjY
ωωϕω
ωω
==
+
. (1.25)
K частотным характеристикам относятся амплитудно-фазовая G(jω),
амплитудно-частотная A(ω) и фазочастотная φ(ω) характеристики. Частотные
методы анализа основаны на исследовании прохождения гармонических
колебаний различных час тот через СИ. Если на вход линейного СИ подать
входной сигнал X(jω)=X
m
(ω)e
jωt
, то выходной сигнал можно записать в виде:
Амплитудно-фазовой характеристикой называют отношение :
( )
(
)
( )
(
)
( )
(
)
( )
( )
ωϕ
ω
ω
ω
ω
ω
ω
ω
j
m
m
m
m
e
X
Y
X
Y
jX
jY
jG ===
. (1.26)
Она описывает изменение показаний СИ при изменении частоты
входного сигнала и характеризует только установившийся режим его работы.
Рис. 1.5 Импульсная переходная характеристика динамического элемента
второго порядка при различных значениях коэффициента демпфирования
B практике измерений получила большое распространение амплитудно-
частотная характеристика (АЧХ):
(
)
(
)
(
)
(
)
ωωωω
mm
XyjGA /==
, (1.27)
45
представляющая собой зависящее от круговой частоты отношение амплитуды
выходного сигнала линейного СИ в установившемся режиме к амплитуде
входного синусоидального сигнала.
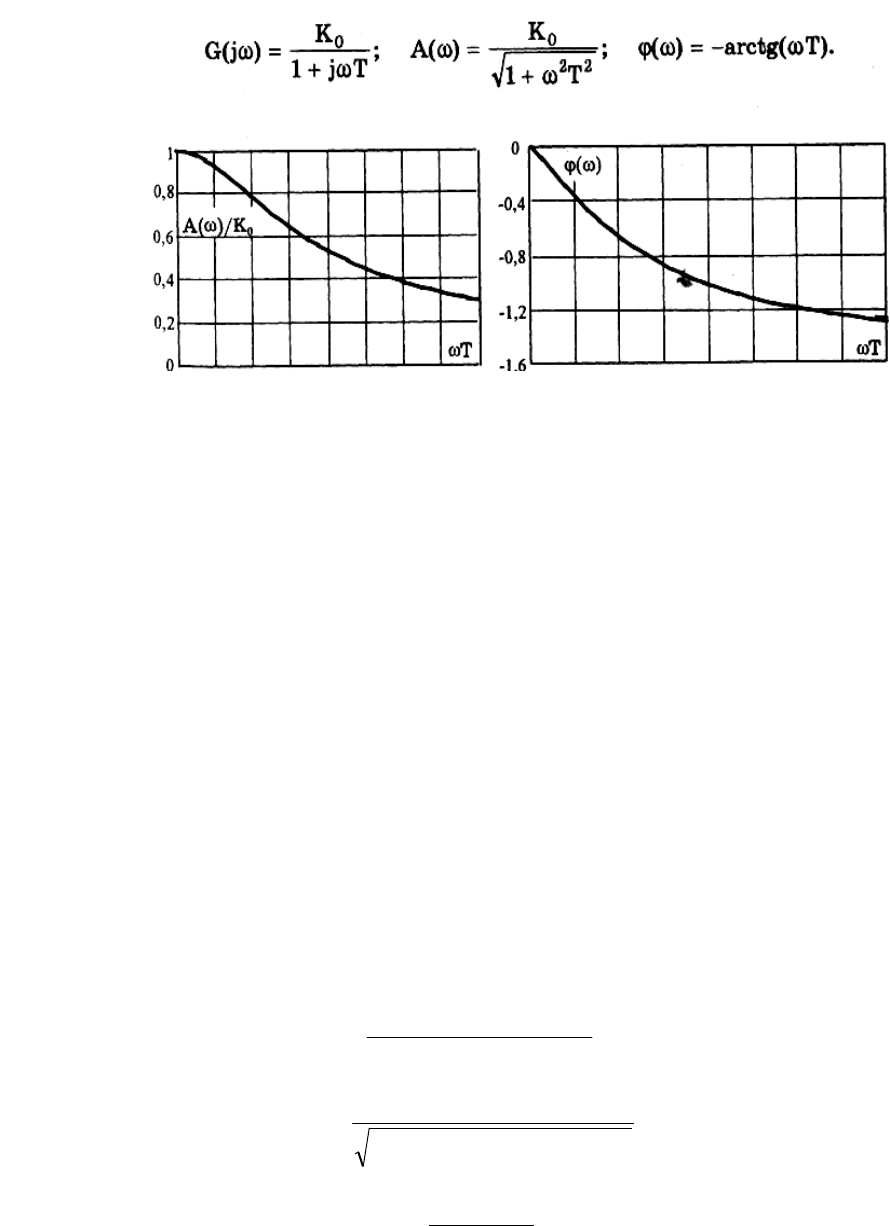
Рис. 1.6 Амплитудно-частотная (а) и фазочастотная (б) характеристики
динамического элемента первого порядка.
Фазочастотная характеристика (ФЧХ) φ(ω) — это зависящая от
частоты разность фаз между выходным сигналом и входным синусоидальным
сигналом линейного СИ в установившемся режиме.
Идеальный безынерционный элемент, описываемый уравнением (1.28),
имеет следующие частотные характеристики: G(jω) = K
0
, Α(ω) = K
0
, φ(ω) = 0.
Для элемента первого порядка (рис. 1.6), задаваемого уравнением:
Динамический элемент второго порядка имеет следующие частотные
характеристики:
( )
0
2
0
2
0
/2/1
ωβωωω
ω
j
K
jG
+−
=
, (1.28)
( )
( )
2
0
22
2
2
0
2
0
/4/1
ωωβωω
ω
+−
=
K
A
, (1.29)
( )
−
−=
2
0
2
0
/1
/2
ωω
ωβω
ωϕ
arctg
. (1.30)
O 0,4 0,8 1,2 1,6 2 2,4 2,8 3,2

46
Для него вид частотных характеристик существенно зависит от
коэффициента демпфирования β (рисунок 1.7). При β = O,6...0,7 в
относительно широком диапазоне частот Α(ω) » K
0
. Этот режим важен для
многих практических применений таких элементов. При β < 0,6 наблюдаются
резонансные явления для частот, близких к ω
0
.
O 0,4 0,8 1,2 1,6 2 ω⁄ω
0
Рис. 1.7 Амплитудно-частотная и фазочастотная характеристики
динамического элемента второго порядка
Ясная физическая интерпретация и относительная простота
экспериментального определения послужили причиной широкого применения
частотных характеристик в метрологии.
Частотные характеристики СИ связаны с другими его динамическими
характеристиками следующими соотношениями:
( ) ( )
∫
∞
−
=
0
dtetgjG
tj
ω
ω
;
( ) ( )
∫
∞
∞−
=
ωω
π
ω
dejGtg
tj
2
1
. (1.31)
47
Рассмотрим типичную для электронного вольтметра и аналогового
осциллографа АЧХ. Если вольтметр предназначен для измерения и
постоянного и переменного напряжения (а осциллограф работает при
"открытом" входе), то АЧХ начинается с нулевой частоты и продолжается до
некоторой граничной частоты ω
гр
, после которой происходит ее существенный
спад. У вольтметров переменного тока и осциллографов с "закрытым" входом
АЧХ при нулевой частоте равна нулю, а затем с ростом частоты достигает
ycтановившегося значения Α
m.
Соответствующий граничной частоте ω
гр
уровень kA
m
(k < 1), до которого
спад АЧХ считается допустимым, у различных устройств задается по-разному.
Характер изменения зависимости A(ω) при частотах, больших граничной ω
гр
,
также существенно зависит от технической реализации СИ.
Полоса частот ∆ω
1
(или ∆ω
2
), в которой АЧХ средства измерений
изменяется не более чем на наперед заданную величину, называется его
полосой пропускания. Она является важной частной динамической
характеристикой СИ. Часто вместо полосы пропускания указывают начальную
ω
н
и граничную ω
гр
частоты. Так, для электронного аналогового вольтметра
переменного тока марки B3-38Б полоса частот простирается от 20 Гц до 5 МГц.
Для широкополосного осциллографа марки Cl-108 полоса пропускания
составляет 350 МГц.
Передаточная функция G(p) — это отношение преобразования Лапласа
выходного сигнала СИ к преобразованию входного сигнала при нулевых
начальных условиях. Уравнение можно записать в виде:
(
)
(
)
(
)
pXKpYpbpbpb
m
m
m
m 01
1
1
1 =+⋅⋅⋅++
−
−
, (1.32)
где X(p), Y(p) - изображения по Лапласу входного и выходного сигналов
СИ.
Их отношение является передаточной функцией:
(
)
(
)
(
)
(
)
1//
1
1
10
+++==
−
−
pbpbpbKpXpYpG
m
m
m
m
L
. (1.33)
48
Идеальный безынерционный элемент имеет передаточную
характеристику G(р)=К
0
; элемент первого порядка - G(p)=K
0
/(Tp+l); элемент
второго порядка - G(p) = K
0
/( р
2
/ω
2
0
+ + 2β ρ/ω
0
+1).
Кроме полных характеристик часто используются частные,
представляющие собой функционал или параметр полной динамической
характеристики. K ним относятся: время реакции, неравномерность АЧХ, время
нарастания переходной характеристики и ряд других .
При рассмотрении данных характеристик необходимо учитывать и
характеристики чувствительности средств измерений к влияющим величинам.
1.5.3 Характеристики чувствительности средств измерений к
влияющим величинам
Влияние, оказываемое внешними факторами, может быть описано, если
известны следующие характеристики:
Функция влияния Ψ(ξ) — это зависимость изменения метрологической
характеристики средства измерений от изменения влияющей величины или
их совокупности в рабочих условиях применения СИ.
Изменения значений метрологических характеристик средств измерений,
вызванные изменениями влияющих величин в установленных пределах, ε(ξ)
— это разность (без учета знака) между метрологическими
характеристиками, соответствующей некоторому заданному значению
влияющей величины ξ в пределах рабочих условий применения средств
измерений, и этой же метрологической характеристики, соответствующей
нормальному значению влияющей величины.
Неинформативные параметры выходного сигнала являются одним из
видов влияющих величин и определяют допустимую область значений тех
параметров выходного сигнала, которые не содержат непосредственной
информации о значении измеряемой величины. Однако они определяют
возможность нормальной работы средств измерений.
49
Дополнительная погрешность средств измерений вызывается
изменениями влияющих величин относительно своих нормальных значений и,
следовательно, является их функцией.
Функции влияния могут нормироваться как отдельно для каждой
влияющей величины, так и для определенной их совокупности. Нормирование
совместных функций целесообразно и необходимо в тех случаях, когда
существенны эффекты взаимовлияния величины на характеристики
погрешностей.
Влияющие величины могут вызывать изменения не только погрешности,
но и других метрологических средств измерений. Поэтому для таких случаев
целесообразно предусмотреть нормирование соответствующих функций
влияния.
Функция Ψ(ξ) устанавливает связь между статистическими
характеристиками дополнительной погрешности ∆
с
средства измерения и
изменением влияющей величины: ∆ξ=ξ-ξ
0
, где ξ и ξ
0
— текущее значение
влияющей величины в реальных условиях применения средств измерений и ее
нормированное значение соответственно. Математическое ожидание
(систематическая составляющая) и среднеквадратическое отклонение (СКО)
Дополнительной погрешности имеют вид: М[∆
с
]=Ψ
∆s
(ξ); σ[∆
с
]= Ψ
σ
(ξ), где Ψ
∆s
(ξ)
и Ψ
σ
(ξ) — функции влияния величины ξ на систематическую погрешность и
СКО случайной погрешности средств измерений. При необходимости функция
влияния на вариацию нормируется отдельно. В этом случае характеристики
погрешности конкретного средства измерений выражаются следующим
образом (для простоты считается, что вариация равна нулю):
М[∆] = ∆
0S
+ Ψ
∆s
(ξ); σ[∆] = σ[
0
о
∆ ] + Ψ
σ
(ξ). (1.34)
Указанные формулы справедливы в том случае, когда изменения
влияющих величин ∆ξ являются известными детерминированными функциями.
Если же ∆ξ учитываются как случайные величины или функции, обладающие
своими математическими ожиданиями и дисперсиями, то:

50
М[∆] = ∆
0S
+ Ψ
∆s
(ξ); σ[∆] =
( ) ( )
[ ]
ξξσ
σ
S
о
D
∆
Ψ+
Ψ+
∆
2
0
.
(1.35)
Это особенно важно для функции Ψ
∆s
(ξ), поскольку влияющие величины
обычно вызывают значительные изменения именно систематической
погрешности. В данном случае функция влияния Ψ
∆s
(ξ) характеризуется своим
математическим ожиданием М [Ψ
∆s
(ξ)] и дисперсией D [Ψ
∆s
(ξ)].
Учет влияния случайного разброса величин ∆ξ на дисперсию или СКО
путем введения соответствующих функций Ψ
D
(ξ) и Ψ
σ
(ξ) привел бы к тому, что
их необходимо было бы учитывать как случайные величины. И поэтому сама
случайная погрешность средств измерений должна была бы рассматриваться
как случайная функция с очень сложным видом нестационарности. Все это
привело бы к практически непреодолимым трудностям при оценке
погрешностей. В то же время значения ∆ξ влияют на характеристики случайной
погрешности значительно меньше, чем на систематическую погрешность. Это
дает основание пренебречь влиянием разброса величин ∆ξ на дисперсию
случайной погрешности и рассматривать функции влияния Ψ
D
(ξ) и Ψ
σ
(ξ) как
детерминированные. При проведении расчетов рекомендуется учитывать
только те значения аргументов ∆ξ при которых указанные функции влияния
имеют максимальные значения — Ψ
D
(ξ)
max
.
Для функции влияния нормируются ее вид и параметры. Характеристики
аргумента ∆ξ, при расчетах определяются исходя из реальных условий
эксплуатации средств измерений. При этом знания только предельных
значений ∆ξ недостаточно, нужно иметь информацию, как о центре
группирования, так и о степени ее разброса.
Наиболее просто дополнительные погрешности рассчитываются для
средств измерений, у которых функции влияния различных внешних величин
взаимно независимы. Каждое средство измерений имеет свой класс точности.
Класс точности — это обобщенная метрологическая характеристика,
определяющая различные свойства средств измерений. Класс точности средств
