Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 2
Подождите немного. Документ загружается.

51
Îñòàâøàÿñÿ ãðóïïà ýëåìåíòîâ âûäåëÿåòñÿ âî âòîðè÷íóþ ìàòðèöó, õà-
ðàêòåðèñòèêè êîòîðîé îïðåäåëÿþòñÿ ïî ñëåäóþùèì çàâèñèìîñòÿì:
N
2
=N-n, x
i
(2)
=x
i
, y
i
(2)
=y
i
-n, M
2
=M-nN, i=n+1,n+2,...,N. (6.76)
Åñëè âòîðè÷íàÿ ìàòðèöà îáëàäàåò îäíèì èç òðåõ ïåðâûõ ïðèçíàêîâ, òî
ñòðóêòóðíàÿ ñõåìà ïîëíîñòüþ îïðåäåëåíà.  íàøåì ñëó÷àå âòîðè÷íàÿ ìàò-
ðèöà îáëàäàåò ïðèçíàêîì 2. Ïîýòîìó ìîæíî çàïèñàòü:
( )
PT p p
i
i
n
i
in
N
( )
g
= - -
é
ë
ê
ê
ù
û
ú
ú
= =+
Õ Õ
1 1
1 1 . (6.77)
Ïðèçíàê 6. Åñëè ïåðâè÷íàÿ ìàòðèöà îáëàäàåò íåêîòîðûìè ñâîéñòâàìè
ïðèçíàêà 5, íî ñðåäè ÷ëåíîâ ðÿäà x
i
è ðÿäà y
i
åñòü òàêèå, êîòîðûå óäîâëå-
òâîðÿþò óñëîâèÿì (ñì.ðèñ.6.17)
x
1
= x
2
= ... = x
n
= N, x
n+1
= x
n+2
= ... = x
s
= s,
y
1
= y
2
= ... = y
n
= n; y
n+1
= y
n+2
= ... = y
s
= N, (6.78)
{a
n+1
Úa
n+2
Ú..Úa
s
} º s; n + s = N,
òî ýëåìåíòû ñ íîìåðàìè a
1
, a
2
, ..., a
n
, ñîåäèíåíû ìåæäó ñîáîé ïîñëåäîâà-
òåëüíî è ó íèõ ïîä îáùåé ñòðåëêîé ðàñïîëîæåíû ñîåäèíåííûå ìåæäó ñî-
áîé ïîñëåäîâàòåëüíî ýëåìåíòû ñ íîìåðàìè a
n+1
, a
n+2
, ..., a
N
.
 íàøåì ïðèìåðå
PT p
i
i
n
( )
g
=
=
Õ
1
. (6.79)
Ïðè ýòîì õàðàêòåðèñòèêè âòîðè÷íîé ìàòðèöû (äëÿ ýëåìåíòîâ ïîä
ñòðåëêîé) áóäóò îïðåäåëÿòüñÿ ïî çàâèñèìîñòÿì:
N
2
=N-n, x
i
(2)
=x
i
, y
i
(2)
=y
i
-n, M
2
=M-(s+n)N+sn, i=n+1,n+2,...,N. (6.80)
Ìîæíî óáåäèòñÿ, ÷òî âòîðè÷íàÿ ìàòðèöà äëÿ ýëåìåíòîâ ïîä ñòðåëêîé â
íàøåì ïðèìåðå îáëàäàåò ïðèçíàêîì 1.
Õàðàêòåðèñòèêè âòîðè÷íîé ìàòðèöû äëÿ áàçîâûõ ýëåìåíòîâ îïðåäåëÿ-
þòñÿ çàâèñèìîñòÿìè
N
2
= N-s, x
i
(2)
= x
i
-s, y
i
(2)
= y
i
, M
2
= M-(s+n)N+sn, i = 1,2,...,n. (6.81)
Òàê êàê ïî ïðèçíàêó 6 l+s=N, òî âòîðè÷íàÿ ìàòðèöà òàêæå îáëàäàåò
ïðèçíàêîì 1.
Ìîãóò áûòü ïîëó÷åíû ïðèçíàêè ïåðâè÷íûõ ìàòðèö ëþáîé ñëîæíîñòè,
èç êîòîðûõ ïóòåì ïîñëåäîâàòåëüíîãî ïîñòðîåíèÿ ìàòðèö áîëåå âûñîêîãî
ïîðÿäêà ìîãóò áûòü âûäåëåíû ìàòðèöû ñ ïåðâûìè òðåìÿ ïðèçíàêàìè.
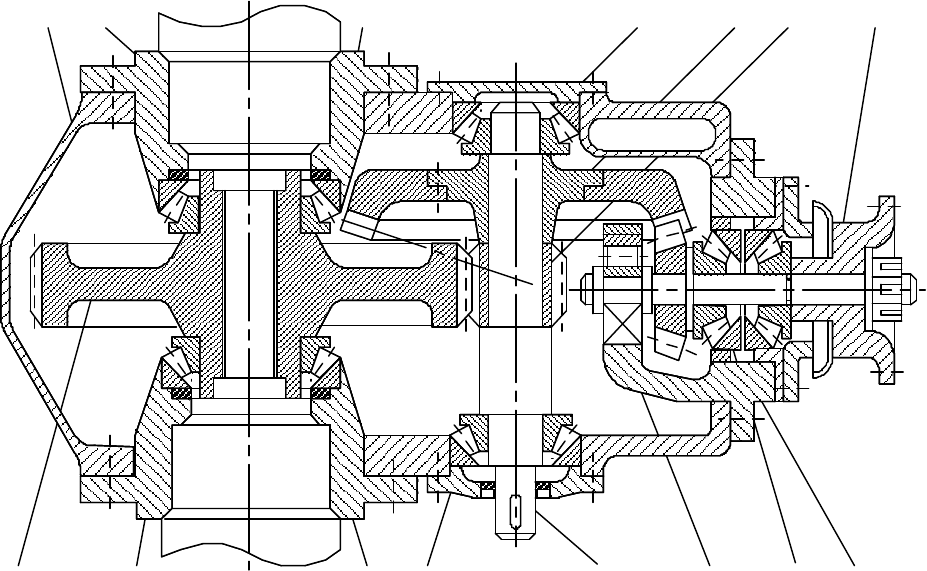
Ïðèìåð 6.23 [11]. Ðàññìîòðèì ïîñëåäîâàòåëüíîñòü ñòðóêòóðíîãî àíàëèçà íà ïðèìå-
ðå ðåäóêòîðà çàäíåãî ìîñòà àâòîãðåéäåðà (ðèñ 6.4). Òîãäà èñõîäíàÿ èíôîðìàöèÿ î ðå-
ìîíòîïðèãîäíîñòè çàäíåãî ìîñòà ìîæåò áûòü ïðåäñòàâëåíà ÷åðåç õàðàêòåðèñòèêó äîñ-
òóïíîñòè êàæäîé äåòàëè, êîòîðóþ ìîæíî çàïèñàòü â ñëåäóþùåì âèäå:
1 (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15) 9 (8)
2 (3, 4, 5, 6) 10 (11)
3 (4, 5, 6) 11 (10)
4 (3, 5, 6) 12 (13, 14, 15)
5 (3, 4, 6) 13
6 14
7 (8, 9, 10, 11) 15
8 (9)
N=15; M=53.
52
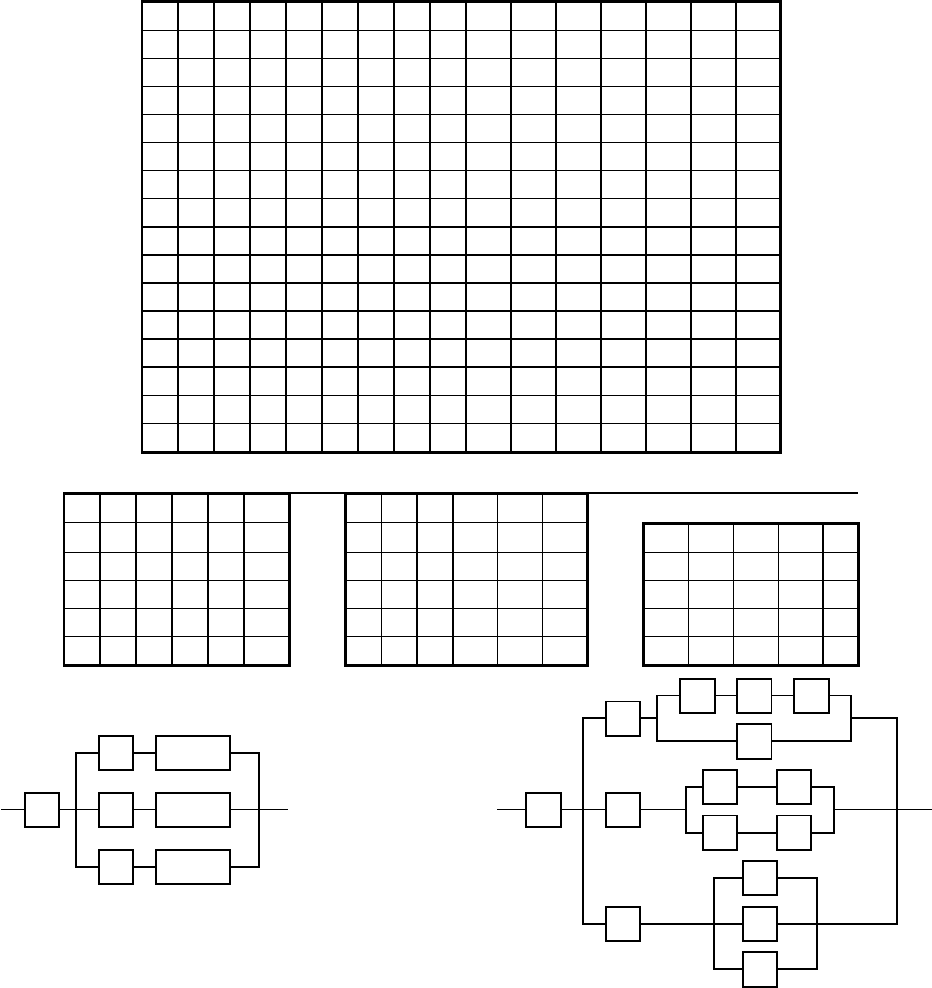
Ïî èñõîäíîé èíôîðìàöèè ñîñòàâèì ïåðâè÷íóþ ìàòðèöó (ðèñ.6.19), ñ ïîìîùüþ êîòî-
ðîé îïðåäåëèì ïðèçíàêè, óêàçûâàþùèå íà ïîëîæåíèå êàæäîãî ýëåìåíòà â ñòðóêòóðíîé
ñõåìå íàäåæíîñòè ìîñòà.
Ïîñêîëüêó ïî âûðàæåíèÿì (6.72) 15<M<(15+15
2
)/2, òî ïåðâè÷íàÿ ìàòðèöà îáëàäàåò
ïðèçíàêîì 4, ó êîòîðîé òîëüêî äëÿ ýëåìåíòà 1 x
1
=15 è y
1
=1, ÷òî ñîîòâåòñòâóåò áàçî-
âîìó ýëåìåíòó ïî ïðèçíàêó 5.
Ïîñëå îòäåëåíèÿ áàçîâîãî ýëåìåíòà ñîãëàñíî (6.76) ïîëó÷èì âòîðè÷íóþ ìàòðèöó ñî
ñëåäóþùèìè âíåøíèìè õàðàêòåðèñòèêàìè:
N
2
= N - n = 14; M
2
= M - nN = 35; x
i
(2)
= x
i
; y
i
(2)
= y
i
- 1.
Ïîëó÷åííàÿ ìàòðèöà ðàçäåëÿåòñÿ íà òðè íåïåðåñåêàþùèåñÿ ìàòðèöû òðåòüåãî ïîðÿä-
êà, ýëåìåíòû êîòîðûõ îáðàçóþò òðè ïàðàëëåëüíûõ âåòâè ñòðóêòóðíîé ñõåìû.
Âñå âíîâü îáðàçîâàííûå ìàòðèöû îáëàäàþò ïðèçíàêàìè 4 è 5, ïîñêîëüêó äëÿ êàæäîé
âåòâè èìååòñÿ ïî îäíîìó áàçîâîìó ýëåìåíòó (ñîîòâåòñòâåííî, 2, 7 è 12), êîòîðûå îòäå-
ëÿþòñÿ äëÿ îáðàçîâàíèÿ ìàòðèö ÷åòâåðòîãî ïîðÿäêà è óñòàíîâëåíèÿ ñâÿçè ìåæäó ýëå-
ìåíòàìè âíóòðè êàæäîé ïàðàëëåëüíîé âåòâè ñòðóêòóðíîé ñõåìû.
Ìàòðèöû ÷åòâåðòîãî ïîðÿäêà (3-6) è (8-11) îáëàäàþò ïðèçíàêîì 4, à ìàòðèöà (13-15)
- ïðèçíàêîì 2. Ïîýòîìó äàëüíåéøèé àíàëèç ïðîâîäèòñÿ ñ ìàòðèöàìè (3-6) è (8-11).
Ìàòðèöà (3-6) äåëèòñÿ íà äâå ìàòðèöû ïÿòîãî ïîðÿäêà (3-5) è (6), ýëåìåíòû êîòîðûõ
ïàðàëëåëüíû ìåæäó ñîáîé.
Ìàòðèöà (3-5) îáëàäàåò îñíîâíûì ïðèçíàêîì 1, ïîýòîìó âñå åå ýëåìåíòû ñîåäèíåíû
ïîñëåäîâàòåëüíî.
Îñòàâøàÿñÿ ìàòðèöà (8-11) òàêæå äåëèòñÿ íà äâå ìàòðèöû ñ ïðèçíàêîì 1, ó êîòî-
ðûõ ýëåìåíòû 8 è 9 ñîåäèíåíû ïîñëåäîâàòåëüíî è îáðàçóþò ïàðàëëåëüíóþ âåòâü ñ ýëå-
ìåíòàìè 10 è 11, ñîåäèíåííûìè ìåæäó ñîáîé òàêæå ïîñëåäîâàòåëüíî.
Òàêèì îáðàçîì, âñå ýëåìåíòû çàíÿëè ñâîè ìåñòà â ñòðóêòóðíîé ñõåìå íàäåæíîñòè
ðåäóêòîðà çàäíåãî ìîñòà àâòîãðåéäåðà ïî êðèòåðèþ åãî ïðåäåëüíîãî ñîñòîÿíèÿ.
1
2
3
45
67
89
10 11
12
13
14 15
Ðèñ. 6.18. Ðåäóêòîð çàäíåãî ìîñòà àâòîãðåéäåðà:
1 - êîðïóñ; 2 - âàë; 3 - öèëèíäðè÷åñêàÿ øåñòåðíÿ; 4 - êîíè÷åñêîå êîëåñî; 5 - ïîäøèï-
íèê (ïðàâûé); 6 - ïîäøèïíèê ëåâûé; 7 - öèëèíäðè÷åñêîå êîëåñî; 8 - ïîäøèïíèê (ïðà-
âûé); 9 - ãîðëîâèíà (ïðàâàÿ); 10 - ïîäøèïíèê (ëåâûé); 11 - ãîðëîâèíà (ëåâàÿ); 12 -
âàë-øåñòåðíÿ; 13 - ñòàêàí; 14 - ïîäøèïíèê; 15 - ïîäøèïíèê ñäâîåííûé
(íîìåðàìè îáîçíà÷åíû òîëüêî äåòàëè, ÷åðåç êîòîðûå ïðîõîäèò ñèëîâîé ïîòîê)
53
Ïåðâè÷íàÿ ìàòðèöà
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
5
3
4
5
3
3
4
5
3
3
4
5
3
6
1
7
8
9
10
11
5
8
9
2
8
9
2
10
11
2
10
11
2
12
13
14
15
4
13
1
14
1
15
1
1
2
5
5
5
3
2
4
4
4
4
2
3
3
5
50
Ìàòðèöû òðåòüåãî ïîðÿäêà
2
3
4
5
6
5
7
8
9
10
11
5
3
4
5
3
8
9
2
12
13
14
15
4
3
4
5
3
8
9
2
13
1
3
4
5
3
10
11
2
14
1
1
10
11
2
15
1
1
4
4
4
2
15
1
3
3
3
3
13
1
2
2
2
7
3 4 5
6
8 9
10 11
13
14
15
2
7
12
11
2
7
12
3-6
8-11
13-15
Ðèñ.6.19. Ìàòðèöû ïîëîæåíèé ýëåìåíòîâ ðåäóêòîðà çàäíåãî ìîñòà àâòîãðåéäåðà
è ñîîòâåòñòâóþùèå èì ñòðóêòóðíûå ñõåìû
Ôîðìàëèçîâàííûé ìåòîä àíàëèçà ïîçâîëÿåò âûïîëíÿòü ïîñòðîåíèå
ñòðóêòóðíûõ ñõåì ïî êðèòåðèþ îòêàçà. Äëÿ ðåøåíèÿ ýòîé çàäà÷è íåîáõî-
äèìî âû÷èñëèòü îïåðàòèâíûå ðåìîíòíûå çàòðàòû ïðè çàìåíå êàæäîé äåòà-
ëè ñáîðî÷íîé åäèíèöû. Äëÿ ýòîãî ìîæíî âîñïîëüçîâàòüñÿ ïåðâè÷íîé ìàò-
ðèöåé, ñ ïîìîùüþ êîòîðîé îïðåäåëèòü äîëþ çàòðàò ïðè çàìåíå ëþáîé äå-
òàëè îò îáùåãî îáúåìà ðåìîíòíûõ çàòðàò ïðè êàïèòàëüíîì ðåìîíòå óçëà
âî âñåõ âîçìîæíûõ åãî âàðèàíòàõ.
Äëÿ îöåíêè ðåìîíòîïðèãîäíîñòè èçäåëèé íà ñòàäèè ïðîåêòèðîâàíèÿ ðå-
êîìåíäóåòñÿ ó÷èòûâàòü äîñòóïíîñòü è ëåãêîñúåìíîñòü êàæäîãî ýëåìåíòà
[25]. Äëÿ ýòîãî íåîáõîäèìî èñïîëüçîâàòü òîëüêî äîñòîâåðíóþ èíôîðìàöèþ.
Îñíîâíûìè ôàêòîðàìè, îïðåäåëÿþùèìè ëåãêîñúåìíîñòü, ÿâëÿþòñÿ ìàññà
ñíèìàåìûõ äåòàëåé, ÷èñëî êðåïåæíûõ ýëåìåíòîâ, ÷èñëî ìåñò ñòîðîííèÿ è

54
÷èñëî ñîåäèíåíèé ñ ïîñàäêîé. Ïðè íåîáõîäèìîñòè ÷èñëî ôàêòîðîâ, ñ ïî-
ìîùüþ êîòîðûõ ó÷èòûâàëîñü áû ïîëîæåíèå îïåðàòîðà, ñòåñíåííîñòü ìåñòà
ñúåìà, êîëè÷åñòâî ñëåñàðíîãî èíñòðóìåíòà, ìîæåò áûòü óâåëè÷åíî. Ñòå-
ïåíü âëèÿíèÿ êàæäîãî ôàêòîðà è âñåõ âìåñòè íà ïîêàçàòåëü ëåãêîñúåìíî-
ñòè ìîæåò áûòü óòî÷íåíà ïîñëå èçãîòîâëåíèÿ îïûòíîãî îáðàçöà è ïðîâå-
äåíèÿ èñïûòàíèé íà ðåìîíòîïðèãîäíîñòü.
Íà ñòàäèè ïðîåêòèðîâàíèÿ èçâåñòíî êîìïîíîâî÷íîå ðåøåíèå êîíñòðóê-
öèè ñáîðî÷íîé åäèíèöû, êîòîðîå äàåò âîçìîæíîñòü îïðåäåëèòü ÷èñëî ïðåä-
âàðèòåëüíî ñíèìàåìûõ ýëåìåíòîâ ïðè çàìåíå îòêàçàâøåé äåòàëè. Îäíî-
âðåìåííî ñ ýòîé èíôîðìàöèåé ìîæíî óñòàíîâèòü îáùóþ ìàññó ñíèìàåìûõ
ýëåìåíòîâ (ïðåäâàðèòåëüíî ñíÿòûõ è îòêàçàâøåãî ýëåìåíòà) åg
i
îáùåå
÷èñëî êðåïåæíûõ ýëåìåíòîâ ån
êi
, îáùåå ÷èñëî ñòîïîðíûõ ýëåìåíòîâ
ån
ñòi
, è îáùåå ÷èñëî ñîåäèíåíèé ñ ïîñàäêîé ån
ïñi
, êîòîðûå íåîáõîäèìî
ñíÿòü è ðàçúåäèíèòü äëÿ òîãî, ÷òîáû çàìåíèòü îòêàçàâøèé ýëåìåíò. Èç
÷åðòåæà èçâåñòíû ìàññà ñáîðî÷íîé åäèíèöû G
i
, îáùåå ÷èñëî êðåïåæíûõ
N
êi
è ñòîïîðíûõ N
ñòi
ýëåìåíòîâ, îáùåå ÷èñëî ïîñàäî÷íûõ ñîåäèíåíèé
N
ïñi
. Òîãäà ìîæíî ïîëó÷àòü ïîêàçàòåëè ëåãêîñúåìíîñòè äåòàëè ïî êàæäîìó
ôàêòîðó â îòäåëüíîñòè:
- ïî ìàññå ñíèìàåìûõ äåòàëåé: a
i
(1)
= åg
i
/G
i
;
- ïî ÷èñëó ìåñò êðåïëåíèÿ: a
i
(2)
= ån
êi
/N
êi
;
- ïî ÷èñëó ìåñò ñòîïîðåíèÿ: a
i
(3)
= ån
ñòi
/N
ñòi
;
- ïî ÷èñëó ñîåäèíåíèé ñ ïîñàäêîé: a
i
(4)
= ån
ïñi
/N
ïñi
.
Ïðèíèìàÿ â ïåðâîì ïðèáëèæåíèè íåçàâèñèìîñòü è ðàâíîçíà÷íîñòü êà-
æäîãî èç ôàêòîðîâ, ïîëó÷èì ñðåäíåâçâåøåííóþ îöåíêó ëåãêîäîñòóïíîñòè ñ
ó÷åòîì ïîêàçàòåëåé ëåãêîñúåìíîñòè
x
i
(
a
)
= (a
i
(1)
+ a
i
(2)
+ a
i
(3)
+ a
i
(4)
)/n
a
(6.82)
ãäå n
a
- ÷èñëî ó÷èòûâàåìûõ ïîêàçàòåëåé ëåãêîñúåìíîñòè.
Èç ïåðâè÷íîé ìàòðèöû ñëåäóåò, ÷òî íåîáõîäèìîñòü ñíÿòèÿ êàæäîé äå-
òàëè îïðåäåëÿåòñÿ íå òîëüêî åå îòêàçîì, íî è îòêàçàìè äðóãèõ äåòàëåé,
äëÿ çàìåíû êîòîðûõ äàííàÿ äåòàëü äîëæíà áûòü ñíÿòà. Ïîýòîìó ïîëíàÿ
õàðàêòåðèñòèêà ðåìîíòîïðèãîäíîñòè äîëæíà ó÷èòûâàòü ÷àñòîòó òàêèõ ñè-
òóàöèé â îáùåì ìàññèâå âñåõ âîçìîæíûõ ñëó÷àåâ ñíÿòèÿ äåòàëåé ñáîðî÷-
íîé åäèíèöû. Ýòà ÷àñòîòà îïðåäåëÿåòñÿ îòíîøåíèåì âíåøíèõ õàðàêòåðè-
ñòèê ïåðâè÷íîé ìàòðèöû (y
i
-1)/M.
Òåïåðü ìîæíî îïðåäåëèòü ñðåäíèå îïåðàòèâíûå ðåìîíòíûå çàòðàòû
(èëè èõ ðàíãè) ïðè íåîáõîäèìîñòè çàìåíû ëþáîé îòêàçàâøåé äåòàëè:
() ()
z z z x
y
M
i
ïçj
i
ñj
i
i
= + +
-
æ
è
ç
ö
ø
÷
ð
a
1
1
, (6.83)
() ()
R R R x
y
M
i
ïçj
i
ñj
i
i
= + +
-
æ
è
ç
ö
ø
÷
ð
a
1
1
(6.84)
ãäå z
(i)
ïçj
, R
(i)
ïçj
- ñðåäíèå ðåìîíòíûå çàòðàòû (ðàíã), îïðåäåëÿåìûå ïîäãîòîâèòåëüíî-
çàêëþ÷èòåëüíûìè îïåðàöèÿìè, âûïîëíÿåìûå íà ìàøèíå è ïðåäíàçíà÷åííûå äëÿ îáåñ-
ïå÷åíèÿ íåîáõîäèìîãî äîñòóïà ê ñáîðî÷íîé åäèíèöå â ñâÿçè ñ çàìåíîé i-é äåòàëè; z
pcj
;
R
pcj
- ñðåäíèå ðåìîíòíûå çàòðàòû (ðàíãè), îïðåäåëÿåìûå îïåðàöèÿìè ïîëíîé ðàçáîðêè
è ïîñëåäóþùåé ñáîðêè óçëà ïðè åãî êàïèòàëüíîì ðåìîíòå: R
pcj
= R
j
- R
(i)
ïçj
.
55
Åñëè çàäàí êðèòåðèé îòêàçà ÷åðåç ìèíèìàëüíûå îïåðàòèâíûå çàòðàòû
ïî âîññòàíîâëåíèþ ðàáîòîñïîñîáíîñòè z
0
(èëè åãî ðàíã R
0
), òî, èñïîëüçóÿ
ðÿä çíà÷åíèé îïåðàòèâíûõ ðåìîíòíûõ çàòðàò äëÿ êàæäîé äåòàëè ïî ôîð-
ìóëå (6.83) èëè èõ ðàíãîâ ïî ôîðìóëå (6.84), ìîæíî ïîëó÷èòü íîâûé ðÿä
ðàíãîâ îòíîñèòåëüíî íîâîãî êðèòåðèÿ ïî îòíîøåíèþ
R
i
0
= z
i
/z
0
= R
i
/R
0
. (6.85)
Ýòîò ðÿä ðàíãîâ ïîçâîëÿåò ïîëó÷èòü ñòðóêòóðíóþ ôîðìóëó è ñòðóêòóð-
íóþ ñõåìó áåçîòêàçíîñòè ñáîðî÷íîé åäèíèöû ïî âûáðàííîìó êðèòåðèþ.
6.4.3. Прогнозирование распределения наработки до первого
отказа
Ïðèíöèï ïðîãíîçèðîâàíèÿ êðèâûõ ðàñïðåäåëåíèÿ ðåñóðñà ìàøèíû ïî
ýêîíîìè÷åñêîìó êðèòåðèþ ïðåäåëüíîãî ñîñòîÿíèÿ ìîæåò áûòü èñïîëüçîâàí
äëÿ ïðîãíîçèðîâàíèÿ êðèâûõ ðàñïðåäåëåíèÿ íàðàáîòêè äî ïåðâîãî îòêàçà,
êðèòåðèé êîòîðîãî îïðåäåëåí ìèíèìàëüíûìè îïåðàòèâíûìè çàòðàòàìè íà
âîññòàíîâëåíèå ðàáîòîñïîñîáíîñòè èëè ñîîòâåòñòâóþùèì åìó ðàíãîì ðå-
ìîíòíûõ çàòðàò.
Ñóùåñòâóåò òðè ãðóïïû ñëîæíîñòè îòêàçîâ, ðàçëè÷àþùèåñÿ îáúåìîì
ðåìîíòíûõ ðàáîò. Îäíàêî òàêàÿ ãðàäàöèÿ îòêàçîâ ÿâëÿåòñÿ óñëîâíîé, ïî-
ñêîëüêó ñ ñîâåðøåíñòâîâàíèåì êîíñòðóêöèé ìàøèí è ñ èçìåíåíèåì òðåáî-
âàíèé ïîòðåáèòåëÿ äîïóñòèìûå ïðåäåëû ýêîíîìè÷åñêèõ ïîñëåäñòâèé îòêà-
çîâ áóäóò ñíèæàòüñÿ.
Åäèíàÿ êëàññèôèêàöèÿ îòêàçîâ ïî ãðóïïàì ñëîæíîñòè äëÿ èçäåëèé âñåõ
îòðàñëåé ìàøèíîñòðîåíèÿ íåâîçìîæíà. Íàïðèìåð, îòêàçû òðåòüåé ãðóïïû
ñëîæíîñòè, ïðèíÿòûå â òðàêòîðíîé ïðîìûøëåííîñòè, õàðàêòåðèçóþòñÿ
òåì, ÷òî äëÿ èõ óñòðàíåíèÿ òðåáóåòñÿ ðàçáîðêà èëè ðàñ÷ëåíåíèå îñíîâíûõ
àãðåãàòîâ (òðàíñìèññèè, õîäîâîé ÷àñòè). Òàêèå ïîñëåäñòâèÿ â ñòðîèòåëü-
íîì è äîðîæíîì ìàøèíîñòðîåíèè êëàññèôèöèðóþòñÿ êàê êðèòåðèè ïðå-
äåëüíîãî ñîñòîÿíèÿ, ïî êîòîðîìó ôèêñèðóåòñÿ ðåñóðñ ìàøèíû äî êàïè-
òàëüíîãî ðåìîíòà. Ïîýòîìó åäèíñòâåííî âåðíûì ÿâëÿåòñÿ èíäèâèäóàëüíûé
ïîäõîä ê îïðåäåëåíèþ ïîíÿòèÿ îòêàçà äëÿ êàæäîé êîíêðåòíîé ìàøèíû â
çàâèñèìîñòè îò åå íàçíà÷åíèÿ, óñëîâèé èçãîòîâëåíèÿ è ýêñïëóàòàöèè.
Åñëè óñòàíîâëåíà âåðõíÿÿ ãðàíèöà äîïóñòèìûõ ïðåäåëüíûõ çàòðàò z
0
(èëè ñîîòâåòñòâóþùèé ðàíã îòêàçà R
0
), òî ìîæíî îïðåäåëèòü ðÿä ðàíãîâ
ðåìîíòíûõ çàòðàò ïî îòíîøåíèþ ê çàäàííîìó êðèòåðèþ îòêàçà. Ýòî äàñò
âîçìîæíîñòü ïîñòðîèòü ñòðóêòóðíóþ ñõåìó íàäåæíîñòè ñáîðî÷íîé åäèíè-
öû (èëè ìàøèíû â öåëîì) ïî çàäàííîìó êðèòåðèþ, ïîñòðîèòü êðèâóþ ðàñ-
ïðåäåëåíèÿ íàðàáîòêè ñáîðî÷íîé åäèíèöû (èëè ìàøèíû) äî ïåðâîãî îòêàçà
è îïðåäåëèòü åå ïàðàìåòðû. Ìàòåìàòè÷åñêîå îæèäàíèå ýòîãî ðàñïðåäåëå-
íèÿ ÿâëÿåòñÿ ñðåäíåé íàðàáîòêîé èçäåëèÿ äî îòêàçà.
Ïðèìåð 6.24 [11]. Ðàññìîòðèì íà ïðèìåðå çàäíåãî ìîñòà àâòîãðåéäåðà âëèÿíèå
óðîâíÿ êðèòåðèÿ îòêàçà z
0
íà âåëè÷èíó ñðåäíåé íàðàáîòêè äî ïåðâîãî îòêàçà. Ðàñ÷åò
ðàíãîâ ðåìîíòíûõ çàòðàò äëÿ ðàçëè÷íûõ z
0
ñâåäåí â òàáë.6.18. Ïî äàííûì òàáë.6.18
ñòðóêòóðíûå ôîðìóëû ê ðàñ÷åòó ñðåäíåé íàðàáîòêè äî ïåðâîãî îòêàçà äëÿ ðàçëè÷íûõ
âàðèàíòîâ áóäóò èìåòü âèä (äëÿ âñåõ âàðèàíòîâ a
0
=0.7):
- äëÿ âàðèàíòà I
( )
()
Ptz pt
I
i
i
,
0
1
15
=
=
Õ
;
56
- äëÿ âàðèàíòà II
( )
() ()
[ ]
()
[ ]
{ }
Ptz pt pt pt
II
i
i
,
0
1
13
14 15
1 1 1=
é
ë
ê
ù
û
ú
- - -
=
Õ
;
- äëÿ âàðèàíòîâ III è IV
( )
() ()
[ ]
()
[ ]
{ }
()
[ ]
()
[ ]
{ }
Ptz pt pt pt pt pt
IIIIV
i
i
,
,
0
1
11
12 15 13 14
1 1 1 1 1 1=
é
ë
ê
ù
û
ú
- - - - - -
=
Õ
;
- äëÿ âàðèàíòà V
( )
() ()
[ ]
()
[ ]
{ }
()
[ ]
()
[ ]
{ }
()
[ ]
()
[ ]
{ }
()
[ ]
()
[ ]
{ }
Ptz pt pt pt pt p t
p t pt pt pt
V
i
i
,
.
0
1
7
8 15 9 14
10 13 11 12
1 1 1 1 1 1
1 1 1 1 1 1
=
é
ë
ê
ù
û
ú
- - - - - - ´
´ - - - - - -
=
Õ
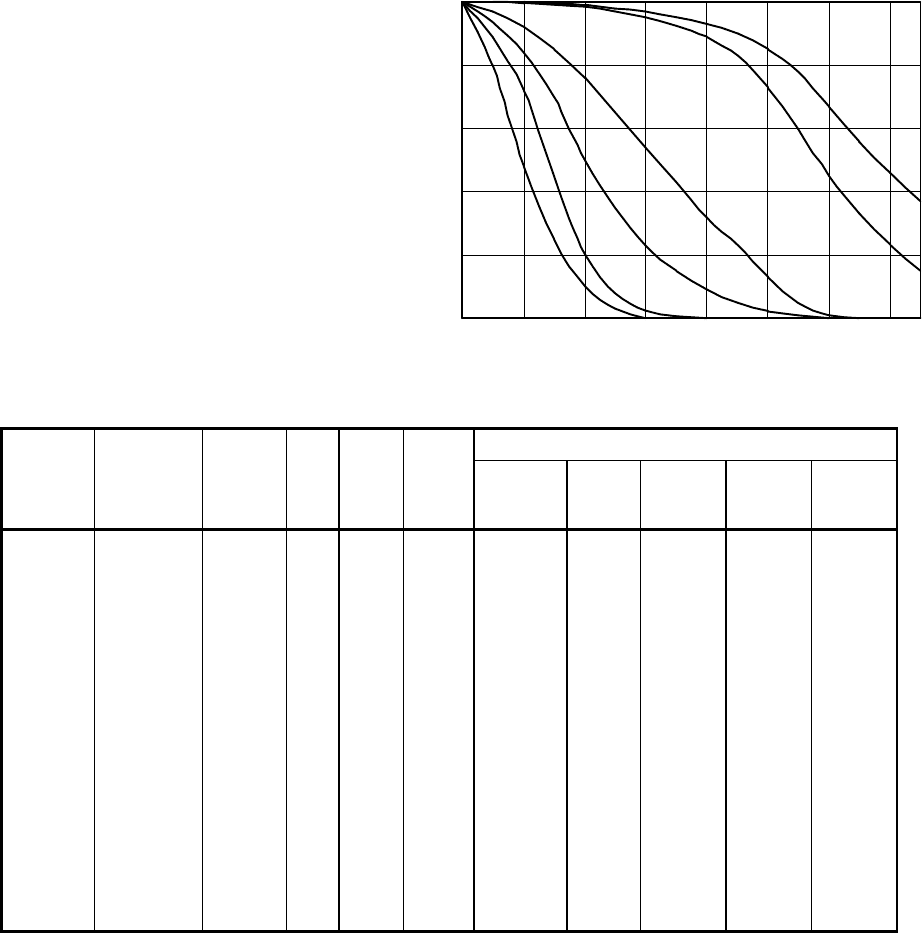
Êðèâûå ðàñïðåäåëåíèÿ ñðåäíåé íàðàáîòêè ðåäóêòîðà çàäíåãî ìîñòà äî ïåðâîãî îòêàçà
ïðåäñòàâëåíû íà ðèñ.6.20. Ýòè êðèâûå ðàñïðåäåëåíèÿ ïîçâîëÿþò îïðåäåëèòü âåðîÿò-
íîñòü áåçîòêàçíîé ðàáîòû ìîñòà äëÿ ëþáîé åãî íàðàáîòêè ñ çàäàííûì âàðèàíòîì êðè-
òåðèÿ îòêàçà. Ïðè ýòîì çàêîíû ðàñïðåäåëåíèÿ ðåñóðñîâ äåòàëåé óçëà ìîãóò áûòü ðàç-
ëè÷íûìè. Îäíîâðåìåííî ñ ïðîãíîçîì êðèâîé ðàñïðåäåëåíèÿ ìîæåò áûòü âûïîëíåí ðàñ-
÷åò çàòðàò íà âîññòàíîâëåíèå îòêàçà íà ëþáîé ìîìåíò âðåìåíè ïðè óñëîâèè, ÷òî äî
ýòîãî ìîìåíòà îòêàçà íå áûëî. Íàðàáîòêà íà îòêàç ñáîðî÷íîé åäèíèöû îïðåäåëÿåòñÿ
ïóòåì íàõîæäåíèÿ êîìïîçèöèé ðàñïðåäåëåíèé ðåñóðñîâ çàìåíÿåìûõ äåòàëåé è ñóïåðïî-
çèöèåé ñìåñè ðàñïðåäåëåíèé.
Ðèñ.6.20. Êðèâûå ðàñïðåäåëåíèÿ
ñðåäíåé íàðàáîòêè ðåäóêòîðà
äî ïåðâîãî îòêàçà:
1 - z
0
I
³ 3,6 ÷; 2 - z
0
II
³ 8 ÷;
3 - z
0
III
³ 10 ÷ è z
0
IV
³ 12 ÷;
4 - z
0
V
³ 16 ÷;
5 - z
i
³ 36 ÷ (êðèâàÿ óáûëè ðåñóðñà
ïî ðàíãîâîé ñòðóêòóðíîé ñõåìå);
6 - z
i
³ 36 ÷ (êðèâàÿ óáûëè ðåñóðñà
ïî ïåðâè÷íîé ñòðóêòóðíîé ñõåìå
ðèñ.6.19).
Òàáëèöà 6.18
РАСЧЕТ РАНГОВ РЕМОНТНЫХ ЗАТРАТ
Âèä
Ðàíãè ðåìîíòíûõ çàòðàò R
j
0
Íîìåð
äåòàëè
ðàñïðå-
äåëåíèÿ
T
i
, ÷.
v
i
R
i
z
i
, ÷.
z
0
I
³3,6 ÷.
z
0
II
³8 ÷.
z
0
III
³10 ÷.
z
0
IV
³12 ÷.
z
0
V
³16 ÷.
1 Â 30000
0,5
0,47
36
10,0
4,50
3,60
3,00
2,25
2 Â 25000
0,4
0,28
21,2
5,9 2,65
2,12
1,77
1,33
3 Í 12000
0,2
0,26
20,2
5,6 2,53
2,02
1,68
1,26
4 Í 12000
0,2
0,28
21,6
6,0 2,70
2,16
1,80
1,35
5 Â 18000
0,7
0,27
20,5
5,7 2,56
2,05
1,71
1,28
6 Â 18000
0,7
0,24
18,4
5,1 2,30
1,84
1,53
1,15
7 Í 12000
0,2
0,26
19,8
5,5 2,50
1,98
1,65
1,24
8 Â 20000
0,7
0,16
12,2
3,4 1,53
1,22
1,00
0,76
9 Â 20000
0,5
0,16
12,2
3,4 1,53
1,22
1,00
0,76
10 Â 20000
0,7
0,16
12,2
3,4 1,53
1,22
1,00
0,76
11 Â 20000
0,5
0,16
12,2
3,4 1,53
1,22
1,00
0,76
12 Â 3500
0,4
0,10
7,9
2,2 0,99
0,79
0,66
0,49
13 Â 20000
0,5
0,9
6,8
1,9 0,85
0,68
0,57
0,43
14 Â 5400
0,7
0,5
4,0
1,1 0,50
0,40
0,33
0,25
15 Â 7400
0,7
0,5
3,6
1,0 0,45
0,36
0,30
0,23
0
0,2
0,4
0,6
0,8
P(t)
0
2
4
6
8
10
T
×10
-
3
,
÷
1
2
3
4
5
6

57
6.4.4. Требования к ресурсам деталей и ремонтопригодности узлов
Òðåáîâàíèÿ ê ðåñóðñíûì ïîêàçàòåëÿì äåòàëåé ðàçðàáàòûâàþòñÿ ñ ó÷å-
òîì ðàñïîëîæåíèÿ êàæäîé äåòàëè â ñòðóêòóðíîé ñõåìå óçëà è ñàìîãî óçëà
â ñòðóêòóðíîé ñõåìå ìàøèíû, òàêèì îáðàçîì ó÷èòûâàþòñÿ âëèÿíèå ïî-
ñëåäñòâèé îòêàçà äåòàëåé íà óðîâåíü ðåìîíòîïðèãîäíîñòè ìàøèíû.
Âî âñåõ ñëó÷àÿõ, êîãäà äåòàëü â ñòðóêòóðíîé ñõåìå óçëà ðàñïîëîæåíà
ïîñëåäîâàòåëüíî, åå íàðàáîòêà äî çàìåíû äîëæíà áûòü íå ìåíåå íàðàáîòêè
ñàìîãî óçëà, ò.å.
T
j
= T
i
ïðè R
i
= R
j
, (6.86)
ãäå T
j
- íàðàáîòêà ìàøèíû äî çàìåíû j-é äåòàëè; R
j
- ðàíã ðåìîíòíûõ çàòðàò íà çàìåíó
äåòàëè ñ ó÷åòîì äîñòóïíîñòè è ëåãêîñúåìíîñòè.
Óñëîâèå (6.86) ñïðàâåäëèâî äëÿ ëþáîãî óçëà, êàê áû îí íè áûë ðàñïî-
ëîæåí â ñòðóêòóðíîé ñõåìå ìàøèíû.
Îñîáîå ìåñòî â àíàëèçå ðåìîíòíûõ çàòðàò çàíèìàþò óçëû, ïîñëåäîâà-
òåëüíî ðàñïîëîæåííûå â ñòðóêòóðíîé ñõåìå ìàøèíû. Äëÿ òàêèõ óçëîâ
äîëæíû áûòü ïðîàíàëèçèðîâàíû ïîñëåäñòâèÿ îòêàçîâ äàæå òàêèõ ýëåìåí-
òîâ, êîòîðûå â ñòðóêòóðíîé ñõåìå óçëà ðàñïîëîæåíû â ïàðàëëåëüíûõ âåò-
âÿõ. Ïîýòîìó íåîáõîäèìî ðàññìîòðåòü âñå ñîñòàâíûå ÷àñòè ýòèõ çàòðàò è
îöåíèòü èõ âëèÿíèå íà ïîñëåäñòâèÿ îòêàçîâ äåòàëåé, ðàñïîëîæåííûõ â ïà-
ðàëëåëüíûõ âåòâÿõ ñòðóêòóðíîé ñõåìû óçëà.
 òîì ñëó÷àå, êîãäà çàòðàòû íà ïîäãîòîâèòåëüíî-çàêëþ÷èòåëüíûå îïå-
ðàöèè ïî çàìåíå óçëà ïðåâûøàþò íîðìàòèâ òåêóùåãî ðåìîíòà èëè ðàâíû
åìó, íè îäíà äåòàëü íå äîëæíà èìåòü ðåñóðñ ìåíåå ðåñóðñà ñàìîãî óçëà äî
åãî çàìåíû (èëè êàïèòàëüíîãî ðåìîíòà).
Åñëè çàòðàòû íà ïîäãîòîâèòåëüíî-çàêëþ÷èòåëüíûå îïåðàöèè ïî çàìåíå
óçëà ìåíüøå íîðìàòèâà òåêóùåãî ðåìîíòà, òî äåòàëè, ðàñïîëîæåííûå ïà-
ðàëëåëüíî â ñòðóêòóðíîé ñõåìå óçäà, ìîãóò áûòü çàìåíåíû ïðè ëþáîì òå-
êóùåì ðåìîíòå.
Óñëîâèå äëÿ çàìåíû ëåãêîäîñòóïíûõ äåòàëåé îñíîâíûõ óçëîâ ìîæíî
çàïèñàòü â ñëåäóþùåì âèäå:
(
)
()
T
T NT R
T
N
R
N
i
i iê
ïçi
j
ê
i
ïçi
j
i
=
= ³
<
ì
í
ï
î
ï
=
1
1
12
ïðè
ïðè
a
a
;
;
,,....
(6.87)
Ñðåäíèé ðåñóðñ äåòàëè äî çàìåíû
T
i
= T
i
K
i
K
j
, (6.88)
ãäå K
i
- êîýôôèöèåíò èñïîëüçîâàíèÿ äåòàëè â ðàáî÷åì âðåìåíè óçëà; K
i
- êîýôôèöèåíò
èñïîëüçîâàíèÿ óçëà â ðàáî÷èõ è âñïîìîãàòåëüíûõ îïåðàöèÿõ ìàøèíû.
Ïî ñòàòèñòè÷åñêèì äàííûì î ðåñóðñàõ àíàëîãè÷íûõ äåòàëåé îïðåäåëÿ-
þòñÿ êîýôôèöèåíòû âàðèàöèè ïðåäïîëàãàåìîãî ðàñïðåäåëåíèÿ ðåñóðñà êà-
æäîé äåòàëè äî çàìåíû v
i
.
Ãàììà ïðîöåíòíûé ðåñóðñ äåòàëåé
t
g
i
= t
i
/K
g
i
= t
i
(1 - u
g
i
v
i
), (6.89)
ãäå K
g
i
= 1/(1-u
g
i
v
i
) - îòíîøåíèå ñðåäíåãî è ãàììà-ïðîöåíòíîãî ðåñóðñîâ äåòàëè ïî çà-
äàííûì çíà÷åíèÿì âåðîÿòíîñòè g
j
è v
j
.

58
Ïî ïîëó÷åííûì òðåáîâàíèÿì ê ðåñóðñíûì ïîêàçàòåëÿì äåòàëåé îïðåäå-
ëÿþòñÿ íîìåíêëàòóðà çàïàñíûõ ÷àñòåé â êàæäîì âèäå ðåìîíòîâ, ñïîñîáû
îáåñïå÷åíèÿ ýòèõ òðåáîâàíèé ðàñ÷åòíûìè è ýêñïåðèìåíòàëüíûìè ìåòîäà-
ìè, à òàêæå íåîáõîäèìîñòü ïðîåêòèðîâàíèÿ îáîðóäîâàíèÿ äëÿ ïðîâåäåíèÿ
ðåñóðñíûõ èñïûòàíèé íà ïîñëåäóþùèõ ñòàäèÿõ îòðàáîòêè ñáîðî÷íûõ åäè-
íèö.
Òðåáîâàíèÿ ê ïîêàçàòåëÿì ðåìîíòîïðèãîäíîñòè ñáîðî÷íûõ åäèíèö
(ñðåäíåé îïåðàòèâíîé òðóäîåìêîñòè, ïðîäîëæèòåëüíîñòè è ñòîèìîñòè êà-
ïèòàëüíîãî ðåìîíòà èëè çàìåíû) ôîðìóëèðóþòñÿ ïðè ïðîâåäåíèè ñòðóê-
òóðíîãî àíàëèçà íàäåæíîñòè ìàøèíû â öåëîì íà ýòàïå ðàçðàáîòêè òåõíè-
÷åñêîãî çàäàíèÿ íà åå ïðîåêòèðîâàíèå è îïðåäåëÿþòñÿ âûáðàííûì êðèòå-
ðèåì ïðåäåëüíîãî ñîñòîÿíèÿ ìàøèíû. Îäíàêî íà ñëåäóþùèõ ñòàäèÿõ ïðî-
åêòèðîâàíèÿ ýòè òðåáîâàíèÿ ìîãóò áûòü óòî÷íåíû ñ ó÷åòîì òðåáîâàíèé ê
êîìïëåêñíûì ïîêàçàòåëÿì íàäåæíîñòè (êîýôôèöèåíòàì ãîòîâíîñòè K
ã
è
òåõíè÷åñêîãî èñïîëüçîâàíèÿ Ê
òè
).
Îáû÷íî K
ã
= 0,9¸0,99 [11], ïîýòîìó ñðåäíÿÿ ñóììàðíàÿ ïðîäîëæèòåëü-
íîñòü âîññòàíîâëåíèÿ ìàøèíû ïîñëå îòêàçà
0,1×T ³ t
b
S
³ 0,01×T, (6.90)
ãäå Ò - ñðåäíèé ðåñóðñ ìàøèíû, ÷.
Ñðåäíÿÿ îïåðàòèâíàÿ ïðîäîëæèòåëüíîñòü ðåìîíòîâ è òåõíè÷åñêèõ îá-
ñëóæèâàíèé ïðè êîýôôèöèåíòå òåõíè÷åñêîãî èñïîëüçîâàíèÿ Ê
òè
=
0,8¸0,95
0,25×T ³ t
îá
³ 0,05×T. (6.91)
Ðàçíîñòü ìåæäó çíà÷åíèÿìè îïåðàòèâíûõ ïðîäîëæèòåëüíîñòåé ïî ôîð-
ìóëàì (6.90) è (6.91) - âåëè÷èíà ñðåäíåé îáúåäèíåííîé îïåðàòèâíîé ïðî-
äîëæèòåëüíîñòè ïëàíîâûõ ðåìîíòîâ è òåõíè÷åñêèõ îáñëóæèâàíèé:
0,15×T ³ t
îá
ïë
³ 0,04×T. (6.92)
Ïîñêîëüêó t
îá
ïë
= t
ð
S
+t
òî
S
, òî, çàäàâøèñü çíà÷åíèåì ñðåäíåé ñóììàðíîé
ïðîäîëæèòåëüíîñòè òåõíè÷åñêèõ îáñëóæèâàíèé t
òî
S
, ìîæíî ïîëó÷èòü çíà-
÷åíèå ñðåäíåé ñóììàðíîé ïðîäîëæèòåëüíîñòè ïëàíîâûõ ðåìîíòîâ â ðå-
ìîíòíîì öèêëå, êîòîðîå íå äîëæíî ïðåâûøàòü çíà÷åíèÿ
t
ð
S
£ (0,15 ¸ 0,04)×T - t
òî
S
. (6.93)
Òàêèì îáðàçîì, ñ ïîìîùüþ ñòðóêòóðíîãî àíàëèçà ìîæíî îáîñíîâàòü
âàæíåéøèå ïîêàçàòåëè ðåìîíòîïðèãîäíîñòè íà ýòàïå ïðîåêòèðîâàíèÿ.
Êîýôôèöèåíòû ëåãêîäîñòóïíîñòè è ïîìåõ äëÿ ñáîðî÷íîé åäèíèöû ìî-
ãóò áûòü ïîëó÷åíû èç âíåøíèõ õàðàêòåðèñòèê ïåðâè÷íûõ ìàòðèö ôîðìàëè-
çîâàííûì ìåòîäîì. Òàê, êîýôôèöèåíò äîñòóïíîñòè, õàðàêòåðèçóþùèé ðå-
ìîíòíóþ òåõíîëîãè÷íîñòü êîíñòðóêöèè ñáîðî÷íîé åäèíèöû, è êîýôôèöè-
åíò ïîìåõ â ñîîòâåòñòâèè ñ ôîðìóëàìè (6.62) è (6.64)
( ) ( )
K
x
x
N
M
Ê
y
y
N
M
ä
i
i
N
i
i
N
ï
i
i
N
i
i
N
= -
-
= =
-
= -
=
=
=
=
å
å
å
å
1
1 1
1
1
1
1
1
, . (6.94)

59
Êîýôôèöèåíòû (6.94) õàðàêòåðèçóþò ïðîòèâîïîëîæíûå ñòîðîíû ðå-
ìîíòíîé òåõíîëîãè÷íîñòè ñáîðî÷íîé åäèíèöû: Ê
ä
= 1–Ê
ï
. Èíà÷å ãîâîðÿ,
÷åì ëó÷øå äîñòóïíîñòü è âûøå êîýôôèöèåíò Ê
äi
, òåì ìåíüøå ïîìåõ ñîç-
äàþò ïîïóòíûå îïåðàöèè ïðè ðåìîíòå äàííîãî óçëà, è íàîáîðîò. Ñëåäóåò
èìåòü â âèäó, ÷òî äëÿ äåòàëåé Ê
ä
¹ 1 – Ê
ï
.
Ëèòåðàòóðà
1. Íàäåæíîñòü è ýôôåêòèâíîñòü â òåõíèêå: Ñïðàâî÷íèê:  10 ò. Ò.5. Ïðîåêòíûé
àíàëèç íàäåæíîñòè. - Ì.: Ìàøèíîñòðîåíèå, 1988.- 316 ñ.
2. ÃÎÑÒ 2.103-68. ÅÑÊÄ. Ñòàäèè ðàçðàáîòêè.
3. Êóáàðåâ À.È. Íàäåæíîñòü â ìàøèíîñòðîåíèè.- Ì.: Èçä-âî ñòàíäàðòîâ,1989.- 224 ñ.
4. Êàíàð÷óê Â.Å. Îñíîâû íàäåæíîñòè ìàøèí.- Êèåâ: Íàóêîâà äóìêà, 1982.- 248 ñ.
5. Áåðäè÷åâñêèé Á.Å. Âîïðîñû îáåñïå÷åíèÿ íàäåæíîñòè ðàäèîýëåêòðîííîé àïïàðà-
òóðû ïðè ðàçðàáîòêå.- Ì.: Ñîâ.ðàäèî, 1977.- 384 ñ.
6. Ñîòñêîâ Á.Ñ. Îñíîâû òåîðèè è ðàñ÷åòà íàäåæíîñòè ýëåìåíòîâ è óñòðîéñòâ àâòî-
ìàòèêè è âû÷èñëèòåëüíîé òåõíèêè.- Ì.: Âûñø.øêîëà, 1970.- 272 ñ.
7. Êîíäðàøêîâà Ã.À., Ôåñåíêî Å.Ï. Íàäåæíîñòü èçìåðèòåëüíûõ óñòðîéñòâ â öåë-
ëþëîçíî-áóìàæíîé ïðîìûøëåííîñòè.- Ì.: Ëåñíàÿ ïðîìûøëåííîñòü, 1978.- 160 ñ.
8. ÃÎÑÒ 27.003-90. Íàäåæíîñòü â òåõíèêå. Ñîñòàâ è îáùèå ïðàâèëà çàäàíèÿ òðåáî-
âàíèé ïî íàäåæíîñòè.
9. Ñåâåðöåâ Í.À. Íàäåæíîñòü ñëîæíûõ ñèñòåì â ýêñïëóàòàöèè è îòðàáîòêå.- Ì.:
Âûñø.øêîëà, 1989.- 432 ñ.
10. Êàôàðîâ Â.Â. è äð. Îáåñïå÷åíèå è ìåòîäû îïòèìèçàöèè íàäåæíîñòè õèìè÷åñêèõ
è íåôòåïåðåðàáàòûâàþùèõ ïðîèçâîäñòâ.- Ì.: Õèìèÿ, 1987.-272 ñ.
11. Õàçîâ Á.Ô., Äèäóñåâ Á.À. Ñïðàâî÷íèê ïî ðàñ÷åòó íàäåæíîñòè ìàøèí íà ñòàäèè
ïðîåêòèðîâàíèÿ.- Ì.: Ìàøèíîñòðîåíèå, 1986.- 224 ñ.
12. Òðóõàíîâ Â.Ì. Ìåòîäû îáåñïå÷åíèÿ íàäåæíîñòè èçäåëèé ìàøèíîñòðîåíèÿ.- Ì.:
Ìàøèíîñòðîåíèå, 1995.- 304 ñ.
13. Æèëèíñêèé È.Á. Íàäåæíîñòü îáîðóäîâàíèÿ õèìè÷åñêèõ ïðîèçâîäñòâ.- Ì.:
Ìîñê.èí-ò õèìè÷.ìàøèíîñòð., 1981.- 44 ñ.
14. Çóáîâà À.Ô. Íàäåæíîñòü ìàøèí è àïïàðàòîâ õèìè÷åñêèõ ïðîèçâîäñòâ.- Ë.: Ìà-
øèíîñòðîåíèå, 1978.- 214 ñ.
15. Ãðåáåíèê Â.Ì., Öàïêî Â.Ê. Íàäåæíîñòü ìåòàëëóðãè÷åñêîãî îáîðóäîâàíèÿ.
Ñïðàâî÷íèê.- Ì.: Ìåòàëëóðãèÿ, 1980.- 344 ñ.
16. Äðóæèíèí Ã.Â. Íàäåæíîñòü àâòîìàòèçèðîâàííûõ ñèñòåì.- Ì.: Ýíåðãèÿ, 1977.-
536 ñ.
17. Ðÿáèíèí È.À. Îñíîâû òåîðèè è ðàñ÷åòà íàäåæíîñòè ñóäîâûõ ýëåêòðîýíåðãåòè÷å-
ñêèõ ñèñòåì.- Ë.: Ñóäîñòðîåíèå, 1971.- 456 ñ.
18. Êóçüìèí Ô.È. Çàäà÷è è ìåòîäû îïòèìèçàöèè ïîêàçàòåëåé íàäåæíîñòè- Ì.:
Ñîâ.ðàäèî, 1972.- 224 ñ.
19. Ìåòîäèêà âûáîðà íîðì íàäåæíîñòè òåõíè÷åñêèõ óñòðîéñòâ.- Ì.: Èçä-âî ñòàíäàð-
òîâ, 1971.- 32 ñ.
20. Ôåäîòîâ Í.Ô. Ïðèìåíåíèå ñòðóêòóðíîãî è ñòàòèñòè÷åñêîãî àíàëèçà ïðè ïðîåê-
òèðîâàíèè äîðîæíûõ è çåìëåðîéíûõ ìàøèí ñ çàäàííûìè ïîêàçàòåëÿìè íàäåæíîñòè.-
Ñòðîèòåëüíûå è äîðîæíûå ìàøèíû, 1978, ¹ 9, ñ.30-31.
21. ÃÎÑÒ 27.301-83. Íàäåæíîñòü â òåõíèêå. Ïðîãíîçèðîâàíèå íàäåæíîñòè èçäåëèé
ïðè ïðîåêòèðîâàíèè.
22. ÃÎÑÒ 21623-76. Ñèñòåìà òåõíè÷åñêîãî îáñëóæèâàíèÿ è ðåìîíòà òåõíèêè. Ïîêà-
çàòåëè äëÿ îöåíêè ðåìîíòîïðèãîäíîñòè. Òåðìèíû è îïðåäåëåíèÿ.
23. Êóãåëü Ð.Â. Íàäåæíîñòü ìàøèí ìàññîâîãî ïðîèçâîäñòâà.- Ì.: Ìàøèíîñòðîåíèå,
1981.- 244ñ.
24. Õàçîâ Á.Ô. Íàäåæíîñòü ñòðîèòåëüíûõ è äîðîæíûõ ìàøèí.- Ì.: Ìàøèíîñòðîåíèå,
1979.- 192 ñ.
25. Ðåìîíòîïðèãîäíîñòü ìàøèí. Ïîä ðåä.Ï.Í.Âîëêîâà.- Ì.: Ìàøèíîñòðîåíèå,
1975.- 368 ñ.
60
Глава 7
ЭКСПЛУАТАЦИЯ И РЕМОНТ ТЕХНИЧЕСКИХ СИСТЕМ
Ýêñïëóàòàöèÿ èëè èñïîëüçîâàíèå ïî íàçíà÷åíèþ - ñàìûé äëèòåëüíûé è
îòâåòñòâåííûé ïåðèîä â æèçíåííîì öèêëå òåõíè÷åñêîãî îáúåêòà, â òå÷å-
íèå êîòîðîãî îí èñïûòûâàåò íàãðóçêè ðàçëè÷íîãî âèäà è íàõîäèòñÿ ïîä
âîçäåéñòâèåì âíåøíèõ óñëîâèé. Â ïðîöåññå ýêñïëóàòàöèè ïðîâåðÿþòñÿ
òåõíîëîãèè, ìåòîäû è ïðèåìû, èñïîëüçîâàâøèåñÿ íà âñåõ ïðåäûäóùèõ ýòà-
ïàõ, âûÿâëÿþòñÿ èõ íåäîñòàòêè, ïðîÿâëÿþòñÿ ñêðûòûå äåôåêòû êîíñòðóê-
öèîííûõ ìàòåðèàëîâ, ïîãðåøíîñòè èçãîòîâëåíèÿ, ñáîðêè è ìîíòàæà.
Ýêñïëóàòàöèÿ òåõíè÷åñêîé ñèñòåìû - íåïðåðûâíûé ïðîöåññ, òðåáóþùèé
ïëàíîâîãî è ðåãóëÿðíîãî êîíòðîëÿ è âîçäåéñòâèÿ íà ñèñòåìó â öåëîì èëè
íà åå ñîñòàâëÿþùèå è ýëåìåíòû, ÷òî äîëæíî îáåñïå÷èâàòü åå ðàáî÷åå ñî-
ñòîÿíèå è âûñîêèé óðîâåíü ýêñïëóàòàöèîííîé íàäåæíîñòè. Ïîýòîìó ïîä
òåõíè÷åñêîé ýêñïëóàòàöèåé â øèðîêîì ñìûñëå ïîíèìàåòñÿ íå òîëüêî èñ-
ïîëüçîâàíèå îáúåêòà ïî íàçíà÷åíèþ, íî è îáåñïå÷åíèå èñïðàâíîãî ñîñòîÿ-
íèÿ ñ âûñîêèì óðîâíåì íàäåæíîñòè, âêëþ÷àÿ ïëàíîâîå òåõíè÷åñêîå îá-
ñëóæèâàíèå è ðåìîíòû, âîññòàíîâëåíèå ðàáîòîñïîñîáíîñòè ïîñëå îòêàçîâ,
õðàíåíèå, ïîäãîòîâêó ê ðàáîòå è äðóãèå ðàáîòû [1].
7.1. Надежность технических систем при эксплуатации
Êàæäàÿ òåõíè÷åñêàÿ ñèñòåìà â ïðîöåññå ýêñïëóàòàöèè ïðîõîäèò íå-
ñêîëüêî ïåðèîäîâ è, ñîîòâåòñòâåííî, íàõîäèòñÿ â íåñêîëüêèõ ðàçëè÷íûõ
ñîñòîÿíèÿõ:
- èñïîëüçîâàíèå ïî íàçíà÷åíèþ - íåïîñðåäñòâåííîå ñîçäàíèå ïðîäóê-
öèè èëè ïîëó÷åíèå äðóãîãî ïîëîæèòåëüíîãî ýôôåêòà;
- îïåðàòèâíîå òåõíè÷åñêîå îáñëóæèâàíèå - òåõíè÷åñêîå îáñëóæèâà-
íèå ïðè èñïîëüçîâàíèè, íåïîñðåäñòâåííî ïåðåä èëè ïîñëå èñïîëüçîâàíèÿ
(çàïðàâêà òîïëèâîì, îñìîòð, óñòðàíåíèå ìåëêèõ íåèñïðàâíîñòåé è ò.ä.);
- ïåðèîäè÷åñêîå (ïðîôèëàêòè÷åñêîå) òåõíè÷åñêîå îáñëóæèâàíèå -
áîëåå òðóäîåìêîå òåõíè÷åñêîå îáñëóæèâàíèå ïîñëå îïðåäåëåííîé íàðàáîò-
êè èëè ïî äîñòèæåíèè çàäàííûõ çíà÷åíèé ïàðàìåòðîâ (ïî òåõíè÷åñêîìó
ñîñòîÿíèþ);
- ðåìîíò - õàðàêòåðèçóåòñÿ çíà÷èòåëüíîé òðóäîåìêîñòüþ ïî ñðàâíåíèþ
ñ òåõíè÷åñêèì îáñëóæèâàíèåì, ïðè ðåìîíòå òåõíè÷åñêàÿ ñèñòåìà íå èñ-
ïîëüçóåòñÿ ïî íàçíà÷åíèþ äîâîëüíî äëèòåëüíîå âðåìÿ (â çàâèñèìîñòè îò
ïðè÷èí, ñëîæíîñòè è òðóäîåìêîñòè ðàçëè÷àåòñÿ íåñêîëüêî âèäîâ ðåìîíòà);
- ïðîñòîé - ïåðèîä, êîãäà òåõíè÷åñêàÿ ñèñòåìà íàõîäèòñÿ â ðàáîòîñïî-
ñîáíîì ñîñòîÿíèè, íî íå èñïîëüçóåòñÿ ïî íàçíà÷åíèþ, èëè íàõîäèòñÿ â
íåðàáîòîñïîñîáíîì ñîñòîÿíèè, íî íå ðåìîíòèðóåòñÿ ïî êàêèì-ëèáî îðãàíè-
çàöèîííî-òåõíè÷åñêèì è äðóãèì ïðè÷èíàì (â çàâèñèìîñòè îò ñîñòîÿíèÿ
ñèñòåìû è ïðè÷èí ðàçëè÷àåòñÿ íåñêîëüêî âèäîâ ïðîñòîÿ).
