Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 2

Подождите немного. Документ загружается.

181

Ïîñëå èñïûòàíèé âòîðîé âûáîðêè n

íàõîäèòñÿ âûáîðî÷íàÿ õàðàêòåðè-

ñòèêà äëÿ ïîëíîãî îáúåìà èñïûòàíèé R*(n

) è ïðèíèìàåòñÿ îäíà èç

ãèïîòåç èç óñëîâèé:

- ïðè R*(n

)³ R

ïá

ïðèíèìàåòñÿ ãèïîòåçà H

- ïðè R*(n

)< R

ïá

- ïðèíèìàåòñÿ ãèïîòåçà H

, (9.50)

Çíàêè íåðàâåíñòâ â óñëîâèÿõ (9.49) è (9.50) çàâèñÿò îò òîãî, ïî êàêîìó

èç ïîêàçàòåëåé êîíòðîëèðóåòñÿ íàäåæíîñòü.

Ïðè ïëàíèðîâàíèè êîíòðîëÿ ìåòîäîì äâóêðàòíîé âûáîðêè ñíà÷àëà îï-

ðåäåëÿåòñÿ ïîëíûé îáúåì èñïûòàíèé n=n

è ïðèåìî÷íî-áðàêîâî÷íûé

íîðìàòèâ R

ïá

àíàëîãè÷íî ìåòîäó îäíîêðàòíîé âûáîðêè, çàòåì çàäàåòñÿ

îáúåì ïåðâîé âûáîðêè n

è âû÷èñëÿåòñÿ ïðèåìî÷íûé è áðàêîâî÷íûé íîð-

ìàòèâû ïî òåì æå óðàâíåíèÿì, íî (ïîñêîëüêó n

íàçíà÷åíî ïðîèçâîëüíî)

ïðè ýòîì â óñëîâèÿõ (9.49) R

ïð1

¹R

áð1

. Òàê, ïðèåìî÷íûé óðîâåíü R

ïð1

âû-

÷èñëÿåòñÿ ïî ôîðìóëàì äëÿ R

ïð

, ñîäåðæàùèì ðèñê çàêàç÷èêà b è âåëè÷èíó

, à áðàêîâî÷íûé óðîâåíü R

áð1

- ïî ôîðìóëàì R

ïð

, ñîäåðæàùèì a è R

Ïðèìåð 9.11. Ïî óñëîâèÿì ïðèìåðà 9.5 ñïëàíèðîâàòü êîíòðîëü ìåòîäîì äâóêðàòíîé

âûáîðêè, ÷òîáû ïåðâàÿ âûáîðêà ñîñòàâèëà ïðèìåðíî 1/5 îò îáúåìà èñïûòàíèé.

Èç ðåøåíèÿ ïðèìåðà 9.5 n=(n

)=41 è T

ïá

=80,5 ÷. Òîãäà n

» n/5 » 8, n

= 33.

Ïî óðàâíåíèþ (9.24) ïðèåìî÷íûé è áðàêîâî÷íûé óðîâíè äëÿ ïåðâîé âûáîðêè

( ) ()

67235

987

100

100931

= =

c c

Ñëåäîâàòåëüíî, åñëè ïðè èñïûòàíèÿõ n

=8 èçäåëèé ïî ïëàíó [n

,U,n

] ïîëó÷èì

ñðåäíþþ âûáîðî÷íóþ íàðàáîòêó T*(8) ³ 98,7, ïàðòèÿ ïðèíèìàåòñÿ, åñëè T*(8) £ 58 -

áðàêóåòñÿ, åñëè 58<T*(8)<98,7 - áåðåòñÿ âòîðàÿ âûáîðêà îáúåìîì n

=33. Ïîñëå åå èñ-

ïûòàíèé ïðèíèìàåòñÿ îêîí÷àòåëüíîå ðåøåíèå: ïàðòèÿ ïðèíèìàåòñÿ ïðè T*(41)³80,5 è

áðàêóåòñÿ ïðè T*(41)<80,5.

Âåëè÷èíà îòíîñèòåëüíîãî îáúåìà ïåðâîé âûáîðêè n

/(n

) îïðåäå-

ëÿåò âåëè÷èíó "çîíû íåîïðåäåëåííîñòè" îò R

ïð1

äî R

áð1

: ñ óâåëè÷åíèåì n

ýòà îáëàñòü ñóæàåòñÿ (â ïðåäåëå ïðè n

=n äî íóëÿ) è íàîáîðîò. Òàê ÷òî

÷åì ìåíüøèì áóäåò íàçíà÷åí îáúåì ïåðâîé âûáîðêè n

, òåì áîëüøå âîç-

ìîæíàÿ ýêîíîìèÿ çàòðàò íà èñïûòàíèÿ, íî òåì ñ ìåíüøåé âåðîÿòíîñòüþ

òàêàÿ âîçìîæíîñòü áóäåò ðåàëèçîâàíà. Îáû÷íûå çíà÷åíèÿ îòíîñèòåëüíîãî

îáúåìà ïåðâîé âûáîðêè n

/(n

) - îò 0,2 äî 0,5.

Åñëè îáùèé îáúåì èñïûòàíèé n, íåîáõîäèìûé ïî ìåòîäó îäíîêðàòíîé

âûáîðêè, ðàçáèòü íà áîëüøåå êîëè÷åñòâî äèñêðåòíûõ âûáîðîê, ñîîòâåòñò-

âåííî ìîæíî ñïëàíèðîâàòü èñïûòàíèÿ ïî ìåòîäó òðåõ-, ÷åòûðåõ-, è ò.ä.

êðàòíûõ âûáîðîê. Ïðè ýòîì äëÿ âñåõ ïðîìåæóòî÷íûõ ýòàïîâ ïëàíèðóþòñÿ

ðàçäåëüíî ïðèåìî÷íûé è áðàêîâî÷íûé íîðìàòèâû, à èñõîä èñïûòàíèé ïðè-

íèìàåòñÿ ïî óñëîâèÿì (9.49).

Ïðè ïëàíèðîâàíèè òàêèì îáðàçîì, ÷òîáû â êàæäîé èç äèñêðåòíûõ âû-

áîðîê ñîäåðæàëîñü òîëüêî îäíî èñïûòàíèå ìåòîä ìíîãîêðàòíûõ âûáîðîê

ïðàêòè÷åñêè ïåðåõîäèò â ìåòîä ïîñëåäîâàòåëüíîãî êîíòðîëÿ.

182

9.2. Метод последовательного контроля

Äëÿ îáîñíîâàííîãî âûáîðà ãèïîòåç ïî êðèòåðèþ Íåéìàíà-Ïèðñîíà òðå-

áóåòñÿ èñïûòàíèå ïîëíîãî îáúåìà âûáîðêè n, óñòàíîâëåííîãî ïðè ïëàíè-

ðîâàíèè. Îäíàêî ïàðòèè ñ î÷åíü íèçêèì èëè âûñîêèì óðîâíåì íàäåæíîñòè

ïî ñðàâíåíèþ ñ çàäàííûìè R

è R

÷àñòî ìîæíî âûÿâèòü è ïðè ìåíüøåì

êîëè÷åñòâå èñïûòàíèé. Âîçìîæíîñòü àðãóìåíòèðîâàííîé êâàëèôèêàöèè

ïàðòèè áåç ïðåäâàðèòåëüíîé ôèêñàöèè îáúåìà èñïûòàíèé n äàåò èñïîëüçî-

âàíèå ïîñëåäîâàòåëüíîãî êðèòåðèÿ ïðîâåðêè ãèïîòåç èëè êðèòåðèÿ Âàëüäà.

Ïî ýòîìó êðèòåðèþ ïðîâåðêà ãèïîòåç ìîæåò áûòü íà÷àòà ïðè ëþáîì îáúå-

ìå âûáîðêè n (â òîì ÷èñëå n=1), à îáîñíîâàííîå ðåøåíèå î ïðèåìêå èëè

áðàêîâêå ïðèíèìàåòñÿ, êîãäà ðåçóëüòàòû ýêñïåðèìåíòà äîñòàòî÷íî äîñòî-

âåðíî (ïî ñðàâíåíèþ ñ çàäàííûìè âåëè÷èíàìè âåðîÿòíîñòåé îøèáîê a è

b) ïîêàçûâàþò ïðåîáëàäàíèå îäíîé èç ãèïîòåç.

Òåîðåòè÷åñêîé îñíîâîé ìåòîäà ÿâëÿåòñÿ êðèòåðèé Âàëüäà, ñîãëàñíî êî-

òîðîìó äëÿ âûáîðà îäíîé èç ãèïîòåç î íàäåæíîñòè ïðè èññëåäîâàíèè âûáî-

ðî÷íîé ñîâîêóïíîñòè ïðîèçâîëüíîãî îáúåìà n âû÷èñëÿåòñÿ îòíîøåíèå ïðàâ-

äîïîäîáèÿ - îòíîøåíèå âåðîÿòíîñòåé [1,2,8-10]. Ïðè âûïîëíåíèè óñëîâèé

ïðèåìêè èëè áðàêîâêè èñïûòàíèÿ çàêàí÷èâàþòñÿ, à â ñëó÷àå íåîïðåäåëåí-

íîñòè èñïûòûâàåòñÿ äîïîëíèòåëüíîå êîëè÷åñòâî èçäåëèé è ïðîöåññ ïðîâåð-

êè ïîâòîðÿåòñÿ äî òåõ ïîð, ïîêà ïàðòèÿ áóäåò ïðèíÿòà èëè çàáðàêîâàíà.

Ïðîäîëæèòåëüíîñòü ïîñëåäîâàòåëüíîãî êîíòðîëÿ - ñëó÷àéíàÿ âåëè÷èíà,

ïîýòîìó òðåáóåìûé îáúåì íàáëþäåíèé â íåêîòîðûõ ñëó÷àÿõ ìîæåò ïðåâû-

ñèòü îáúåì èñïûòàíèé, äîñòàòî÷íûé äëÿ îäíîñòóïåí÷àòîãî êîíòðîëÿ. Â ñâÿ-

çè ñ ýòèì ÷àñòî èñïîëüçóåòñÿ óñå÷åííûé ïîñëåäîâàòåëüíûé ìåòîä êîíòðîëÿ.

9.2.1. Критерий Вальда

Ôîðìóëèðîâêà ãèïîòåç ïî êðèòåðèþ Âàëüäà íåñêîëüêî îòëè÷àåòñÿ îò

óñëîâèé ïðîâåðêè ïî êðèòåðèþ Íåéìàíà-Ïèðñîíà:

- ïðÿìàÿ ãèïîòåçà H

(íàäåæíîñòü ïàðòèè ñîîòâåòñòâóåò òðåáîâàíè-

ÿì): R

= R

;

- îáðàòíàÿ (àëüòåðíàòèâíàÿ) ãèïîòåçà H

(íàäåæíîñòü ïàðòèè íå

ñîîòâåòñòâóåò òðåáîâàíèÿì): R

= R

Áóäåì ñ÷èòàòü, ÷òî ïðè íåêîòîðîì îáúåìå èñïûòàíèé n ïîëó÷åíà âûáî-

ðî÷íàÿ ñîâîêóïíîñòü ñëó÷àéíîãî ïîêàçàòåëÿ íàäåæíîñòè R. Ïëîòíîñòü âå-

ðîÿòíîñòè, îïèñûâàþùàÿ âûáîðî÷íîå ðàñïðåäåëåíèå, ÿâëÿåòñÿ óñëîâíîé,

ïîñêîëüêó çàâèñèò îò âåëè÷èíû ãåíåðàëüíîãî ïàðàìåòðà R

. Ìîæíî ââåñòè

ïëîòíîñòè âåðîÿòíîñòè f(R/R

) è f(R/R

), îòâå÷àþùèå ïðîâåðÿåìûì ãè-

ïîòåçàì Í

è Í

. Èõ çíà÷åíèÿ, âû÷èñëåííûå äëÿ ëþáîãî çíà÷åíèÿ R

èç

âûáîðî÷íîé ñîâîêóïíîñòè, áóäóò òåì áîëüøå, ÷åì âåðîÿòíåå âåëè÷èíà R

äëÿ ïðåäïîëàãàåìûõ çíà÷åíèé R

è R

Äëÿ âñåé âûáîðî÷íîé ñîâîêóïíîñòè ìîæíî âû÷èñëèòü ñîâìåñòíóþ óñ-

ëîâíóþ ïëîòíîñòü âåðîÿòíîñòè ïî òåîðåìå óìíîæåíèÿ âåðîÿòíîñòåé äëÿ

íåçàâèñèìûõ ñîáûòèé:

183

(

)

fRR R R fR R

ô1 2

, ,... / ( / )=

. (9.51)

Ïðîèçâåäåíèå (9.51) ïîêàçûâàåò âåðîÿòíîñòü âûïîëíåíèÿ ïðåäïîëîæå-

íèÿ î âåëè÷èíå ïàðàìåòðà ðàñïðåäåëåíèÿ R

â âûáîðêå (è ãåíåðàëüíîé

ïàðòèè) è íàçûâàåòñÿ ôóíêöèåé ïðàâäîïîäîáèÿ:

fR R R PH fR R R PH

ô i

( / ) ( ), ( / ) ( )

Õ Õ

= = = =

0 0

1 1

. (9.52)

Îòíîøåíèå ïðàâäîïîäîáèÿ (ïîñëåäîâàòåëüíûé êðèòåðèé îòíîøåíèÿ âå-

ðîÿòíîñòåé) [1,2,8,10,11]

( )

fR R R

i ô

i ôi

(9.53)

ïîêàçûâàåò, âî ñêîëüêî ðàç â âûáîðêå (è, ñîîòâåòñòâåííî, â ïàðòèè) áîëåå

âåðîÿòíà ãèïîòåçà H

, ÷åì H

. Ýòî îòíîøåíèå ìîæåò áûòü âû÷èñëåíî äëÿ

âûáîðêè ëþáîãî îáúåìà n è ó÷èòûâàåò âñå íàáëþäåíèÿ. Ìàëûå çíà÷åíèÿ

êðèòåðèÿ Ï óêàçûâàþò íà áîëüøåå ïðàâäîïîäîáèå ãèïîòåçû Í

, ïîýòîìó

ïðè äîñòàòî÷íî ìàëîé âåëè÷èíå Ï ïàðòèÿ äîëæíà ïðèíèìàòüñÿ. Êðèòè÷å-

ñêèì ïðèåìî÷íûì óðîâíåì À ÿâëÿåòñÿ îòíîøåíèå âåðîÿòíîñòåé ïðèåìêè

íåãîäíîé è ãîäíîé ïàðòèè, à óñëîâèå ïðèåìêè èìååò âèä:

fR R R

i ô

= £ = =

( / )

( )

0 1

0 0

. (9.54)

Âûïîëíåíèå íåðàâåíñòâà (9.54) îçíà÷àåò, ÷òî âûáîðî÷íàÿ ñîâîêóïíîñòü

óêàçûâàåò íà ïðåîáëàäàíèå ãèïîòåçû H

â áîëüøåé ìåðå, ÷åì ýòî òðåáóåò-

ñÿ çàäàííûìè ðèñêàìè èçãîòîâèòåëÿ a è çàêàç÷èêà b.

Àíàëîãè÷íî ðàññóæäàÿ, ìîæíî ââåñòè êðèòè÷åñêèé áðàêîâî÷íûé óðî-

âåíü B îòíîøåíèÿ ïðàâäîïîäîáèÿ è ñôîðìóëèðîâàòü óñëîâèå áðàêîâêè

(âûáîðà ãèïîòåçû H

fR R R

i ô

= ³ = =

( / )

( )

1 1

1 0

1 b

. (9.55)

Åñëè íè îäíî èç íåðàâåíñòâ (9.54) è (9.55) íå âûïîëíÿåòñÿ, çíà÷èò ïðè

èìåþùåìñÿ îáúåìå èñïûòàíèé íå ïîäòâåðæäàåòñÿ â äîñòàòî÷íîé ìåðå ïðå-

îáëàäàíèå íè îäíîé èç ãèïîòåç H

è H

. Ñîîòâåòñòâåííî, óñëîâèå íåîïðå-

äåëåííîñòè, òðåáóþùåå ïðîäîëæåíèÿ èñïûòàíèé è óâåëè÷åíèÿ îáúåìà âû-

áîðêè n, çàïèñûâàåòñÿ â âèäå [3]:

= < =

< =

A Ï

fR R R

i ô

( / )

. (9.56)

Âûðàæåíèÿ (9.54)-(9.56) ÿâëÿþòñÿ ôîðìóëèðîâêîé êðèòåðèÿ Âàëüäà.

Îáúåì íàáëþäåíèé n óâåëè÷èâàåòñÿ äî òåõ ïîð, ïîêà âûïîëíÿåòñÿ óñëîâèå

184

(9.56). Èñïûòàíèÿ ïðåêðàùàþòñÿ, êîãäà âûïîëíÿòñÿ óñëîâèÿ (9.54) èëè

(9.55) è, ñîîòâåòñòâåííî, ïðèíèìàåòñÿ ãèïîòåçà Í

èëè Í

. Ïðîâåðêà ãè-

ïîòåç ìîæåò áûòü íà÷àòà ïðè ñêîëü óãîäíî ìàëîì îáúåìå èñïûòàíèé n,

÷òî ïîçâîëÿåò áûñòðî âûÿâèòü âûñîêîíàäåæíûå èëè, íàîáîðîò, íèçêîíà-

äåæíûå ïàðòèè èçäåëèé.

Ñðàâíèòåëüíûé àíàëèç ïîêàçûâàåò, ÷òî ïðèìåíåíèå ìåòîäà ïîñëåäîâà-

òåëüíîãî àíàëèçà â ñðåäíåì îáåñïå÷èâàåò ñîêðàùåíèå îáúåìà èñïûòàíèé â

íåñêîëüêî ðàç ïî ñðàâíåíèþ ñ ìåòîäîì îäíîêðàòíîé âûáîðêè. Íàïðèìåð,

ïðè ðèñêå çàêàç÷èêà b=0,1 îáúåì èñïûòàíèé ñîêðàùàåòñÿ ïðèìåðíî â 6

ðàç, à ïðè b=0,01 - â 5 ðàç [8].

Äëÿ íåêîòîðûõ êîíêðåòíûõ ïîêàçàòåëåé íàäåæíîñòè è çàêîíîâ ðàñïðå-

äåëåíèÿ ïðîöåäóðó ïðèíÿòèÿ ðåøåíèÿ óäàåòñÿ óïðîñòèòü, èñêëþ÷èâ âû-

÷èñëåíèå âåëè÷èíû Ï. Êðîìå òîãî, ðåøåíèå çàäà÷è ñóùåñòâåííî óïðîùà-

åòñÿ ïðè ïîñòðîåíèè ãðàôè÷åñêèõ çàâèñèìîñòåé êðèòè÷åñêèõ ïðèåìî÷íîãî

A è áðàêîâî÷íîãî B óðîâíåé (ëèíèé ïðèåìêè è áðàêîâêè) îò çàäàííûõ ïà-

ðàìåòðîâ ïëàíà êîíòðîëÿ. Ïîðÿäîê ïîñòðîåíèÿ, âèä è âçàèìíîå ðàñïîëî-

æåíèå ãðàôèêîâ çàâèñÿò îò âèäà êîíòðîëèðóåìîãî ïàðàìåòðà.

9.2.2. Последовательный контроль вероятности отказа

Åñëè êîíòðîëèðóåìûì ïîêàçàòåëåì íàäåæíîñòè R

ÿâëÿåòñÿ âåðîÿò-

íîñòü îòêàçà q

)

èëè âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû p(t

)=1-q(t

)) çà

âðåìÿ t

, òî óñëîâèÿ ïðèíÿòèÿ ãèïîòåç èìåþò âèä

: q

) = q

); H

: q

) = q

). (9.57)

Äëÿ èõ ïðîâåðêè àíàëîãè÷íî îäíîñòóïåí÷àòîìó ìåòîäó èñïûòàíèÿ ïðî-

èçâîëüíîãî ÷èñëà èçäåëèé n ïðîâîäÿòñÿ ïî ïëàíó [n,U,t

] è ïîäñ÷èòûâàåò-

ñÿ êîëè÷åñòâî îòêàçàâøèõ èçäåëèé r, êîòîðîå âûñòóïàåò â êà÷åñòâå ñëó-

÷àéíîé âûáîðî÷íîé âåëè÷èíû. Òàêèì îáðàçîì, âûáîðî÷íàÿ ñîâîêóïíîñòü

ñîäåðæèò âñåãî îäèí ýëåìåíò r. Ñîîòâåòñòâåííî, óñëîâíîé ïëîòíîñòüþ âå-

ðîÿòíîñòè f(R

) (9.51) ÿâëÿåòñÿ âåðîÿòíîñòü ïîÿâëåíèÿ r îòêàçîâ â

âûáîðêå îáúåìîì n. Â ñàìîì îáùåì ñëó÷àå ýòà âåðîÿòíîñòü îïèñûâàåòñÿ

ãèïåðãåîìåòðè÷åñêèì ðàñïðåäåëåíèåì, ãäå ãåíåðàëüíûì ïàðàìåòðîì ÿâëÿ-

åòñÿ M

N, à M

N è M

N - åãî êîíòðîëèðóåìûå óðîâíè, ñîîò-

âåòñòâóþùèå ãèïîòåçàì (9.57). Òîãäà óñëîâíûå ïëîòíîñòè âåðîÿòíîñòè ïî-

ÿâëåíèÿ r îòêàçîâ äëÿ ïðîâåðÿåìûõ ãèïîòåç (9.57) çàïèøóòñÿ â âèäå

( ) ( )

Pr q q

C C

Pr q q

C C

/ /= =

= =

0 0

1 1

; . (9.58)

(çäåñü è äàëåå çàâèñèìîñòü âåðîÿòíîñòè îòêàçà îò âðåìåíè äëÿ êðàòêîñòè îïóñêàåòñÿ).

Îòíîøåíèå ïðàâäîïîäîáèÿ (9.53) ïðèìåò âèä

( )

(

)

( )

Pr q q

C C

= =

1 1

0 0

(9.59)

èëè ïðèáëèæåííî

185

M r

» -

, (9.60)

ãäå g =M

–M

Âûðàæåíèÿ (9.59) è (9.60) íå ïîçâîëÿþò ïîëó÷èòü óðàâíåíèÿ ëèíèé

ïðèåìêè A(n) è áðàêîâêè B(n) â êîîðäèíàòàõ (n,r), ïîýòîìó ãðàôèêè

ñòðîÿòñÿ ïî òðåì õàðàêòåðíûì òî÷êàì.

Òî÷êà A - òî÷êà ïåðåñå÷åíèÿ ëèíèè ïðèåìêè A(n) ñ ãîðèçîíòàëüíîé

îñüþ n (ïðè r

=0). Äëÿ íàõîæäåíèÿ àáñöèññû n

íóæíî ïðèðàâíÿòü, ñî-

ãëàñíî (9.56), âûðàæåíèå (9.60) âåëè÷èíå b/(1–a) è ïðè r=0 íàéòè n:

1 1

= -

n N

; . (9.61)

Òî÷êà B - òî÷êà ïåðåñå÷åíèÿ ëèíèè áðàêîâêè B(n) ñ ãîðèçîíòàëüíîé

îñüþ n (ïðè r

=0). Íàõîæäåíèå n

àíàëîãè÷íî:

n N

= -

. (9.62)

Àáñöèññà òðåòüåé òî÷êè C n

=N. Â ýòîì ïðåäåëüíîì ñëó÷àå èñïûòûâà-

åòñÿ âñÿ ïàðòèÿ N, òàê ÷òî íåîïðåäåëåííîñòü è ðèñê â ïðèíÿòèè ãèïîòåç

èñêëþ÷àåòñÿ. Ïðè ýòîì

= (M

+ M

)/2 . (9.63)

Ëèíèè, ñîåäèíÿþùèå òî÷êè À ñ C è Â ñ C - ëèíèè ïðèåìêè è áðàêîâêè.

Â ïðîöåññå èñïûòàíèé ïî çíà÷åíèÿì n è r òî÷êà ñ êîîðäèíàòàìè (n,r)

íàíîñèòñÿ íà ãðàôèê. Äàëüíåéøèå äåéñòâèÿ îïðåäåëÿþòñÿ óñëîâèÿìè:

- r ³ B(n) - áðàêîâêà ïàðòèè (ãèïîòåçà H

);

- r £ A(n) - ïðèåìêà ïàðòèè (ãèïîòåçà H

); (9.64)

- A(n) < r < B(n) - óâåëè÷åíèå îáúåìà èñïûòàíèé.

Ïðèìåð 9.12. Ïîñëåäîâàòåëüíîìó êîíòðîëþ ïîäâåðãàåòñÿ ïàðòèÿ èç N=100 èçäå-

ëèé. Êîíòðîëèðóåìûå óðîâíè âåðîÿòíîñòè îòêàçà q

=0,05 è q

=0,1, ðèñêè èçãîòîâèòåëÿ

è çàêàç÷èêà a=b=0,1. Òðåáóåòñÿ ïîñòðîèòü ïëàí èñïûòàíèé â ãðàôè÷åñêîì âèäå è îöå-

íèòü ïàðòèþ, åñëè äëÿ n=25 èñïûòàííûõ èçäåëèé â òå÷åíèå âðåìåíè, çà êîòîðîå çàäà-

íû âåðîÿòíîñòè q

è q

çàôèêñèðîâàíî r=4 îòêàçà.

Ïîñêîëüêó îáúåìû èñïûòàíèé (n=25) è ïàðòèè (N=100) ñîèçìåðèìû, ÷èñëî îòêàçîâ

ïîä÷èíÿåòñÿ ãèïåðãåîìåòðè÷åñêîìó çàêîíó. Äëÿ íåãî âû÷èñëèì: M

N=5;

N=10; g =M

–M

=5.

Äëÿ ïîñòðîåíèÿ ãðàôèêà êîíòðîëÿ âû÷èñëèì êîîðäèíàòû õàðàêòåðèñòè÷åñêèõ òî÷åê

A, B è C, èñïîëüçóÿ ôîðìóëû (9.61)-(9.63):

r n r n

A A B B

= = -

= = = -

=-0 1001

36 0 1001

15 15

/ /

= N = 100; r

= (5+10)/2 = 7,5.

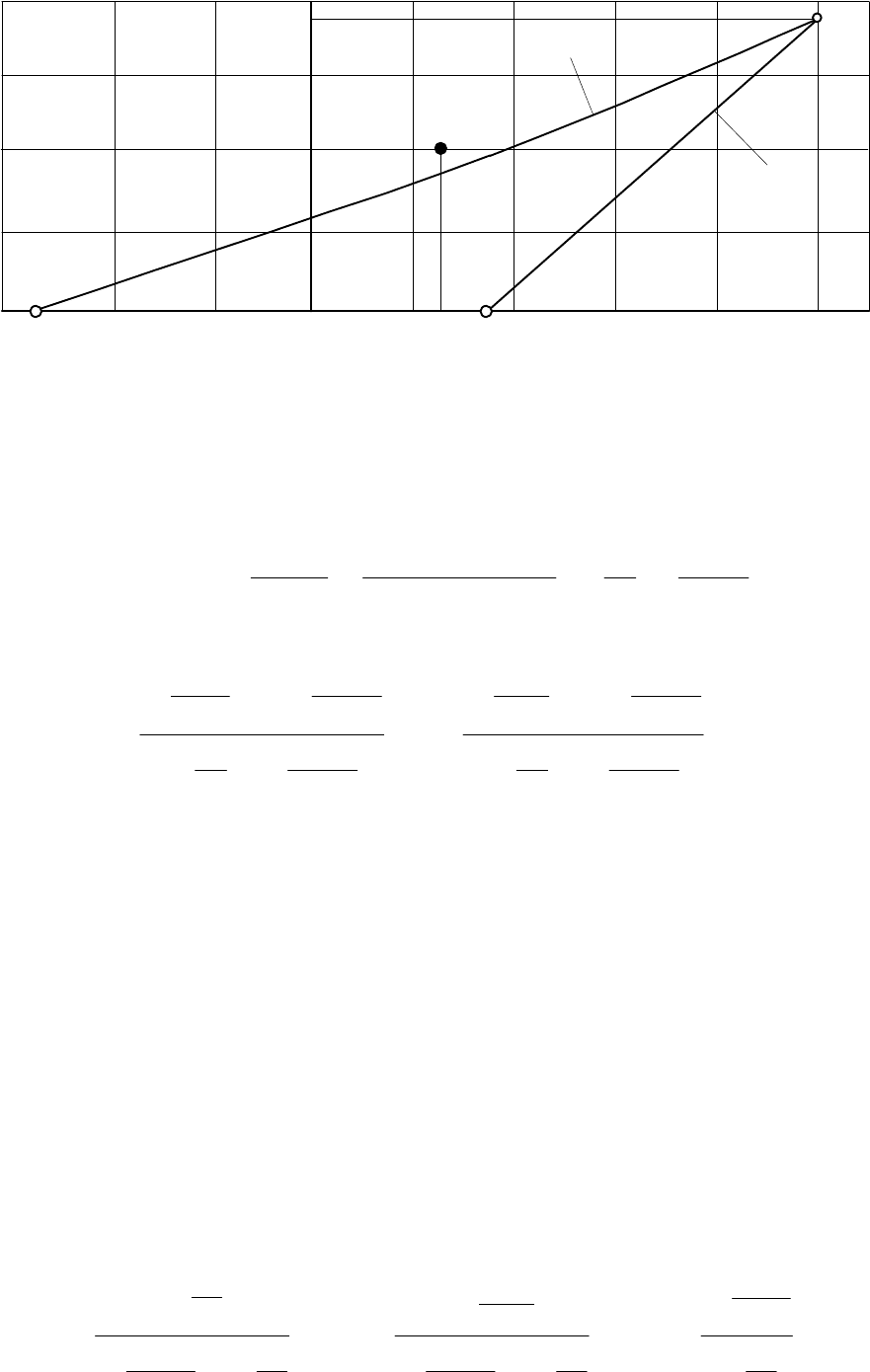
Ãðàôèê êîíòðîëÿ ïðèâåäåí íà ðèñ.9.6. Êðèòåðèé ïðèíÿòèÿ ðåøåíèÿ ïðè ïðîèçâîëü-

íîì n îïðåäåëåí óñëîâèÿìè (9.64).

Òî÷êà, îòâå÷àþùàÿ èñõîäíûì äàííûì (n=25, r=4) íà ðèñ.9.6 íàõîäèòñÿ â îáëàñòè

áðàêîâêè, ñëåäîâàòåëüíî, ñ âåðîÿòíîñòüþ îøèáêè íå áîëåå a=0,1 ñïðàâåäëèâî óòâåð-

æäåíèå, ÷òî íàäåæíîñòü ïàðòèè íèæå òðåáóåìîé (q

>0,1).

186

Ïðè n<0,1N âåðîÿòíîñòü ïîÿâëåíèÿ r îòêàçîâ â âûáîðêå n õîðîøî îïè-

ñûâàåòñÿ áèíîìèàëüíûì ðàñïðåäåëåíèåì. Â ýòîì ñëó÷àå îòíîøåíèå ïðàâ-

äîïîäîáèÿ (9.53):

( )

ÐÍ

Ñq q

r nr

= =

1 1

0 0

. (9.65)

Òîãäà óñëîâèå íåîïðåäåëåííîñòè (9.56) ìîæíî ïðèâåñòè ê âèäó

Bn()

ln ln

()=

< <

. (9.66)

Ëåâàÿ è ïðàâàÿ ÷àñòè íåðàâåíñòâà (9.66) ÿâëÿþòñÿ óðàâíåíèÿìè ëèíèé

ïðèåìêè A(n) è áðàêîâêè B(n). Â ýòîì ñëó÷àå îíè ïàðàëëåëüíû, ïðè÷åì

ëèíèÿ A(n) ñìåùåíà âíèç, à B(n) - ââåðõ îò íà÷àëà êîîðäèíàò, à âåëè÷è-

íû ýòèõ ñìåùåíèé â ïåðâóþ î÷åðåäü îïðåäåëÿþòñÿ çíà÷åíèÿìè ðèñêîâ b è

a. Èç (9.66) ìîæíî çàïèñàòü óñëîâèå ïðèåìêè (H

) è áðàêîâêè (H

r £ A(n) , r ³ B(n). (9.67)

Äëÿ óïðîùåíèÿ ïëàíèðîâàíèÿ ðàçðàáîòàíû òàáëèöû ïëàíèðîâàíèÿ [4,5],

ïî êîòîðûì ëèíèè ïðèåìêè A(n) è áðàêîâêè B(n) ñòðîÿòñÿ â êîîðäèíàòàõ

(n,r) â âèäå ïðÿìûõ ïî óðàâíåíèÿì, ñîîòâåòñòâåííî,

r = a(n - n

), r = an + r

, (9.68)

à êîýôôèöèåíòû óðàâíåíèé (9.68) a, r

è n

ðàññ÷èòàíû â ñîîòâåòñòâèè ñ

óñëîâèÿìè (9.66) èñõîäÿ èç çàäàííûõ çíà÷åíèé a, b, P

=1-q

è P

=1-q

(ïðèë.XI, òàáë.XI.4):

ln ln

(9.69)

A(n)

B(n)

-60 -40 -20 0 20 40 60 80 100

Ðèñ.9.6. Ãðàôèê äëÿ êîíòðîëÿ âåðîÿòíîñòè ïðè ãèïåðãåîìåòðè÷åñêîì ðàñïðåäåëåíèè

(ê ïðèìåðó 9.12).

187

Ïðè a=b r

=an

è óðàâíåíèÿ ïðÿìûõ (9.68) ïðèîáðåòàþò âèä

r = an ± r

. (9.70)

Ñðåäíÿÿ ïðîäîëæèòåëüíîñòü êîíòðîëÿ (ñðåäíåå ÷èñëî íàáëþäåíèé n äî

ïðèíÿòèÿ ðåøåíèÿ î ïðèåìêå ïðè P=P

) îïðåäåëÿåòñÿ ïî ôîðìóëå [4,5]:

( )

ñð

ln ln

.»

- -

1 1

(9.71)

Ïðèìåð 9.13. Äëÿ êîíòðîëÿ íàäåæíîñòè ýëåìåíòîâ çàäàíû äâà óðîâíÿ âåðîÿòíîñòè

áåçîòêàçíîé ðàáîòû ïðè íàðàáîòêå 20 ÷: P

=0,95 è P

=0,90. Íåîáõîäèìî îïðåäåëèòü

ïëàí êîíòðîëÿ íàäåæíîñòè ïîñëåäîâàòåëüíûì ìåòîäîì ïðè ðèñêàõ èçãîòîâèòåëÿ è çà-

êàç÷èêà a=0,05 è b=0,10.

Ïî òàáëèöàì (ïðèë.XI, òàáë.XI.4) èëè ôîðìóëàì (9.69) íàõîäèì êîýôôèöèåíòû ëè-

íèé ïðèåìêè è áðàêîâêè:

a r n=

= =

, ,

095

090

1090

1095

095

090

0072358

1010

005

1090

1095

095

090

387

1005

010

095

090

4164

0 0

Ñ ó÷åòîì ïîëó÷åííûõ çíà÷åíèé ïî ôîðìóëàì (9.68) ñòðîÿòñÿ ëèíèè ïðèåìêè è áðà-

êîâêè (ðèñ.9.7, ïðÿìûå 1 è 2).

Ñðåäíåå ÷èñëî èñïûòàíèé (îáúåì âûáîðêè) äî ïðèåìêè ïî ôîðìóëå (9.71) èëè

òàáë.XI.4 (ïðèë.XI):

( )

ñð

, ln

ln ln

,.»

- -

1005

010

005

1010

005

1194

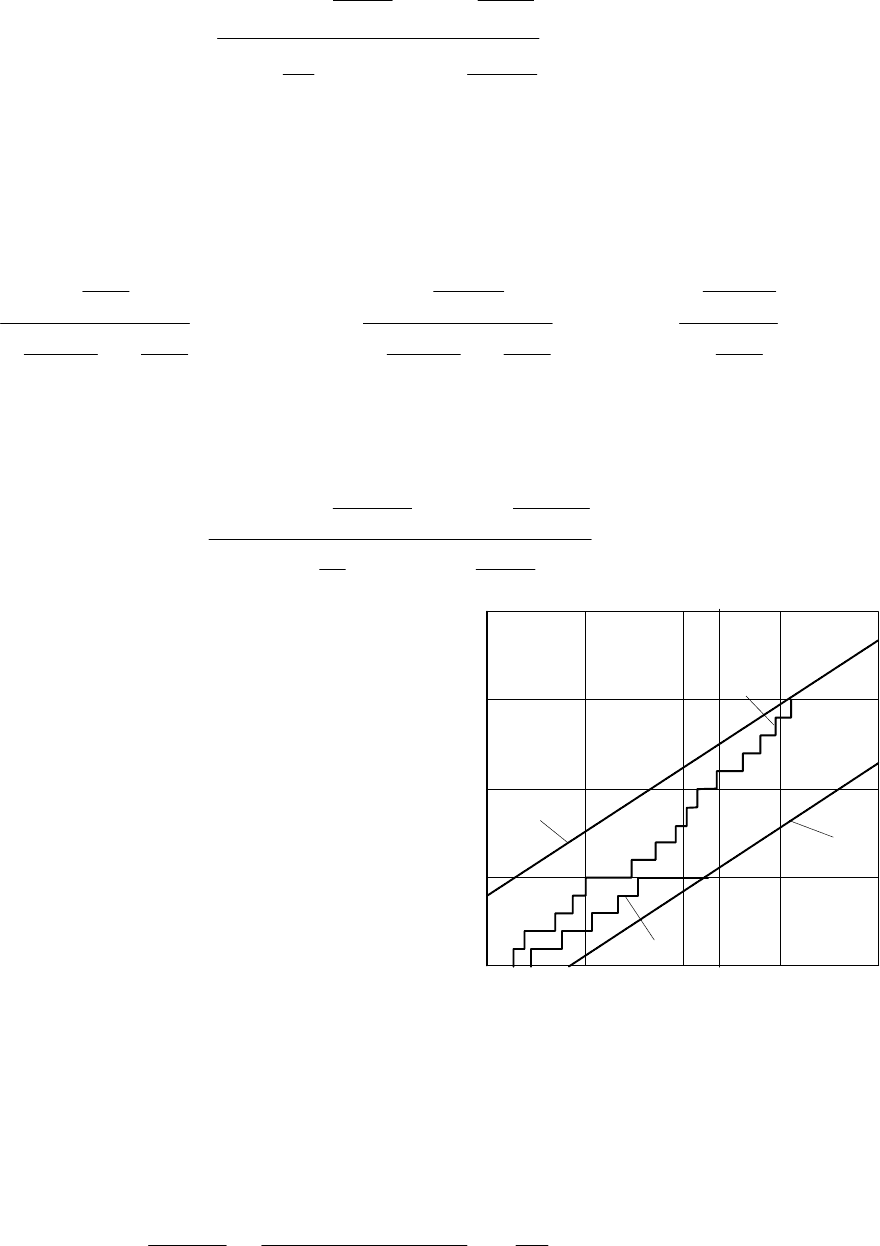
Ïðè êîíòðîëå íåîáõîäèìî îðãàíèçîâàòü â

ñðåäíåì 119,4 öèêëîâ ðàáîòû (äëÿ âîññòà-

íàâëèâàåìûõ ýëåìåíòîâ) èëè èñïûòàíèÿ

119,4 ýëåìåíòîâ (äëÿ íåâîññòàíàâëèâàåìûõ)

äëèòåëüíîñòüþ 20 ÷. Ïî çàâåðøåíèè êàæäîãî

èñïûòàíèÿ ïîäñ÷èòûâàåòñÿ íàêîïëåííîå ÷èñ-

ëî çàêîí÷åííûõ èñïûòàíèé n è íàêîïëåííîå

÷èñëî îòêàçîâ r, íà ãðàôèêå íàíîñÿòñÿ òî÷êè

ñ êîîðäèíàòàìè (n,r), ïî êîòîðûì ñòðîèòñÿ

ñòóïåí÷àòàÿ ëèíèÿ èñïûòàíèé (ðèñ.9.7). Èñ-

ïûòàíèÿ ïðîäîëæàþòñÿ, ïîêà ëèíèÿ ïðîõîäèò

â îáëàñòè íåîïðåäåëåííîñòè ìåæäó ëèíèÿìè

ïðèåìêè 1 è áðàêîâêè 2. Åñëè ëèíèÿ èñïû-

òàíèé ïåðåñåêàåò ëèíèþ ïðèåìêè 1 è ïîïà-

äàåò â îáëàñòü ïðèåìêè H

, òî èçäåëèÿ ïðè-

íèìàþòñÿ, åñëè ëèíèþ áðàêîâêè 2 è ïîïàäà-

åò â îáëàñòü áðàêîâêè H

, òî èçäåëèÿ áðàêó-

þòñÿ. Íà ðèñ.9.7 íàíåñåíû äâå èç âîçìîæíûõ

ðåàëèçàöèé èñïûòàíèé (ëèíèè I è II) - ðåàëè-

çàöèÿ I îçíà÷àåò ïîëîæèòåëüíûé ðåçóëüòàò

èñïûòàíèé, ðåàëèçàöèÿ II - îòðèöàòåëüíûé.

Åñëè ïîìèìî n<0,1N âûïîëíÿåòñÿ óñëîâèå q

£0,1, òî ÷èñëî îòêàçîâ

r ìîæåò áûòü îïèñàíî ðàñïðåäåëåíèåì Ïóàññîíà (ñì.ãë.2). Òîãäà îòíîøå-

íèå ïðàâäîïîäîáèÿ (9.53)

( )

( ) ( )

( )

[ ]

nq nq

nq q

= =

- -

1 1

0 1

1 0

exp

exp . (9.72)

0 50 100 150

ñð

Ðèñ.9.7. Ãðàíèöû îáëàñòåé ïðèåìêè (H

)

è áðàêîâêè (

) (ê ïðèìåðó 9.13)

188

Àíàëîãè÷íî ñëó÷àþ áèíîìèàëüíîãî ðàñïðåäåëåíèÿ ìîæíî ïîëó÷èòü

( )

nq q

+ -

+ -ln

1 0

, . (9.73)

Óñëîâèÿ ïðèíÿòèÿ ðåøåíèÿ îñòàþòñÿ â âèäå (9.66)-(9.67), ëèíèè ïðè-

åìêè A(n) è áðàêîâêè òàêæå ïàðàëëåëüíû B(n).

Ïðèìåð 9.14. Óñòàíîâëåíî ìèíèìàëüíî äîïóñòèìîå çíà÷åíèå âåðîÿòíîñòè ñðàáà-

òûâàíèÿ óñòðîéñòâà p

=0,9 ïðè íîðìàëüíîì çíà÷åíèè p

=0,95. Òðåáóåòñÿ îðãàíèçîâàòü

êîíòðîëü íàäåæíîñòè ïðè a=0,03 è b=0,02..

Ìàêñèìàëüíî äîïóñòèìàÿ âåðîÿòíîñòü îòêàçà (íåñðàáàòûâàíèÿ) q

=1–p

=0,1, íîð-

ìàëüíîå çíà÷åíèå - q

=1–p

=0,05. Ïîñêîëüêó q

è q

íå ïðåâîñõîäÿò 0,1, âîñïîëüçóåìñÿ

ðàñïðåäåëåíèåì Ïóàññîíà è âû÷èñëèì ïî óðàâíåíèÿì (9.73):

A(n)= –5,6 + 0,073n; B(n) = 5,03 + 0,073n.

Ïðè ïðîâåäåíèè êîíòðîëÿ êàæäîãî èçäåëèÿ åãî ïîäâåðãàþò èñïûòàíèþ n ðàç, ïîä-

ñ÷èòûâàÿ ïðè ýòîì ÷èñëî íåñðàáàòûâàíèé r. Íàïðèìåð, ïðè n=50 èñïûòàíèé çàôèêñè-

ðîâàíî r=4 îòêàçîâ. Íà ãðàôèêå êîíòðîëÿ ýòà òî÷êà ïîïàäàåò â îáëàñòü íåîïðåäåëåííî-

ñòè (ðèñ.9.8), òàê ÷òî ÷èñëî èñïûòàíèé íåîáõîäèìî óâåëè÷èòü. Èñïûòàíèÿ ïðåêðàùà-

þòñÿ, êîãäà òî÷êà ïîïàäàåò â îáëàñòü ïðèåìêè H

èëè áðàêîâêè H

. Èç ãðàôèêà êîí-

òðîëÿ è óðàâíåíèÿ A(n), ñëåäóåò, ÷òî ìèíèìàëüíîå ÷èñëî ïðîá, íåîáõîäèìîå äëÿ âû-

ïîëíåíèÿ óñëîâèÿ ïðèåìêè, ñîñòàâëÿåò n

=77.

9.2.3. Последовательный контроль средней наработки

Ïðè ïëàíèðîâàíèè êîíòðîëÿ ñðåäíåé íàðàáîòêè â îáùåì ñëó÷àå íåîá-

õîäèìî ðàñïîëàãàòü ïîëíîé âûáîðî÷íîé ñîâîêóïíîñòüþ {T

} ñëó÷àéíûõ íà-

ðàáîòîê îáúåìà n. Ïî çíà÷åíèÿì {T

} âû÷èñëÿåòñÿ ñóììàðíàÿ íàðàáîòêà

, íà êîòîðóþ ïðè ïëàíèðîâàíèè óñòàíàâëèâàþòñÿ êðèòè÷åñêèé ïðèåìî÷-

íûé è áðàêîâî÷íûé óðîâíè, ÿâëÿþùèåñÿ ôóíêöèåé îáúåìà èñïûòàíèé n.

Ãðàôè÷åñêîå èçîáðàæåíèå ëèíèé ïðèåìêè è áðàêîâêè â êîîðäèíàòàõ (r,T

)

èëè (r,T

) óïðîùàåò ïðèíÿòèå ðåøåíèÿ ïî èñïûòàíèÿì [3].

Ãèïîòåçû ïðè êîíòðîëå ñðåäíåé íàðàáîòêè çàïèñûâàþòñÿ â âèäå

: T

³ T

, H

: T

£ T

, (9.74)

ãäå T

è T

- êîíòðîëèðóåìûå óðîâíè ãåíåðàëüíîé ñðåäíåé íàðàáîòêè T

Äëÿ óïðîùåíèÿ ïðîöåäóðû

àíàëîãè÷íî îäíîñòóïåí÷àòîìó

ìåòîäó ïðèåìêó èëè áðàêîâêó

ïðèíÿòî ïðîâîäèòü íå ïî óðîâíþ

ñàìîãî êîíòðîëèðóåìîãî ïîêàçà-

òåëÿ (íàðàáîòêè), à ïî ñâÿçàí-

íîìó ñ íèì ÷èñëó âîçíèêøèõ

îòêàçîâ r çà çàäàííóþ ñóììàð-

íóþ íàðàáîòêó èçäåëèé T

[5].

Ïðè ýòîì ÷èñëî èçäåëèé ìîæåò

áûòü ëþáûì è ïëàíèðîâàíèå çà-

êëþ÷àåòñÿ â ïîñòðîåíèè ëèíèé

ïðèåìêè è áðàêîâêè â êîîðäèíà-

òàõ (r,T

) èëè (r,T

A(n)

B(n)

0 50 100

Ðèñ.9.8. Ãðàôèê äëÿ êîíòðîëÿ âåðîÿòíîñòè

ïðè ðàñïðåäåëåíèè Ïóàññîíà (ê ïðèìåðó 9.14)

189

Ïðè ýêñïîíåíöèàëüíîì ðàñïðåäåëåíèè âûáîðî÷íûõ íàðàáîòîê óñëîâíàÿ

ïëîòíîñòü âåðîÿòíîñòè îïèñûâàåòñÿ ôóíêöèåé ñ åäèíñòâåííûì íåèçâåñò-

íûì ïàðàìåòðîì l=1/Ò

, â îòíîøåíèè êîòîðîãî è ìîãóò ïðîâåðÿòüñÿ ãè-

ïîòåçû (9.74). Îòíîøåíèå ïðàâäîïîäîáèÿ (9.53) ïðèâîäèòñÿ ê âèäó [11]

T T

T T T

- -

1 1

1 1 0

exp( /)

exp( / )

exp

. (9.75)

Ïîñëå ëîãàðèôìèðîâàíèÿ è ïðîñòûõ ïðåîáðàçîâàíèé èç âûðàæåíèÿ

(9.75) ìîæíî ïîëó÷èòü óñëîâèÿ ïðèåìêè (ïðèíÿòèÿ ãèïîòåçû H

), áðàêîâ-

êè (ïðèíÿòèÿ ãèïîòåçû H

) è íåîïðåäåëåííîñòè, ñîîòâåòñòâåííî:

( ) ( )

T T

An T

T T

S S

= £

ln ln

/ /

()

ln ln

/ /

(

)

1 1

1 0

, , (9.76)

B(n) < T

< A(n). (9.77)

Ïðè ðàâåíñòâàõ â âûðàæåíèÿõ (9.76) ìîæíî ïîëó÷èòü óðàâíåíèÿ ëèíèé

ïðèåìêè A(n) è áðàêîâêè B(n) â êîîðäèíàòàõ (n,T

), êîòîðûå áóäóò ðàç-

äåëÿòü îáëàñòè ïðèåìêè, áðàêîâêè è íåîïðåäåëåííîñòè (ïðîäîëæåíèÿ èñ-

ïûòàíèé).

Ïðàêòè÷åñêè èñïîëüçîâàíèå ãðàôèêîâ êîíòðîëÿ â êîîðäèíàòàõ (n,T

) íå

î÷åíü óäîáíî, òàê êàê äëÿ åãî ïîñòðîåíèÿ òðåáóåòñÿ ïðîâåäåíèå èñïûòàíèé

âñåé âûáîðêè n. ×àùå èñïîëüçóþòñÿ ãðàôèêè â êîîðäèíàòàõ, ñâÿçàííûõ ñ

òåêóùèì êîëè÷åñòâîì îòêàçîâ r â âûáîðêå. Êðîìå òîãî, ïðè èñïîëüçîâàíèè

êîîðäèíàò (r,T

) ïîëîæåíèå ãðàíèö îáëàñòåé ïðèåìêè è áðàêîâêè íå çà-

âèñèò îò àáñîëþòíûõ çíà÷åíèé T

è T

, à ïîëíîñòüþ îïðåäåëÿåòñÿ èõ îòíî-

øåíèåì T

è çíà÷åíèÿìè ðèñêîâ a è b. Â ýòîì ñëó÷àå èç îòíîøåíèé

(9.76) ìîæíî ïîëó÷èòü óðàâíåíèÿ ëèíèé ïðèåìêè è áðàêîâêè â âèäå [4,5]

r = a(T

- T

), r = aT

+ r

, (9.78)

ãäå ÷èñëåííûå çíà÷åíèÿ êîýôôèöèåíòîâ a, r

è îòíîøåíèÿ T

ìîæíî

îïðåäåëèòü ïî òàáëèöàì (ñì.ïðèë.XI, òàáë.XI.5) [4,5] èëè ðàññ÷èòàòü ïî

ôîðìóëàì:

1ln

(9.79)

Ïðè íàëè÷èè îòêàçîâ ãðàôèêîì èñïûòàíèé ÿâëÿåòñÿ ñòóïåí÷àòàÿ ëè-

íèÿ, ñóììà îòðåçêîâ êîòîðîé, ïàðàëëåëüíûõ îñè T

, ðàâíà îòíîøåíèþ

ñóììàðíîé íàðàáîòêè èçäåëèé â ìîìåíò âðåìåíè t ê çíà÷åíèþ T

, à ñóììà

îòðåçêîâ, ïàðàëëåëüíûõ îñè r, ðàâíà ÷èñëó îòêàçîâ èçäåëèé ê ìîìåíòó t.

Ïðè îòñóòñòâèè îòêàçîâ ãðàôèê èñïûòàíèé ñîâïàäàåò ñ îñüþ T

, ïðè

ýòîì ñóììàðíàÿ íàðàáîòêà îáðàçöîâ T

=nt.

190

Ïðè èñïûòàíèÿõ áåç âîññòàíîâëåíèÿ èëè çàìåíû ñóììàðíàÿ íàðàáîòêà

â ìîìåíò âðåìåíè t âû÷èñëÿåòñÿ ïî ôîðìóëå

( )

T n rt T

= - +

. (9.80)

Ïðè èñïûòàíèÿõ ñ âîññòàíîâëåíèåì èëè çàìåíîé ñóììàðíàÿ íàðàáîòêà

â ìîìåíò âðåìåíè t âû÷èñëÿåòñÿ ïî ôîðìóëå

T nt t

âi

= -

, (9.81)

ãäå t

âi

- äëèòåëüíîñòü âîññòàíîâëåíèÿ èëè çàìåíû i-ãî èç r îòêàçàâøèõ èçäåëèé.

Ïî ôîðìóëàì (9.79) ìîæíî âèäåòü, ÷òî åñëè ðèñêè èçãîòîâèòåëÿ è çà-

êàç÷èêà ñîâïàäàþò (a=b), òî r

=aT

è óðàâíåíèÿ ïðÿìûõ (9.78) èìå-

þò âèä r

=aT

±r

Íèæíþþ îöåíêó ñðåäíåé ïðîäîëæèòåëüíîñòè êîíòðîëÿ äëÿ âîññòàíàâ-

ëèâàåìûõ èçäåëèé ïðè T=T

ìîæíî ðàññ÷èòàòü ïî ôîðìóëå [4,5]:

( )

1 1

- -

ln ln

(9.82)

Çíà÷åíèÿ (T

)

ñð

òàêæå ïðèâåäåíû â ïðèë.XI (òàáë.XI.5).

Ïðèìåð 9.15 [4]. Ïî äàííûì ïðèìåðà 9.6 îïðåäåëèòü ïëàí êîíòðîëÿ ïîñëåäîâà-

òåëüíûì ìåòîäîì.

Ïî òàáë.XI.5 (ïðèë.XI) èëè ôîðìóëàì (9.79) äëÿ a=b=0,2, T

=1,765 íàõîäèì

çíà÷åíèÿ âåëè÷èí:

a r

= =

17651

1765

1346

102

1765

244

102

17651

181

ln,

, ,

ln,

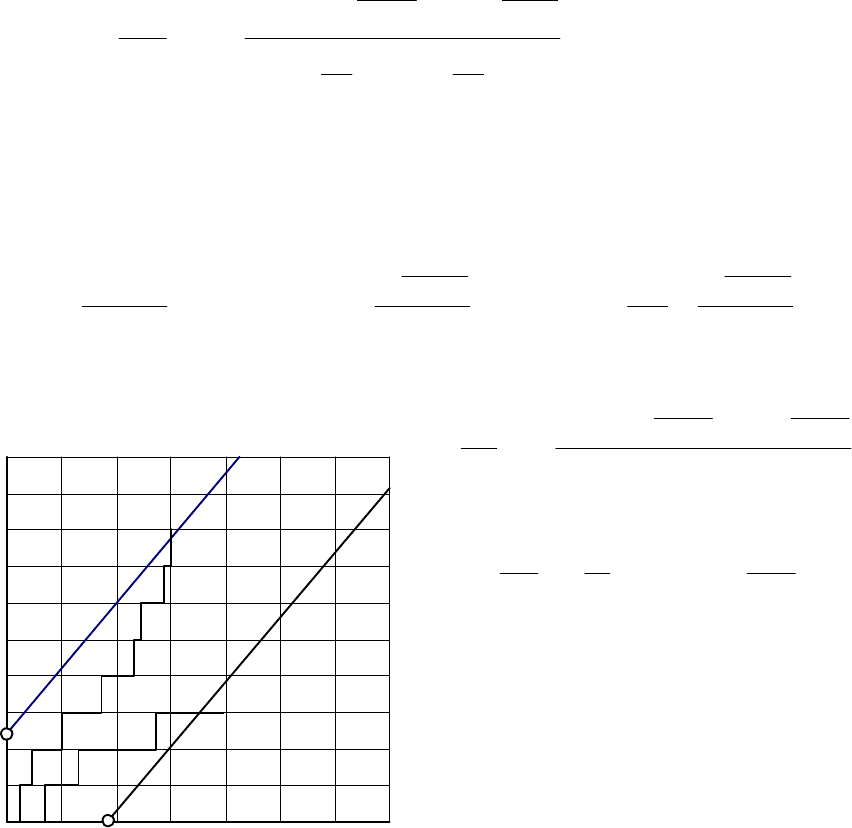
Ïî ðàññ÷èòàííûì äàííûì ñòðîèòñÿ ãðàôèê ïîñëåäîâàòåëüíîãî êîíòðîëÿ (ðèñ.9.9).

Íèæíÿÿ îöåíêà ñðåäíåé ïðîäîëæèòåëüíîñòè êîíòðîëÿ ïî ôîðìóëå (9.82):

( )

102

17651 1765

423

,ln

, ln,

Îðèåíòèðîâî÷íûé îáúåì âûáîðêè ïî

ôîðìóëå (9.30)

= × +

1 423

3000

600

1 2538

, ,.

Îêîí÷àòåëüíî ìîæíî ïðèíÿòü n=25.

Ïðè êîíòðîëå íåîáõîäèìî îðãàíèçîâàòü

25 öèêëîâ ðàáîòû (äëÿ âîññòàíàâëèâàåìûõ

èçäåëèé) èëè èñïûòàíèÿ 25 èçäåëèé (äëÿ íå-

âîññòàíàâëèâàåìûõ èçäåëèé). Â ïðîöåññå êîí-

òðîëÿ îïðåäåëÿåòñÿ ñóììàðíàÿ íàðàáîòêà èç-

äåëèé T

ê ìîìåíòó î÷åðåäíîãî îòêàçà r, íà

ãðàôèêå (ðèñ.9.9) íàíîñÿòñÿ òî÷êè ñ êîîðäè-

íàòàìè (T

,r), ïî êîòîðûì ñòðîèòñÿ ñòó-

ïåí÷àòàÿ ëèíèÿ èñïûòàíèé. Èñïûòàíèÿ ïðî-

äîëæàþòñÿ äî òåõ ïîð, ïîêà ëèíèÿ èñïûòàíèé

ïðîõîäèò â îáëàñòè íåîïðåäåëåííîñòè, îãðà-

íè÷åííîé ëèíèÿìè ïðèåìêè 1 è áðàêîâêè 2.

0 4

Ðèñ.9.9. Ãðàíèöû îáëàñòåé ïðèåìêè (H

)

è áðàêîâêè (

) (ê ïðèìåðó 9.15)