Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1
Подождите немного. Документ загружается.


71
îïèñàíèÿ ñîñòîÿíèÿ ñèñòåì ýëåìåíòîâ è îïðåäåëåíèÿ íåêîòîðûõ ïàðàìåò-
ðîâ íàäåæíîñòè ìîæíî èñïîëüçîâàòü íåêîòîðûå ìåòîäû ìàòåìàòè÷åñêîé
ëîãèêè, â ÷àñòíîñòè àëãåáðû ëîãèêè.
2.6.1. Основные понятия алгебры логики [24-26]
Ëîãè÷åñêîé ïåðåìåííîé (âûñêàçûâàíèåì) íàçûâàåòñÿ âûðàæåíèå, êî-
òîðîå ìîæåò ïðèíèìàòü èñòèííîñòíîå çíà÷åíèå "È" (èñòèíà) èëè "Ë"
(ëîæü). Âìåñòî ýòèõ ñèìâîëîâ ÷àñòî óïîòðåáëÿþòñÿ ÷èñëà 1 è 0 ñîîòâåò-
ñòâåííî (îáû÷íî 1 îçíà÷àåò, ÷òî ñîáûòèå ïðîèçîøëî, 0 - íå ïðîèçîøëî).
Ëîãè÷åñêîé îïåðàöèåé íàçûâàåòñÿ ïîñòðîåíèå íîâûõ ëîãè÷åñêèõ ïåðå-
ìåííûõ (âûñêàçûâàíèé) ñ ïîìîùüþ ÷àñòèöû "íå", ñîþçîâ "è", "èëè", "åñëè
..., òî ..." è ò.ä. Çíàêè ëîãè÷åñêèõ îïåðàöèé íàçûâàþòñÿ ëîãè÷åñêèìè
ñâÿçêàìè.  ìàòåìàòè÷åñêîé ëîãèêå è àëãåáðå ëîãèêè (àëãåáðå âûñêàçûâà-
íèé, áóëåâîé àëãåáðå) èñïîëüçóþòñÿ ëîãè÷åñêèå îïåðàöèè îòðèöàíèÿ (îáî-
çíà÷åíèå`A), ëîãè÷åñêîãî ñëîæåíèÿ (A
1
ÚA
2
èëè A
1
+A
2
), ëîãè÷åñêîãî óì-
íîæåíèÿ (A
1
ÙA
2
èëè A
1
×A
2
), àíàëîãè÷íûå ñîîòâåòñòâóþùèì îïåðàöèÿì â
òåîðèè âåðîÿòíîñòåé, à òàêæå íåêîòîðûå äîïîëíèòåëüíûå ëîãè÷åñêèå îïå-
ðàöèè.  òàáë.2.2 ïðèâåäåíû îñíîâíûå äâóõìåñòíûå ëîãè÷åñêèå îïåðàöèè
è ëîãè÷åñêèå ñâÿçêè, à òàêæå çíà÷åíèÿ ëîãè÷åñêèõ ïåðåìåííûõ, îáðàçî-
âàííûõ ýòèìè ëîãè÷åñêèìè îïåðàöèÿìè, ïðè âñåõ âîçìîæíûõ ñî÷åòàíèÿõ
çíà÷åíèé ïåðåìåííûõ A
1
è A
2
.
Äëÿ îñíîâíûõ ëîãè÷åñêèõ îïåðàöèé ñëîæåíèÿ è óìíîæåíèÿ ñïðàâåäëè-
âû ñëåäóþùèå îñíîâíûå çàêîíû ëîãèêè:
- çàêîíû àññîöèàòèâíîñòè:
A + (B+C) º (A+B) + C º A + B + C, A(BC) º (AB)C º ABC; (2.249)
- çàêîíû êîììóòàòèâíîñòè:
A + B º B + A, AB º BA; (2.250)
- çàêîíû äèñòðèáóòèâíîñòè:
A(B+C) º (AB) + (AC), A + (BC) º (A+B)(A+C); (2.251)
- çàêîíû èíâåðñèé (ïðàâèëà äå Ìîðãàíà):
A B AB AB A B+ º º +, ; (2.252)
- çàêîíû èäåìïîòåíòíîñòè:
A + A º A, AA º A; (2.253)
- çàêîíû ïîãëîùåíèÿ:
A(A+B) º A, A + (AB) º A; (2.254)
- çàêîíû ñêëåèâàíèÿ:
(A + B)(`A + B) º B; (AB)(`AB) º B; (2.255)
- çàêîí èñêëþ÷åííîãî òðåòüåãî:
A +`A º 1; (2.256)
- çàêîí ïðîòèâîðå÷èÿ:
A`A º 0. (2.257)
Êðîìå òîãî, äîñòàòî÷íî î÷åâèäíû ñëåäóþùèå ñîîòíîøåíèÿ:
A + 1 º 1, A + 0 º A, A×1 º A, A×0 º 0. (2.258)
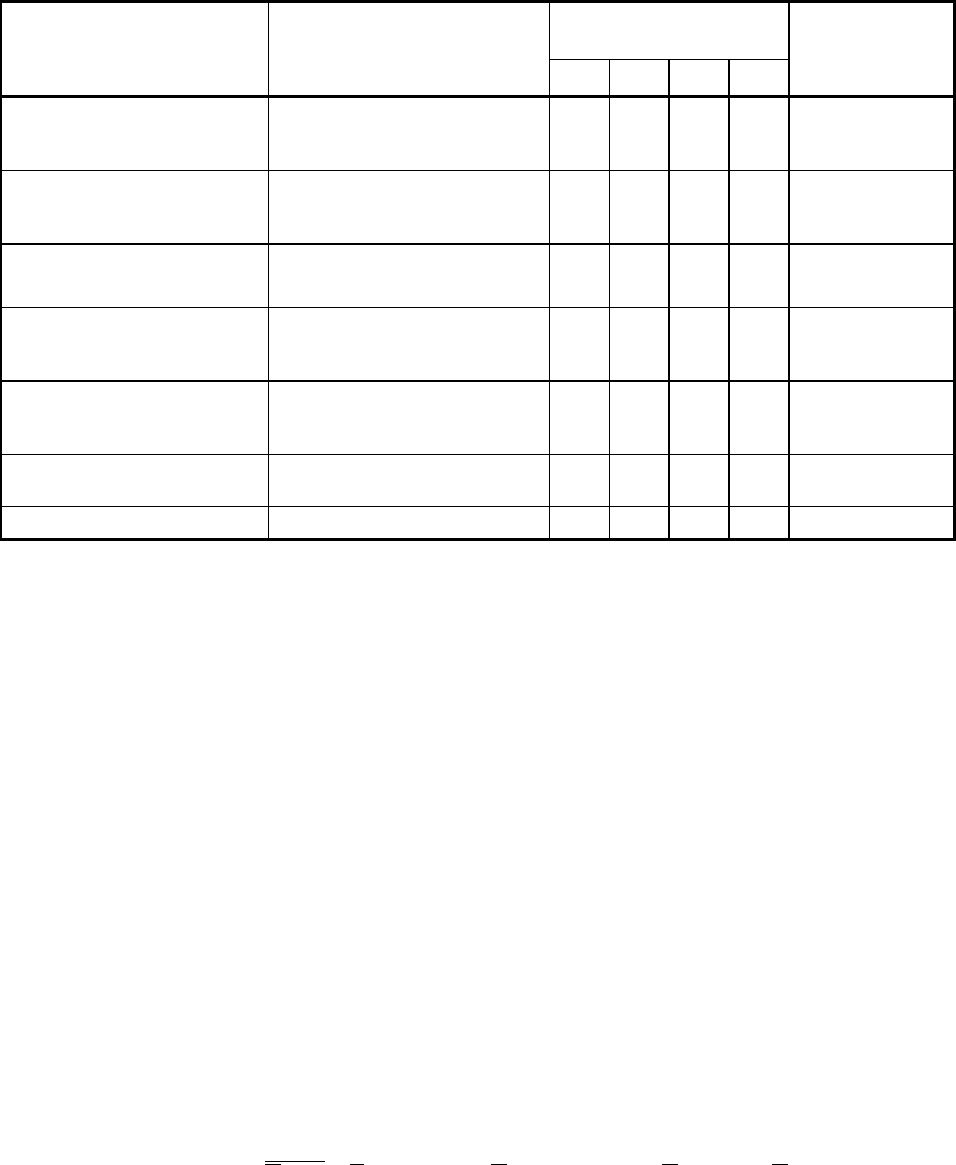
72
Ôîðìóëà àëãåáðû ëîãèêè (ÔÀË) - âûðàæåíèå, ñîñòàâëåííîå èç ëîãè-
÷åñêèõ ïåðåìåííûõ ñ ïîìîùüþ ëîãè÷åñêèõ ñâÿçîê. Ôóíêöèÿ, âûðàæåííàÿ ñ
ïîìîùüþ ôîðìóëû àëãåáðû ëîãèêè, íàçûâàåòñÿ ôóíêöèåé àëãåáðû ëîãèêè.
Òàê êàê âñå ïåðåìåííûå, âõîäÿùèå â ÔÀË, - ëîãè÷åñêèå è ðåçóëüòàò ëþ-
áîé ëîãè÷åñêîé îïåðàöèè - òàêæå ëîãè÷åñêàÿ ïåðåìåííàÿ, òî è ÔÀË - ëî-
ãè÷åñêàÿ ïåðåìåííàÿ è ìîæåò ïðèíèìàòü òîëüêî äâà çíà÷åíèÿ - 1 èëè 0.
Äëÿ îïðåäåëåíèÿ ïîñëåäîâàòåëüíîñòè îïåðàöèé â ÔÀË èñïîëüçóþòñÿ
ñêîáêè. Ñ÷èòàåòñÿ, ÷òî â îòñóòñòâèå ñêîáîê ïðèîðèòåò ïðèìåíåíèÿ ñâÿçîê
â ôîðìóëàõ ñëåäóþùèé (â ïîðÿäêå óáûâàíèÿ):` , Ù(×), Ú(+), ®, «.
Ôîðìóëà àëãåáðû ëîãèêè ìîæåò áûòü ïðåîáðàçîâàíà è óïðîùåíà ñ ïî-
ìîùüþ îñíîâíûõ çàêîíîâ ëîãèêè (2.249)-(2.258). Êðîìå òîãî, â àëãåáðå ëî-
ãèêè äîêàçûâàåòñÿ, ÷òî âñå ëîãè÷åñêèå îïåðàöèè ìîãóò áûòü âûðàæåíû ÷å-
ðåç îïåðàöèè ëîãè÷åñêîãî ñëîæåíèÿ (äèçúþíêöèè) Ú (èëè +), ëîãè÷åñêîãî
óìíîæåíèÿ (êîíúþíêöèè) Ù (èëè ×) è ëîãè÷åñêîãî îòðèöàíèÿ` .
Íàïðèìåð:
A ® B º
`
A + B, (A « B) º (
`
A + B)(A +
`
B). (2.259)
Òàêèì îáðàçîì, ëþáóþ ôîðìóëó ìîæíî ïðèâåñòè ê âèäó, ñîäåðæàùåìó òîëüêî îïå-
ðàöèè ëîãè÷åñêîãî ñëîæåíèÿ, óìíîæåíèÿ è îòðèöàíèÿ. Òàêàÿ ôîðìà ÔÀË íàçûâàåòñÿ
íîðìàëüíîé ôîðìîé. Íàïðèìåð:
(
)
(
)
A BC A ABC A ABC AB+ × ® º × × + º × × + ×
. (2.260)
2.6.2. Таблицы истинности формул алгебры логики [26]
Ïîëüçóÿñü îïðåäåëåíèÿìè ëîãè÷åñêèõ îïåðàöèé, ìîæíî íàéòè çíà÷åíèå
ÔÀË ïðè äàííîì íàáîðå çíà÷åíèé ïåðåìåííûõ. Óäîáíîé ôîðìîé çàïèñè
ïðè íàõîæäåíèè çíà÷åíèé ôîðìóëû, ñîîòâåòñòâóþùèõ âñåì âîçìîæíûì
íàáîðàì çíà÷åíèé ïåðåìåííûõ, ÿâëÿåòñÿ òàáëèöà èñòèííîñòè.
Òàáëèöà 2.2
ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ [8]
Îáîçíà÷åíèå
ëîãè÷åñêîé
Íàçâàíèå
ëîãè÷åñêîé îïåðàöèè
Çíà÷åíèå
ïðè A
1
è A
2
Íàèìåíîâàíèå
ëîãè÷åñêîé
îïåðàöèè èëè ñâÿçêè
èëè ñâÿçêè
00
01
10
11
îïåðàöèè
A
1
ÚA
2
èëè A
1
+A
2
äèçúþíêöèÿ,
ëîãè÷åñêîå ñëîæåíèå,
ëîãè÷åñêîå "èëè"
0 1 1 1
A
1
èëè A
2
A
1
ÙA
2
èëè A
1
×A
2
èëè A
1
&A
2
êîíúþíêöèÿ,
ëîãè÷åñêîå óìíîæåíèå,
ëîãè÷åñêîå "È"
0 0 0 1
A
1
è A
2
A
1
®A
2
èëè A
1
ÞA
2
èëè A
1
ÊA
2
èìïëèêàöèÿ,
ëîãè÷åñêîå ñëåäîâàíèå
1 1 0 1
åñëè A
1
, òî A
2
A
1
ÅA
2
èëè A
1
DA
2
ðàçäåëèòåëüíàÿ
äèçúþíêöèÿ,
ðàçäåëèòåëüíîå "ÈËÈ"
0 1 1 0
ëèáî A
1
,
ëèáî A
2
A
1
ºA
2
èëè A
1
«A
2
èëè A
1
ÛA
2
ýêâèâàëåíöèÿ,
ýêâèâàëåíòíîñòü,
òîæäåñòâåííîñòü
1 0 0 1
A
1
ýêâèâà-
ëåíòíî A
2
A
1
/A
2
àíòèêîíúþíêöèÿ
1 1 1 0
íåâåðíî, ÷òî
A
1
è A
2
A
1
O
A
2
èëè A
1
`ÚA
2
àíòèäèçúþíêöèÿ
1 0 0 0
íè A
1
,
íè A
2
73
 ïåðâûõ ñòîëáöàõ òàá-
ëèöû (òàáë.2.3) ïåðå÷èñëÿþò-
ñÿ âñå âîçìîæíûå ñî÷åòàíèÿ
çíà÷åíèé ëîãè÷åñêèõ ïåðå-
ìåííûõ, âõîäÿùèõ â ôîðìóëó.
Òàê êàê êàæäàÿ èç íèõ ìîæåò
ïðèíèìàòü äâà çíà÷åíèÿ (1 è
0), òî ïðè ÷èñëå ïåðåìåííûõ
n îáùåå êîëè÷åñòâî òàêèõ ñî-
÷åòàíèé ðàâíî 2
n
, ò.å. òàáëèöà
äîëæíà ñîäåðæàòü 2
n
ñòðîê.
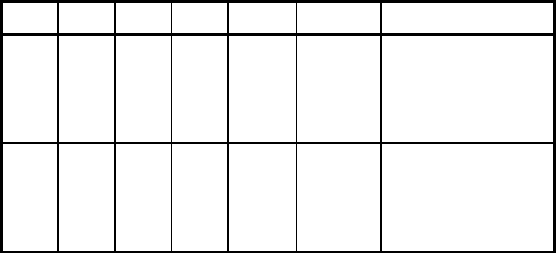
Äëÿ óäîáñòâà ñðàâíåíèÿ òàáëèö ïðèíÿò ñëåäóþùèé ïîðÿäîê çàïîëíåíèÿ
ïåðâûõ ñòîëáöîâ: ïåðåìåííûå ðàñïîëàãàþòñÿ â àëôàâèòíîì ïîðÿäêå èëè â
ïîðÿäêå óâåëè÷åíèÿ çíà÷åíèé èíäåêñîâ; âåðõíÿÿ ïîëîâèíà ïåðâîãî ñòîëáöà
çàïîëíÿåòñÿ çíà÷åíèÿìè 1, íèæíÿÿ - 0; âî âòîðîì ñòîëáöå ÷åðåäîâàíèå
çíàêîâ 1 è 0 ïðîèçâîäèòñÿ ÷åðåç ÷åòâåðòü ñòîëáöà, â òðåòüåì - ÷åðåç îäíó
âîñüìóþ è ò.ä., ò.å. ïåðèîä ÷åðåäîâàíèÿ çíà÷åíèé â êàæäîì ñëåäóþùåì
ñòîëáöå âäâîå ìåíüøå, ÷åì â ïðåäûäóùåì, â ñòîëáöå ïîñëåäíåé n-îé ïåðå-
ìåííîé çíà÷åíèÿ 1 è 0 ÷åðåäóþòñÿ ïîñòðî÷íî.  ïîñëåäóþùèõ ñòîëáöàõ
òàáëèöû çàïèñûâàþòñÿ çíà÷åíèÿ îïåðàöèé, âõîäÿùèõ â ôîðìóëó, â ïîðÿä-
êå èõ âûïîëíåíèÿ.  ïîñëåäíèé ñòîëáåö òàáëèöû çàïèñûâàþòñÿ çíà÷åíèÿ
ôîðìóëû â öåëîì. Ñîêðàùåííàÿ òàáëèöà èñòèííîñòè ñîñòîèò òîëüêî èç
ñòîëáöîâ çíà÷åíèé ïåðåìåííûõ è ñòîëáöà çíà÷åíèé ôîðìóëû â öåëîì.
2.6.3. Переключательные схемы [26,27]
Íàãëÿäíîé èëëþñòðàöèåé ôîðìóë àëãåáðû ëîãèêè è èõ èñïîëüçîâàíèÿ
ïðè ðåøåíèè òåõíè÷åñêèõ çàäà÷ ÿâëÿþòñÿ ïåðåêëþ÷àòåëüíûå ñõåìû.
Ïåðåêëþ÷àòåëüíàÿ ñõåìà - óñòðîéñòâî èç ïåðåêëþ÷àòåëåé (êîíòàêòîâ)
è ïðîâîäíèêîâ, ñâÿçûâàþùèõ äâà ïîëþñà - âõîä è âûõîä, èëè èñòî÷íèêà è
ïîòðåáèòåëÿ. Êàæäûé ïåðåêëþ÷àòåëü ìîæåò íàõîäèòüñÿ â äâóõ ñîñòîÿíèÿõ
- çàìêíóòîì è ðàçîìêíóòîì, ÷òî ñîîòâåòñòâóåò çíà÷åíèÿì ëîãè÷åñêèõ ïå-
ðåìåííûõ, îïðåäåëÿþùèõ ñîñòîÿíèå ïåðåêëþ÷àòåëåé, 1 è 0. Ñîñòîÿíèå
âñåé ñõåìû (çàìêíóòîå èëè ðàçîìêíóòîå, ò.å. òàêæå 1 èëè 0) îïðåäåëÿåòñÿ
ñòðóêòóðîé ñõåìû è ñî÷åòàíèåì ñîñòîÿíèé ïåðåêëþ÷àòåëåé. Ïåðåêëþ÷à-
òåëüíûå ñõåìû - àíàëîãè ñòðóêòóðíî-ëîãè÷åñêèõ ñõåì íàäåæíîñòè
(ñì.ãë.5).
Íà ðèñ.2.11 ïðåäñòàâëåíû äâà âîçìîæíûõ âàðèàíòà ñîåäèíåíèÿ äâóõ ïåðåêëþ÷àòå-
ëåé - ïîñëåäîâàòåëüíîå è ïàðàëëåëüíîå. Ïåðâîìó ñîîòâåòñòâóåò ôîðìóëà êîíúþíêöèè
(óìíîæåíèÿ) ÀÂ, âòîðîìó - ôîðìóëà äèçúþíêöèè (ñëîæåíèÿ) À+Â.
Ìàíèïóëèðóÿ ïîñëåäîâàòåëüíûìè è ïàðàëëåëüíûìè ñîåäèíåíèÿìè,
ìîæíî ñîñòàâèòü ñõåìó, ñîîòâåòñòâóþùóþ ëþáîé ÔÀË, ïðè÷åì äëÿ ýòîãî
ìîæíî èñïîëüçîâàòü íå òîëüêî íåçàâèñèìûå ïåðåêëþ÷àòåëè, íî è ïåðå-
êëþ÷àòåëè, ñîñòîÿíèå êîòîðûõ çàâèñèò îò ñîñòîÿíèÿ äðóãèõ ïåðåêëþ÷àòå-
ëåé. Ïåðåêëþ÷àòåëè, êîòîðûå çàìûêàþòñÿ è ðàçìûêàþòñÿ îäíîâðåìåííî,
íàçûâàþòñÿ èäåíòè÷íûìè, à êîòîðûå ðàçìûêàþòñÿ, êîãäà äðóãèå çàìûêà-
þòñÿ, è íàîáîðîò,- èíâåðñíûìè. Èäåíòè÷íûå ïåðåêëþ÷àòåëè íà ñõåìàõ
îáîçíà÷àþòñÿ îäèíàêîâûìè ñèìâîëàìè, èíâåðñíûå - òåìè æå ñèìâîëàìè ñ
ãîðèçîíòàëüíîé ÷åðòîé (àíàëîãè÷íî îáîçíà÷åíèþ îïåðàöèè îòðèöàíèÿ).
Òàáëèöà 2.3.
ТАБЛИЦА ИСТИННОСТИ ФОРМУЛЫ
(A`B)«(C®A)
A
B
C
`B
A`B
C®A
(A`B)«(C®A)
1 1 1 0 0 1 0
1 1 0 0 0 1 0
1 0 1 1 1 1 1
1 0 0 1 1 1 1
0 1 1 0 0 0 1
0 1 0 0 0 1 0
0 0 1 1 0 0 1
0 0 0 1 0 1 0

74
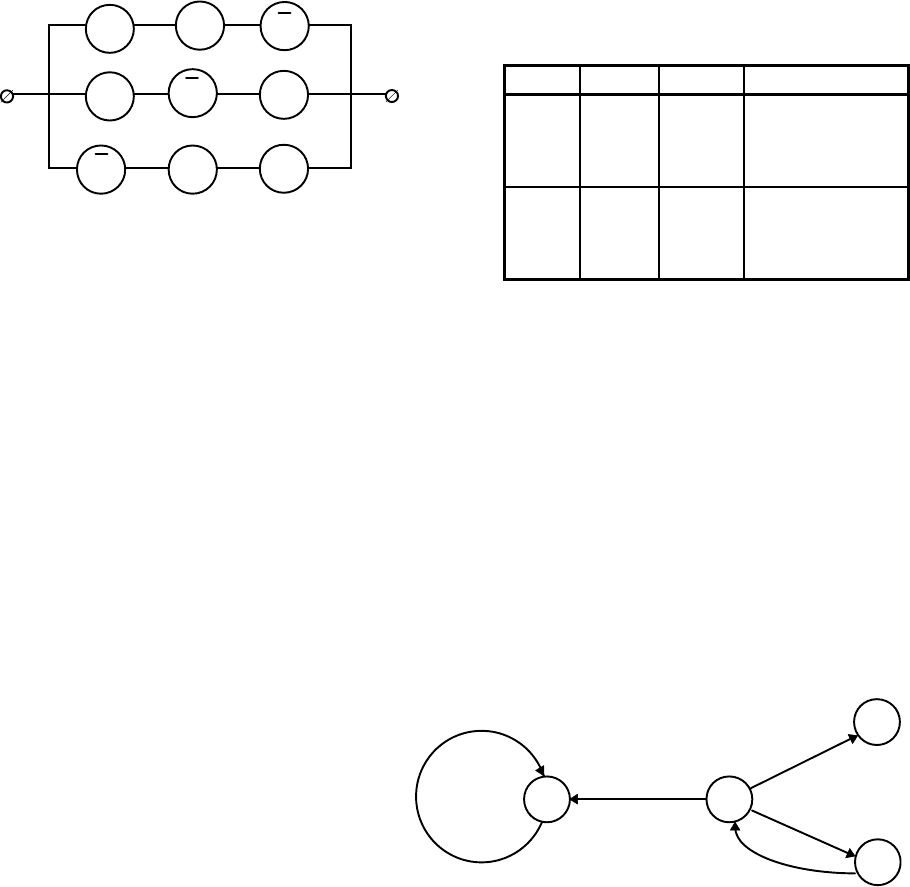
Íà ðèñ.2.12 ïðèâåäåíà ñõåìà, ñîîòâåòñòâóþùàÿ ôîðìóëå A×(C+`B)+B×(C+`A), ñî-
äåðæàùàÿ èäåíòè÷íûå (Ñ) è èíâåðñíûå (À è`A,  è`B) ïåðåêëþ÷àòåëè.
Äëÿ ïåðåêëþ÷àòåëüíûõ ñõåì ìîæíî ñîñòàâëÿòü òàáëèöû èñòèííîñòè, ñ
íèìè ìîæíî ïðîèçâîäèòü òîæäåñòâåííûå ïðåîáðàçîâàíèÿ è óïðîùåíèÿ,
àíàëîãè÷íî òîìó, êàê ýòî äåëàåòñÿ ñ ñàìèìè ôîðìóëàìè àëãåáðû ëîãèêè.
Òîæäåñòâåííûå ïðåîáðàçîâàíèÿ ÔÀË îäíîâðåìåííî îçíà÷àþò è ïðåîáðà-
çîâàíèÿ ñîîòâåòñòâóþùåé åé ïåðåêëþ÷àòåëüíîé ñõåìû. Èíîãäà ñ ïîìîùüþ
òîæäåñòâåííûõ ïðåîáðàçîâàíèé ìîæíî ñóùåñòâåííî óïðîñòèòü èñõîäíóþ
ïåðåêëþ÷àòåëüíóþ ñõåìó áåç èçìåíåíèÿ åå ñâîéñòâ è òàáëèöû èñòèííîñòè.
Íà ðèñ.2.13à ïðåäñòàâëåíà ñõåìà, ñîîòâåòñòâóþùàÿ ôîðìóëå A(D+CE)+B(E+CD),
íà ðèñ.2.13á - ñõåìà ïî ôîðìóëå AD+ACE+BE+BCD. Ñõåìû îáëàäàþò îäèíàêîâûìè
ñâîéñòâàìè, íî èñõîäíàÿ ñîäåðæèò âîñåìü ïåðåêëþ÷àòåëåé, à ïðåîáðàçîâàííàÿ - ïÿòü.
 àëãåáðå ëîãèêè äîêàçûâàåòñÿ, ÷òî ëþáóþ ïåðåêëþ÷àòåëüíóþ ñõåìó,
ñîîòâåòñòâóþùóþ ôîðìóëå ñ n ïåðåìåííûìè, ìîæíî óïðîñòèòü äî âàðèàí-
òà, ñîäåðæàùåãî íå áîëåå 2
n
/n ïåðåêëþ÷àòåëåé.
Íàðÿäó ñ àíàëèçîì ïåðåêëþ÷àòåëüíûõ ñõåì âîçìîæåí è ñèíòåç ñõåìû ñ
çàäàííûìè ñâîéñòâàìè íà îñíîâàíèè ÔÀË èëè òàáëèöû èñòèííîñòè.
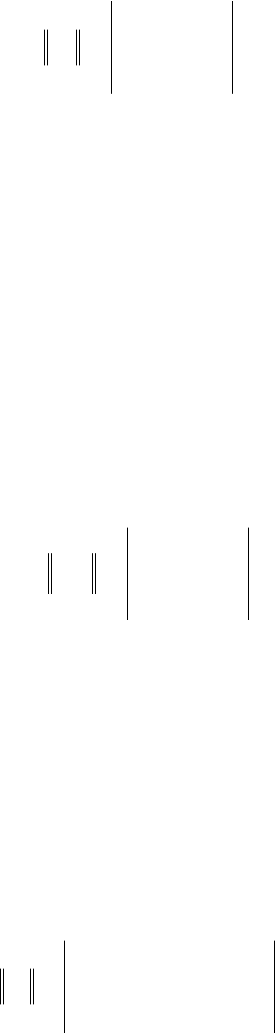
Íà ðèñ.2.14 ïðèâåäåíà ïåðåêëþ÷àòåëüíàÿ ñõåìà ïî ôîðìóëå ãîëîñîâàíèÿ "2 èç 3"
F º A
×
B
×`
C + A
×`
B
×
C + A
×
B
×`
C, (2.261)
åå òàáëèöà èñòèííîñòè ïðèâåäåíà â òàáë.2.4.
Îñíîâíûå îïåðàöèè è ôîðìóëû àëãåáðû ëîãèêè, òîæäåñòâåííûå ïðåîá-
ðàçîâàíèÿ ôîðìóë è ïåðåêëþ÷àòåëüíûõ ñõåì â òåîðèè íàäåæíîñòè èñïîëü-
çóþòñÿ ïðè àíàëèçå íàäåæíîñòè ñëîæíûõ òåõíè÷åñêèõ ñèñòåì (ñì.ãë.5).
A
B
A
B
à)
á)
B
С
B
С
А
A
Ðèñ.2.11.Ïîñëåäîâàòåëüíîå (à) è ïàðàëëåëüíîå Ðèñ.2.12. Ïåðåêëþ÷àòåëüíàÿ ñõåìà
(á) ñîåäèíåíèå ïåðåêëþ÷àòåëåé ñ èäåíòè÷íûìè è èíâåðñíûìè
ïåðåêëþ÷àòåëÿìè
B
С
D
E
C
A
E
D
B
A
E
D
C
à) á)
Ðèñ.2.13. Èñõîäíàÿ (à) è ïðåîáðàçîâàííàÿ (á) ïåðåêëþ÷àòåëüíûå ñõåìû
75
2.7. Элементы теории графов
Íåêîòîðûå ïðàêòè÷åñêèå è òåîðåòè÷åñêèå çàäà÷è íàäåæíîñòè ìîæíî
ñâåñòè ê ðàññìîòðåíèþ ñîâîêóïíîñòè âîçìîæíûõ ñîñòîÿíèé îáúåêòîâ è
ïåðåõîäîâ èç îäíîãî ñîñòîÿíèÿ â äðóãîå. Òàêèå çàäà÷è ýôôåêòèâíî ðåøà-
þòñÿ ñ ïðèâëå÷åíèåì ìåòîäîâ òåîðèè ãðàôîâ.
2.7.1. Основные понятия и определения [28,29]
Ãðàôîì íàçûâàåòñÿ ñîâîêóïíîñòü òî÷åê (âåðøèí) è ðåáåð, ñîåäèíÿþ-
ùèõ âñå èëè íåêîòîðûå âåðøèíû ìåæäó ñîáîé (ðèñ.2.15). Âåðøèíû, ñî-
åäèíåííûå ðåáðîì, à òàêæå ðåáðà, èìåþùèå îáùóþ âåðøèíó, íàçûâàþòñÿ
ñìåæíûìè, à ðåáðî è ëþáàÿ èç äâóõ åãî âåðøèí - èíöèäåíòíûìè.
Ðåáðî, äëÿ êîòîðîãî çàäàíî íà-
ïðàâëåíèå, íàçûâàåòñÿ îðèåíòèðî-
âàííûì èëè äóãîé. Ãðàô, ñîäåðæà-
ùèé òîëüêî äóãè, íàçûâàåòñÿ îðè-
åíòèðîâàííûì, ñîäåðæàùèé òîëü-
êî íåîðèåíòèðîâàííûå ðåáðà - íå-
îðèåíòèðîâàííûì. Ðåáðî, íà÷è-
íàþùååñÿ è çàêàí÷èâàþùååñÿ â îäíîé âåðøèíå, íàçûâàåòñÿ ïåòëåé.
Ñìåæíûå âåðøèíû ãðàôà ìîãóò ñîåäèíÿòüñÿ íåñêîëüêèìè ðåáðàìè èëè äó-
ãàìè îäíîãî íàïðàâëåíèÿ. Òàêèå ðåáðà è äóãè íàçûâàþòñÿ êðàòíûìè
(êðàòíîñòü - ÷èñëî êðàòíûõ ðåáåð èëè äóã îäíîãî íàïðàâëåíèÿ).
Íåïðåðûâíàÿ ïîñëåäîâàòåëüíîñòü ðåáåð íàçûâàåòñÿ öåïüþ (â îðèåíòè-
ðîâàííîì ãðàôå - ïóòåì), öåïè èëè ïóòè, â êîòîðûõ íè îäíî ðåáðî èëè äó-
ãà íå âñòðå÷àþòñÿ äâàæäû, - ïðîñòûìè öåïÿìè èëè ïóòÿìè. Çàìêíóòûå
öåïè èëè ïóòè íàçûâàþòñÿ öèêëîì èëè êîíòóðîì.
Ãðàô, â êîòîðîì ìåæäó ëþáûìè äâóìÿ âåðøèíàìè ñóùåñòâóåò öåïü èëè
ïóòü, íàçûâàåòñÿ ñâÿçíûì. Ñâÿçíûé ãðàô, íå èìåþùèé öèêëîâ èëè êîíòó-
ðîâ, íàçûâàåòñÿ äåðåâîì, à åãî íà÷àëüíàÿ âåðøèíà - êîðíåì.
2.7.2. Матричный способ задания графов [28]
Ñóùåñòâóåò íåñêîëüêî ñïîñîáîâ çàäàíèÿ ãðàôîâ. Îäèí èç ñàìûõ ðàñ-
ïðîñòðàíåííûõ è óäîáíûõ - ìàòðè÷íûé.
Òàáëèöà 2.4
ТАБЛИЦА ИСТИННОСТИ ФОРМУЛЫ
F º A B`C + A`B C +`A B C
A B C F
1 1 1 1
1 1 0 1
1 0 1 1
1 0 0 0
0 1 1 1
0 1 0 0
0 0 1 0
0 0 0 0
A
A
B
C
B C
A
B
C
Ðèñ.2.14. Ïåðåêëþ÷àòåëüíàÿ ñõåìà
"ãîëîñîâàíèÿ 2 èç 3"
1
2
3
4
Ðèñ.2.15. Îðèåíòèðîâàííûé ãðàô
76
Ìàòðèöåé ñìåæíîñòè íàçûâàåòñÿ ìàòðèöà, ýëåìåíòû êîòîðîé ðàâíû
êðàòíîñòè ðåáåð èëè äóã, ñîåäèíÿþùèõ âåðøèíû ñ íîìåðàìè, ñîâïàäàþ-
ùèìè ñ íîìåðàìè ñòðîê è ñòîëáöîâ. ×èñëî ñòðîê è ñòîëáöîâ òàêîé ìàòðè-
öû ðàâíî ÷èñëó âåðøèí ãðàôà. Åñëè âåðøèíû ãðàôà íå ñîåäèíåíû äðóã ñ
äðóãîì, òî ñîîòâåòñòâóþùèé ýëåìåíò ìàòðèöû ðàâåí íóëþ.
Íàïðèìåð, ìàòðèöà ñìåæíîñòè ãðàôà íà ðèñ.2.15:
A a
ij
= =
1000
1011
0000
0100
. (2.262)
Äëÿ îðèåíòèðîâàííîãî ãðàôà íîìåð ñòðîêè ýëåìåíòà ñîâïàäàåò ñ íîìå-
ðîì âåðøèíû, èç êîòîðîé äóãà âûõîäèò, à íîìåð ñòîëáöà - ñ íîìåðîì âåð-
øèíû, â êîòîðóþ îíà âõîäèò. Äëÿ íåîðèåíòèðîâàííîãî ãðàôà ìàòðèöà
ñèììåòðè÷íà îòíîñèòåëüíî ãëàâíîé äèàãîíàëè è a
ij
= a
ji
.
Ìàòðèöà ñìåæíîñòè ïîëíîñòüþ îïðåäåëÿåò ñòðóêòóðó ãðàôà. Ñóììà
ýëåìåíòîâ ñòðîêè ìàòðèöû ðàâíà êîëè÷åñòâó äóã, âûõîäÿùèõ èç ñîîòâåòñò-
âóþùåé âåðøèíû, ñóììà ýëåìåíòîâ ñòîëáöîâ - âõîäÿùèõ â íåå.
Åñëè ìàòðèöó ñìåæíîñòè âîçâåñòè â êâàäðàò (ò.å. óìíîæèòü ñàìó íà
ñåáÿ ïî ïðàâèëàì óìíîæåíèÿ ìàòðèö), òî êàæäûé ýëåìåíò ìàòðèöû A
2
a aa
ij
ikkj
k
n
()2
1
=
=
å
(2.263)
è áóäåò ðàâåí ÷èñëó ïóòåé äëèíû 2, èäóùèõ èç âåðøèíû i â âåðøèíó j.
Íàïðèìåð, äëÿ ãðàôà íà ðèñ.2.15 êâàäðàò ìàòðèöû ñìåæíîñòè (2.262):
A a
ij
2
1000
1100
0000
1011
= =
(2)
. (2.264)
Àíàëîãè÷íî ìîæíî ïîëó÷èòü ìàòðèöó, ýëåìåíòû êîòîðîé áóäóò ðàâíû
÷èñëó ïóòåé äëèíû 3, 4 è ò.ä. Ýëåìåíòû a
ij
(m)
ìàòðèöû A
m
ðàâíû ÷èñëó
ïóòåé äëèíû m, èäóùèõ èç âåðøèíû i â âåðøèíó j .
Ìàòðèöåé èíöèäåíòíîñòè íàçûâàåòñÿ ìàòðèöà, ýëåìåíòû êîòîðîé
ðàâíû +1, åñëè âåðøèíà ñ íîìåðîì, ñîâïàäàþùèì ñ íîìåðîì ñòðîêè, ÿâ-
ëÿåòñÿ íà÷àëüíîé âåðøèíîé äóãè ñ íîìåðîì, ñîâïàäàþùèì ñ íîìåðîì
ñòîëáöà, –1 - êîíå÷íîé âåðøèíîé è 0 - åñëè âåðøèíà è äóãà íå èíöèäåíò-
íû. Î÷åâèäíî ÷èñëî ñòðîê òàêîé ìàòðèöû ðàâíî ÷èñëó âåðøèí, à ÷èñëî
ñòîëáöîâ - ÷èñëó äóã.
Íàïðèìåð, ìàòðèöà èíöèäåíòíîñòè ãðàôà íà ðèñ.2.15:
B b
ij
= =
+
-
+ + + -
-
- +
1 1 0 0 0
0 1 1 1 1
0 0 1 0 0
0 0 0 1 1
. (2.265)
Òàê êàê êàæäàÿ äóãà, çà èñêëþ÷åíèåì ïåòåëü, èíöèäåíòíà äâóì âåðøè-
íàì, òî êàæäûé ñòîëáåö ìàòðèöû ëèáî ñîäåðæèò ïàðó ýëåìåíòîâ +1 è -1,
ëèáî òîëüêî îäèí ýëåìåíò +1 (äëÿ ïåòåëü). Ó íåîðèåíòèðîâàííîãî ãðàôà
ìàòðèöà ñîäåðæèò ýëåìåíòû ñî çíà÷åíèÿìè òîëüêî 0 è +1.
Ìàòðèöåé äîñòèæèìîñòè íàçûâàåòñÿ ìàòðèöà, ýëåìåíòû êîòîðîé ðàâ-
íû 1, åñëè âåðøèíà ñ íîìåðîì, ðàâíûì íîìåðó ñòîëáöà, äîñòèæèìà èç âåð-
øèíû ñ íîìåðîì, ðàâíûì íîìåðó ñòðîêè, è 0 - åñëè íå äîñòèæèìà. Î÷å-
âèäíî ÷èñëî ñòðîê è ñòîëáöîâ òàêîé ìàòðèöû ðàâíî ÷èñëó âåðøèí ãðàôà.

77
Äëÿ ãðàôà íà ðèñ.2.15 ìàòðèöà äîñòèæèìîñòè èìååò âèä:
R r
ij
= =
1000
1111
0010
1111
. (2.266)
Ìàòðèöà äîñòèæèìîñòè ñâÿçíîãî íåîðèåíòèðîâàííîãî ãðàôà ñîäåðæèò òîëüêî ýëå-
ìåíòû, ðàâíûå 1.
2.8. Элементы комбинаторики [2,8,10]
Íàäåæíîñòü òåõíè÷åñêîãî îáúåêòà, ñîñòîÿùåãî èç áîëüøîãî ÷èñëà ñî-
ñòàâíûõ ÷àñòåé (ýëåìåíòîâ), îïðåäåëÿåòñÿ åãî ñòðóêòóðîé è íàäåæíîñòüþ
ýëåìåíòîâ. Ïîêàçàòåëè íàäåæíîñòè ðàññ÷èòûâàþòñÿ èñõîäÿ èç âåðîÿòíî-
ñòåé ðàçëè÷íûõ ñî÷åòàíèé (êîìáèíàöèé) ðàáîòîñïîñîáíûõ è íåðàáîòîñïî-
ñîáíûõ ñîñòîÿíèé ýëåìåíòîâ ñ èñïîëüçîâàíèåì ìåòîäîâ êîìáèíàòîðèêè.
Êîìáèíàòîðèêà èçó÷àåò ðàñïîëîæåíèÿ ýëåìåíòîâ ìíîæåñòâ â ñîîò-
âåòñòâèè ñî ñïåöèàëüíûìè ïðàâèëàìè è ìåòîäû ðàñ÷åòà âñåõ âîçìîæíûõ
ñïîñîáîâ, êîòîðûìè ýòè ðàñïîëîæåíèÿ ìîãóò áûòü îñóùåñòâëåíû.  êà÷å-
ñòâå ýëåìåíòîâ ìíîæåñòâ ìîãóò ðàññìàòðèâàòüñÿ êàê ïðåäìåòû, òàê è ñî-
áûòèÿ, íàïðèìåð, ïîñëåäîâàòåëüíîñòü îòêàçîâ óçëîâ è äåòàëåé òåõíè÷åñêî-
ãî óñòðîéñòâà - óïîðÿäî÷åííîå ìíîæåñòâî ñîáûòèé.
Ðàçìåùåíèÿìè íàçûâàþòñÿ óïîðÿäî÷åííûå ìíîæåñòâà ýëåìåíòîâ, îò-
ëè÷àþùèåñÿ äðóã îò äðóãà íàáîðîì ýëåìåíòîâ èëè èõ ïîðÿäêîì. Íàïðèìåð,
âîçìîæíûå ðàçìåùåíèÿ èç 3 ýëåìåíòîâ (A, B è Ñ) ïî 2: AB, AC, BC, BA,
CA è CB. ×èñëî âñåõ âîçìîæíûõ ïåðåìåùåíèé èç n ðàçëè÷íûõ ýëåìåíòîâ
ïî m ýëåìåíòîâ
( ) ( )
( ) ( )
A nn n m
n
nm
n
nm
n
m
= - - + =
×
×
×
××× -
=
-
1 1
12
12
...
...
...
.
!
!
(2.267)
Ïåðåñòàíîâêàìè íàçûâàþòñÿ óïîðÿäî÷åííûå ìíîæåñòâà ýëåìåíòîâ,
îòëè÷àþùèåñÿ äðóã îò äðóãà òîëüêî ïîðÿäêîì. Íàïðèìåð, âîçìîæíûå ïå-
ðåñòàíîâêè èç 3 ýëåìåíòîâ: ABC, BCA, CAB, CBA, BAC è ACB. ×èñëî
âñåõ âîçìîæíûõ ïåðåñòàíîâîê èç n ðàçëè÷íûõ ýëåìåíòîâ
P
n
= 1×2×...×n = A
n
n
= n! . (2.268)
Åñëè ñðåäè ýëåìåíòîâ èìåþòñÿ îäèíàêîâûå, òî
P
P
PPP
n
abc
n
n
a
b
c
¢
=
× × ×
=
× × ×...
,
!
! ! !...
(2.269)
ãäå a, b, c è ò.ä. - ÷èñëî îäèíàêîâûõ ýëåìåíòîâ A, B, C è ò.ä.
Ñî÷åòàíèÿìè íàçûâàþòñÿ ìíîæåñòâà ýëåìåíòîâ, îòëè÷àþùèåñÿ äðóã
îò äðóãà òîëüêî íàáîðîì ýëåìåíòîâ. Íàïðèìåð, âîçìîæíûå ñî÷åòàíèÿ èç 3
ýëåìåíòîâ ïî 2: AB, AC è BC. ×èñëî âñåõ âîçìîæíûõ ñî÷åòàíèé èç n
ðàçëè÷íûõ ýëåìåíòîâ ïî m ýëåìåíòîâ
(
)
(
)
( )
C
nn n m
m
A
P
n
mn m
n
m
n
m
n
=
- - +
×××
= =
-
1 1
12
...
...
.
!
! !
(2.270)
Î÷åâèäíî C
n
1
= n, C
n
n
= C
n
0
= 1, C
n
n–m
= C
n
m
.
×èñëà C
n
m
ñîîòâåòñòâóþò êîýôôèöèåíòàì â ôîðìóëå áèíîìà Íüþòîíà
è íàçûâàþòñÿ áèíîìèàëüíûìè êîýôôèöèåíòàìè. Èõ çíà÷åíèÿ ìîãóò áûòü
îïðåäåëåíû òàêæå ïî òàáëèöå òðåóãîëüíèêà Ïàñêàëÿ (ñì.ïðèë.I).

78
Äëÿ áîëüøèõ ÷èñåë n ïðè ðàñ÷åòå ôóíêöèè n! â ôîðìóëàõ (2.267)-(2.270) ìîæíî
òàêæå âîñïîëüçîâàòüñÿ ôîðìóëîé Ñòèðëèíãà:
( ) ( )
n
n
e
n n n n n
n
! !»
æ
è
ç
ö
ø
÷
» +
æ
è
ç
ö
ø
÷
- +2
1
2
1
2
2p p, ln ln ln .
(2.271)
Ëèòåðàòóðà
1. Íàäåæíîñòü è ýôôåêòèâíîñòü â òåõíèêå: Ñïðàâî÷íèê:  10 ò. Ò.2. Ìàòåìàòè÷å-
ñêèå ìåòîäû â òåîðèè íàäåæíîñòè è ýôôåêòèâíîñòè.-Ì.: Ìàøèíîñòðîåíèå,1987.- 280 ñ.
2. Ãèõìàí È.È., Ñêîðîõîä À.Â., ßäðåíêî Ì.È. Òåîðèÿ âåðîÿòíîñòåé è ìàòåìàòè-
÷åñêàÿ ñòàòèñòèêà.- Êèåâ: Âèùà øêîëà, 1988.- 439 ñ.
3. Èâàíîâà Â.Ì. è äð. Ìàòåìàòè÷åñêàÿ ñòàòèñòèêà.-Ì.: Âûñø.øêîëà, 1975.- 398 ñ.
4. Èâàøåâ-Ìóñàòîâ Î.Ñ. Òåîðèÿ âåðîÿòíîñòåé è ìàòåìàòè÷åñêàÿ ñòàòèñòèêà.- Ì.:
Íàóêà, 1979.- 256 ñ.
5. Âåíòöåëü Å.Ñ., Îâãàðîâ Ë.À. Òåîðèÿ âåðîÿòíîñòåé.- Ì.: Íàóêà, 1973.- 260 ñ.
6. Íàäåæíîñòü òåõíè÷åñêèõ ñèñòåì: Ñïðàâî÷íèê / Ïîä ðåä. È.À.Óøàêîâà.- Ì.: Ðà-
äèî è ñâÿçü, 1985. - 608 ñ.
7. Áàðçèëîâè÷ Å.Þ. è äð. Âîïðîñû ìàòåìàòè÷åñêîé òåîðèè íàäåæíîñòè.- Ì.: Ðàäèî
è ñâÿçü, 1983.- 376 ñ.
8. Áðîíøòåéí È.Í., Ñåìåíäÿåâ Ê.À. Ñïðàâî÷íèê ïî ìàòåìàòèêå äëÿ èíæåíåðîâ è
ó÷àùèõñÿ âòóçîâ.- Ì.: Íàóêà, 1981.- 720 ñ.
9. Ãìóðìàí Â.Å. Òåîðèÿ âåðîÿòíîñòåé è ìàòåìàòè÷åñêàÿ ñòàòèñòèêà.- Ì.:
Âûñø.øêîëà, 1972.- 368 ñ.
10. Êîðí Ã., Êîðí Ò. Ñïðàâî÷íèê ïî ìàòåìàòèêå (äëÿ íàó÷íûõ ðàáîòíèêîâ è èíæå-
íåðîâ).- Ì.: Íàóêà, 1977.- 832 ñ.
11. Ðîçàíîâ Þ.À. Ââåäåíèå â òåîðèþ ñëó÷àéíûõ ïðîöåññîâ.-Ì.:Íàóêà, 1982.- 127 ñ.
12. Ãíåäåíêî Á.Â., Áåëÿåâ Þ.Ê., Ñîëîâüåâ À.Ä. Ìàòåìàòè÷åñêèå ìåòîäû â òåî-
ðèè íàäåæíîñòè: Îñíîâíûå õàðàêòåðèñòèêè íàäåæíîñòè è èõ ñòàòèñòè÷åñêèé àíàëèç.-
Ì.: Íàóêà, 1965.- 524 ñ.
13. Êîçëîâ Ì.À., Ïðîõîðîâ À.Â. Ââåäåíèå â ìàòåìàòè÷åñêóþ ñòàòèñòèêó.- Ì.: Èçä-
âî ÌÃÓ, 1987.- 263 ñ.
14. Êîâàëåíêî È.Í., Ôèëèïïîâà À.À. Òåîðèÿ âåðîÿòíîñòåé è ìàòåìàòè÷åñêàÿ ñòà-
òèñòèêà.- Ì.: Âûñø.øêîëà, 1982.- 256 c.
15. Áåññîíîâ À.À., Ìîðîç À.Â. Íàäåæíîñòü ñèñòåì àâòîìàòè÷åñêîãî ðåãóëèðîâà-
íèÿ.- Ë.: Ýíåðãîàòîìèçäàò, 1984.- 216 ñ.
16. Õàçîâ Á.Ô., Äèäóñåâ Á.À. Ñïðàâî÷íèê ïî ðàñ÷åòó íàäåæíîñòè ìàøèí íà ñòàäèè
ïðîåêòèðîâàíèÿ.- Ì.: Ìàøèíîñòðîåíèå, 1986.- 224 ñ.
17. Êàïóð Å., Ëàìáåðñîí Ë. Íàäåæíîñòü è ïðîåêòèðîâàíèå ñèñòåì.- Ì.: Ìèð,
1980.- 604 ñ.
18. Õàí Ã., Øàïèðî Ñ. Ñòàòèñòè÷åñêèå ìîäåëè â èíæåíåðíûõ çàäà÷àõ.- Ì.: Ìèð,
1969.- 396 ñ.
19. Õèììåëüáëàó Ä. Àíàëèç ïðîöåññîâ ñòàòèñòè÷åñêèìè ìåòîäàìè.- Ì.: Ìèð, 1973.-
958 ñ.
20. Òðóõàíîâ Â.Ì. Ìåòîäû îáåñïå÷åíèÿ íàäåæíîñòè èçäåëèé ìàøèíîñòðîåíèÿ.- Ì.:
Ìàøèíîñòðîåíèå, 1995.- 304 ñ.
21. Ñîòñêîâ Á.Ñ. Îñíîâû òåîðèè è ðàñ÷åòà íàäåæíîñòè ýëåìåíòîâ è óñòðîéñòâ àâ-
òîìàòèêè è âû÷èñëèòåëüíîé òåõíèêè.- Ì.: Âûñø.øê., 1970.- 272 ñ.
22. Ñïðàâî÷íèê ïî íàäåæíîñòè. Òîì 1.- Ì.: Ìèð, 1969.- 340 ñ.
23. Áåëÿåâ Þ.Ê., Áîãàòûðåâ Â.À., Áîëîòèí Â.Â. è äð. Íàäåæíîñòü òåõíè÷åñêèõ
ñèñòåì: Ñïðàâî÷íèê.- Ì.: Ðàäèî è ñâÿçü, 1985.- 608
24. Êîëìîãîðîâ À.Í., Äðàãàëèí À.Ã. Ââåäåíèå â ìàòåìàòè÷åñêóþ ëîãèêó.- Ì.: Èçä-
âî ÌÃÓ, 1982.- 120 ñ.
25. Ìåíäåëüñîí Ý. Ââåäåíèå â ìàòåìàòè÷åñêóþ ëîãèêó.-Ì.: Íàóêà, 1976.- 320 ñ.
26. Íèêîëüñêàÿ È.Ë. Ìàòåìàòè÷åñêàÿ ëîãèêà.- Ì.: Âûñø.øêîëà, 1981.-127 ñ.
27. ßãëîì È.Ì. Áóëåâà ñòðóêòóðà è åå ìîäåëè.- Ì.: Ñîâ.ðàäèî, 1980.- 192 c.
28. Îðå Î. Òåîðèÿ ãðàôîâ.- Ì.: Íàóêà, 1980.- 336 ñ.
29. Óèëñîí Ð. Ââåäåíèå â òåîðèþ ãðàôîâ.- Ì.: Ìèð, 1977.- 208 ñ.
79
Глава 3.
ФИЗИЧЕСКИЕ ОСНОВЫ НАДЕЖНОСТИ
3.1. Физика отказов
Äëÿ îöåíêè íàäåæíîñòè òåõíè÷åñêèõ îáúåêòîâ èñïîëüçóåòñÿ, êàê ïðà-
âèëî, ìåòîäîëîãèÿ òåîðèè âåðîÿòíîñòåé è ìàòåìàòè÷åñêîé ñòàòèñòèêè [1-6].
 ýòîì ñëó÷àå âñå âîçìîæíûå ñîñòîÿíèÿ ýëåìåíòîâ è îáúåêòîâ ñâîäÿòñÿ,
êàê ïðàâèëî, ê äâóì - ðàáîòîñïîñîáíîìó è íåðàáîòîñïîñîáíîìó (ñîñòîÿíèþ
îòêàçà), ïîêàçàòåëÿì íàäåæíîñòè ïðèäàåòñÿ ñìûñë ôóíêöèé ñëó÷àéíîé âå-
ëè÷èíû (íàðàáîòêè äî îòêàçà), à ìîäåëÿì íàäåæíîñòè - ñìûñë ðàñïðåäåëå-
íèÿ ýòîé ñëó÷àéíîé âåëè÷èíû. Âåðîÿòíîñòíûå ìåòîäû íàõîäÿò ïðàêòè÷å-
ñêîå ïðèìåíåíèå ïðè îöåíêå ïîêàçàòåëåé íàäåæíîñòè ðàçëè÷íûõ òåõíè÷å-
ñêèõ ñèñòåì, àíàëèçå ïðîåêòíûõ âàðèàíòîâ, íàçíà÷åíèè îïòèìàëüíûõ ðåã-
ëàìåíòîâ ýêñïëóàòàöèè, ðàçðàáîòêå ïðîãðàìì èñïûòàíèé è êîíòðîëå êà÷å-
ñòâà ïðîäóêöèè.
Âåðîÿòíîñòíûé ïîäõîä ïðè îöåíêå íàäåæíîñòè òåõíè÷åñêèõ îáúåêòîâ
ó÷èòûâàåò ñòðóêòóðó ñëîæíûõ ñèñòåì êàê ñîåäèíåíèÿ ýëåìåíòîâ è íå êàñà-
åòñÿ ôèçè÷åñêî-õèìè÷åñêèõ ñâîéñòâ ìàòåðèàëà ýëåìåíòîâ, íå ó÷èòûâàåò ôè-
çè÷åñêóþ ïðèðîäó èõ âçàèìîäåéñòâèÿ è ïðîöåññîâ, ïðîèñõîäÿùèõ â ýëåìåí-
òàõ ïîä âîçäåéñòâèåì âíåøíèõ è âíóòðåííèõ ôàêòîðîâ è ïðèâîäÿùèõ ê èõ
îòêàçàì.  ñâÿçè ñ ýòèì âåðîÿòíîñòíûé ïîäõîä è ïðèìåíåíèå ñòàòèñòè÷å-
ñêîé òåîðèè íàäåæíîñòè èìååò ðÿä ïðèíöèïèàëüíûõ îãðàíè÷åíèé [7,8]:
- íåâîçìîæíîñòü ïðèìåíåíèÿ äëÿ àíàëèçà íàäåæíîñòè åäèíè÷íûõ îáú-
åêòîâ (íàïðèìåð äëÿ íåêîòîðûõ òåõíè÷åñêèõ ñèñòåì, íå èìåþùèõ àíàëî-
ãîâ, íà ñòàäèè ïðîåêòèðîâàíèÿ íîâîãî èçäåëèÿ);
- íåâîçìîæíîñòü â áîëüøèíñòâå ñëó÷àåâ îïðåäåëåíèÿ âèäà îòêàçà èñõî-
äÿ òîëüêî èç ôîðìàëüíî-ìàòåìàòè÷åñêèõ ãèïîòåç;
- íåâîçìîæíîñòü ó÷åòà âëèÿíèÿ ðàçëè÷íûõ âíåøíèõ âîçäåéñòâèé (ìå-
õàíè÷åñêèõ, õèìè÷åñêèõ, ýëåêòðè÷åñêèõ, òåïëîâûõ è äð.);
- íåâûïîëíèìîñòü â îáùåì ñëó÷àå ãèïîòåçû î íåèçìåííîé ïðèðîäå îò-
êàçà ïðè èçìåíåíèè óðîâíÿ íàãðóçêè íà îáúåêò;
- ñëîæíîñòü ó÷åòà íåñêîëüêèõ îäíîâðåìåííî ïðîòåêàþùèõ ïðîöåññîâ
ðàçðóøåíèÿ ñ ðàçëè÷íûìè ñêîðîñòÿìè (÷òî îáóñëàâëèâàåò íåëèíåéíîñòü
çàêîíîâ ñóììèðîâàíèÿ ïîâðåæäåíèé).
Ýòè îãðàíè÷åíèÿ, à òàêæå ïîâûøåíèå ñëîæíîñòè, ñíèæåíèå ìàòåðèàëî-
åìêîñòè è çàïàñîâ ïðî÷íîñòè òåõíè÷åñêèõ îáúåêòîâ, óñëîæíåíèå óñëîâèé
èõ ðàáîòû âûçâàëè íåîáõîäèìîñòü ðàçâèòèÿ ôèçè÷åñêîé òåîðèè íàäåæíî-
ñòè ("ôèçèêè îòêàçîâ"), êîòîðàÿ ðàññìàòðèâàåò äåòåðìèíèðîâàííûå èëè
ôóíêöèîíàëüíûå çàêîíîìåðíîñòè ôèçè÷åñêèõ ïðîöåññîâ, âëèÿþùèõ íà íà-
äåæíîñòü òåõíè÷åñêèõ îáúåêòîâ [7-9].
80
3.1.1. Основные положения физической теории надежности
 ïðîöåññå ýêñïëóàòàöèè òåõíè÷åñêèå îáúåêòû íàõîäÿòñÿ ïîä âîçäåé-
ñòâèåì áîëüøîãî ÷èñëà âíóòðåííèõ è âíåøíèõ ôàêòîðîâ, â ìàòåðèàëàõ
ýëåìåíòîâ ïðîèñõîäÿò ðàçëè÷íûå îáðàòèìûå è íåîáðàòèìûå ôèçèêî-
õèìè÷åñêèå ïðîöåññû è ÿâëåíèÿ, êîíå÷íûì ðåçóëüòàòîì êîòîðûõ ÿâëÿåòñÿ
îòêàç. Ñîñòîÿíèå îáúåêòà è åãî ïàðàìåòðû X
i
, îïðåäåëÿþùèå ñâîéñòâà íà-
äåæíîñòè (íàïðèìåð, çàïàñ ìåõàíè÷åñêîé, ýëåêòðè÷åñêîé èëè òåïëîâîé
ïðî÷íîñòè), ÿâëÿþòñÿ ôóíêöèåé âõîäíûõ ïàðàìåòðîâ Z
j
è âðåìåíè (èëè
íàðàáîòêè) t
X
i
= f(Z
1
, Z
2
, ..., Z
k
, t), (3.1)
ïðè÷åì â ÷èñëå ïàðàìåòðîâ Z
j
ó÷èòûâàþòñÿ ïàðàìåòðû, õàðàêòåðèçóþùèå
óñëîâèÿ ýêñïëóàòàöèè (íàãðóçêè, òåìïåðàòóðà, õàðàêòåðèñòèêè ñðåäû è
ò.ä.), ñîñòîÿíèå ìàòåðèàëà (ìåõàíè÷åñêèå, ýëåêòðè÷åñêèå, ìàãíèòíûå è
äðóãèå ñâîéñòâà) è äðóãèå ôàêòîðû.
Îäíàêî ïðè íàëè÷èè òîëüêî ôóíêöèîíàëüíîé çàâèñèìîñòè (3.1), äàæå
äîñòàòî÷íî äîñòîâåðíî îïèñûâàþùåé ñîñòîÿíèå è ôóíêöèîíèðîâàíèå îáú-
åêòà, íåëüçÿ òî÷íî ïðåäñêàçàòü åãî ïîâåäåíèå è ìîìåíò îòêàçà, òàê êàê
ñàìè àðãóìåíòû Z
1
, Z
2
, ..., Z
k
è, òåì áîëåå, îïðåäåëÿþùèå ïàðàìåòðû X
i
ÿâëÿþòñÿ, êàê ïðàâèëî, ñëó÷àéíûìè èëè ïîëóñëó÷àéíûìè âåëè÷èíàìè.
Äåéñòâèòåëüíî, â ïðîöåññå ýêñïëóàòàöèè îáû÷íî ïðîèñõîäÿò íåïðåäâèäåí-
íûå ñëó÷àéíûå èçìåíåíèÿ è êîëåáàíèÿ íàãðóçîê è óñëîâèé ýêñïëóàòàöèè,
ýëåìåíòû îáúåêòîâ ìîãóò áûòü èçãîòîâëåíû ñ ðàçëè÷íûìè äîïóñêàìè íà
ãåîìåòðè÷åñêèå ðàçìåðû, îòêëîíåíèÿìè òåõíîëîãè÷åñêèõ ïàðàìåòðîâ, ñî-
ñòàâà, ñòðóêòóðû è ñâîéñòâ ìàòåðèàëîâ è ò.ä. Êðîìå òîãî, áîëüøèíñòâî
ôèçè÷åñêèõ ïðîöåññîâ è ÿâëåíèé, ïðîèñõîäÿùèõ â ìàòåðèàëàõ, èìåþò ôè-
çèêî-ñòàòèñòè÷åñêóþ ïðèðîäó. Ñëåäîâàòåëüíî, ïîäõîä ê àíàëèçó ñîñòîÿíèÿ
òåõíè÷åñêèõ îáúåêòîâ äîëæåí áûòü, êàê ïðàâèëî, ñòðóêòóðíî-âåðîÿòíîñò-
íûì, ò.å. äîëæåí ó÷èòûâàòü êàê ôèçè÷åñêóþ ñòðóêòóðó îáúåêòîâ è ìàòå-
ðèàëîâ, òàê è ñòàòèñòè÷åñêèå êèíåòè÷åñêèå çàêîíîìåðíîñòè ïðîöåññîâ [10].
Ôóíêöèîíàëüíûå çàâèñèìîñòè âèäà (3.1) õîòÿ è çíà÷èòåëüíî èäåàëèçè-
ðóþò ðåàëüíûå ïðîöåññû è ëèøü ñ èçâåñòíîé ñòåïåíüþ ïðèáëèæåíèÿ îò-
ðàæàþò èõ ôèçè÷åñêóþ ñóùíîñòü, íî ïîçâîëÿþò ïðåäñêàçûâàòü âîçìîæíûé
îáùèé õîä ïðîöåññîâ ïðè ðàçëè÷íûõ óñëîâèÿõ. Òàê, íàïðèìåð, ïîäñòàíîâêà
â óðàâíåíèå (3.1) ñðåäíèõ çíà÷åíèé àðãóìåíòîâ Z
1
, Z
2
, ..., Z
k
äàåò îöåíêó
ìàòåìàòè÷åñêîãî îæèäàíèÿ ïàðàìåòðà X
i
, à èñõîäÿ èç äèñïåðñèé ñëó÷àé-
íûõ àðãóìåíòîâ ìîæíî îöåíèòü åãî äèñïåðñèþ ïàðàìåòðà. Ïîýòîìó ôèçè-
÷åñêàÿ òåîðèÿ íàäåæíîñòè ("ôèçèêà îòêàçîâ"), èçó÷àþùàÿ çàêîíîìåðíîñòè
èçìåíåíèÿ ñâîéñòâ ìàòåðèàëîâ è ýëåìåíòîâ òåõíè÷åñêèõ ñèñòåì â óñëîâè-
ÿõ ýêñïëóàòàöèè, ÿâëÿåòñÿ îñíîâîé äëÿ èçó÷åíèÿ è îöåíêè õàðàêòåðèñòèê
íàäåæíîñòè è ïîñòðîåíèÿ ìàòåìàòè÷åñêèõ ìîäåëåé îòêàçîâ [8].
Âûðàáîòêà ðåñóðñà èçäåëèé è âîçíèêíîâåíèå îòêàçîâ ñâÿçàíû, ãëàâíûì
îáðàçîì, ñ íàêîïëåíèåì íåîáðàòèìûõ ïîâðåæäåíèé è èçìåíåíèåì (ñòàðå-
íèåì) èõ ýëåìåíòîâ (äåòàëåé è óçëîâ). Îïðåäåëÿþùåå âëèÿíèå íà ñòàðå-
íèå îêàçûâàþò ðàçëè÷íûå ôèçèêî-õèìè÷åñêèå ïðîöåññû è ÿâëåíèÿ. Ïî-
âðåæäåíèÿ ìîãóò áûòü êàê ìåõàíè÷åñêîãî (óñòàëîñòü, òðåùèíîîáðàçîâàíèå,
èçíîñ, íàêîïëåíèå ïëàñòè÷åñêèõ äåôîðìàöèé è ò.ä.), òàê è ôèçèêî-
