Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1

41

è ñðåäíåé íàðàáîòêå t = 1/l. Äîñòîèíñòâîì ðàñïðåäåëåíèÿ ÿâëÿåòñÿ åãî

ïðîñòîòà, áëàãîäàðÿ ÷åìó íåêîòîðûå çàäà÷è äîïóñêàþò àíàëèòè÷åñêèå ðå-

øåíèÿ.

Ýêñïîíåíöèàëüíîå ðàñïðåäåëåíèå çàäàåòñÿ èíòåãðàëüíîé ôóíêöèåé èëè

ïëîòíîñòüþ ðàñïðåäåëåíèÿ

F(x) = 1 - exp(-lx), f(x) = lexp(-lx), x ³ 0, (2.72)

ãäå l - ïàðàìåòð ðàñïðåäåëåíèÿ, êîòîðûé â òåîðèè íàäåæíîñòè èìååò ñìûñë èíòåíñèâ-

íîñòè îòêàçîâ.

Ïðè lx£0,1 ôîðìóëó ðàñïðåäåëåíèÿ ïîñëå åå ðàçëîæåíèÿ â ðÿä ìîæíî çàìåíèòü

ïðèáëèæåííîé ôîðìóëîé

( )

( ) ( )

Fx x

x x

x= - - + - +

é

ë

ê

ù

û

ú

»1 1

2 3

l

l l

l

! !

...

, (2.73)

êîòîðàÿ ÷àñòî èñïîëüçóåòñÿ ïðè ïðèáëèæåííûõ ðàñ÷åòàõ ïàðàìåòðîâ íàäåæíîñòè.

Îñíîâíûå ñâîéñòâà ýêñïîíåíöèàëüíîãî ðàñïðåäåëåíèÿ:

M(x) = 1/l, D(x) = 1/l

2

, v = 1. (2.74)

Ýêñïîíåíöèàëüíîå ðàñïðåäåëåíèå ìîæíî ñ÷èòàòü ÷àñòíûì ñëó÷àåì ðàñïðåäåëåíèÿ

Âåéáóëëà è ãàììà-ðàñïðåäåëåíèÿ.

Íîðìàëüíîå ðàñïðåäåëåíèå (ðàñïðåäåëåíèå Ãàóññà) ÷àñòî èñïîëüçóåòñÿ

äëÿ îïèñàíèÿ èçíîñîâûõ îòêàçîâ èëè â ñëó÷àÿõ, êîãäà îòêàç ìîæåò áûòü

ñëåäñòâèåì áîëüøîãî ÷èñëà ðàçëè÷íûõ ïðè÷èí. Îíî ìîæåò ñ÷èòàòüñÿ ïðå-

0,2

0,4

0,6

0,8

0

0,2

0,4

0,6

0,8

x-a

F

(

x

)

b-a

0

a

b

x

f

(

x

)

1

b-a

à) á)

Ðèñ.2.1. Èíòåãðàëüíàÿ (à) è äèôôåðåíöèàëüíàÿ (á) ôóíêöèè

ðàâíîìåðíîãî ðàñïðåäåëåíèÿ

0,2

0,4

0,6

0,8

0

1

2

3

4

lx

f(x)

lx

0

1

2

-1

-2-3

f(x)

x-m

s

0,1

0,2

0,3

Ðèñ.2.2. Ýêñïîíåíöèàëüíîå ðàñïðåäåëåíèå. Ðèñ.2.3. Íîðìàëüíîå ð

àñïðåäåë

å

íèå

42

äåëüíûì äëÿ ìíîãèõ ðàñïðåäåëåíèé ñëó÷àéíûõ âåëè÷èí - ðàñïðåäåëåíèÿ

Ïóàññîíà, áèíîìèàëüíîãî, ãàììà-ðàñïðåäåëåíèÿ è äð.

Íîðìàëüíîå ðàñïðåäåëåíèå çàäàåòñÿ èíòåãðàëüíîé ôóíêöèåé èëè ïëîò-

íîñòüþ ðàñïðåäåëåíèÿ (ðèñ.2.3)

( )

Fx

x

dx fx

x

= -

-

é

ë

ê

ù

û

ú

= -

-

é

ë

ê

ù

û

ú

-¥

ò

1

2

1

2

s p

m

s

s p

m

s

exp , exp , (2.75)

ãäå –¥ < x < ¥.

Äëÿ íîðìàëüíîãî ðàñïðåäåëåíèÿ M(x) = m, D(x) = s

2

, v = s/m, ïàðà-

ìåòðû -¥<m<+¥ è s>0 - ïàðàìåòðû ñäâèãà è ìàñøòàáà (ðèñ.2.4).

Íîðìàëüíîå ðàñïðåäåëåíèå ÷àñòî çàäàåòñÿ òàêæå íîðìèðîâàííîé ôóíêöèåé Ëàïëàñà

Ô(z) èëè ïëîòíîñòüþ ðàñïðåäåëåíèÿ j(z) äëÿ öåíòðèðîâàííîé è íîðìèðîâàííîé ñëó-

÷àéíîé âåëè÷èíû z = (x – m )/s :

() ()

Ôz

z

dz, z

z

= -

æ

è

ç

ö

ø

÷

= -

æ

è

ç

ö

ø

÷

ò

1

2 2

1

2 2

2

0

2

p

j

p

exp exp .

(2.76)

Çíà÷åíèÿ ôóíêöèè Ô(z) òàáóëèðîâàíû (ñì.ïðèë.I). Òàáëè÷íîå çíà÷åíèå èíòåãðàëà

Ô(x) ÷èñëåííî ðàâíî ïëîùàäè ôèãóðû ìåæäó êðèâîé ðàñïðåäåëåíèÿ (ðèñ.2.2) è îñüþ

àáñöèññ è îãðàíè÷åííîé îñüþ ñèììåòðèè êðèâîé è îðäèíàòîé ñî çíà÷åíèåì x.

Ôóíêöèè Ô(z) è F(x) ñâÿçàíû ñîîòíîøåíèÿìè:

F(x) = 1/2 + Ô(z), Ô(-z) = -Ô(z). (2.77)

Íîðìàëüíîå ðàñïðåäåëåíèå çàäàåòñÿ òàêæå çíà÷åíèÿìè êâàíòèëåé u

p

óðîâíÿ p

(ïðèë.I), ïî êîòîðûì ìîæíî îïðåäåëèòü âåðîÿòíîñòü çàäàííîãî çíà÷åíèÿ ñëó÷àéíîé âå-

ëè÷èíû x:

x

p

= M(x) + u

p

s. (2.78)

Äëÿ íîðìàëüíî ðàñïðåäåëåííîé ñëó÷àéíîé âåëè÷èíû âåðîÿòíîñòü ïîïàäàíèÿ â ïðå-

äåëû èíòåðâàëà, îãðàíè÷åííîãî òî÷êàìè, ðàñïîëîæåííûìè íà ðàññòîÿíèè s îò ìàòåìà-

òè÷åñêîãî îæèäàíèÿ, ñîñòàâëÿåò 0,6813, èíòåðâàëà îò M(x)-2s äî M(x)+2s - 0,9544 è

îò M(x)-3s äî M(x)+3s - 0,9973, ò.å. ñ âåðîÿòíîñòüþ 99,73% ìîæíî ñ÷èòàòü, ÷òî

M(x) - 3s £ x £ M(x) + 3s. (2.79)

Óñå÷åííîå íîðìàëüíîå ðàñïðåäåëåíèå ïîëó÷àåòñÿ èç íîðìàëüíîãî ïðè

îãðàíè÷åíèè èíòåðâàëà èçìåíåíèÿ ñëó÷àéíîé âåëè÷èíû òîëüêî ïîëîæè-

òåëüíûìè çíà÷åíèÿìè. Îíî âíîñèò óòî÷íåíèå â ðàñ÷åòû íàäåæíîñòè ïî

ñðàâíåíèþ ñ íîðìàëüíûì ðàñïðåäåëåíèåì ïðè áîëüøèõ çíà÷åíèÿõ êîýôôè-

öèåíòà âàðèàöèè v = s/m.

f(x)

x

f(x)

x

M

1

(x)=M

2

(x)=M

3

(x)

s

1

(x)<

s

2

(x)<

s

3

(x)

s

1

(x)

s

2

(x)

s

3

(

x

)

M(x)

s

1

(x)=

s

2

(x), M

1

(x)<M

2

(x)

M

1

(x) M

2

(x)

à) á)

Ðèñ.2.4. Ïëîòíîñòü âåðîÿòíîñòè íîðìàëüíîãî ðàñïðåäåëåíèÿ ïðè ðàçëè÷íûõ çíà÷åíèÿõ

ìàòåìàòè÷åñêîãî îæèäàíèÿ (à) è ñðåäíåãî êâàäðàòè÷åñêîãî

îòêëîíåíèÿ (á)

43

Ôóíêöèÿ ïëîòíîñòè âåðîÿòíîñòè óñå÷åííîãî íîðìàëüíîãî ðàñïðåäåëåíèÿ çàïèñûâà-

åòñÿ àíàëîãè÷íî íîðìàëüíîìó ðàñïðåäåëåíèþ (2.75), íî ñ êîýôôèöèåíòîì ïðîïîðöèî-

íàëüíîñòè c:

( )

fx

c

x x

= -

-

é

ë

ê

ù

û

ú

s p

s

2

0

2

exp

, (2.80)

ãäå x

0

- çíà÷åíèå, ñîîòâåòñòâóþùåå ìàêñèìóìó ôóíêöèè f(x), ò.å. ìîäà.

Êîýôôèöèåíò c äëÿ ðàñïðåäåëåíèÿ, îãðàíè÷åííîãî ïðåäåëàìè èçìåíåíèÿ x îò a äî

b, îïðåäåëÿåòñÿ èç óñëîâèÿ

( ) () ()

[ ]

fxdx cFb Fa

a

b

ò

= - =1

, (2.81)

îòêóäà

() ()

c

Fb Fa

Ô

b x

Ô

a x

=

-

=

-

æ

è

ç

ö

ø

÷

-

æ

è

ç

ö

ø

÷

1 1

0 0

s s

, (2.82)

ãäå F(a) è F(b) - çíà÷åíèÿ èíòåãðàëüíîé ôóíêöèè íîðìàëüíîãî ðàñïðåäåëåíèÿ äëÿ ïðå-

äåëüíûõ çíà÷åíèé x.

Óñå÷åííîå íîðìàëüíîå ðàñïðåäåëåíèå â îñíîâíîì èñïîëüçóåòñÿ ñ ïðåäåëüíûìè çíà-

÷åíèÿìè a = 0 è b = ¥ (â çàäà÷àõ íàäåæíîñòè ýòî îçíà÷àåò íåâîçìîæíîñòü îòêàçîâ ïðè

îòðèöàòåëüíûõ çíà÷åíèÿõ âðåìåíè). Ïîñêîëüêó Ô(¥) = 0,5 è Ô(–z) = Ô(z), òî äëÿ ýòî-

ãî ñëó÷àÿ ôîðìóëà (2.82) ïðèíèìàåò âèä

( )

c

Ô Ô

x

Ô

x

=

¥- -

æ

è

ç

ö

ø

÷

=

+

æ

è

ç

ö

ø

÷

1 1

05

0 0

s s

,

. (2.83)

Òàêèì îáðàçîì, äëÿ îïðåäåëåíèÿ êîýôôèöèåíòà c ìîæíî èñïîëüçîâàòü òàáëèöû ôóíê-

öèè Ëàïëàñà èëè êâàíòèëåé íîðìàëüíîãî ðàñïðåäåëåíèÿ (ïðèë.I).

Ïðè 0 £ x £ ¥ õàðàêòåðèñòèêè óñå÷åííîãî íîðìàëüíîãî ðàñïðåäåëåíèÿ

( ) ( ) ( )

(

)

Mx Mx k Dx k k

Mx

= + = = - -

é

ë

ê

ù

û

ú

s s s

s

,

2 2 2

1

, (2.84)

ãäå

`

M(x),

`

D(x) è`s - ìàòåìàòè÷åñêîå îæèäàíèå, äèñïåðñèÿ è ñðåäíåå êâàäðàòè÷åñêîå

îòêëîíåíèå äëÿ óñå÷åííîãî íîðìàëüíîãî ðàñïðåäåëåíèÿ, M(x), D(x) è s - òå æå ïàðà-

ìåòðû äëÿ íîðìàëüíîãî ðàñïðåäåëåíèÿ,

( )

k

c

Mx

= -

é

ë

ê

ù

û

ú

2

p

s

exp

. (2.85)

Àíàëèç ôîðìóëû (2.83) ïîêàçûâàåò, ÷òî ïðè x

0

> 2s, ÷òî îáû÷íî èìååò ìåñòî íà

ïðàêòèêå, êîýôôèöèåíò c î÷åíü íåçíà÷èòåëüíî îòëè÷àåòñÿ îò åäèíèöû (ñ » 1), â ñâÿçè

ñ ÷åì íåîáõîäèìîñòü ó÷åòà óñå÷åíèÿ íîðìàëüíîãî ðàñïðåäåëåíèÿ, ñâÿçàííîãî ñ îãðàíè-

÷åíèåì èíòåðâàëà èçìåíåíèÿ ñëó÷àéíîé âåëè÷èíû, îòïàäàåò. Ïðè ýòîì

`

M(x) » M(x) è

s » s.

Äëÿ óñå÷åííîãî íîðìàëüíîãî ðàñïðåäåëåíèÿ èíòåãðàëüíàÿ ôóíêöèÿ

( )

Fx c Ô

x x

= +

-

æ

è

ç

ö

ø

÷

é

ë

ê

ù

û

ú

1

2

0

s

. (2.86)

Ëîãàðèôìè÷åñêè íîðìàëüíîå ðàñïðåäåëåíèå õàðàêòåðèçóåò ñëó÷àéíûå

âåëè÷èíû, ëîãàðèôì êîòîðûõ ðàñïðåäåëåí ïî íîðìàëüíîìó çàêîíó:

( )

Fx

x

dxfx

x

= -

-

é

ë

ê

ù

û

ú

= -

-

é

ë

ê

ù

û

ú

>

ò

1

2

1

2

1

2

0

2

0

2

s p

m

s

s p

m

s

exp

ln

, exp

ln

, . (2.87)

Äëÿ ëîãàðèôìè÷åñêè íîðìàëüíîãî ðàñïðåäåëåíèÿ (ðèñ.2.5)

( ) ( )

[ ]

( )

Mx Dx v= +

æ

è

ç

ö

ø

÷

= + - = -exp , exp exp , expm

s

m s s s

2

2 2 2

2

2 1 1

. (2.88)

44

Äëÿ âû÷èñëåíèÿ ôóíêöèé ëîãàðèôìè÷åñêè íîðìàëüíîãî ðàñïðåäåëåíèÿ ìîæíî ïîëü-

çîâàòüñÿ òàáëèöàìè íîðìàëüíîãî ðàñïðåäåëåíèÿ, ò.ê.

( ) ( )

Fx Ô

x

fx

x

=

-

æ

è

ç

ö

ø

÷

=

-

æ

è

ç

ö

ø

÷

ln

,

ln

.

m

s s

j

m

s

1

(2.89)

Â òåîðèè íàäåæíîñòè ëîãàðèôìè÷åñêè íîðìàëüíîå ðàñïðåäåëåíèå èñ-

ïîëüçóåòñÿ äëÿ îïèñàíèÿ íàðàáîòêè äî îòêàçà ýëåìåíòîâ â ïåðèîä íàñòóï-

ëåíèÿ óñòàëîñòè ìàòåðèàëîâ è èçíîñîâûõ îòêàçîâ, à òàêæå íàðàáîòêè íå-

êîòîðûõ ñëîæíûõ òåõíè÷åñêèõ ñèñòåì.

Ðàñïðåäåëåíèå Âåéáóëëà (ðèñ.2.6) â òåîðèè íàäåæíîñòè èñïîëüçóåòñÿ

äëÿ îïèñàíèÿ îòêàçîâ îáúåêòîâ ñ ìîíîòîííîé èíòåíñèâíîñòüþ è îáëàäàåò

áîëüøèì ðàçíîîáðàçèåì ôîðì. Îíî ìîæåò çàäàâàòüñÿ â âèäå:

( ) ( )

Fx

x

a

fx

b

a

x

a

x

a

x

b b b

=- -

æ

è

ç

ö

ø

÷

é

ë

ê

ù

û

ú

=

æ

è

ç

ö

ø

÷

-

æ

è

ç

ö

ø

÷

é

ë

ê

ù

û

ú

³

-

1 0

1

exp , exp , , (2.90)

ãäå a > 0 è b > 0 - ïàðàìåòðû ìàñøòàáà è ôîðìû.

Îñîáåííîñòüþ ðàñïðåäåëåíèÿ Âåéáóëëà ÿâëÿåòñÿ òî, ÷òî ñ èçìåíåíèåì

ïàðàìåòðà ôîðìû b èçìåíÿåòñÿ è âèä ãðàôèêà ôóíêöèè ïëîòíîñòè ðàñïðå-

äåëåíèÿ (ðèñ.2.6). Ýòî ñâîéñòâî ÷àñòî ïîçâîëÿåò ñîîòâåòñòâóþùèì ïîäáî-

ðîì ïàðàìåòðîâ îáåñïå÷èòü õîðîøåå ñîâïàäåíèå îïûòíûõ äàííûõ ñ àíàëè-

òè÷åñêèìè âûðàæåíèÿìè.

Îñíîâíûå õàðàêòåðèñòèêè ðàñïðåäåëåíèÿ Âåéáóëëà:

( ) ( )

( )

Mx aK Dx aC K v

C

K

= = - = -, , ,

2 2

2

1

(2.91)

ãäå K = G(1+1/b), C

2

= G(1+2/b)-K

2

,

() ( )

Gz u udu

z

= -

-

¥

ò

1

0

exp

- ãàììà-ôóíêöèÿ.

Ðàñïðåäåëåíèå Âåéáóëëà âêëþ÷àåò â ñåáÿ êàê ÷àñòíûå ñëó÷àè ýêñïîíåíöèàëüíîå ðàñ-

ïðåäåëåíèå (ïðè b=1) è ðàñïðåäåëåíèå Ðýëåÿ (b=2), ïðè b

³

3,5 áëèçêî ê íîðìàëüíîìó.

Èíîãäà èñïîëüçóåòñÿ ôîðìà çàïèñè, îòëè÷íàÿ îò ôîðìóë (2.90):

F(x) = 1 - exp(-lx

a

), f(x) = alx

a-

1

exp(-lx

a

). (2.92)

Î÷åâèäíî ïðè ýòîì a = b è l = (1/a)

b

.

Ãàììà-ðàñïðåäåëåíèå òàêæå äîñòàòî÷íî óíèâåðñàëüíî:

( )

Fx

ab

x

a

x

a

dx fx

ab

x

a

x

a

b

x

b

=

+

æ

è

ç

ö

ø

÷

-

æ

è

ç

ö

ø

÷

=

+

æ

è

ç

ö

ø

÷

-

æ

è

ç

ö

ø

÷

ò

1

0

G G

exp , exp . (2.93)

0

0,2

0,4

0,6

1

2

x/a

f(x)

b/a

b =

4

2

1

0,5

0

0,1

0,2

0,3

2

4

6

8

x

f

(

x

)

Ðèñ.2.5. Ëîãàðèôìè÷åñêè íîðìàëüíîå ðàñïðåäåëåíèå Ðèñ.2.6. Ðàñïðåäåëåíèå Âåéáóëëà

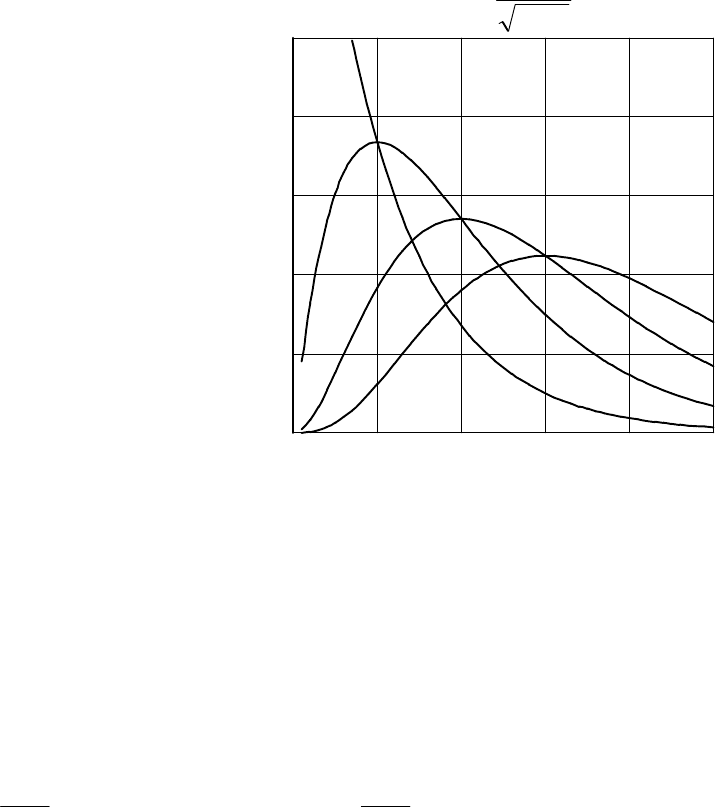
45

Ïàðàìåòðû a > 0 è b ³ –1 â ãàììà-ðàñïðåäåëåíèè ÿâëÿþòñÿ ïàðàìåòðà-

ìè ìàñøòàáà è ôîðìû (ðèñ.2.7).

Îñíîâíûå õàðàêòåðèñòèêè ãàììà-ðàñïðåäåëåíèÿ:

( ) ( ) ( ) ( )

Mx ab Dx ab v

b

= + = + =

+

1 1

1

2

, , . (2.94)

Ãàììà-ðàñïðåäåëåíèå õîðîøî

îïèñûâàåò íàðàáîòêó äî îòêàçà ìíî-

ãèõ íåâîññòàíàâëèâàåìûõ òåõíè÷å-

ñêèõ ñèñòåì. Åñëè íåçàâèñèìûå

ñëó÷àéíûå âåëè÷èíû x

i

èìåþò îäè-

íàêîâîå ýêñïîíåíöèàëüíîå ðàñïðå-

äåëåíèå, òî èõ ñóììà èìååò ãàììà-

ðàñïðåäåëåíèå, ïîýòîìó îíî ìîæåò

èñïîëüçîâàòüñÿ äëÿ îïèñàíèÿ ñèñ-

òåìû ñ ðåçåðâèðîâàíèåì ýëåìåíòîâ

çàìåùåíèåì.

Åñëè íåçàâèñèìûå ñëó÷àéíûå

âåëè÷èíû x

1

, x

2

, ..., x

n

ïîä÷èíÿþòñÿ

ãàììà-ðàñïðåäåëåíèþ ñ îäèíàêîâûì

ïàðàìåòðîì ìàñøòàáà a è ïàðàìåò-

ðàìè ôîðìû b

1

, b

2

, ..., b

n

, òî èõ

ñóììà òàêæå ïîä÷èíÿåòñÿ ãàììà-ðàñïðåäåëåíèþ ñ ïàðàìåòðàìè a è

b=b

1

+b

2

+...+b

n

+n-1.

Ïðè b=0 ãàììà-ðàñïðåäåëåíèå ñîâïàäàåò ñ ýêñïîíåíöèàëüíûì, ïðè

áîëüøèõ çíà÷åíèÿõ b ïðàêòè÷åñêè ñîâïàäàåò ñ íîðìàëüíûì. Ïðè öåëûõ

çíà÷åíèÿõ b ãàììà-ðàñïðåäåëåíèå íàçûâàåòñÿ ðàñïðåäåëåíèåì Ýðëàíãà.

Íàðÿäó ñ ôîðìóëàìè (2.93) èñïîëüçóåòñÿ äðóãàÿ ôîðìà çàïèñè ãàììà-ðàñïðå-

äåëåíèÿ:

( )

( ) ( )

( )

Fx x xdx fx x x

x

= - = -

- -

ò

l

a

l

a

l

a

G G

1

0

1

exp , exp

. (2.95)

Ïðè ýòîì a = b+1, l = 1/a.

2.2.5. Смеси распределений

×àñòî â ïðàêòè÷åñêèõ ñèòóàöèÿõ ñëó÷àéíàÿ âåëè÷èíà ÿâëÿåòñÿ ñìåñüþ

äâóõ èëè áîëåå ñëó÷àéíûõ âåëè÷èí ñ ðàçëè÷íûìè ðàñïðåäåëåíèÿìè.

Åñëè ôóíêöèè f

1

(x

1

), f

2

(x

1

), ..., f

n

(x

n

) ÿâëÿþòñÿ ôóíêöèÿìè ïëîòíîñòè

âåðîÿòíîñòè íåêîòîðûõ ñëó÷àéíûõ âåëè÷èí è ñóììà âåðîÿòíîñòåé ýòèõ âå-

ëè÷èí p

i

ðàâíà åäèíèöå (p

1

+p

2

+...+p

n

=1), òî ôóíêöèÿ

( )

( ) ( ) ( ) ( )

fx pfx pfx pfx pfx

nn n ii i

i

n

= + ++ =

=

å

11 1 22 2

1

... , (2.96)

ÿâëÿåòñÿ ïëîòíîñòüþ ñìåñè ðàñïðåäåëåíèé.

Ñîîòâåòñòâóþùàÿ èíòåãðàëüíàÿ ôóíêöèÿ èìååò âèä

( )

( ) ( ) ( ) ( )

Fx pFx pFx pFx pFx

nn n ii i

i

n

= + ++ =

=

å

11 1 22 2

1

... , (2.97)

ãäå F

i

(x

i

) - èíòåãðàëüíûå ôóíêöèè ðàñïðåäåëåíèé ïëîòíîñòè f

i

(x

i

).

0

0,1

0,2

0,3

0,4

1

2

3

4

b = 0

1

2

3

x

f(x)

Ðèñ.2.7. Ñòàíäàðòíîå ãàììà

-

ðàñïðåäåëåíèå

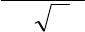
46

Èç ôîðìóëû (2.96) ñëåäóåò, ÷òî ìàòåìàòè÷åñêîå îæèäàíèå ñìåñè ðàñïðåäåëåíèé

( )

( ) ( ) ( ) ( )

Mx pMx pMx pMx pMx

n n n i i i

i

n

= + ++ =

=

å

111 2 2 2

1

...

. (2.98)

Îäíîé èç ïðàêòè÷åñêè âàæíûõ òåîðåì òåîðèè âåðîÿòíîñòåé ÿâëÿåòñÿ

öåíòðàëüíàÿ ïðåäåëüíàÿ òåîðåìà, ñîãëàñíî êîòîðîé ðàñïðåäåëåíèå ñóì-

ìû íåçàâèñèìûõ ñëó÷àéíûõ âåëè÷èí x = x

1

+x

2

+...+x

n

ñ ëþáûìè ðàñïðåäå-

ëåíèÿìè âåðîÿòíîñòåé ñòðåìèòñÿ â ïðåäåëå ê íîðìàëüíîìó çàêîíó ñ ìàòå-

ìàòè÷åñêèì îæèäàíèåì nm è äèñïåðñèåé ns

2

:

() ()

lim

n

Pa

x n

n

b Ôb Ôa

®¥

<

-

<

ì

í

î

ü

ý

þ

= -

m

s

. (2.99)

Öåíòðàëüíàÿ ïðåäåëüíàÿ òåîðåìà ÿâëÿåòñÿ òåîðåòè÷åñêîé îñíîâîé ïðè-

ìåíåíèÿ íîðìàëüíîãî ðàñïðåäåëåíèÿ ïðè ðåøåíèè ìíîãèõ çàäà÷ òåîðèè

íàäåæíîñòè, â ÷àñòíîñòè ïðè îïðåäåëåíèè íàðàáîòêè íà îòêàç â ðåçóëüòàòå

óñòàëîñòíûõ èçìåíåíèé è ïðè ðàñ÷åòàõ ïàðàìåòðîâ íàäåæíîñòè ìåòîäàìè

ñòàòèñòè÷åñêîãî ìîäåëèðîâàíèÿ.

2.2.6. Случайные векторы (многомерные случайные величины)

Äëÿ îïèñàíèÿ ñîâîêóïíîñòè n ñëó÷àéíûõ âåëè÷èí x

1

, x

2

, ..., x

n

(ò.å. n-

ìåðíîé ñëó÷àéíîé âåëè÷èíû èëè n-ìåðíîãî âåêòîðà) èñïîëüçóþòñÿ n-

ìåðíûå ôóíêöèè ðàñïðåäåëåíèÿ, ò.å. âåðîÿòíîñòè ñîâìåñòíîãî âûïîëíå-

íèÿ íåðàâåíñòâ x

i1

<x

1

, x

i2

<x

2

, ..., x

in

<x

n

:

F(x

1

,x

2

,...,x

n

) = p(x

i1

<x

1

,x

i2

<x

2

,...,x

in

<x

n

). (2.100)

Ôóíêöèþ F(x

1

,x

2

,...,x

n

) ÷àñòî òàêæå íàçûâàþò ðàñïðåäåëåíèåì âåêòî-

ðà (x

1

,x

2

,...,x

n

) èëè ñîâìåñòíûì ðàñïðåäåëåíèåì âåëè÷èí x

1

,x

2

,...,x

n

.

Åñëè ðàññìàòðèâàòü âåëè÷èíû x

1

,x

2

,...,x

n

êàê êîîðäèíàòû òî÷êè â n-

ìåðíîì ïðîñòðàíñòâå, òî ôóíêöèÿ F(x

1

,x

2

,...,x

n

) ñîîòâåòñòâóåò âåðîÿòíîñòè

íàõîæäåíèÿ òî÷êè â ïîëóîòêðûòîì ïàðàëëåëåïèïåäå

x

i1

<x

1

,x

i2

<x

2

,...,x

in

<x

n

. Âåðîÿòíîñòü òîãî, ÷òî òî÷êà îêàæåòñÿ â çàêðûòîì

ïàðàëëåëåïèïåäå a

i

<x

i

<b

i

(i=1,2,...,n), îïðåäåëÿåòñÿ ôîðìóëîé [8]

p(a

1

<x

1

<b

1

, a

2

<x

2

<b

2

, ..., a

n

<x

n

<b

n

)

( )

= - + - + +-

= £<£ £<<£

å å å

Fbb b p p p Fbb b

n i

i

n

ij

ijn

ijk

ijkn

n

n1 2

1 1 1

1 2

1,,..., ... ,,..., , (2.101)

ãäå p

i

= F(b

1

,b

2

,...,b

i–1

,a

i

,b

i+1

,...,b

n

), p

ij

= F(b

1

,b

2

,...,b

i–1

,a

i

,b

i+1

,...,b

j–1

,a

j

,b

j+1

,...,b

n

) è ò.ä.

Â ÷àñòíîñòè, äëÿ äâóìåðíîãî ñëó÷àéíîãî âåêòîðà

p(a

1

<x

1

<b

1

,a

2

<x

2

<b

2

) = F(b

1

,b

2

) - F(a

1

,b

2

) - F(b

1

,a

2

) + F(a

1

,a

2

). (2.102)

Ôóíêöèè ðàñïðåäåëåíèÿ (2.100) îáëàäàþò òåìè æå îñíîâíûìè ñâîéñòâàìè, ÷òî è

îäíîìåðíûå ôóíêöèè ðàñïðåäåëåíèÿ:

F(-¥,–¥,...,–¥) = 0, F(+¥,+¥,...,+¥) = 0, 0 £ F(x

1

,x

2

,...,x

n

) £ 1. (2.103)

Ôóíêöèè ðàñïðåäåëåíèÿ ëþáîé èç îäíîìåðíûõ èëè n

1

-ìåðíûõ (n

1

<n) ñîñòàâëÿþùèõ

n-ìåðíîãî âåêòîðà (ò.å. ôóíêöèè ñîâìåñòíîãî ðàñïðåäåëåíèÿ n

1

ñëó÷àéíûõ âåëè÷èí)

ðàâíû ôóíêöèè (2.100) ïîñëå ïîäñòàíîâêè â íåå äëÿ âñåõ ïåðåìåííûõ, íå âõîäÿùèõ â

÷èñëî n

1

, çíà÷åíèé +¥:

F

j

(x

j

) = p(x

ij

<x

j

) = F(+¥,+¥,...,+¥,x

j

,+¥,...,+¥), (2.104)

F

jk

(x

j

,x

k

) = p(x

ij

<x

j

,x

ik

<x

k

) = F(+¥,+¥,...,+¥,x

j

,+¥,...,+¥,x

k

,+¥,...,+¥) (2.105)

è ò.ä. äî n

1

ñëó÷àéíûõ âåëè÷èí â ëþáîì ñî÷åòàíèè. Ôóíêöèè (2.104) è (2.105) íàçûâà-

þòñÿ, ñîîòâåòñòâåííî, îäíî- è äâóìåðíûìè ãðàíè÷íûìè èëè ìàðãèíàëüíûìè ðàñïðå-

äåëåíèÿìè (â îáùåì ñëó÷àå - n

1

-ìåðíûìè ðàñïðåäåëåíèÿìè).

47

Ôóíêöèÿ ðàñïðåäåëåíèÿ äëÿ äèñêðåòíûõ ñëó÷àéíûõ âåêòîðîâ

( ) ( )

Fxx x px xx x x x

n i n nn

k

x x

n

ik k

1 2 1 11 2 22

1

, ,..., , ,...,= = = =

=

<

å

. (2.106)

Ôóíêöèÿ ðàñïðåäåëåíèÿ äëÿ íåïðåðûâíûõ ñëó÷àéíûõ âåêòîðîâ

( ) ( )

Fxx x fxx xdxdx dx

n n n

xxx

n

1 2 1 2 1 2

21

,,..., ... ,,..., ...=

-¥-¥-¥

òòò

, (2.107)

ãäå f(x

1

,x

2

,...,x

n

) - ïëîòíîñòü ðàñïðåäåëåíèÿ ñëó÷àéíîãî âåêòîðà (x

1

,x

2

,...,x

n

) (èëè ñî-

âìåñòíàÿ ïëîòíîñòü ñëó÷àéíûõ âåëè÷èí x

1

,x

2

,...,x

n

):

( )

(

)

( )

fxx x

Fxx x

xx x

fxx xdxdx dx

n

n n1 2

1 2

1 2 1 2

1, ,...,

, ,...,

...

... , ,..., ...= =

-¥

+¥

-¥

+¥

-¥

+¥

òòò

¶

¶ ¶ ¶

,

. (2.108)

Ñîîòâåòñòâåííî ïëîòíîñòè ãðàíè÷íûõ ðàñïðåäåëåíèé (2.104) èëè (2.105)

( )

(

)

( )

fx

Fx

x

fxx xdxdx dx dx dx

j j

j

n j j n

=

- +

-¥

+¥

-¥

+¥

-¥

+¥

òòò

¶

= ... , ,..., ... ...

1 2 1 2 1 1

. (2.109)

( )

(

)

( )

fxx

Fxx

xx

fxx xdxdx dxdx dx dx dx

jk j k

j k

n j j k k n

,

... , ,..., ... ... ...=

- + - +

-¥

+¥

-¥

+¥

-¥

+¥

òòò

¶

¶ ¶

2

1 2 1 2 1 1 1 1

=

. (2.110)

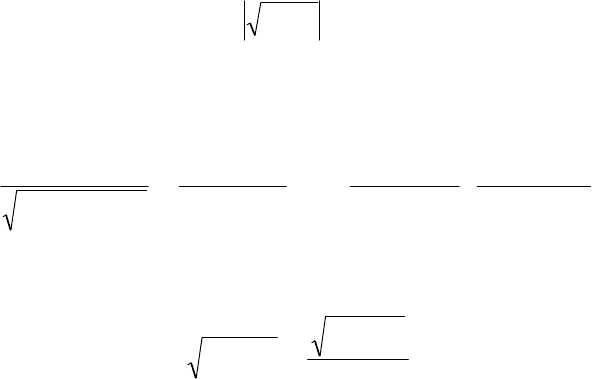
Íàïðèìåð, äëÿ äâóìåðíîãî íîðìàëüíîãî ðàñïðåäåëåíèÿ (ðèñ.2.8) [8]:

( )

( ) ( )( ) ( )

fxx

x x x x

1 2

12

2

1 1

2

1

2

1 1 2 2

12

2 2

2

1

2 1

1

21

2, exp=

-

- -

+

-

é

ë

ê

ù

û

ú

ì

í

ï

î

ï

ü

ý

ï

þ

ï

pss r

r

m

s

r

m m

ss

m

s

, (2.111)

ãäå m

1

= M(x

1

) è m

2

= M(x

2

) - ìàòåìàòè÷åñêèå îæèäàíèÿ, s

1

è s

2

- ñðåäíèå êâàäðàòè÷å-

ñêèå îòêëîíåíèÿ, cov(x

1

,x

2

)= M[(x

1

-m

1

)-(x

2

-m

2

)] - êîâàðèàöèÿ (êîððåëÿöèîííûé ìî-

ìåíò) (2.112), r = cov(x

1

,x

2

)/(s

1

s

2

) - êîýôôèöèåíò êîððåëÿöèè (2.117).

Ïåðâûå íà÷àëüíûå ìîìåíòû ñëó÷àéíîãî âåêòîðà (x

1

,x

2

,...,x

n

) (öåíò-

ðàëüíûå ìîìåíòû ïåðâîãî ïîðÿäêà) êàê è äëÿ îäíîìåðíîãî ñëó÷àÿ ÿâëÿþò-

ñÿ ìàòåìàòè÷åñêèìè îæèäàíèÿìè ñëó÷àéíûõ âåëè÷èí x

1

,x

2

,...,x

n

. Äëÿ íå-

ïðåðûâíîãî âåêòîðà

f

(

x

1

,

x

2

)

x

2

x

1

Ðèñ.2.8. Ïîâåðõíîñòü ïëîòíîñòè äâóìåðíîãî íîðìàëüíîãî ðà

ñ

ïðåäåëåíèÿ

48

( ) ( ) ( )

Mx Mx xfxx xdxdx dx

i i i i n n

= =

-¥

+¥

-¥

+¥

-¥

+¥

òòò

... , ,..., ...

1 2 1 2

. (2.112)

Çíà÷åíèÿ n ìàòåìàòè÷åñêèõ îæèäàíèé M

i

(x

i

) îáðàçóþò â n-ìåðíîì ïðî-

ñòðàíñòâå òî÷êó - öåíòð ðàñïðåäåëåíèÿ âåðîÿòíîñòåé.

Â îáùåì ñëó÷àå âåëè÷èíû M(x

1

r1

x

2

r2

...x

n

rn

) íàçûâàþòñÿ íà÷àëüíûìè

ìîìåíòàìè ïîðÿäêà r

1

+r

2

+...+r

n

. Â ÷àñòíîñòè âòîðûå íà÷àëüíûå ìîìåíòû

(íà÷àëüíûå ìîìåíòû âòîðîãî ïîðÿäêà) ÿâëÿþòñÿ ìàòåìàòè÷åñêèìè îæèäà-

íèÿìè ïðîèçâåäåíèé ñëó÷àéíûõ âåëè÷èí

( ) ( )

( )

Mxx Mxx xxfxx xdxdx dx

ij i j ij ij n n

, ... , ,..., ...= =

-¥

+¥

-¥

+¥

-¥

+¥

òòò

1 2 1 2

. (2.113)

Âåëè÷èíû M{[x

1

-M(x

1

)]

r1

[x

2

-M(x

2

)]

r2

...[x

n

-M(x

n

)]

rn

} íàçûâàþòñÿ öåí-

òðàëüíûìè ìîìåíòàìè ïîðÿäêà r

1

+r

2

+...+r

n

. Âòîðûå öåíòðàëüíûå ìîìåí-

òû (öåíòðàëüíûå ìîìåíòû âòîðîãî ïîðÿäêà) M{[x

i

-M(x

i

)][x

j

-M(x

j

)]} ïðè i¹j

íàçûâàþòñÿ êîâàðèàöèÿìè (êîâàðèàöèîííûìè ìîìåíòàìè) âåëè÷èí x

i

è

x

j

, à ïðè i=j - äèñïåðñèÿìè âåëè÷èí x

i

:

( ) ( )

( )

[ ]

( )

[ ]

( )

Dxx xx x Mx x Mx fxx xdxdx dx

ij i j i j i i j j n n

, cov , ... , ..., ...= = - × - × =

-¥

+¥

-¥

+¥

-¥

+¥

òòò

1 2 1 2

= M{[x

i

- M(x

i

)]×M{[x

j

- M(x

j

)] = M(x

i

x

j

) - M(x

i

)M(x

j

). (2.114)

( ) ( ) ( )

[ ]

( ) ( )

[ ]

{

}

( )

Dxx Dx xMx fx xdxdx MxMx Mx Mx

ii i i i i i n n i i i i

, ... ,..., ...= = - × = - = -

-¥

+¥

-¥

+¥

òò

2

1 1

2

2 2

. (2.115)

Î÷åâèäíî cov(x

i

,x

j

)=cov(x

j

,x

i

).

Ñîîòâåòñòâåííî ñðåäíåå êâàäðàòè÷åñêîå îòêëîíåíèå ñëó÷àéíîé âåëè÷èíû x

i

( )

s .

i i

Dx=

(2.116)

Öåíòðàëüíûå ìîìåíòû âòîðîãî ïîðÿäêà (2.114) è (2.115), ò.å. êîâàðèàöèè è äèñïåð-

ñèè, îïðåäåëÿþò ìàòðèöó ìîìåíòîâ [D

ij

], îïðåäåëèòåëü êîòîðîé det[D

ij

] íàçûâàåòñÿ

îáîáùåííîé äèñïåðñèåé n-ìåðíîãî ðàñïðåäåëåíèÿ.

Äëÿ ñëó÷àéíîãî âåêòîðà (x

1

,x

2

,...,x

n

) ïàðàìåòð

(

)

( )

(

)

( )

(

)

r

ss s s

ij

i j

i i

i

j j

j

xx

Dx Dx

xx

M

x Mx

=

×

= =

-

×

-

é

ë

ê

ù

û

ú

cov , cov ,

(2.117)

íàçûâàåòñÿ êîýôôèöèåíòîì êîððåëÿöèè ìåæäó ñëó÷àéíûìè âåëè÷èíàìè x

i

è x

j

. Êî-

ýôôèöèåíò êîððåëÿöèè ìîæåò ïðèíèìàòü çíà÷åíèÿ ìåæäó -1 è +1. Î÷åâèäíî r

ij

=r

ji

.

Êîýôôèöèåíòû êîððåëÿöèè (2.117) îáðàçóþò êîððåëÿöèîííóþ ìàòðèöó [r

ij

]. Âåëè÷èíà

[ ]

[

]

R

D

ij

n

= =det

det

...

r

ss s

12

(2.118)

íàçûâàåòñÿ êîýôôèöèåíòîì ðàçáðîñà.

Ñëó÷àéíûå âåëè÷èíû x

i

è x

j

íàçûâàþòñÿ íåêîððåëèðîâàííûìè, åñëè èõ êîýôôèöè-

åíò êîððåëÿöèè r

ij

è, ñîîòâåòñòâåííî, êîâàðèàöèÿ cov(x

i

,x

j

) ðàâíû íóëþ (â ïðîòèâíîì

ñëó÷àå - êîððåëèðîâàííûìè). Èç íåçàâèñèìîñòè äâóõ âåëè÷èí ñëåäóåò èõ íåêîððåëèðî-

âàííîñòü, íî èç íåêîððåëèðîâàííîñòè íå îáÿçàòåëüíî ñëåäóåò èõ íåçàâèñèìîñòü, îäíàêî

íåêîððåëèðîâàííûå íîðìàëüíî ðàñïðåäåëåííûå âåëè÷èíû íåçàâèñèìû [9].

Äëÿ íåçàâèñèìûõ äðóã îò äðóãà ñëó÷àéíûõ âåëè÷èí x

i

, î÷åâèäíî,

( ) ( )

px xx x x x px x

i i in n ik k

k

n

1 1 2 2

1

< < < = <

=

Õ

, ,..., , (2.119)

49

ïîýòîìó åñëè ñëó÷àéíûå âåëè÷èíû x

1

, x

2

, ..., x

n

íåçàâèñèìû, òî ôóíêöèÿ

ðàñïðåäåëåíèÿ (2.100) ìîæåò áûòü ïðåäñòàâëåíà â âèäå

( ) ( )

Fxx x Fx

n k

k

n

k1 2

1

, ,..., =

=

Õ

, (2.120)

ãäå F

k

(x

k

) - ôóíêöèÿ ðàñïðåäåëåíèÿ âåëè÷èíû x

k

(îäíîìåðíîå ãðàíè÷íîå ðàñïðåäåëåíèå

(2.104)).

Äëÿ íåçàâèñèìûõ ñëó÷àéíûõ âåëè÷èí ñïðàâåäëèâû ñëåäóþùèå ñîîòíîøåíèÿ:

( ) ( ) ( ) ( )

fxx x fx M x Mx D x Dx

n k

k

n

k k

k

n

k

n

k k

k

n

k

n

1 2

1 1 1

1 1

, ,..., =

æ

è

ç

ö

ø

÷

=

æ

è

ç

ö

ø

÷

=

= = =

= =

Õ Õ Õ

å å

, ,

. (2.121)

Åñëè, íàïðèìåð, íåçàâèñèìûå ñëó÷àéíûå âåëè÷èíû x

1

è x

2

ðàñïðåäåëåíû ïî íîð-

ìàëüíîìó çàêîíó (2.75) ñ ìàòåìàòè÷åñêèìè îæèäàíèÿìè m

1

è m

2

è ñðåäíèìè êâàäðàòè-

÷åñêèìè îòêëîíåíèÿìè s

1

è s

2

, òî ïëîòíîñòü ðàñïðåäåëåíèÿ âåêòîðà (x

1

,x

2

)

( ) ( )( )

( ) ( )

fxx fxfx

x x

1 2 112 2

1

1 1

2

1

2

2 2

2

1

2

1

2

, exp exp= = -

-

é

ë

ê

ù

û

ú

× -

-

é

ë

ê

ù

û

ú

=

s p

m

s

s p

m

s

( ) ( )

= -

-

é

ë

ê

ù

û

ú

1

2

2 2

12

1 1

2

1

2

2 2

2

pss

m

s

m

s

exp

x x

. (2.122)

Óñëîâíûì ðàñïðåäåëåíèåì íàçûâàåòñÿ ðàñïðåäåëåíèå îäíîé èëè íå-

ñêîëüêèõ n

1

ñëó÷àéíûõ âåëè÷èí (n

1

<n) ïðè óñëîâèè, ÷òî âñå îñòàëüíûå

ñëó÷àéíûå âåëè÷èíû ïðèíèìàþò îïðåäåëåííûå çíà÷åíèÿ.

Íàïðèìåð:

F

1/23...n

(x

1

/x

2

,x

3

,...,x

n

) = p(x

i1

<x

1

/x

i2

=x

2

,x

i3

=x

3

,...,x

in

=x

n

), (2.123)

F

12/34...n

(x

1

,x

2

/x

3

,x

4

,...,x

n

) = p(x

i1

<x

1

,x

i2

<x

2

/x

i3

=x

3

,x

i4

=x

4

,...,x

in

=x

n

). (2.124)

Ïëîòíîñòè óñëîâíûõ è ãðàíè÷íûõ (ìàðãèíàëüíûõ) ðàñïðåäåëåíèé ñâÿçàíû äðóã ñ

äðóãîì ñîîòíîøåíèÿìè âèäà

( )

(

)

( )

(

)

( )

(

)

( )

f x x

fxx

fx

f x xx

f xxx

fxx

f xx x

f xxx

fx

12

1 2

12 1 2

2 2

123

1 2 3

123 1 2 3

23 2 3

123

1 2 3

123 1 2 3

3 3

/ / /

/

,

/,

,,

,

,/

,,

= = =, ,

. (2.125)

Äëÿ óñëîâíûõ ðàñïðåäåëåíèé ìîãóò áûòü îïðåäåëåíû óñëîâíûå ìàòåìà-

òè÷åñêèå îæèäàíèÿ è äèñïåðñèè.

2.2.7. Функции от случайных величин

Åñëè ñëó÷àéíûå âåëè÷èíû x è y ñâÿçàíû äðóã ñ äðóãîì ñîîòíîøåíèåì

y=y(x) è èçâåñòíû ôóíêöèè ðàñïðåäåëåíèÿ F

x

(x) è f

x

(x), òî ôóíêöèè ðàñ-

ïðåäåëåíèÿ

( ) ( )

[ ]

( ) ( )

[ ]

Fy Fxy fy fxy

dx

dy

y x y x

= , = × . (2.126)

Â îáùåì ñëó÷àå, åñëè ñëó÷àéíûå âåêòîðû (x

1

,x

2

,...,x

n

) è (y

1

,y

2

,...,y

n

)

ñâÿçàíû äðóã ñ äðóãîì ñîîòíîøåíèåì y

i

= y

i

(x

1

,x

2

,...,x

n

), òî èõ ïëîòíîñòè

ðàñïðåäåëåíèÿ f

x

(x

1

,x

2

,...,x

n

) è f

y

(x

1

,x

2

,...,x

n

) ñâÿçàíû ñîîòíîøåíèåì

( ) ( )

(

)

( )

fyy y fxx x

yy y

xx x

y n x n

n

1 2 1 2

1 2

, ,..., , ,...,

, ,...,

=

¶

. (2.127)

Ìàòåìàòè÷åñêîå îæèäàíèå ñëîæíîé ôóíêöèè j[y(x)]

( )

[ ]

( )

[ ]

{ }

( )

[ ]

( )

M y M yx yxdFx

x

j j j= =

-¥

+¥

ò

. (2.128)

50

Â îáùåì ñëó÷àå, åñëè y

i

= y

i

(x

1

,x

2

,...,x

n

), òî ìàòåìàòè÷åñêîå îæèäàíèå

ôóíêöèè j(y

1

,y

2

,...,y

m

)

( )

[ ]

( )

M yy y dFxx x

m x n

j j

1 2 1 2

, ,..., ... , ,...,=

-¥

+¥

-¥

+¥

-¥

+¥

òòò

. (2.129)

Äëÿ ëèíåéíîé ôóíêöèè y = ax + b

( ) ( ) ( ) ( ) ( ) ( ) ( )

fy

a

f

yb

a

My Maxb aMx bDy Daxb aDx

y x

=

-

æ

è

ç

ö

ø

÷

= + = + = + =

1

2

, ,

. (2.130)

Â áîëåå îáùåì ñëó÷àå

( )

Ma ax a aMx Da ax a a

ii

i

n

i i

i

n

ii

i

n

ii j

j

n

jij

i

n

0

1

0

1

0

1 11

+

æ

è

ç

ö

ø

÷

= + +

æ

è

ç

ö

ø

÷

=

= = = ==

å å å åå

, s sr

. (2.131)

Åñëè â îêðåñòíîñòÿõ òî÷êè x

0

ôóíêöèþ y(x) ìîæíî ïðèáëèæåííî ïðåä-

ñòàâèòü â âèäå ëèíåéíîé çàâèñèìîñòè y » y(x

0

)+y¢(x

0

)(x–x

0

), òî ìàòåìàòè-

÷åñêîå îæèäàíèå è äèñïåðñèÿ

M[y(x)] » y(x

0

), D[y(x)] » [y¢(x

0

)]

2

D(x). (2.132)

Åñëè èçâåñòíà ôóíêöèÿ ñîâìåñòíîãî ðàñïðåäåëåíèÿ äâóõ ñëó÷àéíûõ âå-

ëè÷èí f(x,y), òî ôóíêöèÿ ðàñïðåäåëåíèÿ ñóììû ýòèõ âåëè÷èí z = x + y

() ( )

fz fxz xdx= -

-¥

+¥

ò

, . (2.133)

Ñîîòâåòñòâåííî, ìàòåìàòè÷åñêîå îæèäàíèå è äèñïåðñèÿ

M(z)=M(x

1

)+M(x

2

), D(z)=D(x

1

)+D(x

2

)+2cov(x

1

,x

2

)=s

1

2

+s

2

+2r

12

s

1

s

2

. (2.134)

Äëÿ íåçàâèñèìûõ ñëó÷àéíûõ âåëè÷èí f(x,y) = f

1

(x)f

2

(y) è

() () ( )

fz fxfz xdx= -

-¥

+¥

ò

1 2

. (2.135)

Ðàñïðåäåëåíèå ñóììû n âçàèìíî íåçàâèñèìûõ ñëó÷àéíûõ âåëè÷èí x

i

,

ðàñïðåäåëåíèÿ êîòîðûõ ñèììåòðè÷íû îòíîñèòåëüíî ìàòåìàòè÷åñêèõ îæè-

äàíèé, ìîæíî àïïðîêñèìèðîâàòü íîðìàëüíûì ðàñïðåäåëåíèåì äàæå ïðè

íåáîëüøèõ çíà÷åíèÿõ n [10].

Ðàñïðåäåëåíèå ñóììû äâóõ íåçàâèñèìûõ ìíîãîìåðíûõ ñëó÷àéíûõ âåëè-

÷èí (x

1

,x

2

,...,x

n

) è (y

1

,y

2

,...,y

n

) ïðè z

i

=x

i

+y

i

( ) ( ) ( )

Fzz z Fz xz x z xdFxx x

z n y n n x n1 2 1 1 2 2 1 2

,,..., ... , ,..., , ,...,= - - -

-¥

+¥

-¥

+¥

-¥

+¥

òòò

. (2.136)

Ôóíêöèÿ ðàñïðåäåëåíèÿ ïðîèçâåäåíèÿ ñëó÷àéíûõ âåëè÷èí z = x×y

()

fz fx

z

xx

dx=

æ

è

ç

ö

ø

÷

-¥

+¥

ò

,

1

. (2.137)

Ôóíêöèÿ ðàñïðåäåëåíèÿ îòíîøåíèÿ ñëó÷àéíûõ âåëè÷èí z = x/y

() ( ) ( )

fz xfzxxdx xfzxxdx= -

+¥

-¥

ò ò

, ,

0

. (2.138)

Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1

Подождите немного. Документ загружается.