Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1
Подождите немного. Документ загружается.


51
2.2.8. Регрессионные зависимости
Ñëó÷àéíûå âåëè÷èíû, çàâèñÿùèå îò îäíèõ è òåõ æå ñëó÷àéíûõ ôàêòî-
ðîâ, íàçûâàþòñÿ ñòîõàñòè÷åñêè (èëè ñòàòèñòè÷åñêè) çàâèñèìûìè. Íà-
ïðèìåð, åñëè ñëó÷àéíûå âåëè÷èíû x è y çàâèñÿò îò ñëó÷àéíûõ ôàêòîðîâ z
i
x = x(z
1
,z
2
,...,z
n
), y = y(z
1
,z
2
,...,z
m
), (2.139)
òî îíè ñòîõàñòè÷åñêè çàâèñèìû.  îáùåì ñëó÷àå, åñëè n¹m, òî ñðåäè ñëó-
÷àéíûõ ôàêòîðîâ z
i
åñòü òàêèå, êîòîðûå âëèÿþò íà îäíó èç âåëè÷èí x è y.
Ðåãðåññèåé íàçûâàåòñÿ ëþáàÿ ôóíêöèÿ g(x), ïðèáëèæåííî ïðåäñòàâ-
ëÿþùàÿ ñòîõàñòè÷åñêóþ çàâèñèìîñòü îäíîé ñëó÷àéíîé âåëè÷èíû y îò äðó-
ãîé x. Ñëó÷àéíàÿ âåëè÷èíà y ïðåäñòàâëÿåòñÿ êàê ñóììà äâóõ ñëó÷àéíûõ
âåëè÷èí
y = g(x) + h(x,y), (2.140)
ïðè ýòîì ñëó÷àéíàÿ âåëè÷èíà h(x,y) ðàññìàòðèâàåòñÿ â êà÷åñòâå ïîïðà-
âî÷íîãî ÷ëåíà (îñòàòêà).
Ñðåäíÿÿ êâàäðàòè÷åñêàÿ ðåãðåññèÿ
( )
( ) ( )
gx My x yf y xdy
yx
= =
-¥
+¥
ò
/ /
/
(2.141)
ìèíèìèçèðóåò ñðåäíèé êâàäðàò îòêëîíåíèÿ g(x) îò y (ò.å. ìèíèìèçèðóåò
ñðåäíåå çíà÷åíèå êâàäðàòà îñòàòêà h(x,y)):
M{[y
-
g(x)]
2
} = M[h
2
(x,y)]. (2.142)
Ñîîòâåòñòâóþùàÿ êðèâàÿ y = M(y/x) íàçûâàåòñÿ êðèâîé ñðåäíåé êâàäðà-
òè÷åñêîé ðåãðåññèè.
×àñòî îêàçûâàåòñÿ äîñòàòî÷íûì àïïðîêñèìèðîâàòü ðåãðåññèþ (2.141)
ëèíåéíîé ôóíêöèåé (ëèíåéíîé ðåãðåññèåé) âèäà
g(x) = M(y) + b
yx
[x - M(x)] = m
y
+ b
yx
(x – m
x
), (2.143)
ãäå m
x
è m
y
- ìàòåìàòè÷åñêèå îæèäàíèÿ, b
yx
- òåîðåòè÷åñêèé êîýôôèöèåíò ðåãðåññèè.
Äëÿ òîãî ÷òîáû ìèíèìèçèðîâàòü ñðåäíèé êâàäðàò îòêëîíåíèÿ (2.142), â
âûðàæåíèè (2.143) êîýôôèöèåíò ðåãðåññèè b
yx
ðàññ÷èòûâàåòñÿ ïî ôîðìóëå
(
)
(
)
b r
s
s ss
s
s
s
yx yx
y
x xy
y
x
x
xy xy
= = × =
cov, cov,
2
, (2.144)
ãäå r
yx
è cov(x,y) - êîýôôèöèåíò êîððåëÿöèè è êîâàðèàöèÿ ñëó÷àéíûõ âåëè÷èí x è y
(ñì.ðàçä.2.2.6), s
x
è s
y
- ñðåäíèå êâàäðàòè÷åñêèå îòêëîíåíèÿ ñëó÷àéíûõ âåëè÷èí x è y.
Ïðè îïðåäåëåíèè êîýôôèöèåíòà ðåãðåññèè ïî ôîðìóëå (2.144) ñðåäíèé
êâàäðàò îòêëîíåíèÿ (2.142) (îñòàòî÷íàÿ äèñïåðñèÿ) ðàâåí s
y
2
(1–r
yx
2
),
ïîýòîìó êîýôôèöèåíò êîððåëÿöèè r
yx
ìîæåò ñëóæèòü ìåðîé êà÷åñòâà ëè-
íåéíîé àïïðîêñèìàöèè (2.143).
Ðåãðåññèÿ (2.141) ìîæåò áûòü áîëåå òî÷íî àïïðîêñèìèðîâàíà ìíîãî-
÷ëåíàìè áîëåå âûñîêèõ ñòåïåíåé èëè äðóãèìè ôóíêöèÿìè, îäíàêî ëèíåé-
íàÿ ðåãðåññèÿ (2.143) èñïîëüçóåòñÿ ÷àùå âñåãî.
 áîëåå îáùåì ñëó÷àå, åñëè èçâåñòíî ñîâìåñòíîå ðàñïðåäåëåíèå n ñëó-
÷àéíûõ âåëè÷èí (x
1
,x
2
,...,x
n
) âèäà (2.100), òî çàâèñèìîñòü ëþáîé èç ýòèõ
âåëè÷èí (íàïðèìåð, x
1
) ìîæåò áûòü âûðàæåíà ÷åðåç îñòàëüíûå n–1 âåëè-
÷èí ôîðìóëîé âèäà (2.140)

52
x
1
= g
1
(x
2
,x
3
,...,x
n
) + h
1
(x
1
,x
2
,...,x
n
), (2.145)
ïðè÷åì ñðåäíèé êâàäðàò îòêëîíåíèÿ
M{[x
1
-
g(x
2
,x
3
,...,x
n
)]
2
} = M[h
1
2
(x
1
,x
2
,...,x
n
)] (2.146)
ìèíèìèçèðóåòñÿ ñðåäíåé êâàäðàòè÷åñêîé ðåãðåññèåé âèäà (2.141):
( )
( ) ( )
gxx x Mx xx x xf x xx xdx
n n
n
n1 2 3 1 2 3 1
123
1 2 3 1
, ,..., / , ,..., / , ,...,
/...
= =
-¥
+¥
ò
, (2.147)
ãäå M(x
1
/x
2
,x
3
,...,x
n
) è f
1/23...n
(x
1
/x
2
,x
3
,...,x
n
) - óñëîâíîå ìàòåìàòè÷åñêîå îæèäàíèå
(ñðåäíåå çíà÷åíèå) è ïëîòíîñòü óñëîâíîãî ðàñïðåäåëåíèÿ âåëè÷èíû x
1
(ñì.ðàçä.2.2.6).
Ëèíåéíàÿ ðåãðåññèÿ îäíîìåðíîé ñëó÷àéíîé âåëè÷èíû x
i
îòíîñèòåëüíî
îñòàëüíûõ n-1 îäíîìåðíûõ ñëó÷àéíûõ âåëè÷èí
( ) ( )
[ ]
( )
g Mx x Mx x
i i ik k k
k
n
i ik k k
k
n
ik
ik
ii
ki ki
= + - = + - =-
= =
¹ ¹
å å
b m b m b
1 1
,
L
L
, (2.148)
ãäå [L
ik
] = [D
ik
]
-
1
- ìàòðèöà, îáðàòíàÿ ìàòðèöå ìîìåíòîâ (ñì.ðàçä.2.2.6).
Ìåðîé êîððåëÿöèè ìåæäó x
i
è îñòàëüíûìè n–1 ñëó÷àéíûìè âåëè÷èíà-
ìè ÿâëÿåòñÿ ñâîäíûé êîýôôèöèåíò êîððåëÿöèè
( )
( )
r xg
Dx
i i
i i ii
, = -1
1
L
. (2.149)
Ïðèâåäåííûå ôîðìóëû (2.139)-(2.149) ÿâëÿþòñÿ òåîðåòè÷åñêîé îñíîâîé
äëÿ îïðåäåëåíèÿ ýìïèðè÷åñêèõ çàâèñèìîñòåé ñëó÷àéíûõ âåëè÷èí è ïî-
ñòðîåíèÿ ýìïèðè÷åñêèõ óðàâíåíèé ðåãðåññèé.
2.3. Элементы теории случайных функций и процессов
 òåîðèè íàäåæíîñòè íàðÿäó ñ îäíîìåðíûìè è ìíîãîìåðíûìè ñëó÷àé-
íûìè âåëè÷èíàìè ðàññìàòðèâàþòñÿ ñëó÷àéíûå ôóíêöèè, ò.å. ôóíêöèè, êî-
òîðûå ìîãóò ñëó÷àéíûì îáðàçîì ïðèíèìàòü òîò èëè èíîé êîíêðåòíûé âèä
â çàâèñèìîñòè îò çíà÷åíèÿ àðãóìåíòà.
2.3.1. Основные понятия и определения [3,11,12]
Ñëó÷àéíîé ôóíêöèåé íàçûâàåòñÿ ôóíêöèÿ X(t), çíà÷åíèÿ êîòîðîé ïðè
ëþáîì çíà÷åíèè íåñëó÷àéíîãî àðãóìåíòà t ÿâëÿþòñÿ ñëó÷àéíûìè âåëè÷è-
íàìè ñ îïðåäåëåííûì ðàñïðåäåëåíèåì âåðîÿòíîñòåé.
Àðãóìåíòàìè ñëó÷àéíîé ôóíêöèè ìîãóò áûòü âðåìÿ, êîîðäèíàòà è äðó-
ãèå íåñëó÷àéíûå ïàðàìåòðû.  îáùåì ñëó÷àå àðãóìåíòîâ ìîæåò áûòü íå-
ñêîëüêî, îäíàêî ÷àùå âñåãî åäèíñòâåííûì àðãóìåíòîì ÿâëÿåòñÿ âðåìÿ èëè
äðóãîé ïàðàìåòð, êîòîðûé ìîæåò áûòü èíòåðïðåòèðîâàí êàê âðåìÿ. Òàêèå
ñëó÷àéíûå ôóíêöèè íàçûâàþòñÿ ñëó÷àéíûìè ïðîöåññàìè.
Äëÿ ñëó÷àéíûõ ïðîöåññîâ îïðåäåëÿåòñÿ âåðîÿòíîñòü èõ òå÷åíèÿ (íàïðè-
ìåð, èçìåíåíèå êîîðäèíàò ÷àñòèö, ñîâåðøàþùèõ áðîóíîâñêîå äâèæåíèå,
òóðáóëåíòíîå òå÷åíèå æèäêîñòåé è ãàçîâ, ðàñïðîñòðàíåíèå ðàäèîâîëí ïðè
íàëè÷èè ïîìåõ, òðàíñïîðòíûå ïîòîêè è äð.). Ñëó÷àéíûìè ïðîöåññàìè
ìîæíî òàêæå ñ÷èòàòü ñëó÷àéíûå âåëè÷èíû, êîòîðûå ÿâëÿþòñÿ ñëó÷àéíûìè
ôóíêöèÿìè îäíîãî èëè íåñêîëüêèõ ïàðàìåòðîâ, ïðè÷åì ýòè ïàðàìåòðû ìî-
ãóò èçìåíÿòüñÿ íåïðåðûâíî èëè ïðèíèìàòü òîëüêî äèñêðåòíûå çíà÷åíèÿ.
53
 òåîðèè íàäåæíîñòè ñëó÷àéíûì ïðîöåññîì ÿâëÿåòñÿ, â ÷àñòíîñòè, èç-
ìåíåíèå ñîñòîÿíèå ñèñòåìû, ÿâëÿþùååñÿ ôóíêöèåé âðåìåíè èëè íàðàáîò-
êè. Ðàçíîâèäíîñòüþ ñëó÷àéíûõ ïðîöåññîâ ÿâëÿåòñÿ òàêæå âîçíèêíîâåíèå
îòêàçîâ ýëåìåíòà èëè ñèñòåìû.
Ñëó÷àéíûé (âåðîÿòíîñòíûé, ñòîõàñòè÷åñêèé) ïðîöåññ - ïðîöåññ èçìå-
íåíèÿ âî âðåìåíè ñîñòîÿíèÿ ñèñòåìû â ñîîòâåòñòâèè ñ âåðîÿòíîñòíûìè
çàêîíîìåðíîñòÿìè. Õàðàêòåðèñòèêè ñëó÷àéíîãî ïðîöåññà â ëþáîé ìîìåíò
âðåìåíè - ñëó÷àéíûå âåëè÷èíû ñ îïðåäåëåííûì ðàñïðåäåëåíèåì.
Ñëó÷àéíûé ïðîöåññ îáû÷íî ïðåäñòàâëÿåòñÿ êàê îäíîïàðàìåòðè÷åñêîå
ñåìåéñòâî ñëó÷àéíûõ âåëè÷èí X(t). Ïàðàìåòð t â îáùåì ñëó÷àå ïðèíèìàåò
ïðîèçâîëüíûå äåéñòâèòåëüíûå çíà÷åíèÿ è îáû÷íî ÿâëÿåòñÿ âðåìåíåì (åñëè
ïàðàìåòð t - âåêòîð, ò.å. ïðîöåññ çàâèñèò îò íåñêîëüêèõ àðãóìåíòîâ, òî ñå-
ìåéñòâî ñëó÷àéíûõ âåëè÷èí X(t) íàçûâàåòñÿ ñëó÷àéíûì ïîëåì). Êàê ïðà-
âèëî, X(t) - ÷èñëîâàÿ ôóíêöèÿ âðåìåíè. Åñëè çíà÷åíèÿ X(t) ÿâëÿþòñÿ âåê-
òîðàìè, òî ñëó÷àéíûé ïðîöåññ íàçûâàåòñÿ ìíîãîìåðíûì.
Âîçìîæíûå çíà÷åíèÿ X(t) îïðåäåëÿþò ñîñòîÿíèÿ ñèñòåìû (ñîñòîÿíèÿ
ñëó÷àéíîãî ïðîöåññà) â ëþáîé ìîìåíò âðåìåíè è ìîãóò áûòü ñõåìàòè÷åñêè
ïðåäñòàâëåíû êàê òî÷êè ôàçîâîãî ïðîñòðàíñòâà (ïðîñòðàíñòâà ñîñòîÿíèé).
Ñëó÷àéíûé ïðîöåññ X(t) îáû÷íî îïèñûâàåòñÿ ñîâîêóïíîñòüþ n-ìåðíûõ
ðàñïðåäåëåíèé âåðîÿòíîñòåé âåëè÷èí X(t
1
), X(t
2
), ..., X(t
n
) äëÿ ìîìåíòîâ
âðåìåíè t
1
, t
2
, ..., t
n
ïðè ëþáîì n > 0, êîòîðûå íàçûâàþòñÿ êîíå÷íîìåð-
íûìè ðàñïðåäåëåíèÿìè ñëó÷àéíîãî ïðîöåññà:
F(x
1
,x
2
,...,x
n
; t
1
,t
2
,...,t
n
) = p{X(t
1
)<x
1
,X(t
2
)<x
2
,...,X(t
n
)<x
n
} (2.150)
(â âûðàæåíèè (2.150) X(t
i
) è x
i
äëÿ îïðåäåëåííîñòè â äàëüíåéøåì áóäåì
ñ÷èòàòü ñêàëÿðíûìè âåëè÷èíàìè). Ïðè ýòîì ôóíêöèè
F(x
1
,x
2
,...,x
n
;t
1
,t
2
,...,t
n
) äîëæíû îòâå÷àòü äâóì óñëîâèÿì:
- óñëîâèå ñèììåòðèè: äëÿ ëþáîé ïåðåñòàíîâêè i
1
, i
2
, ..., i
n
äîëæíî âû-
ïîëíÿòüñÿ ðàâåíñòâî
(
)
(
)
Fxx x tt t Fxx xtt t
i i i i i i n n
n n1 2 1 2
1 2 12
, ,..., ;, ,..., , ,..., ;,,...,= ; (2.151)
- óñëîâèå ñîãëàñîâàííîñòè: ïðè m < n è ëþáûõ t
m+1
, t
m+2
, ..., t
n
äîëæíî âûïîëíÿòüñÿ ðàâåíñòâî
F(x
1
,x
2
,...,x
m
,...,+¥; t
1
,t
2
,...,t
m
,...,t
n
) = F(x
1
,x
2
,...,x
m
; t
1
,t
2
,...,t
m
). (2.152)
Ñëó÷àéíûå ïðîöåññû êëàññèôèöèðóþòñÿ, ïðåæäå âñåãî, ïî ñòðîåíèþ
ôàçîâîãî ïðîñòðàíñòâà (äèñêðåòíîå è íåïðåðûâíîå) è ïî õàðàêòåðó èçìå-
íåíèÿ àðãóìåíòà (äèñêðåòíîå è íåïðåðûâíîå âðåìÿ). Ñëó÷àéíûé ïðîöåññ ñ
äèñêðåòíûìè öåëî÷èñëåííûìè çíà÷åíèÿìè âðåìåíè íàçûâàþòñÿ òàêæå
ñëó÷àéíîé ïîñëåäîâàòåëüíîñòüþ èëè âðåìåííûì ðÿäîì.
Ïî õàðàêòåðó çàâèñèìîñòè çíà÷åíèÿìè X(t) ñëó÷àéíûå ïðîöåññû äåëÿò-
ñÿ íà íåñêîëüêî êëàññîâ, îòâå÷àþùèõ ñëåäóþùèì óñëîâèÿì:
- ñëó÷àéíûå ïðîöåññû ñ íåçàâèñèìûìè çíà÷åíèÿìè: ïðè ëþáûõ t
1
è t
2
(t
1
¹ t
2
) âåëè÷èíû X(t
1
) è X(t
2
) íåçàâèñèìû;
- ñëó÷àéíûå ïðîöåññû ñ íåçàâèñèìûìè ïðèðàùåíèÿìè: äëÿ ëþáûõ
íåïåðåñåêàþùèõñÿ èíòåðâàëîâ âðåìåíè [t
1
,t
2
] è [t
3
,t
4
] (t
2
<t
3
) ñëó÷àéíûå
âåëè÷èíû X(t
2
)-X(t
1
) è X(t
4
)-X(t
3
) íåçàâèñèìû;

54
- ìàðêîâñêèå ïðîöåññû (ñëó÷àéíûå ïðîöåññû áåç ïîñëåäåéñòâèÿ): óñ-
ëîâíîå ðàñïðåäåëåíèå X(t
1
) ïðè t
1
>t
0
çàâèñèò òîëüêî îò X(t
0
) (ïðè çàäàí-
íûõ çíà÷åíèÿõ X(t) ïðè t £ t
0
), ò.å. ñîñòîÿíèå ñëó÷àéíîãî ïðîöåññà X(t) â
ëþáîé ìîìåíò âðåìåíè t
0
îïðåäåëÿåò ðàñïðåäåëåíèå âåðîÿòíîñòåé, îòíî-
ñÿùååñÿ ê áóäóùåìó ïðîöåññà;
- ñòàöèîíàðíûå ñëó÷àéíûå ïðîöåññû: âåðîÿòíîñòíûå õàðàêòåðèñòèêè
ñëó÷àéíîãî ïðîöåññà íå çàâèñÿò îò âðåìåíè, â ÷àñòíîñòè ïðè ëþáûõ t è Dt
ñëó÷àéíûå âåëè÷èíû X(t) è X(t+Dt) èìåþò îäèíàêîâîå ðàñïðåäåëåíèå, ñëó-
÷àéíûå âåëè÷èíû (X(t
1
),X(t
2
)) è (X(t
1
+Dt),X(t
2
+Dt)) èìåþò îäèíàêîâûå ñî-
âìåñòíûå ðàñïðåäåëåíèÿ è ò.ä. (ñðåäè ñòàöèîíàðíûõ ïðîöåññîâ îñîáóþ
ðîëü èãðàþò ãàóññîâñêèå ïðîöåññû, ó êîòîðûõ âñå êîíå÷íîìåðíûå ðàñïðå-
äåëåíèÿ âåðîÿòíîñòåé ÿâëÿþòñÿ íîðìàëüíûìè);
- ìàðòèíãàëû: óñëîâíîå ìàòåìàòè÷åñêîå îæèäàíèå X(t) ðàâíî X(t
0
)
(ïðè óñëîâèè, ÷òî èçâåñòíî ïîâåäåíèå ïðîöåññà äî ìîìåíòà t
0
<t).
 òåîðèè íàäåæíîñòè â îñíîâíîì ðàññìàòðèâàþòñÿ ñëó÷àéíûå ïðîöåññû
ìàðêîâñêîãî òèïà, â ïåðâóþ î÷åðåäü - ïðîñòûå îäíîðîäíûå öåïè Ìàðêîâà.
2.3.2. Цепи Маркова [2,12]
Ïðîñòîé öåïüþ Ìàðêîâà íàçûâàåòñÿ ñëó÷àéíàÿ ôóíêöèÿ X(t) ñ äèñ-
êðåòíûì âðåìåíåì t (t
0
, t
1
, ..., t
n
, t
i
³ t
i+1
) è äèñêðåòíûì ìíîæåñòâîì çíà-
÷åíèé x
i
(x
0
, x
1
, ..., x
n
), â êîòîðîé ïðè ëþáûõ äîïóñòèìûõ çíà÷åíèÿõ àðãó-
ìåíòà t çàêîí ðàñïðåäåëåíèÿ îðäèíàòû X(t
i
) ïîëíîñòüþ îïðåäåëÿåòñÿ çíà-
÷åíèåì îðäèíàòû X(t
i
-
1
) è íå çàâèñèò îò çíà÷åíèé îðäèíàò X(t
i
-
2
), X(t
i
-
3
) è
ò.ä. Âåðîÿòíîñòü òîãî, ÷òî åñëè â ìîìåíò t
i
-
1
öåïü Ìàðêîâà X(t) èìåëà
çíà÷åíèå x
j
, òî â ìîìåíò t
i
îíà ïðèìåò çíà÷åíèå x
k
, íàçûâàåòñÿ âåðîÿòíî-
ñòüþ ïåðåõîäà èç ñîñòîÿíèÿ x
j
â ñîñòîÿíèå x
k
:
p[X(t
i
)=x
k
/X(t
i–1
)=x
i
] = p
jk
(t
i–1
,t
i
). (2.153)
Ïðîñòàÿ öåïü Ìàðêîâà íàçûâàåòñÿ îäíîðîäíîé ïî âðåìåíè, åñëè âåðî-
ÿòíîñòü ïåðåõîäà p
jk
(t
i–1
,t
i
) èç ñîñòîÿíèÿ x
j
â ñîñòîÿíèå x
k
çà ïðîìåæóòîê
âðåìåíè t = t
i
-
t
i–1
çàâèñèò îò äëèíû ïðîìåæóòêà t è íå çàâèñèò îò ìîìåí-
òà âðåìåíè t
i
-
1
, ò.å. íå çàâèñèò îò íà÷àëà îòñ÷åòà:
p
jk
(t
i
-
1
,t
i
) = p
jk
(t). (2.154)
Âåðîÿòíîñòè ïåðåõîäîâ èç ñîñòîÿíèÿ â ñîñòîÿíèå çà èíòåðâàë âðåìåíè
t äëÿ âñåé öåïè ìîæíî ñâåñòè â ìàòðèöó ïåðåõîäîâ G(t):
()
Gt=
p p p p
p p p p
p p p p
p p p p
k n
k n
j j jk jn
n n nk nn
00 01 0 0
10 11 1 1
0 1
0 1
... ...
... ...
... ...............
... ...
... ...............
... ...
. (2.155)
Î÷åâèäíî, âñå ýëåìåíòû ìàòðèöû ïåðåõîäîâ íåîòðèöàòåëüíû, ìîãóò
èìåòü çíà÷åíèå îò 0 äî 1 è ñóììà ýëåìåíòîâ ëþáîé ñòðîêè ðàâíà åäèíèöå.

55
Âåêòîð p(t
i
) = [p
0
(t
i
), p
1
(t
i
), ..., p
n
(t
i
)], ãäå p
j
(t
i
) - âåðîÿòíîñòü òîãî, ÷òî
ôóíêöèÿ X(t) â ìîìåíò t
i
ïðèíèìàåò çíà÷åíèå x
j
, íàçûâàåòñÿ âåêòîðîì
âåðîÿòíîñòåé ïðîñòîé öåïè Ìàðêîâà â ìîìåíò t
i
. Î÷åâèäíî, âñå ýëåìåí-
òû âåêòîðà âåðîÿòíîñòåé íåîòðèöàòåëüíû, ìîãóò èìåòü çíà÷åíèå îò 0 äî 1
è ñóììà ýëåìåíòîâ ðàâíà åäèíèöå.
 òåîðèè ñëó÷àéíûõ ôóíêöèé äîêàçûâàåòñÿ, ÷òî âåêòîð âåðîÿòíîñòåé
ñîñòîÿíèé ïðîñòîé öåïè Ìàðêîâà â ìîìåíò t
i
ðàâåí ïðîèçâåäåíèþ âåêòîðà
âåðîÿòíîñòåé ñîñòîÿíèé â ìîìåíò t
i–1
íà ìàòðèöó ïåðåõîäîâ, ò.å.
p(t
i
) = p(t
i
-
1
)×G(t). (2.156)
Íàïðèìåð, äëÿ öåïè c äâóìÿ äîïóñòèìûìè ñîñòîÿíèÿìè x
0
è x
1
äëÿ ìîìåíòîâ âðå-
ìåíè t
0
è t
1
ìîæíî çàïèñàòü
() ( )
()
( ) ( )
[ ]
( ) ( ) ( ) ( )
[ ]
p pt t pt pt
p p
p p
ptp ptp ptp ptp
1 0 00 10
00 01
10 11
00 00 10 10 00 01 10 11
= × = × = + +Gt ; ;
.(2.157)
Ïðèìåíèâ ôîðìóëó (2.156) i ðàç, ìîæíî â èòîãå ïîëó÷èòü
p(t
i
) = p(t
i
-
1
)×G(t) = p(t
i
-
2
)×G
2
(t) = ... = p(t
1
)×G
i
-
1
(t) = p(t
0
)×G
i
(t), (2.158)
ò.å. âåêòîð âåðîÿòíîñòåé p(t
i
) èëè ðàñïðåäåëåíèå îðäèíàòû X(t
i
) äëÿ ëþáî-
ãî ìîìåíòà âðåìåíè t
i
è ïðîñòàÿ îäíîðîäíàÿ öåïü Ìàðêîâà ïîëíîñòüþ îï-
ðåäåëÿþòñÿ âåêòîðîì âåðîÿòíîñòåé p(t
0
) è ìàòðèöåé ïåðåõîäîâ G(t).
 âûðàæåíèè (2.158) G
i
- ìàòðèöà ïåðåõîäîâ p
jk
(it) çà âðåìÿ it ñ òåìè
æå ñâîéñòâàìè, ÷òî è ìàòðèöà G(t): âñå ýëåìåíòû íåîòðèöàòåëüíû, ìîãóò
èìåòü çíà÷åíèÿ îò 0 äî 1, ñóììà ýëåìåíòîâ êàæäîé ñòðîêè ðàâíà åäèíèöå.
Åñòåñòâåííî ïðåäïîëîæèòü, ÷òî äëÿ îäíîðîäíûõ öåïåé Ìàðêîâà ïðè
óâåëè÷åíèè èíòåðâàëà it âëèÿíèå íà÷àëüíîãî ñîñòîÿíèÿ óìåíüøàåòñÿ è
ïðè äîñòàòî÷íî áîëüøîì èíòåðâàëå ñòàíîâèòñÿ íè÷òîæíî ìàëûì, ò.å.
(
)
lim
i
jk k
pi p
®¥
=
t
. (2.159)
Îäíîðîäíàÿ ïðîñòàÿ öåïü Ìàðêîâà, äëÿ ëþáûõ äâóõ ñîñòîÿíèé êîòîðîé
ñïðàâåäëèâî ðàâåíñòâî (2.159), íàçûâàåòñÿ ýðãîäè÷åñêîé.
Äëÿ ýðãîäè÷åñêîé öåïè
( ) ( )
(
)
(
)
(
)
( ) ( ) ( )
( ) ( ) ( )
lim lim lim
...
...
... ... ... ...
...
...
...
............
...
i
i
i i
n
n
n n nn
n
n
n
i i
p i p i p i
p i pi pi
p i pi p i
p p p
p p p
p p p
®¥ ®¥ ®¥
= = =G Gt t
t t t
t t t
t t t
00 01 0
10 11 1
0 1
0 1
0 1
0 1
, (2.160)
ò.å. i-ÿ ñòåïåíü ìàòðèöû ïåðåõîäîâ ïðè i®¥ ñòðåìèòñÿ ê ïðåäåëüíîé ìàò-
ðèöå ñ îäèíàêîâûìè ñòðîêàìè.
Ïåðåõîäÿ ê ïðåäåëàì â ðàâåíñòâå (2.158), ìîæíî ïîëó÷èòü
() ( )
()
[ ]
( )
()
( ) ( ) ( )
[ ]
lim lim lim , ,...,
...
...
............
...
i
i
i
i
i
i
n
n
n
n
t t t pt pt pt
pp p
pp p
pp p
®¥ ®¥ ®¥
= × = × = × =p p p
0 0 00 10 0
0 1
0 1
0 1
G Gt t
( ) ( ) ( ) ( )
=
é
ë
ê
ê
ù
û
ú
ú
=
= = =
å å å
p pt p pt p pt pp p
k
k
n
k
k
n
n k
k
n
n0 0
0
1 0
0
0
0
01
, ,..., ,,..., . (2.161)
Ïåðåõîäÿ ê ïðåäåëàì â ðàâåíñòâå (2.156), ó÷èòûâàÿ ðàâåíñòâî (2.161),
ìîæíî çàïèñàòü

56
(p
0
,p
1
,...,p
n
) = (p
0
,p
1
,...,p
n
)×G(t). (2.162)
Ðàâåíñòâî (2.162) ìîæíî çàïèñàòü â âèäå ñèñòåìû óðàâíåíèé
p pp pp pp
p pp pp pp
p pp pp pp
nn
nn
n n n nnn
0 000 110 0
1 001 111 1
00 11
= + + +
= + + +
= + + +
ì
í
ï
î
ï
... ,
... ,
...........................
... .
(2.163)
Ñèñòåìà óðàâíåíèé (2.163) ëèíåéíî çàâèñèìà, îäíàêî åñëè îäíî ëþáîå
èç åå óðàâíåíèé çàìåíèòü íà î÷åâèäíîå ðàâåíñòâî (íîðìèðóþùåå óñëîâèå)
p
k
k
n
=
å
=
0
1, (2.164)
òî ïîëó÷åííàÿ ñèñòåìà n+1 óðàâíåíèé ñ íåèçâåñòíûìè p
0
, p
1
, ..., p
n
ìîæåò
áûòü èñïîëüçîâàíà äëÿ ïîëó÷åíèÿ ïðåäåëüíûõ âåðîÿòíîñòåé ñîñòîÿíèé.
Ôîðìóëû, ïîëó÷åííûå äëÿ ïðîñòûõ öåïåé Ìàðêîâà, â òåîðèè ñëó÷àé-
íûõ ôóíêöèé îáîáùàþòñÿ è íà äðóãèå ðàçíîâèäíîñòè ìàðêîâñêèõ ñëó÷àé-
íûõ ôóíêöèé, â òîì ÷èñëå ñ íåïðåðûâíûì âðåìåíåì è íåïðåðûâíûì èçìå-
íåíèåì çíà÷åíèé ñëó÷àéíîé ôóíêöèè.
2.3.3. Случайные потоки [3]
Ïîòîêîì îäíîðîäíûõ ñîáûòèé íàçûâàåòñÿ ñëó÷àéíûé ïðîöåññ, îáðà-
çîâàííûé ñîâîêóïíîñòüþ ñëó÷àéíûõ ìîìåíòîâ ïîÿâëåíèÿ ýòèõ ñîáûòèé
t
1
,t
2
,...,t
k
,t
k+1
,..., ãäå t
i
³ t
i–1
.  òåîðèè íàäåæíîñòè èññëåäóþòñÿ ñëó÷àéíûå
ïîòîêè äâóõ âèäîâ: ïîòîê ìîìåíòîâ îòêàçîâ è ïîòîê ìîìåíòîâ îêîí÷àíèÿ
âîññòàíîâëåíèé (ðåìîíòîâ).
 îáùåì ñëó÷àå äëÿ îïðåäåëåíèÿ ïîòîêà íåîáõîäèìî çàäàòü äëÿ êàæäî-
ãî n ³ 1 ðàñïðåäåëåíèå ñëó÷àéíîãî âåêòîðà (t
1
,t
2
,...,t
n
), ãäå t
k
=t
k
-t
k
-
1
, k ³
1, t
0
=0. Åñëè ñëó÷àéíûå âåëè÷èíû t
1
,t
2
,...,t
n
íåçàâèñèìû, òî òàêîé ïîòîê
íàçûâàåòñÿ ïîòîêîì ñ îãðàíè÷åííûì ïîñëåäåéñòâèåì è äëÿ åãî îïðåäå-
ëåíèÿ äîñòàòî÷íî çàäàòü íàáîð ôóíêöèé ðàñïðåäåëåíèÿ F
k
= p{t
k
£ t}, k ³ 1.
Ïîòîê ñ îãðàíè÷åííûì ïîñëåäåéñòâèåì, äëÿ êîòîðîãî
F
2
(t)=F
3
(t)=...=F
n
(t)=F(t), íàçûâàåòñÿ ðåêóððåíòíûì ïîòîêîì ñ çàïàç-
äûâàíèåì è îïðåäåëÿåòñÿ ôóíêöèÿìè ðàñïðåäåëåíèÿ F
1
(t) è F(t). Åñëè ê
òîìó æå è F
1
(t)=F(t), òî ïîòîê íàçûâàåòñÿ ïðîñòî ðåêóððåíòíûì ïîòî-
êîì.  ýòîì ñëó÷àå F(t) - ôóíêöèÿ ðàñïðåäåëåíèÿ äëèíû ïðîìåæóòêà ìåæ-
äó ëþáûìè äâóìÿ ïîñëåäîâàòåëüíûìè ñîáûòèÿìè.
Ðåêóððåíòíûé ïîòîê, ôóíêöèÿ ðàñïðåäåëåíèÿ êîòîðîãî ïîä÷èíÿåòñÿ
ýêñïîíåíöèàëüíîìó çàêîíó
F(t) = 1 - exp(–lt), l > 0, (2.165)
íàçûâàåòñÿ ïîòîêîì Ïóàññîíà (ïóàññîíîâñêèì ïîòîêîì), l (ñðåäíåå
÷èñëî ñîáûòèé â åäèíèöó âðåìåíè) íàçûâàåòñÿ èíòåíñèâíîñòüþ ïîòîêà.
Äëÿ ïóàññîíîâñêîãî ïîòîêà âåðîÿòíîñòü íàñòóïëåíèÿ ðîâíî k ñîáûòèé
â ïðîìåæóòêå âðåìåíè (t
0
, t)
( )
()
( )
( )
ptt pt
t
k
t k
k k
k
0
0, exp= = - ³
l
l
!
, (2.166)
57
íå çàâèñèò îò t
0
, ò.å. â ïóàññîíîâñêîì ïîòîêå âðåìÿ îæèäàíèÿ íîâîãî ñî-
áûòèÿ íå çàâèñèò îò âðåìåíè, ïðîøåäøåãî ïîñëå ïîñëåäíåãî ñîáûòèÿ (ïó-
àññîíîâñêèé ïðîöåññ îáëàäàåò ñâîéñòâîì îòñóòñòâèÿ ïîñëåäåéñòâèÿ).
Äëÿ ïóàññîíîâñêîãî ïîòîêà ìàòåìàòè÷åñêîå îæèäàíèå ñëó÷àéíîãî ÷èñ-
ëà m(t) ñîáûòèé çà âðåìÿ t
()
[ ]
()
Mmt kpt t
k
k
= =
=
¥
å
l
0
. (2.167)
Ïóàññîíîâñêèé ïîòîê ìîæíî îïðåäåëèòü òðåìÿ õàðàêòåðèñòè÷åñêèìè
ñâîéñòâàìè:
- ñâîéñòâî ñòàöèîíàðíîñòè: âåðîÿòíîñòíûå õàðàêòåðèñòèêè ïîòîêà
äëÿ ëþáîãî èíòåðâàëà âðåìåíè çàâèñÿò òîëüêî îò ïðîäîëæèòåëüíîñòè ýòî-
ãî èíòåðâàëà è íå çàâèñÿò îò ìîìåíòà åãî íà÷àëà;
- ñâîéñòâî îðäèíàðíîñòè: â áåñêîíå÷íî ìàëîì èíòåðâàëå âðåìåíè âå-
ðîÿòíîñòü ïîÿâëåíèÿ äâóõ è áîëåå ñîáûòèé - âåëè÷èíà áîëüøåãî ïîðÿäêà
ìàëîñòè, ÷åì âåðîÿòíîñòü ïîÿâëåíèÿ ðîâíî îäíîãî ñîáûòèÿ;
- ñâîéñòâî îòñóòñòâèÿ ïîñëåäåéñòâèÿ: íà÷èíàÿ ñ íåêîòîðîãî ìîìåí-
òà âðåìåíè âåðîÿòíîñòü ïîÿâëåíèÿ ñîáûòèÿ íå çàâèñèò îò ïðåäøåñòâóþ-
ùåé ðåàëèçàöèè ïîòîêà.
Åñëè ñîáûòèÿ ïîðîæäàþòñÿ íåñêîëüêèìè íåçàâèñèìûìè èñòî÷íèêàìè,
òî ñóììàðíûé ïîòîê, îáðàçîâàííûé ñóïåðïîçèöèåé (íàëîæåíèåì) èñõîä-
íûõ ïóàññîíîâñêèõ ïîòîêîâ, ÿâëÿåòñÿ òàêæå ïóàññîíîâñêèì ñ èíòåíñèâíî-
ñòüþ, ðàâíîé ñóììå èíòåíñèâíîñòåé ñëàãàåìûõ ïîòîêîâ, ò.å.
L
S
= =
=
å
l l
i
i
n
1
, (2.168)
ãäå l
i
- èíòåíñèâíîñòü i-ãî èñõîäíîãî ïîòîêà, n - ÷èñëî ïîòîêîâ.
 òåîðèè ìàññîâîãî îáñëóæèâàíèÿ äîêàçûâàåòñÿ, ÷òî ñóïåðïîçèöèÿ
ïðîèçâîëüíûõ íåçàâèñèìûõ ìåæäó ñîáîé ïîòîêîâ (íå îáÿçàòåëüíî ïóàññî-
íîâñêèõ) àñèìïòîòè÷åñêè ñõîäèòñÿ òàêæå ê ïóàññîíîâñêîìó ïîòîêó, åñëè
âëèÿíèå êàæäîãî èç íèõ ðàâíîìåðíî ìàëîå (òåîðåìà Ãðèãåëèîíèñà). Íà
ïðàêòèêå îáû÷íî ñóïåðïîçèöèÿ óæå 4 - 5 ïðàêòè÷åñêè ëþáûõ ïî âèäó ïî-
òîêîâ, îòâå÷àþùèõ óêàçàííûì óñëîâèÿì, ñîîòâåòñòâóåò õàðàêòåðèñòèêàì
ïóàññîíîâñêîãî ïîòîêà. Ïðè ýòîì èíòåíñèâíîñòü ñóììàðíîãî ïîòîêà
l
S
=
å
=
1
1
t
i
i
n
, (2.169)
ãäå t
i
- ñðåäíåå âðåìÿ ìåæäó äâóìÿ ñîñåäíèìè ñîáûòèÿìè â i-ì ïîòîêå.
2.3.4. Элементы теории массового обслуживания [3,12]
Îäíîé èç âîçìîæíîñòåé ïðàêòè÷åñêîãî ïðèìåíåíèÿ òåîðèè ñëó÷àéíûõ
ôóíêöèé ÿâëÿåòñÿ ðåøåíèå âåðîÿòíîñòíûõ çàäà÷, ñâÿçàííûõ ñ ðàáîòîé òàê
íàçûâàåìûõ ñèñòåì ìàññîâîãî îáñëóæèâàíèÿ (íàïðèìåð, òåëåôîííûõ ñòàí-
öèé, ðåìîíòíûõ ñëóæá, òîðãîâûõ îðãàíèçàöèé, áèëåòíûõ êàññ è ò.ä.). Ðà-
áîòà ñèñòåìû ìàññîâîãî îáñëóæèâàíèÿ ñîñòîèò â îáñëóæèâàíèè ïîñòó-
ïàþùåãî â íåå ñëó÷àéíîãî ïîòîêà òðåáîâàíèé.
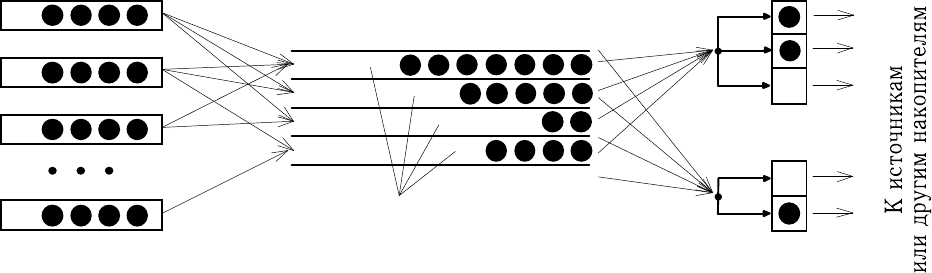
Äëÿ ñèñòåìû ìàññîâîãî îáñëóæèâàíèÿ äîëæíû áûòü çàäàíû (ðèñ.2.9):
58
1. Âõîäÿùèé ïîòîê òðåáîâàíèé - ìîìåíòû ïîñòóïëåíèÿ òðåáîâàíèé â
ñèñòåìó èç èñòî÷íèêà.
2. Ñèñòåìà îáñëóæèâàíèÿ, ñîñòîÿùàÿ èç óçëà îáñëóæèâàíèÿ, â êîòî-
ðîì ìîæåò áûòü îäèí èëè íåñêîëüêî îáñëóæèâàþùèõ óñòðîéñòâ (ïðèáî-
ðîâ), è íàêîïèòåëÿ, â êîòîðîì òðåáîâàíèÿ ìîãóò îæèäàòü îñâîáîæäåíèÿ
îáñëóæèâàþùèõ óñòðîéñòâ â îäíîé èëè íåñêîëüêèõ î÷åðåäÿõ.
3. Âðåìÿ îáñëóæèâàíèÿ òðåáîâàíèÿ êàæäûì óñòðîéñòâîì.
4. Äèñöèïëèíà îæèäàíèÿ, ðåãëàìåíòèðóþùàÿ êîëè÷åñòâî òðåáîâàíèé,
îäíîâðåìåííî íàõîäÿùèõñÿ â ñèñòåìå.
5. Äèñöèïëèíà î÷åðåäè, ðåãëàìåíòèðóþùàÿ ôîðìèðîâàíèå î÷åðåäåé.
6. Äèñöèïëèíà îáñëóæèâàíèÿ, ðåãëàìåíòèðóþùàÿ ïîñòóïëåíèå òðåáî-
âàíèé íà ñâîáîäíûå îáñëóæèâàþùèå óñòðîéñòâà.
Îáû÷íî ìîìåíòû ïîñòóïëåíèÿ òðåáîâàíèé â ñèñòåìó îáðàçóþò ñëó÷àé-
íûé ïîòîê, êîòîðûé ñ÷èòàåòñÿ ïóàññîíîâñêèì. Ýòî äîïóùåíèå òåì áîëåå
îïðàâäàíî äëÿ íåñêîëüêèõ èñòî÷íèêîâ, ñóïåðïîçèöèÿ ïîòîêîâ êîòîðûõ ïî
òåîðåìå Ãðèãåëèîíèñà àñèìïòîòè÷åñêè ñõîäèòñÿ ê ïóàññîíîâñêîìó è ìàëî
çàâèñèò îò òèïà èñõîäíûõ ïîòîêîâ. Äëÿ õàðàêòåðèñòèêè ïîòîêà äîñòàòî÷íî
çàäàòü çíà÷åíèå ìàòåìàòè÷åñêîãî îæèäàíèÿ ÷èñëà òðåáîâàíèé, ïîñòóïèâ-
øèõ çà åäèíèöó âðåìåíè l, ò.å. èíòåíñèâíîñòü ïîòîêà.  íåêîòîðûõ ñëó÷à-
ÿõ çàäàþòñÿ èíòåíñèâíîñòè ïîòîêîâ îò ðàçíûõ èñòî÷íèêîâ (l
1
, l
2
è ò.ä.).
Äëèòåëüíîñòü îáñëóæèâàíèÿ òðåáîâàíèé â óçëå îáñëóæèâàíèÿ òàêæå
îáðàçóåò ñëó÷àéíûé ïîòîê, êîòîðûé ìîæåò áûòü îïèñàí ìàòåìàòè÷åñêèì
îæèäàíèåì ÷èñëà òðåáîâàíèé, îáñëóæåííûõ âñåìè óñòðîéñòâàìè m (åñëè
âñå îíè çàíÿòû íåïðåðûâíî) èëè îòäåëüíî êàæäûì èç íèõ (m
1
, m
2
è ò.ä.).
Îòíîøåíèå j = l/m íàçûâàåòñÿ êîýôôèöèåíòîì çàãðóçêè ñèñòåìû.
Î÷åâèäíî ñòàáèëüíî ìîæåò ðàáîòàòü òîëüêî ñèñòåìà, â êîòîðîé j < 1.
Ñèñòåìû ìàññîâîãî îáñëóæèâàíèÿ îòëè÷àþòñÿ äðóã îò äðóãà äèñöèïëè-
íîé îæèäàíèÿ (â ñèñòåìàõ áåç îæèäàíèÿ åñëè âñå îáñëóæèâàþùèå óñò-
ðîéñòâà çàíÿòû, òî òðåáîâàíèå ïîëó÷àåò îòêàç, â ÷èñòûõ ñèñòåìàõ ñ
îæèäàíèåì - ñòàâèòñÿ â î÷åðåäü, â ñìåøàííûõ - ñòàâèòñÿ â î÷åðåäü, åñëè
÷èñëî òðåáîâàíèé â ñèñòåìå èëè íàêîïèòåëå è â óçëå îáñëóæèâàíèÿ íå
ïðåâûøàåò çàäàííîãî), äèñöèïëèíîé î÷åðåäè (â óïîðÿäî÷åííîé î÷åðåäè
ïîñòóïèâøåå òðåáîâàíèå ðàñïîëàãàåòñÿ ïîñëåäíèì, â äðóãèõ - ïåðâûì) è
äðóãèìè ïðèçíàêàìè.
Источники Накопитель Узел обслуживания
Обслуживающие
устройства
Очереди на обслуживание
Ðèñ.2.9. Ïðèìåð ñõåìû ñèñòåìû ìàññîâîãî îáñëóæèâàíèÿ

59
 êàæäûé ìîìåíò âðåìåíè ñèñòåìà ìîæåò õàðàêòåðèçîâàòüñÿ ÷èñëîì
òðåáîâàíèé â ñèñòåìå â öåëîì k, â íàêîïèòåëå m, â óçëå îáñëóæèâàíèÿ s,
÷èñëîì íåçàíÿòûõ îáñëóæèâàþùèõ óñòðîéñòâ l (èç îáùåãî ÷èñëà r) è äðó-
ãèìè ïàðàìåòðàìè. Î÷åâèäíî k = m+s è r = s+l. Ñèñòåìà, ïðîðàáîòàâøàÿ
äîñòàòî÷íî äëèòåëüíîå âðåìÿ, ìîæåò õàðàêòåðèçîâàòüñÿ âåðîÿòíîñòíûìè
ïàðàìåòðàìè: âåðîÿòíîñòüþ íàõîæäåíèÿ â ñèñòåìå k òðåáîâàíèé p
k
, ìàòå-
ìàòè÷åñêèìè îæèäàíèÿìè ÷èñëà òðåáîâàíèé â ñèñòåìå M(k), â íàêîïèòåëå
M(m), â óçëå îáñëóæèâàíèÿ M(s), ÷èñëà ñâîáîäíûõ óñòðîéñòâ M(l), âðåìå-
íè ïðåáûâàíèÿ â ñèñòåìå M(t) è â íàêîïèòåëå M(t
îæ
), äðóãèìè ïàðàìåòðà-
ìè. Î÷åâèäíî
() ( ) ( ) ()
Mk kp Mm krp Ms kp rp
k
k
n
k
kr
n
k
k
r
k
kr
n
= = - = +
= = = =+
å å å å
0 0 1
, , , (2.170)
() ( ) () ()
( )
( )
Ml r kp Mt Mk Mt Mm
k
k
r
= - = =
=
å
0
1 1
, ,
îæ
l l
, (2.171)
M(k) = M(m) + M(s), M(s) + M(l) = r. (2.172)
Ðàñ÷åò ñèñòåì ìàññîâîãî îáñëóæèâàíèÿ ÷àñòî âêëþ÷àåò â ñåáÿ ýêîíî-
ìè÷åñêèå àñïåêòû äëÿ îïòèìèçàöèè çàòðàò, íàïðèìåð, ïîëíîé ñòîèìîñòè
åäèíèöû âðåìåíè îæèäàíèÿ â íàêîïèòåëå è ïðîñòîÿ óçëà îáñëóæèâàíèÿ
( ) () ( ) ( )
C cMm cMl c k rp c r kp
k
k
r
n
k
k
r
= + = - + -
=
=
å å
1 2 1 2
0
, (2.173)
ãäå c
1
- ñòîèìîñòü åäèíèöû âðåìåíè îæèäàíèÿ îäíîãî òðåáîâàíèÿ, c
2
- ñòîèìîñòü åäèíè-
öû âðåìåíè ïðîñòîÿ îäíîãî îáñëóæèâàþùåãî óñòðîéñòâà.
Ìåòîäû ðàñ÷åòà ñèñòåì ìàññîâîãî îáñëóæèâàíèÿ ðàçíîîáðàçíû è ñïåöèôè÷íû, ìíî-
ãèå èç íèõ ïðèìåíèìû ëèøü ê ÷àñòíûì çàäà÷àì. Àíàëèòè÷åñêèå ìåòîäû ðàñ÷åòà ïðèìå-
íèìû ëèøü ê íåêîòîðûì ïðîñòåéøèì ñëó÷àÿì.
Ðàññìîòðèì â êà÷åñòâå ïðèìåðà ñìåøàííóþ ñèñòåìó ìàññîâîãî îáñëóæèâàíèÿ ñ
îäíèì îáñëóæèâàþùèì óñòðîéñòâîì, ñîñòîÿùóþ èç îäíîãî ðåìîíòíîãî óñòðîéñòâà è
îäíîé óïîðÿäî÷åííîé î÷åðåäè, ïðè÷åì â ñèñòåìå îäíîâðåìåííî ìîæåò íàõîäèòüñÿ íå
áîëåå n òðåáîâàíèé. Î÷åâèäíî, ìàðêîâñêàÿ ñëó÷àéíàÿ ôóíêöèÿ X(t) (÷èñëî òðåáîâàíèé
â ñèñòåìå) ìîæåò ïðèíèìàòü n+1 çíà÷åíèå: x
0
- â ñèñòåìå íåò òðåáîâàíèé, x
1
- îäíî
òðåáîâàíèå è ò.ä. äî x
n
(n òðåáîâàíèé).
Ïðè óñëîâèè îðäèíàðíîñòè âõîäÿùåãî ïîòîêà è ýêñïîíåíöèàëüíîãî çàêîíà ðàñïðå-
äåëåíèÿ âðåìåíè îáñëóæèâàíèÿ çà ìàëûé èíòåðâàë âðåìåíè Dt â ñèñòåìå ìîæåò ïðî-
èçîéòè íå áîëåå îäíîãî ñîáûòèÿ êàæäîãî âèäà (ïîñòóïëåíèÿ íîâîãî òðåáîâàíèÿ èëè
îêîí÷àíèÿ îáñëóæèâàíèÿ). Âåðîÿòíîñòè òîãî, ÷òî çà âðåìÿ Dt â ñèñòåìó íå ïîñòóïèò íè
îäíîãî òðåáîâàíèÿ è íè îäíî òðåáîâàíèå íå áóäåò îáñëóæåíî ïî ôîðìóëå (2.166):
()
( )
( )
( ) ( )
p t
t
t t t
0
0
0
1
l
lD
lD lD lDD = - = - » -
!
exp exp
, (2.174)
()
( )
( )
( ) ( )
p t
t
t t t
0
0
0
1
m
mD
mD mD mDD = - = - » -
!
exp exp
(2.175)
(çäåñü è äàëåå ïðè îïðåäåëåíèè âåðîÿòíîñòåé ñîáûòèé è ïåðåõîäîâ âåëè÷èíû âòîðîé è
âûøå ïîðÿäêîâ ìàëîñòè îòáðàñûâàþòñÿ).
Âåðîÿòíîñòè ïîñòóïëåíèÿ è îêîí÷àíèÿ îáñëóæèâàíèÿ îäíîãî òðåáîâàíèÿ:
()
( )
( )
( ) ( ) ( )
p t
t
t t t t t t
1
1
1
1
l
lD
lD lD lD lD lD lDD = - = × - » × - »
!
exp exp
, (2.176)
()
( )
( )
( ) ( ) ( )
p t
t
t t t t t t
1
1
1
1
m
mD
mD mD mD mD mD mDD = - = × - » × - »
!
exp exp
. (2.177)
60
 èíòåðâàëå âðåìåíè (t,t+Dt) â ñèñòåìå ìîãóò ñîñòîÿòüñÿ ñëåäóþùèå ïåðåõîäû:
1) êîëè÷åñòâî òðåáîâàíèé íå èçìåíèëîñü (ïåðåõîäû x
0
®x
0
, x
1
®x
1
, ..., x
n
®x
n
), ÷òî
ìîæåò ïðîèçîéòè â ÷åòûðåõ ñëó÷àÿõ:
- òðåáîâàíèé â ñèñòåìå íå áûëî (k=0) è çà âðåìÿ Dt íè îäíîãî òðåáîâàíèÿ íå ïî-
ñòóïèëî (ïåðåõîä x
0
®x
0
), âåðîÿòíîñòü ýòîãî ïî ôîðìóëå (2.174):
p
00
(t,t+Dt) =p
0
(
l
)
(Dt) » 1 – lDt; (2.178)
- òðåáîâàíèé áûëî k (0<k<n), çà âðåìÿ Dt íè îäíîãî íîâîãî òðåáîâàíèÿ íå ïîñòó-
ïèëî è íè îäíî íå îáñëóæåíî (ïåðåõîäû x
k
®x
k
), ïî ôîðìóëàì (2.174) è (2.175):
p¢
kk
(t,t+Dt) =p
0
(
l
)
(Dt)×p
0
(
m
)
(Dt) » (1 – lDt)(1 – mDt); (2.179)
- òðåáîâàíèé áûëî k (0<k<n), çà âðåìÿ Dt ïîñòóïèëî îäíî òðåáîâàíèå è îáñëóæè-
âàíèå îäíîãî áûëî çàêîí÷åíî (ïåðåõîäû x
k
®x
k
), ïî ôîðìóëàì (2.176) è (2.177):
p¢¢
kk
(t,t+Dt) =p
1
(
l
)
(Dt)×p
1
(
m
)
(Dt) » (lDt)(mDt); (2.180)
- òðåáîâàíèé áûëî n (k=n), çà âðåìÿ Dt íè îäíî òðåáîâàíèå íå îáñëóæåíî (ïåðåõîä
x
n
®x
n
), ïî ôîðìóëå (2.175):
p
nn
(t,t+Dt) =p
0
(
m
)
(Dt) » 1 - mDt; (2.181)
2) êîëè÷åñòâî òðåáîâàíèé â ñèñòåìå óâåëè÷èëîñü íà îäíî, ò.å. çà âðåìÿ Dt â ñèñòå-
ìó ïîñòóïèëî îäíî òðåáîâàíèå è íè îäíî òðåáîâàíèå íå áûëî îáñëóæåíî (ïåðåõîäû
x
k
®x
k+1
, 0<k<n–1), ïî ôîðìóëàì (2.176) è (2.177):
p
k(k+1)
(t,t+Dt) =p
1
(
l
)
(Dt)×p
0
(
m
)
(Dt) » lDt(1 - mDt) » lDt; (2.182)
3) êîëè÷åñòâî òðåáîâàíèé óìåíüøèëîñü íà îäíî, ò.å. çà âðåìÿ Dt â ñèñòåìó íå ïî-
ñòóïèëî íè îäíîãî òðåáîâàíèÿ è áûëî îáñëóæåíî îäíî òðåáîâàíèå (ïåðåõîäû x
k
®x
k–1
,
1<k<n), ïî ôîðìóëàì (2.174) è (2.177):
p
k(k
-
1)
(t,t+Dt) =p
0
(
l
)
(Dt)×p
1
(
m
)
(Dt) » (1 - lDt)mDt) » mDt. (2.183)
Î÷åâèäíî âåðîÿòíîñòü ïåðåõîäîâ x
k
®x
k
ïðè 0<k<n â öåëîì ñêëàäûâàåòñÿ èç âåðî-
ÿòíîñòåé äâóõ íåñîâìåñòíûõ ñîáûòèé (2.179) è (2.180):
p
kk
(t,t+Dt) =p
¢
kk
(t,t+Dt) + p
¢¢
kk
(t,t+Dt) » (1 - lDt)(1 - mDt) + lDt×mDt =
= 1 - lDt - mDt + 2lm(Dt)
2
» 1 - lDt - mDt = 1 - (l + m)Dt. (2.184)
Ìàòðèöà ïåðåõîäîâ G(Dt) áóäåò èìåòü ñëåäóþùèé âèä:
( )
( ) ( )
( ) ( )
( ) ( )
( ) ( ) ( ) ( ) ( )( ) ( )( ) ( )
( ) ( )
GDt
p p p p p p p
p p p p p p p
p p p p p p p
p p p p p p p
p p p p p p p
n n
n
n n
n
n n
n
n n n n n n n n n n
n n n n
nn nn
nn
= =
- -
- -
- -
- - - - - - - - -
- -
00 01 02 03
0 2 0 1
0
10 11 12 13
1 2 1 1
1
20 21 22 23
2 2 2 1
2
10 11 12 13 1 2 1 1 1
0 1 2 3
2 1
...
...
...
... ... ... ... ...... ... ...
...
...
( )
( )
( )
=
-
- +
- +
- +
-
1 0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 0 0 1
0 0 0 0 0 1
lD lD
mD l m lD
mD l m lD
mD l m lD
mD mD
t t
t t t
t t t
t t t
t t
...
...
...
... ... ... ......... ... ...
...
...
D
D
D
. (2.185)
Òîãäà â ñîîòâåòñòâèè ñ óðàâíåíèåì (2.56)
p(t+Dt) = p(t)×Ã(Dt), (2.186)
÷òî ðàâíîñèëüíî ñèñòåìå èç n+1 óðàâíåíèé (0<k<n):
(
)
(
)
(
)
(
)
( ) () () ( )
[ ]
()
( ) () ()( )
pt tpt tpt t
pt tp t tpt tp t t
pt t p t tpt t
k k k k
n n n
0 0 1
1 1
1
1
1
1
+ = - +
+ = + - + +
+ = + -
ì
í
ï
ï
î
ï
ï
- +
-
D
D D
D
lD mD
lD lm mD
lD mD
,
...
,
...
(2.187)
èëè
(
)
(
)
() ()
( ) ()
() ( ) () ()
( ) ()
() ()
pt t pt
t
pt pt
pt t pt
t
p t pt p t
pt t pt
t
p t pt
k k
k k k
n n
n n
0 0
0 1
1 1
1
+ -
=- +
+ -
= - + +
+ -
= -
ì
í
ï
ï
ï
ï
î
ï
ï
ï
ï
- +
-
D
D
D
D
D
D
l m
l l m m
l m
,
...
,
...
.
(2.188)
