Назаров А.С. (ред.) Конструирование радиоэлектронных средств

Подождите немного. Документ загружается.

q = Q/(τS)=P/S,

где S — площадь изотермической поверхности.

В общем случае теплообмен осуществляется с помощью трех видов

передачи тепла: теплопроводностью, конвекцией и излучением.

5.1.2. Передача тепла теплопроводностью

Теплопроводностью (кондукцией) называют перенос тепловой

энергии при соприкосновении частиц вещества или отдельных тел,

имеющих разные температуры.

Процесс передачи тепловой энергии теплопроводностью обычно

связывают с твердыми телами, но при определенных условиях он на-

блюдается также в жидкостях и газах.

При математическом описании про-

цесса теплопередачи принято считать,

что теплообмен происходит между изо-

термическими поверхностями, причем

изотермическая поверхность с большей

температурой отдает тепло изотермиче-

ским поверхностям с меньшей темпера-

турой.

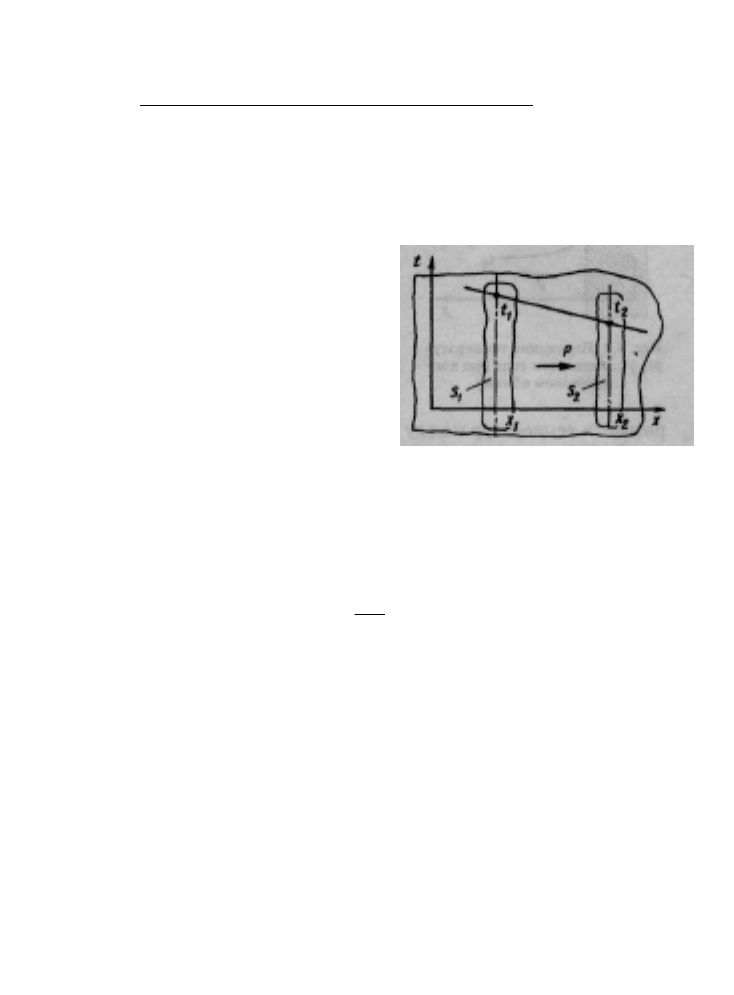
Если температурное поле изменяется

только в одном направлении (рис. 5.1),

то полный тепловой поток Р, передавае-

мый от изотермической поверхности 5 j

к изотермической поверхности S

, на основании закона Фурье может

быть записан в виде

)(

−=

(5.1)

где λ — коэффициент теплопроводности материала; S — площадь

средней изотермической поверхности : S = 0,5 (S

);t

, t

— температуры

изотермических поверхностей S

;l=x

—x

— расстояние между

изотермическими поверхностями.

Произведя замену λ /l = а

, из (5.1) получим:

= α

S(t

-t

), (5.2)

где а

— коэффициент теплопередачи кондукцией.

Значения коэффициентов теплопроводности наиболее распростра-

ненных конструкционных материалов приведены в табл. П.З приложе-

ния.

173

Рис. 5.1. Передача тепла

в изотропном твердом теле

5.1.3. Передача тепла конвекцией

Процесс теплообмена между поверхностью твердого тела с темпе-

ратурой t

и некоторой газообразной или жидкой средой с температурой

oбусловленный естественным или принудительным переме-

шиванием среды около поверхности, носит название конвективного

теплообмена.

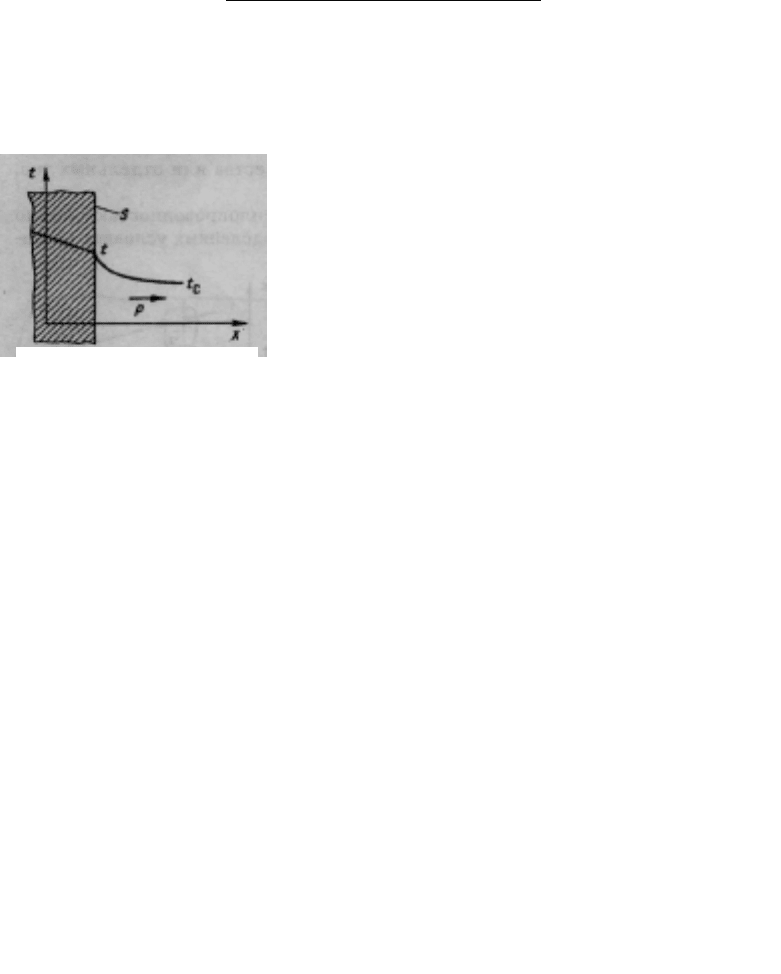
Полный тепловой поток, отдаваемый

изотермической поверхностью S среде за

счет конвекции (рис. 5.2), определяется в

соответствии с законом Ньютона следую-

щим образом:

= α

S(t

-t

), (5.3)

где α

— коэффициент конвективного теплообмена.

Коэффициент α

представляет собой тепловой

поток с единицы поверхности твердого тела в

окружающую среду при разности температур

между телом и средой в один градус.

В общем случае α

зависит от температур t

и t

и ряда физических

констант среды:

=f(t

. t

, β, λ., С

, v, a,g, Ф),

где β — коэффициент объемного расширения среды (жидкости или га-

за), К

-1

; λ. — коэффициент теплопроводности, или просто теплопро-

водность среды, Вт/(м • К); С

— удельная теплоемкость среды при оп-

ределенном давлении, Дж/(кг • К); v — коэффициент кинематической

вязкости среды, м

/с; g — ускорение силы тяжести, м/с

; а = λ./С

ρ —

температуропроводность среды, м

/с; р — плотность среды, кг/м

;

Ф — совокупность параметров, характеризующих форму и поверхность

тел.

Зависимость физических констант среды от температур t

.и t

бесконечное разнообразие форм поверхности нагретых тел исключают

возможность получения табличных значений конвективных коэффици-

ентов теплопередачи как теоретическими, так и экспериментальными

методами.

Поэтому для определения α

используются основные положения

теории подобия. Согласно этой теории сложные процессы характеризу-

174

Рис. 5.2. Изменение

температу-

ры у пов

ерхности тела при

кон

ются не отдельными частными параметрами, а обобщенными, представ-

ляющими собой безразмерные комплексы размерных физических вели-

чин. Если значения обобщенных параметров находятся в определенном

диапазоне величин, то процессы (явления) считаются подобными. В те-

ории теплообмена используются четыре обобщенных параметра (кри-

терия), каждый из которых выражается через определенное количество

физических параметров среды. Знание критериев позволяет без особых

затруднений найти α

Критерии подобия (критериальные уравнения). Для определения

конвективного коэффициента теплопередачи в условиях естественной

и принудительной (вынужденной) конвекции достаточно определить:

критерий Нуссельта

α L

(5.4)

где L — определяющий геометрический размер тела (внутренний диа-

метр трубы, высота цилиндра или вертикальной стенки, наименьшая

сторона горизонтально расположенной поверхности и т.п.);

критерий Грасгофа

)(

gGr −= β

(

критерий Прандтля

=Pr

(5.6)

критерий Рейнольдса

=Re

(5.7)

где v — скорость движения газа или жидкости при вынужденной кон-

векции.

Из (5.4) видно, что коэффициент α

выражается через критерий

Нуссельта. В зависимости от условий конвективного теплообмена α

определяется одним из рассматриваемых далее способов.

Определение α

при естественной конвекции в неограниченном

пространстве. Данный случай характерен для теплопередачи от корпу-

са блока или устройства в окружающую среду. Критерий Нуссельта вы-

числяется с помощью соотношения

175

Nu = C(GrPr)

, (5.8)

где С и п — показатели теплообмена, которые приведены в табл. 5.1.

Таблица 5.1

(GrPr)^ С л Режим движения газа (жидкости)

-3

0,5 0 Пленочный поток

-3

...5·10

1,18 1/8 Ламинарный

5·10

...2·10

0,54 1/4 Переходный

2·10

... 10

0,136 1/3 Вихревой (турбулентный)

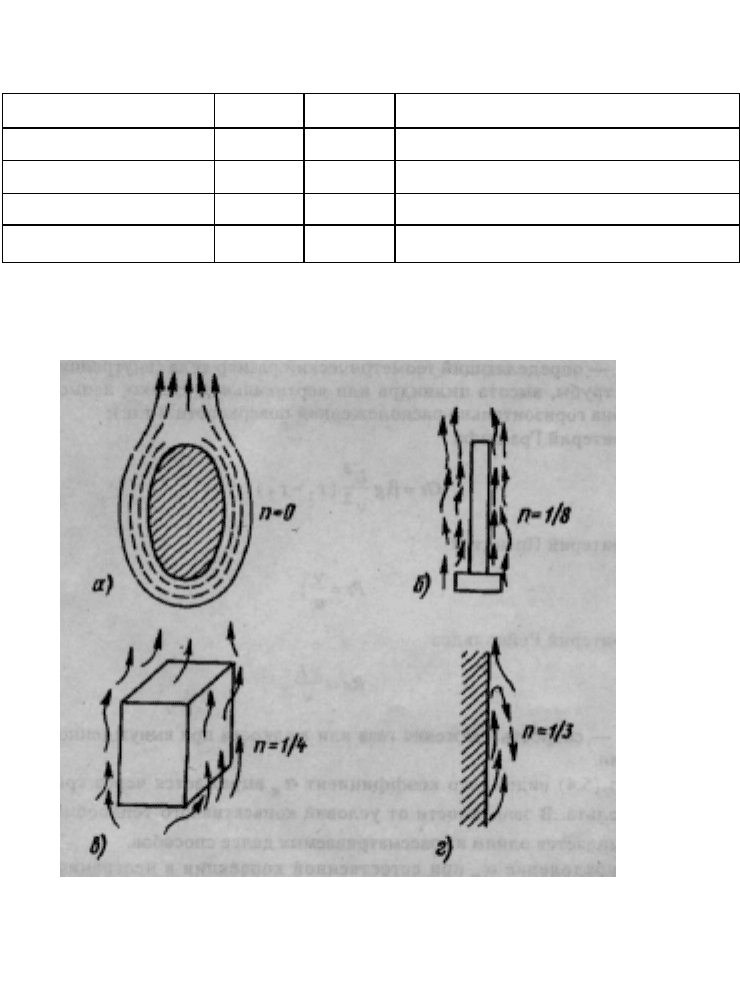
Показатель степени п характеризует режим движения газа (жидко-

сти). Виды потоков, соответствующих различным значениям, условно

показаны на рис. 5.3.

Рис. 5.3. Характер движения теплоносителя у поверхности нагретых тел:

а — пленочный поток; б — ламинарный поток; в — переходный режим;

г — вихревой режим

176

С увеличением п поток становится менее направленным и более

интенсивным и передача тепла увеличивается. Интенсивность теплопе-

редачи в значительной мере зависит от температуры поверхности тела,

физических свойств среды и в меньшей степени — от объема и формы

тела.

Таким образом, для определения α

при_естественной конвекции^

неограниченном пространстве необходимо:

в табл. П.5 приложения взять значения физических констант среды

для средней температуры

= 0,5(f

рассчитать критерий Gr и Рr и найти их произведение:

из табл. 5.1 определить показатели теплообмена, по формуле (5.8) —

критерий Nu и с помощью формулы (5.4) — коэффициент α

Применение критериальных уравнений при анализе теплообмена

тел в случае естественной конвекции в неограниченном пространстве

позволяет получить формулы для непосредственного определения

конвективного коэффициента теплопередачи в воздушной среде. Тела

ограничиваются плоскими, цилиндрическими и сферическими поверх-

ностями. Каждое тело характеризуется определяющим, размером L и

ориентацией поверхности в пространстве — коэффициентом N.

Если определяющий размер L и разность температур поверхности

теплообмена и окружающей среды t

-1

удовлетворяют неравенству

-t

)<[840/(L-10

-3

)]

(5.9)

то движение воздуха подчиняется закону степени 1/4 (переходный ре-

жим), в противном случае имеет место теплообмен по закону степени

1/3 (вихревой режим).

Расчет конвективного коэффициента теплопередачи для переход-

ного режима производят по формуле

= (1,42+1,4.10

-3

ср

)N[(t

-t

)/L,]

1/4

, (5.10)

для вихревого режима — по формуле

= (l,67+3,6.10

-3

)N(t

-t

)

1/3

, (5.11)

где t

ср

= 0,5 (t

) — средняя температура окружающей среды.

Значения коэффициента N приведены в табл. 5.2

177

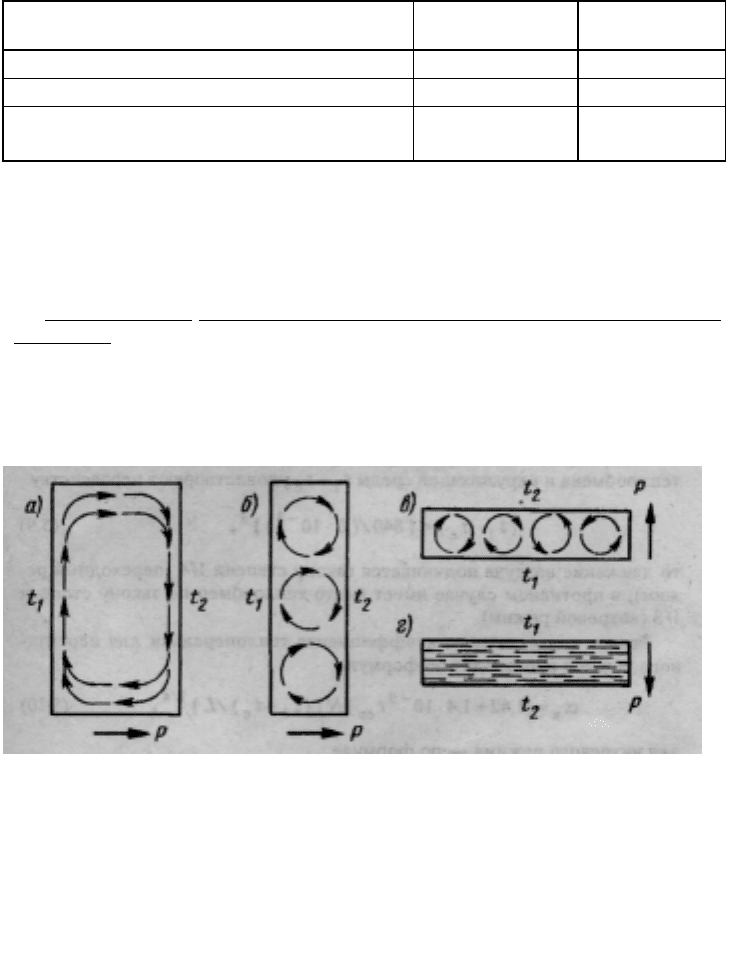
Таблица 5.2

Вид поверхности

Определяющий

размер

Значение

Сферическая, горизонтальные цилиндры

Диаметр 1,0

Вертикальные пластины и цилиндры Высота 1,0

Горизонтальные пластины,рассеивающие

потоки:вверх,вниз

Максимальный

размер

1,3

0,7

Формулы (5.9)—(5.11) позволяют при анализе теплового режима

конструкций РЭС в форме прямоугольного параллелепипеда предста-

вить кожух моделями горизонтальных и вертикальных пластин и рас-

считать конвективный коэффициент теплопередачи от каждой стенки

кожуха.

Определение α

при естественной конвекции в ограниченном про-

странстве. Данный случай отражает процесс теплообмена между внут-

ренними, размещенными в корпусе, элементами конструкции РЭС за

счет естественного движения газа (жидкости) в каналах теплообмена.

Такими каналами являются воздушные прослойки между кожухом и на-

гретой зоной, зазоры между функциональными ячейками и т.п. Харак-

тер движения газа (жидкости) в каналах показан на рис. 5.4.

Рис. 5.4. Характер движения теплоносителя в каналах теплообмена:

а — конвективный поток в широком канале;

б, в — локальные конвективные потоки в узких каналах;

г — отсутствие конвекции

Процесс конвективного теплообмена в ограниченном пространстве

более сложен, так как происходит одновременное нагревание газа

178

(жидкости), холодной стенки и охлаждение нагретой. При этом эф-

фективность конвекции зависит от разности температур нагретой и хо-

лодной стенок канала Δt и расстояния между стенками δ. Так, напри-

мер, в воздушных прослойках толщиной более 10 мм конвекция насту-

пает при перегреве Δt = 0,3°C. В прослойках до 10 мм конвективное

движение воздуха наблюдается, если Δt > 5° С . В прослойках с толщи-

ной менее 5 мм конвективный теплообмен возникает, если Δ t не ниже

100°С. Для упрощения расчетов конвективного коэффициента тепло-

передачи в ограниченном пространстве предполагается, что тепло от

нагретой стенки к холодной передается за счет теплопроводности среды,

находящейся между стенками. При этом теплофизические свойства

среды характеризуют эквивалентным коэффициентом теплопроводности

= к

λ, (5.12)

где k

=f(GrPr) — поправочный коэффициент на конвективный теп-

лообмен в прослойке (коэффициент конвекции); λ — коэффициент

теплопроводности среды при среднеарифметической температуре по-

верхностей t

= 0,5 (t

);t

— соответственно температуры нагретой и

холодной стенок.

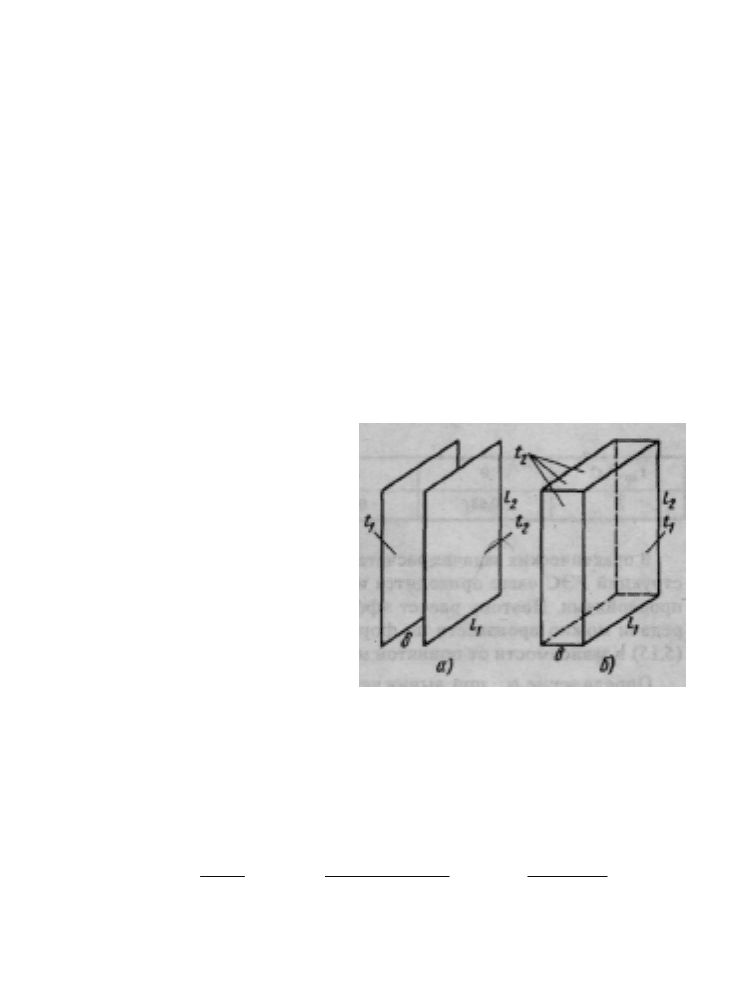
Соотношения для расчета ко-

эффициента теплообмена в огра-

ниченном пространстве получены

[19] в результате моделирования

теплопередачи между поверхно-

стями, разделенными газовой или

жидкостной прослойкой толщи-

ной δ, и в прямоугольном парал-

лелепипеде, одна грань которого

с размерами l

, l

имеет темпера-

туру t

, остальные — температуру

, причем t

> t

(рис. 5.5).

Эффективные коэффициенты

теплопередачи в плоской, цилин-

дрической и сферической про-

слойках находят согласно выра-

жениям:

КП

= ;

)/ln(

121

ddd

КЦ

α = ;

dк

КС

α =

где d

, d

— диаметры внутреннего и внешнего цилиндров (сфер).

179

Рис.

5.5. Моделирование ограниченного

пространства:

а —прослойка между плоскими стенка-

ми; б — прямоугольный параллелепипед

Для неограниченных плоских, цилиндрических и сферических про-

слоек коэффициент конвекции к

= 1 при условии GrPr≤ 10 . Если

произведение GrPr> 10

, то коэффициент конвекции приближенно

можно найти по формуле

= 0,18(GrPr)

(5.14)

где п = 0,25— показатель теплообмена.

Эффективный коэффициент теплопередачи через воздушную про-

слойку в прямоугольном параллелепипеде (см. рис. 5.5) определяется

из выражения

[

]

3/5

21..

/)/1(25.525.6 δδα tBllN

ПК

∆+−=

−

(5.15)

где δ— толщина прослойки; N = 1 и N = 1,3 — коэффициенты для

вертикальной и горизонтальной ориентации прослойки соответствен-

но, причем в случае горизонтальной ориентации нагретая грань парал-

лелепипеда находится внизу; В — коэффициент, зависящий от средней

температуры воздуха в прослойке t

СР

= 0,5 (t

Значения коэффициента В приведены в табл. 5.3

Таблица 5.3

tср. 'С 0 50 100 200

B 0,63 0,58 0,56 0,44

В практических задачах расчета показателей теплового режима кон-

струкций РЭС чаще приходится иметь дело с плоскими воздушными

прослойками. Поэтому расчет эффективного коэффициента теплопе-

редачи можно произвести по формулам (5.13) совместно с (5.14) или

(5.15) в зависимости от принятой модели.

Определение α

при вынужденной конвекции. Вынужденная кон-

векция обусловлена принудительным перемещением жидкости или га-

за относительно поверхности нагретого тела; появляется в результате

работы вентиляторов, воздуходувок, жидкостных насосов и т.п. Расчет

конвективного коэффициента теплопередачи сводится к определению

режима движения жидкости или газа и критерия Нуссельта.

Режим движения жидкости (газа) зависит от критерия Рейнольдса:

для ламинарного потока — Re < 2200, для переходного —2200 ≤Re ≤ 10

, для

вихревого — Re ≥ 10

. Ввиду того что переходный режим соответствует

относительно малой области значений числа Рей-

180

нольдса, расчеты теплообмена при вынужденной конвекции проводят

для двух режимов: ламинарного и вихревого. Переход от ламинарного

режима к вихревому определяют по значению критического числа

= 5·10

-5

Скорость принудительного движения жидкости (газа), от которой

зависит число Re, находят через объемный расход жидкости (газа) G

в системе охлаждения и площадь среднего сечения потока A

ср

V=G

. (5.16)

Для систем принудительного воздушного охлаждения в качестве

параметра A

ср

выступает средняя площадь сечения воздушного

канала,для жидкостного принудительного охлаждения — площадь сечения

трубы.

В схеме расчета α

при вынужденной конвекции критерий Nu вы-

числяется через критерий Re. Однако подход к определению критерия

Nu зависит как от режима движения жидкости (газа), так и от условий

взаимодействия потока и охлаждаемой поверхности. Поэтому выделя-

ют вынужденную конвекцию при внешнем обтекании тел и вынужден-

ную конвекцию в каналах и трубах. В свою очередь, при внешнем обте-

кании тел рассматривают случаи продольного и поперечного движений

потока жидкости или газа.

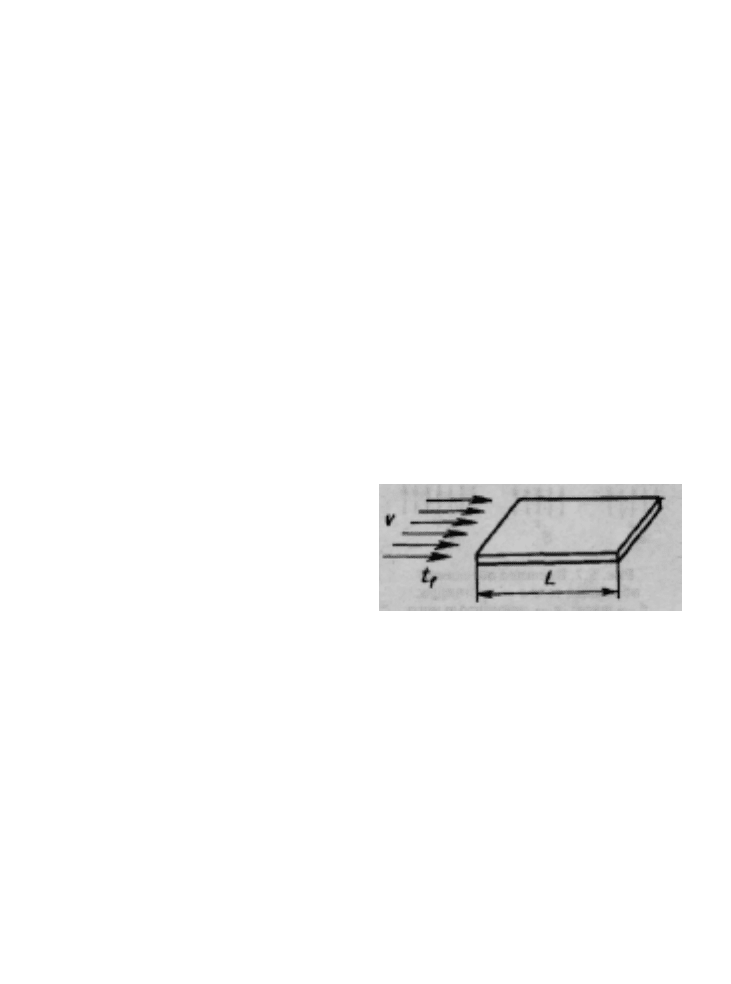
Анализ конвективной теплопере-

дачи при продольном внешнем

обтекании тел производится на

модели в виде теплоотдающей

стенки, ориентированной вдоль

потока, движущегося со скоростью v

при температуре t

(рис. 5.16).

Определяющим является размер стенки

вдоль потока L.

При ламинарном движении жидкости, когдаRе

<5·10

, выраже-

ние для расчета критерия Нуссельта имеет вид

=0,66Re

0.5

.0.43

(Pr

/Pr

)

0.25

, (5.17)

где индексы f и w означают, что соответствующие критерии опреде-

лены для температуры потока и температуры стенки. В выражении

(5.17) влияние физических свойств жидкости и их зависимость от тем-

пературы учитываются параметром Pr

.0.43

, а влияние направления

теплового потока и род жидкости — параметром (Pr

/Pr

)

0.25

181

Рис. 5.6.

Продольное

внешнее

обтекание тела

Для воздуха в широком диапазоне температур Pr

=Prw = 0,7, поэтому

формула (5.17) преобразуется к виду

Nu Re57.0= (5.18)

В случае вихревого движения жидкости (R

≥5·10

) расчет критерия

Нуссельта производится по формуле

= 0,031Re°'

Pr°'

(Pr

/Pr

)

0.25

. (5.19)

Преобразование (5.19) с учетом приведенного выше условия дает

формулу расчета критерия Нуссельта при вихревом движении воздуха:

=0,032Re

0.8

(5.20)

В приближенных расчетах формулы (5.17) и (5.19) можно использо-

вать для анализа теплообмена цилиндрических поверхностей, омывае-

мых продольным потоком жидкости [19].

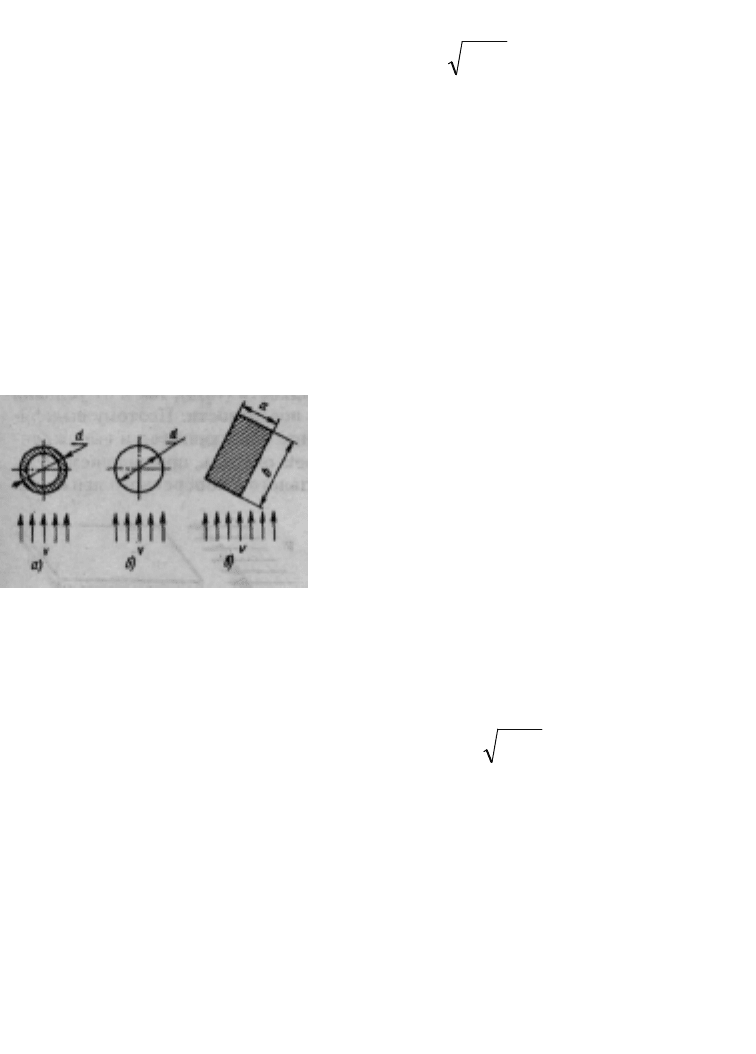
Поперечное движение потока ха-

рактерно для внешнего обтекания

объемных тел различных геометриче-

ских форм воздухом. В качестве опре-

деляющего размера тела принимается

длина обтекания L тела потоком

воздуха. Длина обтекания для цилиндра и

шара составляет L = 0,5πd, для

прямоугольного параллелепипеда —

L = a + b (рис. 5.7).

При значениях числа Рейнольдса

10 < Re < 10

приближенное выражение для

расчета критерия Нуссельта

может быть записано в виде

Nu Re8.0= (5.21)

Формула (5.21) применяется при расчете конвективного коэффици-

ента теплообмена тел, находящихся в замкнутом пространстве и омыва-

емых поперечным потоком воздуха. Определяющий размер в этом слу-

чае находят согласно рис. 5.7, а скорость движения воздуха относи-

тельно поверхности тела определяется по формуле (5.16).

Для конструкции РЭС с неупорядоченным расположением элемен-

тов площадь среднего сечения потока А

и определяющий размер

(длина обтекания) L могут быть оценены по формулам:

182

Рис.

5.7. Внешнее

обтекание

объемных тел: а —

цилиндра;

—

шара; в

—