Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

where is a path-ordering operator along γ(t).

The horizontal lift is expressed

as ˜γ(t) = σ

(γ (t))g

(γ (t)).

Corollary 10.1. Let ˜γ



be another horizontal lift of γ , such that ˜γ



(0) = γ(0)g.

Then ˜γ



(t) =˜γ(t)g for all t ∈[0, 1].

Proof. We ﬁrst note that the horizontal subspace is right invariant, R

g∗

P =

P.Let˜γ be a horizontal lift of γ .Then˜γ

: t →˜γ(t)g is also a horizontal

lift of γ(t) since its tangent vector belongs to H

˜γ g

P. From theorem 10.2 we ﬁnd

˜γ



is the unique horizontal lift which starts at ˜γ(0)g.

Example 10.2. Let us consider the bundle P(M, )

∼

M × where M =

−{0}.Letφ : ((x, y), f ) → u ∈ P be a local trivialization, where (x, y) are

the coordinates of M while f is that of the additive group

.Let

ω =

ydx − xdy

+ y

+ d f

be a connection one-form. It is easily veriﬁed that ω satisﬁes the axioms of

the connection one-form. In fact, for A

= A∂/∂f , A ∈ beinganelement

of the Lie algebra of additive group, we have ω(A

) = A.Furthermore,

g∗

ω = ω = g

−1

ωg,since is Abelian. Let γ :[0, 1]→M be a

curve t → (cos 2π t, sin 2πt). Let us work out a horizontal lift which starts at

((1, 0), 0).Let

X =

≡

∂

∂x

∂

∂y

d f

∂

∂ f

be tangent to ˜γ(t).ForX to be horizontal, it must satisfy

0 = ω(X ) =

−

d f

=−2π +

d f

The solution is easily found to be f = 2πt + constant. We ﬁnally ﬁnd the

horizontal lift ˜γ passing through ((1, 0), 0),

˜γ(t) = ((cos 2πt, sin 2πt), 2πt) (10.15)

which is a helix over the unit circle.

Under the group action (right or left does not matter), f translates to

f + g, g ∈

. The shifted horizontal lift is

˜γ

(t) = ((cos 2π t, sin 2πt), 2πt + g). (10.16)

iµ

(γ (t)) and

iν

(γ (s)) do not commute in general and the exponential in (10.14) is not well

deﬁned as it is. Let A(t) and B(t) be t-dependent matrices. Then the action of

[A(t)B(s)]=



A(t)B(s)(t > s)

B(s) A(t)(s > t).

Generalization to products of more matrices should be obvious.

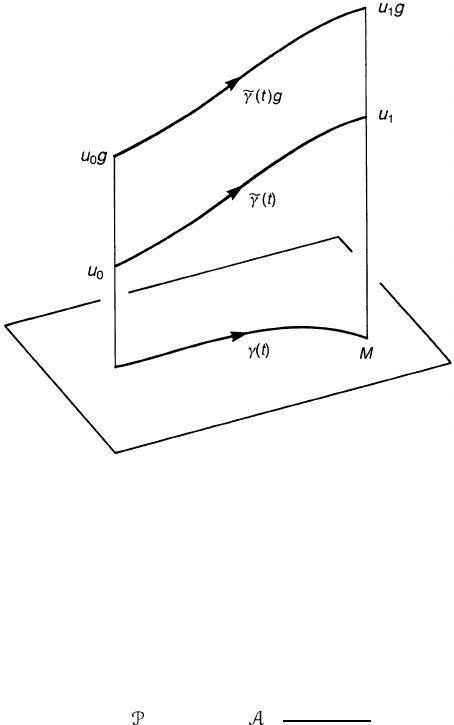
Figure 10.3. Acurveγ(t ) in M and its horizontal lifts ˜γ(t ) and ˜γ(t)g.

Let γ :[0, 1]→M be a curve. Take a point u

∈ π

−1

(γ (0)).Thereis

a unique horizontal lift ˜γ(t) of γ(t) through u

, and hence a unique point u

˜γ(1) ∈ π

−1

(γ (1)), see ﬁgure 10.3. The point u

is called the parallel transport

of u

along the curve γ . This deﬁnes a map ( ˜γ) : π

−1

(γ (0)) → π

−1

(γ (1))

such that u

→ u

. If the local form (10.14) is employed, we have

= σ

(1) exp



−



iµ

(γ (t))



. (10.17)

Corollary 10.1 ensures that ( ˜γ) commutes with the right action R

.First

note that R

( ˜γ)(u

) = u

g and ( ˜γ)R

) = ( ˜γ)(u

g). Observe that ˜γ(t)g

is a horizontal lift through u

g and u

g. From the uniqueness of the horizontal

lift through u

g,wehaveu

g = ( ˜γ)(u

g),thatisR

( ˜γ)(u

) = ( ˜γ)R

Since this is true for any u

∈ π

−1

(γ (0)),wehave

( ˜γ) = ( ˜γ)R

. (10.18)

Exercise 10.3. Let ˜γ be a horizontal lift of γ :[0, 1]→M. Consider a map

( ˜γ

−1

) : π

−1

(γ (1)) → π

−1

(γ (0)) where ˜γ

−1

(t) =˜γ(1 −t). Show that

( ˜γ

−1

) = ( ˜γ)

−1

. (10.19)

Consider two curves α :[0, 1]→M and β :[0, 1]→M such that

α(1) = β(0). Deﬁne the product α ∗ β by

α ∗ β =



α(2t) 0 ≤ t ≤

β(2t − 1)

≤ t ≤ 1.

Let ( ˜α) : π

−1

(α(0)) → π

−1

(α(1)) and (

β) : π

−1

(β(0)) → π

−1

(β(1)).

Show that

(

α ∗ β) = (

β) ◦ (˜α). (10.20)

Exercise 10.4. Let us write u ∼ v,ifu,v ∈ P are on the same horizontal lift.

Show that ∼ is an equivalence relation.

10.2 Holonomy

10.2.1 Deﬁnitions

Let P(M, G) be a principal bundle and let γ :[0, 1]→M be a curve whose

horizontal lift through u

∈ π

−1

(γ (0)) is ˜γ . In the last section, we deﬁned

amap( ˜γ) : π

−1

(γ (0)) → π

−1

(γ (1)) which maps a point u

=˜γ(0) to

=˜γ(1). Let us consider two curves α, β :[0, 1]→M with α(0) = β(0) = p

and α(1) = β(1) = p

. Take horizontal lifts ˜α and

β of α and β such that

˜α(0) =

β(0) = u

.Then˜α(1) is not necessarily equal to

β(1). This shows that if

we consider a loop γ :[0, 1]→M at p = γ(0) = γ(1),wehave ˜γ(0) =˜γ(1) in

general. A loop γ deﬁnes a transformation τ

: π

−1

( p) → π

−1

( p) on the ﬁbre.

This transformation is compatible with the right action of the group,

(ug) = τ

(u)g (10.21)

which follows immediately from (10.18). We note that τ

depends not only on

the loop γ but also on the connection.

Example 10.3. Consider an

-bundle over M =

−{0}. The connection

one-form ω and the loop γ in example 10.2 deﬁne a map τ

: π

−1

((1, 0)) →

−1

((1, 0)) given by g → g + 2π, g ∈ .

Take a point u ∈ P with π(u) = p and consider the set of loops C

(M) at

p; C

(M) ≡{γ :[0, 1]→M|γ(0) = γ(1) = p}. The set of elements



≡{g ∈ G|τ

(u) = ug,γ ∈ C

(M)} (10.22)

is a subgroup of the structure group G and is called the holonomy group at u.The

group property of 

is easily derived from exercise 10.3. If α, β and γ = α ∗ β

are loops at p,wehaveτ

= τ

◦ τ

, hence

(u) = τ

◦ τ

(u) = τ

(ug

) = τ

(u)g

= ug

where τ

(u) = ug

etc. This shows that

= g

. (10.23)

The constant loop c :[0, 1] → p deﬁnes the identity transformation

: u → u. The inverse loop γ

−1

of γ induces the inverse transformation

−1

= τ

−1

, hence g

−1

= g

−1

Exercise 10.5. (a) Let τ

(u) = ug

. Show that

(ug) = ug(ad

) = ug(g

−1

g). (10.24)

Verify that



∼

−1



a. (10.25)

(b) Let u, u



∈ P be points on the same horizontal lift ˜γ . Show that



∼





are isomorphic to each

other.

Exercise 10.6. Let

iµ

be a gauge potential over U

and γ a loop in

.Letτ

(u) = ug

, u ∈ P, g

∈ G. Use (10.14) to show that

= exp



−

iµ



. (10.26)

Let C

(M) denote the set of loops at p, which are homotopic to the constant

loop at p. The group



≡{g ∈ G|τ

(u) = ug,γ ∈ C

(M)} (10.27)

is called the restricted holonomy group.

10.3 Curvature

10.3.1 Covariant derivatives in principal bundles

We deﬁned the exterior derivative d : 

(M) → 

r+1

(M) in chapter 5. An

r-form η is a real-valued form acting on vectors,

η : TM∧ ...∧ TM →

We will generalize this operation so that we can differentiate a vector-valued r-

form φ ∈ 

(P) ⊗ V ,

φ : TP∧ ...∧ TP → V

where V is a vector space of dimension k. The most general form of φ is

φ =



α=1

⊗ e

, {e

} being a basis of V and φ

∈ 

(P).

A connection ω on a principal bundle P(M, G) separates T

P into H

P ⊕

P. Accordingly, a vector X ∈ T

P is decomposed as X = X

+ X

where

∈ H

P and X

∈ V

Deﬁnition 10.4. Let φ ∈ 

(P) ⊗ V and X

,...,X

r+1

∈ T

P.Thecovariant

derivative of φ is deﬁned by

Dφ(X

,...,X

r+1

) ≡ d

φ(X

,...,X

r+1

) (10.28)

where d

φ ≡ d

⊗ e

10.3.2 Curvature

Deﬁnition 10.5. The curvature two-form  is the covariant derivative of the

connection one-form ω,

 ≡ Dω ∈ 

(P) ⊗ . (10.29)

Proposition 10.2. The curvature two-form satisﬁes (cf (10.3b))

∗

 = a

−1

aa∈ G. (10.30)

Proof. We ﬁrst note that (R

a∗

= R

a∗

) (R

a∗

preserves the horizontal

subspaces) and d

∗

= R

∗

, see (5.75). By deﬁnition we ﬁnd

∗

(X, Y ) = (R

a∗

X, R

a∗

Y ) = d

ω((R

a∗

,(R

a∗

Y )

)

= d

ω(R

a∗

, R

a∗

) = R

∗

ω(X

, Y

)

= d

∗

ω(X

, Y

)

= d

−1

ωa)(X

, Y

) = a

−1

ω(X

, Y

= a

−1

(X, Y )a

where we noted that a is a constant element and hence d

a = 0.

Take a -valued p-form ζ = ζ

⊗ T

and a -valued q-form η = η

⊗ T

where ζ

∈ 

(P), η

∈ 

(P),and{T

} is a basis of . Deﬁne the commutator

of ζ and η by

[ζ,η]≡ζ ∧ η − (−1)

η ∧ ζ

= T

∧ η

− (−1)

∧ ζ

=[T

, T

]⊗ζ

∧ η

= f

αβ

⊗ ζ

∧ η

. (10.31)

If we put ζ = η in (10.31), when p and q are odd, we have

[ζ,ζ]=2ζ ∧ ζ = f

αβ

⊗ ζ

∧ ζ

Lemma 10.2. Let X ∈ H

P and Y ∈ V

P.Then[X, Y ]∈H

Proof.LetY be a vector ﬁeld generated by g(t),then

X =[Y, X]=lim

t→0

−1

g(t )∗

X − X ).

Since a connection satisﬁes R

g∗

P = H

P, the vector R

g(t )∗

X is horizontal

andsois[Y, X].

Theorem 10.3. Let X, Y ∈ T

P.Then and ω satisfy Cartan’s structure

equation

(X, Y ) =d

ω(X, Y ) +[ω(X ), ω(Y )] (10.32a)

which is also written as

 = d

ω + ω ∧ ω. (10.32b)

Proof. We consider the following three cases separately:

(i) Let X, Y ∈ H

P.Thenω(X) = ω(Y ) = 0 by deﬁnition. From deﬁnition

10.5, we have (X, Y ) = d

ω(X

, Y

) = d

ω(X, Y ),sinceX = X

and

= Y

(ii) Let X ∈ H

P and Y ∈ V

P.SinceY

= 0, we have (X, Y ) = 0. We

also have ω(X) = 0. Thus, we need to prove d

ω(X, Y ) = 0. From (5.70), we

obtain

ω(X, Y ) = X ω(Y ) − Y ω(X ) −ω([X, Y ]) = X ω(Y ) − ω([X, Y ]).

Since Y ∈ V

P, there is an element V ∈ such that Y = V

.Thenω(Y ) = V is

constant, hence X ω(Y ) = X · V = 0. From lemma 10.2, we have [X, Y ]∈H

so that ω([X, Y ]) = 0andweﬁndd

ω(X, Y ) = 0.

(iii) For X, Y ∈ V

P,wehave(X, Y ) = 0. We ﬁnd that, in this case,

ω(X, Y ) = X ω(Y ) − Y ω(X) − ω([X, Y ]) =−ω([X, Y ]).

We note that X and Y are closed under the Lie bracket, [X, Y ]∈V

P, see exercise

10.1(b). Then there exists A ∈

such that

ω([X, Y ]) = A

where A

=[X, Y ].LetB

= X and C

= Y .Then[ω(X), ω(Y )]=[B, C]=

A since [B, C]

=[B

, C

]. Thus, we have shown that

0 = d

ω(X, Y ) + ω([X, Y ]) = d

ω(X, Y ) +[ω(X), ω(Y )].

Since  is linear and skew symmetric, these three cases are sufﬁcient to show

that (10.32) is true for any vectors.

To derive (10.32b) from (10.32a), we note that

[ω, ω](X, Y ) =[T

, T

]ω

∧ ω

(X, Y )

=[T

, T

][ω

(X )ω

(Y ) − ω

(X )ω

(Y )]

=[ω(X), ω(Y )]−[ω(Y ), ω(X )]=2[ω(X), ω(Y )].

Hence, (X, Y ) = (d

ω +

[ω, ω])(X, Y ) = (d

ω + ω ∧ω)(X, Y ).

10.3.3 Geometrical meaning of the curvature and the Ambrose–Singer

theorem

We have shown in chapter 7 that the Riemann curvature tensor expresses the non-

commutativity of the parallel transport of vectors. There is a similar interpretation

of curvature on principal bundles. We ﬁrst show that (X, Y ) yields the vertical

component of the Lie bracket [X, Y ]of horizontal vectors X, Y ∈ H

P. It follows

from ω(X) = ω(Y ) = 0that

ω(X, Y ) = X ω(Y ) − Y ω(X) − ω([X, Y ]) =−ω([X, Y ]).

Since X

= X , Y

= Y ,wehave

(X, Y ) = d

ω(X, Y ) =−ω([X, Y ]). (10.33)

Let us consider a coordinate system {x

} on a chart U .LetV = ∂/∂x

and

W = ∂/∂x

. Take an inﬁnitesimal parallelogram γ whose corners are O =

{0, 0,...,0},P={ε, 0,...,0},Q={ε, δ, 0,...,0} and R ={0,δ,0,...,0}.

Consider the horizontal lift ˜γ of γ .LetX, Y ∈ H

P such that π

∗

X = εV and

∗

Y = δW .Then

∗

([X, Y ]

) = δ[V , W ]=δ



∂

∂x

∂

∂x



= 0 (10.34)

that is [X, Y ] is vertical. This consideration shows that the horizontal lift ˜γ of

a loop γ fails to close. This failure is proportional to the vertical vector [X, Y ]

connecting the initial point and the ﬁnal point on the same ﬁbre. The curvature

measures this distance,

(X, Y ) =−ω([X, Y ]) = A (10.35)

where A is an element of

such that [X, Y ]=A

Since the discrepancy between the initial and ﬁnal points of the horizontal

lift of a closed curve is simply the holonomy, we expect that the holonomy group

is expressed in terms of the curvature.

Theorem 10.4. (Ambrose–Singer theorem)LetP(M, G) be a G bundle over a

connected manifold M.TheLiealgebra

of the holonomy group 

of a point

∈ P agrees with the subalgebra of spanned by the elements of the form



(X, Y ) X, Y ∈ H

P (10.36)

where a ∈ P is a point on the same horizontal lift as u

. [See Choquet-Bruhat et

al (1982) for the proof.]

10.3.4 Local form of the curvature

The local form

of the curvature  is deﬁned by

≡ σ

∗

 (10.37)

where σ is a local section deﬁned on a chart U of M (cf

= σ

∗

ω). is expressed

in terms of the gauge potential

= d + ∧ (10.38a)

where d is the exterior derivative on M. The action of

on the vectors of TM is

given by

(X, Y ) = d (X, Y ) +[ (X), (Y )].(10.38b)

To prove (10.38a) we note that

= σ

∗

ω, σ

∗

ω = dσ

∗

ω and σ

∗

(ζ ∧ η) =

∗

ζ ∧ σ

∗

η. From Cartan’s structure equation, we ﬁnd

= σ

∗

ω + ω ∧ ω) = dσ

∗

ω + σ

∗

ω ∧ σ

∗

ω = d + ∧ .

Next, we ﬁnd the component expression of

on a chart U whose coordinates

are x

= ϕ(p).Let =

be the gauge potential. If we write

µν

∧ dx

, a direct computation yields

µν

= ∂

µ ν

− ∂

ν µ

]. (10.39)

is also called the curvature two-form and is identiﬁed with the (Yang–Mills)

ﬁeld strength. To avoid confusion, we call  the curvature and

the (Yang–

Mills) ﬁeld strength. Since

and

µν

are -valued functions, they can be

expanded in terms of the basis {T

} of as

= A

α µν

= F

µν

. (10.40)

The basis vectors satisfy the usual commutation relations [T

, T

]= f

αβ

.We

then obtain the well-known expression

µν

= ∂

− ∂

+ f

βγ

. (10.41)

Theorem 10.5. Let U

and U

be overlapping charts of M and let

and

ﬁeld strengths on the respective charts. On U

∩U

, they satisfy the compatibility

condition,

= Ad

−1

= t

−1

(10.42)

where t

is the transition function on U

∩U

Proof. Introduce the corresponding gauge potentials

and

= d

∧

i j

= d

∧

Substituting

= t

−1

+ t

−1

into

,weverifythat

= d (t

−1

+ t

−1

)

+ (t

−1

+ t

−1

) ∧ (t

−1

+ t

−1

)

=[−t

−1

∧ t

−1

+ t

−1

− t

−1

∧ dt

− t

−1

∧ dt

]

+[t

−1

∧

+ t

−1

∧ dt

+ t

−1

∧

+ t

−1

∧ t

−1

]

= t

−1

∧

= t

−1

where use has been made of the identity dt

−1

=−t

−1

dtt

−1

Exercise 10.7. The gauge potential is called a pure gauge if is written locally

= g

−1

dg. Show that the ﬁeld strength vanishes for a pure gauge . [It

can be shown that the converse is also true. If

= 0onachartU, the gauge

potential may be expressed locally as

= g

−1

dg.]

10.3.5 The Bianchi identity

Since ω and  are

-valued, we expand them in terms of the basis {T

} of as

ω = ω

,  = 

. Then (10.32b) becomes



= d

+ f

βγ

∧ ω

. (10.43)

Exterior differentiation of (10.43) yields



= f

βγ

∧ ω

+ f

βγ

∧ d

. (10.44)

If we note that ω(X) = 0 for a horizontal vector X,weﬁnd

D(X, Y, Z) = d

(X

, Y

, Z

) = 0

where X, Y, Z ∈ T

P. Thus, we have proved the Bianchi identity

D = 0. (10.45)

Let us ﬁnd the local form of the Bianchi identity. Operating with σ

∗

(10.44), we ﬁnd that σ

∗

 = d ·σ

∗

 = d for the LHS and

∗

ω ∧ ω − ω ∧ d

ω) = dσ

∗

ω ∧ σ

∗

ω − σ

∗

ω ∧ dσ

∗

= d

∧ − ∧ d = ∧ − ∧

for the RHS. Thus, we have obtained that

= d + ∧ − ∧ = d +[ , ]=0 (10.46)

where the action of

on a -valued p-form η on M is deﬁned by

η ≡ dη +[ ,η]. (10.47)

Note that

= d for G = U(1).

10.4 The covariant derivative on associated vector bundles

A connection one-form ω on a principal bundle P(M, G) enables us to deﬁne the

covariant derivative in associated bundles of P in a natural way.

10.4.1 The covariant derivative on associated bundles

In physics, we often need to differentiate sections of a vector bundle which is

associated with a certain principal bundle. For example, a charged scalar ﬁeld in

QED is regarded as a section of a complex line bundle associated with a U(1)

bundle P(M, U(1)). Differentiating sections covariantly is very important in

constructing gauge-invariant actions.

Let P(M, G) be a G bundle with the projection π

. Let us take a chart U

M and a section σ

over U

. We take the canonical trivialization φ

( p, e) = σ

( p).

Let ˜γ be a horizontal lift of a curve γ :[0, 1]→U

. We denote γ(0) = p

and ˜γ(0) = u

. Associated with P is a vector bundle E = P ×

V with the

projection π

, see section 9.4. Let X ∈ T

M be a tangent vector to γ(t) at p

Let s ∈ (M, E) be a section, or a vector ﬁeld, on M. Write an element of E as

[(u,v)]={(ug,ρ(g)

−1

v|u ∈ P,v ∈ V, g ∈ G}. Taking a representative of the

equivalence class amounts to ﬁxing the gauge. We choose the following form,

s( p) =[(σ

( p), ξ( p))] (10.48)

as a representative.

Now we deﬁne the parallel transport of a vector in E along a curve γ in M.

Of course, a naive guess ‘ξ is parallel transported if ξ(γ(t)) is constant along γ(t)’

does not make sense since this statement depends on the choice of the section

( p). We deﬁne a vector to be parallel transported if it is constant with respect to

a horizontal lift ˜γ of γ in P. In other words, a section s(γ (t)) =[( ˜γ(t), η(γ (t)))]

is parallel transported if η is constant along γ(t). This deﬁnition is intrinsic since

if ˜γ



(t) is another horizontal lift of γ , then it can be written as ˜γ



(t) =˜γ(t)a,

a ∈ G and we have (we omit ρ to simplify the notation)

[( ˜γ(t), η(t))]=[( ˜γ



(t)a

−1

,η(t))]=[( ˜γ



(t), a

−1

η(t))]

where η(t) stands for η(γ(t)). Hence, if η(t) is constant along γ(t), so is its

constant multiple a

−1

η(t).