Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.


and
λ
V
W
=
λV
λW
.
Let {e
α
} and { f
β
} be bases of F and F
respectively. Then {e
α
}∪{f
β
} is a basis
of F ⊕ F
and we find that dim(F ⊕ F
) = dim F + dim F
.] If π(u) = p and
π
(u
) = p
the projection π × π
acts on (u, u
) ∈ E × E
as
π × π
(u, u
) = ( p, p
). (9.35)
Thefibreat( p, p
) is F
p
⊕ F
p
. For example, if M = M
1
× M
2
,wehave
TM = TM
1
× TM
2
.
Let E
π
→ M and E
π
→ M be vector bundles with fibres F and F
respectively. The Whitney sum bundle E ⊕ E
is a pullback bundle of E × E
by f : M → M × M defined by f ( p) = ( p, p),
E ⊕ E
π
2
−→ E × E
<
π
1
<
π×π
M
f
−→ M × M.
(9.36)
Thus, E ⊕E
={(u, u
) ∈ E ×E
|π ×π
(u, u
) = ( p, p)}. The fibre of a Whitney
sum bundle is F ⊕ F
. (π × π
)
−1
( p) is isomorphic to π
−1
( p) ⊕ π
−1
( p) =
F
p
⊕ F
p
. In short, E ⊕ E
is a bundle over M whose fibre at p is F
p
⊕ F
p
.Let
{U
i
} be an open covering of M and {t
E
ij
} and {t
E
ij
} be the transition functions
of E and E
respectively. Then the transition function T
ij
of E ⊕ E
is a
(dim F + dim F
) ×(dim F + dim F
) matrix
T
ij
( p) =
t
E
ij
( p) 0
0 t
E
ij
( p)
(9.37)
which acts on F ⊕ F
on the left.
Example 9.6. Let E = TS
2
and E
= NS
2
defined in
3
.Takeu ∈ TS
2
and
v ∈ NS
2
whose local trivializations are φ
−1
i
(u) = ( p, V ) and ψ
−1
i
(v) = (q, W ),
respectively, where p, q ∈ S
2
, V ∈
2
and W ∈ .If(u,v) is a point of the
product bundle E × E
, we have a trivialization
i, j
= φ
i
× ψ
j
such that
−1
i, j
(u,v) = ( p, q; V , W ). (9.38a)
If, however, (u,v) ∈ E ⊕E
, u and v satisfy the stronger condition π(u) = π
(v)
(=p, say). Thus, we have
−1
i
(u,v) = ( p;V, W ). (9.38b)
The Whitney sum TS
2
⊕ NS
2
, S
2
being embedded in
3
, is a trivial bundle over
S
2
, whose fibre is isomorphic to
3
.
9.3.6 Tensor product bundles
Let E
π
−→ M and E
π
−→ M be vector bundles over M.Thetensor product
bundle E ⊗ E
is obtained by assigning the tensor product of fibres F
p
⊗ F
p
to
each point p ∈ M.If{e
α
} and { f
β
} are bases of F and F
, F ⊗ F
is spanned by
{e
α
⊗ f
β
} and, hence, dim(E ⊗ E
) = dim E × dim E
.
Let
B
r
E ≡ E ⊗···⊗E be the tensor product bundle of rE.If{e
α
} is the
basis of the fibre F of E, the fibre of
B
r
E is spanned by {e
α
1
⊗···⊗e
α
r
}.Ifwe
define ∧ by
e
α
∧ e
β
≡ e
α
⊗ e
β
− e
β
⊗ e
α
(9.39)
we have a bundle ∧
r
(E) of totally anti-symmetric tensors spanned by {e
α
1
∧
...∧ e
α
r
}. In particular,
r
(M), the space of r -forms on M, is identified with
(M,
r
(T
∗
M)).
Exercise 9.1. Let E
1
, E
2
and E
3
be vector bundles over M. Show that ⊗ is
distributive:
E
1
⊗ (E
2
⊕ E
3
) = (E
1
⊗ E
2
) ⊕ (E
1
⊗ E
3
). (9.40)
Express the transition functions of E
1
⊗ (E
2
⊕ F
3
) in terms of those of E
1
, E
2
and E
3
.
9.4 Principal bundles
9.4.1 Definitions
A principal bundle has a fibre F which is identical to the structure group G.A
principal bundle P
π
−→ M is also denoted by P(M, G) and is often called a G
bundle over M.
The transition function acts on the fibre on the left as before. In addition, we
may also define the action of G on F on the right.Letφ
i
: U
i
× G → π
−1
(U
i
)
be the local trivialization given by φ
−1
i
(u) = ( p, g
i
),whereu ∈ π
−1
(U
i
) and
p = π(u). The right action of G on π
−1
(U
i
) is defined by φ
−1
i
(ua) = ( p, g
i
a),
that is (figure 9.8),
ua = φ
i
( p, g
i
a) (9.41)
for any a ∈ G and u ∈ π
−1
( p). Since the right action commutes with the
left action, this definition is independent of the local trivializations. In fact, if
p ∈ U
i
∩U
j
,
ua = φ
j
( p, g
j
a) = φ
j
( p, t
ji
( p)g
i
a) = φ
i
( p, g
i
a).
Thus, the right multiplication is defined without reference to the local
trivializations. This is denoted by P × G → P or (u, a) → ua. Note that
π(ua) = π(u). The right action of G on π
−1
( p) is transitive since G acts on G
transitively on the right and F
p
= π
−1
( p) is diffeomorphic to G. Thus, for any
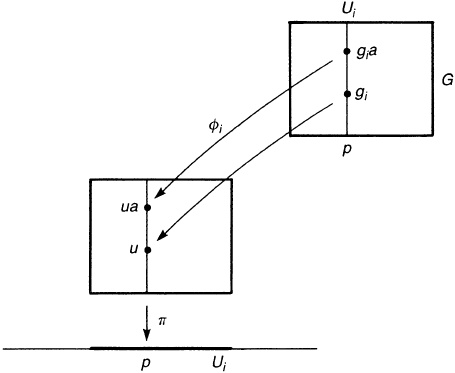
Figure 9.8. The right action of G on P.
u
1
, u
2
∈ π
−1
( p) there exists an element a of G such that u
1
= u
2
a. Then, if
π(u) = p, we can construct the whole fibre as π
−1
( p) ={ua|a ∈ G}. The action
is also free;ifua = u for some u ∈ P, a must be the unit element e of G. In fact,
if u = φ
i
( p, g
i
),wehaveφ
i
( p, g
i
a) = φ
i
( p, g
i
)a = ua = u = φ
i
( p, g
i
).Since
φ
i
is bijective, we must have g
i
a = g
i
,thatis,a = e.
Given a section s
1
( p) over U
i
, we define a preferred local trivialization
φ
i
: U
i
× G → π
−1
(U
i
) as follows. For u ∈ π
−1
( p), p ∈ U
i
,thereisaunique
element g
u
∈ G such that u = s
i
( p)g
u
. Then we define φ
i
by φ
−1
i
(u) = ( p, g
u
).
In this local trivialization, the section s
i
( p) is expressed as
s
i
( p) = φ
i
( p, e). (9.42)
This local trivialization is called the canonical local trivialization. By definition
φ
i
( p, g) = φ
i
( p, e)g = s
i
( p)g.Ifp ∈ U
i
∩U
j
, two sections s
i
( p) and s
j
( p) are
related by the transition function t
ij
( p) as follows
s
i
( p) = φ
i
( p, e) = φ
j
( p, t
ji
( p)e) = φ
j
( p, t
ji
( p))
= φ
j
( p, e)t
ji
( p) = s
j
( p)t
ji
( p). (9.43)
Example 9.7. Let P be a principal bundle with fibre U(1) = S
1
and the base
space S
2
. This principal bundle represents the topological setting of the magnetic
monopole (section 1.9). Let {U
N
, U
S
} be an open covering of S
2
, U
N
(U
S
) being
the northern (southern) hemisphere. If we parametrize S
2
by the usual polar
angles, we have
U
N
={(θ, φ)|0 ≤ θ ≤ π/2 +ε, 0 ≤ φ<2π }
U
S
={(θ, φ)|π/2 − ε ≤ θ ≤ π, 0 ≤ φ<2π}.

The intersection U
N
∩ U
S
is a strip which is essentially the equator. Let φ
N
and
φ
S
be the local trivializations such that
φ
−1
N
(u) = ( p, e
iα
N
)φ
−1
S
(u) = ( p, e
iα
S
) (9.44)
where p = π(u). Take a transition function t
NS
( p) of the form e
inφ
where n
must be an integer so that t
NS
( p) may be uniquely defined on the equator. Since
t
NS
maps the equator S
1
to U(1), this integer characterizes the homotopy group
π
1
(U(1)) = . The fibre coordinates α
N
and α
S
are related on the equator as
e
iα
N
= e
inφ
e
iα
S
. (9.45)
If n = 0, the transition function is the unit element of U(1) and we have a
trivial bundle P
0
= S
2
× S
1
.Ifn = 0, the U(1)-bundle P
n
is twisted. It is
remarkable that the topological structure of a fibre bundle is characterized by an
integer. The integer characterizes how two local sections are pasted together at
the equator. Accordingly, the integer corresponds to the element of the homotopy
group π
1
(U(1)) = .
Since U(1) is Abelian, the right action and the left action are equivalent.
Under the right action g = e
i
,wehave
φ
−1
N
(ug) = ( p, e
i(α
N
+)
) (9.46a)
φ
−1
S
(ug) = ( p, e
i(α
S
+)
). (9.46b)
The right action corresponds to the U(1)-gauge transformation.
Example 9.8. If we identify all the infinite points of the Euclidean space
m
,the
one-point compactification S
m
=
m
∪{∞}is obtained. If a trivial G bundle is
defined over
m
we shall have a new G bundle over S
m
after compactification,
which is not necessarily trivial. Let P be an SU(2) bundle over S
4
obtained from
4
by one-point compactification. This principal bundle represents an SU(2)
instanton (section 1.10). Introduce an open covering {U
N
, U
S
} of S
4
,
U
N
={(x , y, z, t)|x
2
+ y
2
+ z
2
+ t
2
≤ R
2
+ ε}
U
S
={(x , y, z, t)|R
2
− ε ≤ x
2
+ y
2
+ z
2
+ t
2
}
where R is a positive constant and ε is an infinitesimal positive number. The
thin intersection U
N
∩ U
S
is essentially S
3
.Lett
NS
( p) be the transition function
defined at p ∈ U
N
∩ U
S
.Sincet
NS
maps S
3
to SU(2), it is classified by
π
3
(SU(2)) = . The integer characterizing the bundle is called the instanton
number.Ift
NS
( p) is taken to be the unit element e ∈ SU(2),wehaveatrivial
bundle P
0
= S
3
×SU(2), which corresponds to the homotopy class 0. Non-trivial
bundles are obtained as follows. We first note that SU(2)
∼
=
S
3
(example 4.12).
An element A ∈ SU(2) is written as
A =
u v
−¯v ¯u

where |u|
2
+|v|
2
= 1. Separating u and v as u = t + iz and v = y + ix,we
find t
2
+ x
2
+ y
2
+ z
2
= 1. Thus SU(2) is regarded as the unit sphere S
3
and
π
3
(SU(2))
∼
=
π
3
(S
3
)
∼
=
classifies maps from S
3
to SU(2)
∼
=
S
3
.Theidentity
map f : S
3
→ S
3
∼
=
SU(2) is
f (x , y, z, t) →
t + izy+ ix
−y + ixt− iz
= tI
2
+ i(x σ
x
+ yσ
y
+ zσ
z
) (9.47)
where I
2
is the 2 × 2 unit matrix and the σ
µ
are the Pauli matrices. Let us take
a point p = (x, y, z, t) ∈ U
N
∩ U
S
.IfR = (x
2
+ y
2
+ z
2
+ t
2
)
1/2
denotes the
radial distance of p, the vector (x /R, y/R, z/R, t/R) has unit length. We assign
an element of SU(2) to the point p as
t
NS
( p) =
1
R
tI
2
+ i
i
x
i
σ
i
. (9.48)
Let φ
N
and φ
S
be the local trivializations,
φ
−1
N
(u) = (p, g
N
)φ
−1
S
(u) = ( p, g
S
) (9.49)
where p = π(u) and g
N
, g
S
∈ SU(2).OnU
N
∩U
S
,wehave
g
N
=
1
R
tI
2
+ i
i
x
i
σ
i
g
S
. (9.50)
While (t, x) scans S
3
once, t
NS
( p) sweeps SU(2) once, hence this bundle
corresponds to the homotopy class 1 of π
3
(SU(2)). It is not difficult to see that
the transition function corresponding to the homotopy class n is given by
t
NS
( p) =
1
R
n
t1 + i
i
x
i
σ
i
n
. (9.51)
To continue our study of monopoles and instantons, we have to introduce
connections (the gauge potentials) on the fibre bundle. We will come back to
these topics in the next chapter.
Example 9.9. Hopf has shown that S
3
is a U(1) bundle over S
2
. The unit three-
sphere embedded in
4
is expressed as
(x
1
)
2
+ (x
2
)
2
+ (x
3
)
2
+ (x
4
)
2
= 1.
If we introduce z
0
= x
1
+ ix
2
and z
1
= x
3
+ ix
4
, this becomes
|z
0
|
2
+|z
1
|
2
= 1. (9.52)

Figure 9.9. Stereographic coordinates of the sphere S
2
. (X, Y ) is defined with respect to
the projection from the North Pole while (U, V ) with respect to the projection from the
South Pole.
Let us parametrize S
2
as
(ξ
1
)
2
+ (ξ
2
)
2
+ (ξ
3
)
2
= 1.
The Hopf map π : S
3
→ S
2
is defined by
ξ
1
= 2(x
1
x
3
+ x
2
x
4
) (9.53a)
ξ
2
= 2(x
2
x
3
− x
1
x
4
) (9.53b)
ξ
3
= (x
1
)
2
+ (x
2
)
2
− (x
3
)
2
− (x
4
)
2
. (9.53c)
It is easily verified that π maps S
3
to S
2
since
(ξ
1
)
2
+ (ξ
2
)
2
+ (ξ
3
)
2
=[(x
1
)
2
+ (x
2
)
2
+ (x
3
)
2
+ (x
4
)
2
]
2
= 1.
Let (X, Y ) be the stereographic projection coordinates of a point in the
southern hemisphere U
S
of S
2
from the North Pole. If we take a complex plane
which contains the equator of S
2
, Z = X + iY is within the circle of unit radius.
We found in example 8.1 that (figure 9.9)
Z =
ξ
1
+ iξ
2
1 −ξ
3
=
x
1
+ ix
2
x
3
+ ix
4
=
z
0
z
1
(ξ ∈ U
S
). (9.54a)
Observe that Z is invariant under
(z
0
, z
1
) → (λz
0
,λz
1
)
where λ ∈ U(1).Since|λ|=1, the point (λz
0
,λz
1
) is also in S
3
.The
stereographic coordinates (U, V ) of the northern hemisphere U
N
projected from
the South Pole are given by
W = U + iV =
ξ
1
− iξ
2
1 +ξ
3
=
x
3
+ ix
4
x
1
+ ix
2
=
z
1
z
0
(ξ ∈ U
N
). (9.54b)

Note that Z = 1/W on the equator U
N
∩U
S
.
The fibre bundle structure is given as follows. We first define the local
trivializations, φ
−1
S
: π
−1
(U
S
) → U
S
× U(1) by
(z
0
, z
1
) → (z
0
/z
1
, z
1
/|z
1
|) (9.55a)
and φ
−1
N
: π
−1
(U
N
) → U
N
× U(1) by
(z
0
, z
1
) → (z
1
/z
0
, z
0
/|z
0
|). (9.55b)
Observe that these local trivializations are well defined on each chart. For
example, z
0
= 0onU
N
, hence both z
1
/z
0
= U + iV and z
0
/ |z
0
| are non-
singular. On the equator, ξ
3
= 0, we have |z
0
|=|z
1
|=1/
√
2. Accordingly, the
local trivializations on the equator are
φ
−1
S
: (z
0
, z
1
) → (z
0
/z
1
,
√
2z
1
) (9.56a)
and
φ
−1
N
: (z
0
, z
1
) → (z
1
/z
0
,
√
2z
0
). (9.56b)
The transition function on the equator is
t
NS
(ξ) =
√
2z
0
√
2z
1
= ξ
1
+ iξ
2
∈ U(1). (9.57)
If we circumnavigate the equator, t
NS
(ξ) traverses the unit circle in the complex
plane once, hence the U(1) bundle S
3
π
−→ S
2
is characterized by the homotopy
class 1 of π
1
(U(1)) = . Trautman (1977), Minami (1979) and Ryder (1980)
have pointed out that a magnetic monopole of unit strength is described by the
Hopf map S
3
π
−→ S
2
.
The Hopf map can be understood from a slightly different point of view. We
regard S
3
as a complex one-sphere
S
1
={(z
0
, z
1
) ∈
2
||z
0
|
2
+|z
1
|
2
= 1}.
Define a map π : S
1
→ P
1
by
(z
0
, z
1
) →[(z
0
, z
1
)]={λ(z
0
, z
1
)|λ ∈ −{0}}. (9.58)
Under this map, points of S
3
of the form λ(z
0
, z
1
), |λ|=1 are mapped to a single
point of
P
1
= S
2
. This is the Hopf map π : S
3
→ S
2
obtained earlier. This
is easily generalized to the case of the quaternion
. The quaternion algebra is
defined by the product table,
i
2
= j
2
= k
2
=−1 ij=−ji = k
jk =−kj= iki=−ik= j.

An arbitrary element of
is written as
q = t + ix + jy + kz.
Clearly the unit quaternion |q|=(t
2
+ x
2
+ y
2
+ z
2
)
1/2
= 1representsS
3
∼
=
SU(2). The quaternion one-sphere is given by
S
1
={(q
0
, q
1
) ∈
2
||q
0
|
2
+|q
1
|
2
= 1} (9.59)
which represents S
7
. The Hopf map, in this case, takes the form
π : S
1
→ P
1
(9.60)
where
P
1
is the quaternion projective space whose element is
[(q
0
, q
1
)]={η(q
0
, q
1
) ∈
2
|η ∈ −{0}}. (9.61)
Points of S
7
with |η|=1 are mapped under this map to a single point of
P
1
= S
4
and we have the Hopf map
π : S
7
→ S
4
. (9.62)
The fibre is the unit quaternion S
3
= SU(2). The transition function defined by
the Hopf map belongs to the class 1 of π
3
(SU(2))
∼
=
. An instanton of unit
strength is described in terms of this Hopf map.
Octonions define a Hopf map π : S
15
→ S
8
. This differs from other Hopf
maps in that the fibre S
7
is not really a group. So far we have not found an
application of this map in physics.
1
Example 9.10. Let H be a closed Lie subgroup of a Lie group G.Weshow
that G is a principal bundle with fibre H and base space M = G/H .Define
the right action of H on G by g → ga, g ∈ G, a ∈ H . The right action is
differentiable since G is a Lie group. Define the projection π : G → M = G/H
by the map π : g →[g]={gh|h ∈ H }. Clearly, g, ga ∈ G are mapped to
the same point [g] hence π(g) = π(ga)(=[g]). To define local trivializations,
we need to define a map f
i
: G → H on each chart U
i
.Lets be a local
section over U
i
and g ∈ π
−1
([g]).Definef
i
by f
i
(g) = s([g])
−1
g.Since
s([g]) is a section at [g], it is expressed as ga for some a ∈ H and accordingly,
s([g])
−1
g = a
−1
g
−1
g = a
−1
∈ H . Then we define the local trivialization
φ
i
: U
i
× H → G by
φ
−1
i
(g) = ([g], f
i
(g)). (9.63)
It is easy to see that f
i
(ga) = f
i
(g)a (a ∈ H ) hence φ
−1
i
(ga) = ( p, f
i
(g)a) is
satisfied. Useful examples are (see example 5.18)
O(n)/O(n − 1) = SO(n)/SO(n − 1) = S
n−1
(9.64)
U(n)/U(n − 1) = SU(n)/SU(n − 1) = S
2n−1
. (9.65)
1
Octonions are also known as Cayley numbers. The set of octonions is a vector space over but
not a field. The product is neither commutative nor associative. See John C Baez, The Octonions
math.RA/0105155 for a recent review.

9.4.2 Associated bundles
Given a principal fibre bundle P(M, G), we may construct an associated fibre
bundle as follows. Let G act on a manifold F on the left. Define an action of
g ∈ G on P × F by
(u, f ) → (ug, g
−1
f ) (9.66)
where u ∈ P and f ∈ F. Then the associated fibre bundle (E,π,M, G, F, P)
is an equivalence class P × F/G in which two points (u, f ) and (ug, g
−1
f ) are
identified.
Let us consider the case in which F is a k-dimensional vector space V .Letρ
be the k-dimensional representation of G.Theassociated vector bundle P ×
ρ
V
is defined by identifying the points (u,v) and (ug,ρ(g)
−1
v) of P × V ,where
u ∈ P, g ∈ G and v ∈ V . For example, associated with P(M, GL(k,
)) is a
vector bundle over M with fibre
k
. The fibre bundle structure of an associated
vector bundle E = P ×
ρ
V is given as follows. The projection π
E
: E → M is
defined by π
E
(u,v) = π(u). This projection is well defined since π(u) = π(ug)
implies π
E
(ug,ρ(g)
−1
v) = π(ug) = π
E
(u,v). The local trivialization is given
by ψ
i
: U
i
× V → π
−1
E
(U
i
). The transition function of E is given by ρ(t
ij
( p))
where t
ij
( p) is that of P.
Conversely a vector bundle naturally induces a principal bundle associated
with it. Let E
π
−→ M be a vector bundle with dim E = k (i.e. the fibre is
k
or
k
). Then E induces a principal bundle P(E) ≡ P(M, G) over M
by employing the same transition functions. The structure group G is either
GL(k,
) or GL(k, ). Explicit construction of P(E) is carried out following
the reconstruction process described in section 9.1.
Example 9.11. Associated with a tangent bundle TM over an m-dimensional
manifold M is a principal bundle called the frame bundle LM ≡
A
p∈M
L
p
M
where L
p
M is the set of frames at p. We introduce coordinates x
µ
on a chart U
i
.
The bundle T
p
M has a natural basis {∂/∂x
µ
} on U
i
. A frame u ={X
1
,...,X
m
}
at p is expressed as
X
α
= X
µ
α
∂/∂x
µ
|
p
1 ≤ α ≤ m (9.67)
where (X
µ
α
) is an element GL(m, ) so that {X
α
} are linearly independent. We
define the local trivialization φ
i
: U
i
× GL(m, ) → π
−1
(U
i
) by φ
−1
i
(u) =
( p,(X
µ
α
)). The bundle structure of LM is defined as follows.
(i) If u ={X
1
,...,X
m
} is a frame at p,wedefineπ
L
: LM → M by
π
L
(u) = p.
(ii) The action of a = (a
i
j
) ∈ GL(m, ) on the frame u ={X
1
,...,X
m
} is
given by (u, a) → ua,whereua is a new frame at p,definedby
Y
β
= X
α
a
α
β
. (9.68)
Conversely, given any frames {X
α
} and {Y
β
} there exists an element of
GL(m,
) such that (9.68) is satisfied. Thus, GL(m, ) acts on LM
transitively.
(iii) Let U
i
and U
j
be overlapping charts with the coordinates x
µ
and y
µ
,
respectively. For p ∈ U
i
∩U
j
,wehave
X
α
= X
µ
α
∂/∂x
µ
|
p
=
˜
X
µ
α
∂/∂y
µ
|
p
(9.69)
where (X
µ
α
), (
˜
X
µ
α
) ∈ GL(m, ).SinceX
µ
α
= (∂ x
µ
/∂y
ν
)
p
˜
X
µ
α
,wefind
the transition function t
L
ij
( p) to be
t
L
ij
( p) = ((∂ x
µ
/∂y
ν
)
p
) ∈ GL(m, ). (9.70)
Accordingly, given TM, we have constructed a frame bundle LM with the
same transition functions.
In general relativity, the right action corresponds to the local Lorentz
transformation while the left action corresponds to the general coordinate
transformation. It turns out that the frame bundle is the most natural framework in
which to incorporate these transformations. If {X
α
} is normalized by introducing
a metric, the matrix (X
µ
α
) becomes the vierbein and the structure group reduces
to O(m); see section 7.8.
Example 9.12. A spinor field on M is a section of a spin bundle which we now
define. Since GL(k,
) has no spinor representation, we need to introduce an
orthonormal frame bundle whose structure group is SO(k). As we mentioned in
example 4.12, SPIN(k) is the universal covering group of SO(k).[Todefineaspin
bundle, we have to check whether the SO(k) bundle lifts to a SPIN(k) bundle over
M. The obstruction to this lifting is discussed in section 11.6.]
To be specific, let us consider a spin bundle associated with the four-
dimensional Lorentz frame bundle LM,whereM is a four-dimensional Lorentz
manifold. We are interested in a frame with a definite spacetime orientation as
well as a time orientation. The structure group is then reduced to
O
+
↑
(3, 1) ≡{ ∈ O(3, 1)|det =+1,
0
0
> 0}. (9.71)
The universal covering group of O
+
↑
(3, 1) is SL(2, ), see example 5.16(c).The
homomorphism ϕ : SL(2,
) → O
+
↑
(3, 1) is a 2 : 1 map with kerϕ ={I
2
, −I
2
}.
The Weyl spinor is a section of the fibre bundle (W,π,M,
2
, SL(2, )).The
Dirac spinor is a section of
(D,π,M,
4
, SL(2, ) ⊕ SL(2, )). (9.72)
A section of W is a (1/2, 0) representation of O
+
↑
(3, 1) and a section of
(
¯
W ,π,M,
2
, SL(2, )) is a (0, 1/2) representation, see Ramond (1989) for
example. A Dirac spinor belongs to (1/2, 0) ⊕ (0, 1/2).
The general structure of the spin bundle will be worked out in section 11.6.
