Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

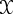
Given a ﬁbre bundle E

−→ M, the possible set of transition functions is

obviously far from unique. Let {U

} be a covering of M and {φ

} and {

} be two

sets of local trivializations giving rise to the same ﬁbre bundle. The transition

functions of respective local trivializations are

( p) = φ

−1

i, p

◦φ

j, p

(9.7a)

( p) =

−1

i, p

◦

j, p

. (9.7b)

Deﬁne a map g

( p) : F → F at each point p ∈ M by

( p) ≡ φ

−1

i, p

◦

i, p

. (9.8)

We require that g

( p) be a homeomorphism which belongs to G.This

requirement must certainly be fulﬁlled if {φ

} and {

} describe the same ﬁbre

bundle. It is easily seen from (9.7) and (9.8) that

( p) = g

( p)

−1

◦ t

( p) ◦ g

( p). (9.9)

In the practical situations which we shall encounter later, t

are the gauge

transformations required for pasting local charts together, while g

corresponds

to the gauge degrees of freedom within a chart U

. If the bundle is trivial, we may

put all the transition functions to be identity maps. Then the most general form of

the transition functions is

( p) = g

( p)

−1

( p). (9.10)

Let E

−→ M be a ﬁbre bundle. A section (or a cross section) s : M → E

is a smooth map which satisﬁes π ◦s = id

. Clearly, s( p) = s|

is an element of

= π

−1

( p). The set of sections on M is denoted by (M, F).IfU ⊂ M,we

may talk of a local section which is deﬁned only on U . (U, F) denotes the set of

local sections on U . For example, (M, TM) is identiﬁed with the set of vector

ﬁelds

(M). It should be noted that not all ﬁbre bundles admit global sections.

Example 9.1. Let E be a ﬁbre bundle E

−→ S

with a typical ﬁbre F =[−1, 1].

Let U

= (0, 2π) and U

= (−π, π) be an open covering of S

and let

A = (0,π) and B = (π, 2π) be the intersection U

∩ U

, see ﬁgure 9.3. The

local trivializations φ

and φ

are given by

−1

(u) = (θ, t), φ

−1

(u) = (θ, t)

for θ ∈ A and t ∈ F. The transition function t

(θ), θ ∈ A, is the identity map

(θ) : t → t. We have two choices on B;

(I) φ

−1

(u) = (θ, t), φ

−1

(u) = (θ, t)

(II) φ

−1

(u) = (θ, t), φ

−1

(u) = (θ, −t)

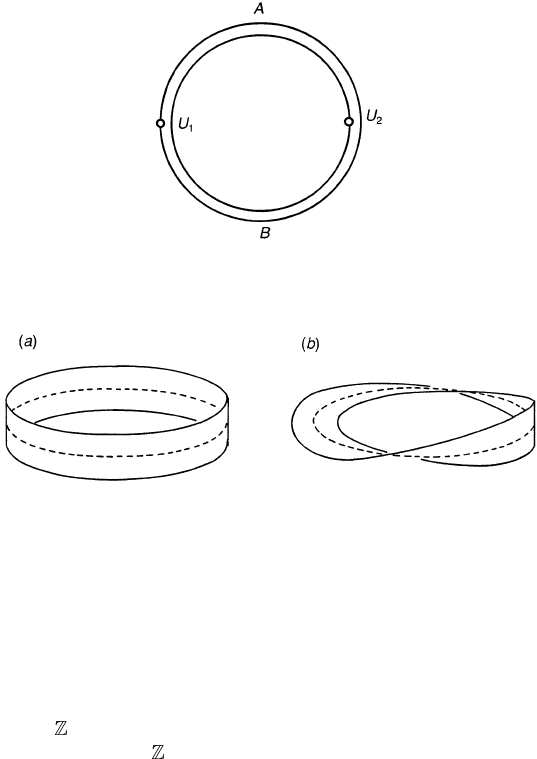
Figure 9.3. The base space S

and two charts U

and U

over which the ﬁbre bundle is

trivial.

Figure 9.4. Two ﬁbre bundles over S

:(a) is the cylinder which is a trivial bundle S

× I ;

(b)istheM¨obius strip.

For case (I), we ﬁnd that t

(θ) is the identity map and two pieces of the local

bundles are glued together to form a cylinder (ﬁgure 9.4(a)). For case (II), we

have t

(θ) : t →−t, θ ∈ B, and obtain the M¨obius strip (ﬁgure 9.4(b)). Thus, a

cylinder has the trivial structure group G ={e} where e is the identity map of F

onto F while the M¨obius strip has G ={e, g} where g : t →−t.Sinceg

= e,

we ﬁnd G

∼

. A cylinder is a trivial bundle S

× F, while the M¨obius strip is

not. [Remark: The group

is not a Lie group. This is the only occasion we use

a discrete group for the structure group.]

9.2.2 Reconstruction of ﬁbre bundles

What is the minimal information required to construct a ﬁbre bundle? We now

show that for given M, {U

}, t

( p), F and G, we can reconstruct the ﬁbre bundle

(E,π,M, F, G). This amounts to ﬁnding a unique π, E and φ

from given data.

Let us deﬁne

X ≡

× F. (9.11)

Introduce an equivalence relation ∼ between ( p, f ) ∈ U

× F and (q, f



) ∈

× F by ( p, f ) ∼ (q, f



) if and only if p = q and f



= t

( p) f .Aﬁbre

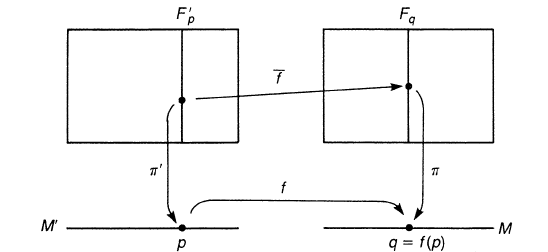
Figure 9.5. A bundle map

f : E



→ E induces a map f : M



→ M.

bundle E is then deﬁned as

E = X/ ∼ . (9.12)

Denote an element of E by [( p, f )]. The projection is given by

π :[( p, f )] → p. (9.13)

The local trivialization φ

: U

× F → π

−1

) is given by

: ( p, f ) →[( p, f )]. (9.14)

The reader should verify that E,π and {φ

} thus deﬁned satisfy all the axioms of

ﬁbre bundles. Thus, the given data reconstruct a ﬁbre bundle E uniquely.

This procedure may be employed to construct a new ﬁbre bundle from an old

one. Let (E,π,M, F, G) be a ﬁbre bundle. Associated with this bundle is a new

bundle whose base space is M, transition function t

( p), structure group G and

ﬁbre F



on which G acts. Examples of associated bundles will be given later.

9.2.3 Bundle maps

Let E

−→ M and E



−→ M



be ﬁbre bundles. A smooth map

f : E



→ E

is called a bundle map if it maps each ﬁbre F



of E



onto F

of E.Then

naturally induces a smooth map f : M



→ M such that f ( p) = q (ﬁgure 9.5).

Observe that the diagram



−→ E









−→ M







−→

f (u)







−→ q







(9.15)

commutes. [Caution: A smooth map

f : E



→ E is not necessarily a bundle

map. It may map u,v ∈ F



of E



f (u) and

f (v) on different ﬁbres of E so

that π(

f (u)) = π(

f (v)).]

Figure 9.6. Given a ﬁbre bundle E

−→ M,amap f : N → M deﬁnes a pullback bundle

∗

E over N .

9.2.4 Equivalent bundles

Two bundles E



−→ M and E

−→ M are equivalent if there exists a bundle map

f : E



→ E such that f : M → M is the identity map and

f is a diffeomorphism:



−→ E







−→ M.

(9.16)

This deﬁnition of equivalent bundles is in harmony with that given in the remarks

following deﬁnition 9.1.

9.2.5 Pullback bundles

Let E

−→ M be a ﬁbre bundle with typical ﬁbre F.Ifamapf : N → M is

given, the pair (E , f ) deﬁnes a new ﬁbre bundle over N with the same ﬁbre F

(ﬁgure 9.6). Let f

∗

E be a subspace of N × E, which consists of points ( p, u)

such that f (p) = π(u). f

∗

E ≡{( p, u) ∈ N × E| f ( p) = π(u)} is called the

pullback of E by f .TheﬁbreF

of f

∗

E is just a copy of the ﬁbre F

f ( p)

of E.If

we deﬁne f

∗

−→ N by π

: ( p, u) → p and f

∗

−→ E by ( p, u) → u,the

pullback f

∗

E may be endowed with the structure of a ﬁbre bundle and we obtain

the following bundle map,

∗

−→ E



−→ M







( p, u)

−→ u



−→ f ( p)







. (9.17)

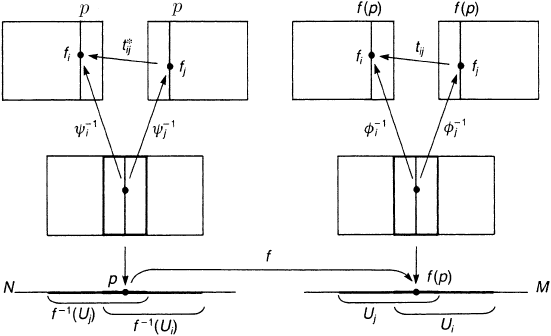
Figure 9.7. The transition function t

∗

of the pullback bundle f

∗

E is a pullback of the

transition function t

of E .

The commutativity of the diagram follows since π(π

( p, u)) = π(u) = f ( p) =

f (π

( p, u)) for ( p, u) ∈ f

∗

E. In particular, if N = M and f = id

,thentwo

ﬁbre bundles f

∗

E and E are equivalent.

Let {U

} be a covering of M and {φ

} be local trivializations. { f

−1

)}

deﬁnes a covering of N such that f

∗

E is locally trivial. Take u ∈ E such

that π(u) = f (p) ∈ U

for some p ∈ N.Ifφ

−1

(u) = ( f ( p), f

) we ﬁnd

−1

( p, u) = ( p, f

) where ψ

is the local trivialization of f

∗

E. The transition

function t

at f ( p) ∈ U

∩ U

maps f

to f

= t

( f (p)) f

. The corresponding

transition function t

∗

of f

∗

E at p ∈ f

−1

) ∩ f

−1

) also maps f

to f

;see

ﬁgure 9.7. This shows that

∗

( p) = t

( f (p)). (9.18)

Example 9.2. Let M and N be differentiable manifolds with dim M = dim N =

m.Let f : N → M be a smooth map. The map f induces a map π

: TN → TM

such that the following diagram commutes:

−→ TM



−→ M.

(9.19)

Let W = W

∂/∂y

be a vector of T

N and V = V

∂/∂x

be the corresponding

vector of T

f ( p)

M.IfTN is a pullback bundle f

∗

(TM), π

maps T

N to T

f ( p)

diffeomorphically. This is possible if and only if π

has the maximal rank m at

each point of TN.Letϕ( f (p)) = ( f

(y),..., f

(y)) be the coordinates of

f ( p) in a chart (U,ϕ)of M,wherey = ϕ(p) are the coordinates of p in a chart

(V ,ψ) of N. The maximal rank condition is given by det(∂ f

(y)/∂y

) = 0for

any p ∈ N.

9.2.6 Homotopy axiom

Let f and g be maps from M



to M. They are said to be homotopic if there

exists a smooth map F : M



×[0, 1]→M such that F ( p, 0) = f ( p) and

F( p, 1) = g( p) for any p ∈ M



, see section 4.2.

Theorem 9.1. Let E

−→ M be a ﬁbre bundle with ﬁbre F and let f and g be

homotopic maps from N to M.Thenf

∗

E and g

∗

E are equivalent bundles over

The proof is found in Steenrod (1951). Let M be a manifold which is

contractible to a point. Then there exists a homotopy F : M × I → M such

that

F( p, 0) = pF( p, 1) = p

where p

∈ M is a ﬁxed point. Let E

−→ M be a ﬁbre bundle over M and

consider pullback bundles h

∗

E and h

∗

E,whereh

( p) ≡ F( p, t).Theﬁbre

bundle h

∗

E is a pullback of a ﬁbre bundle {p

}×F and hence is a trivial bundle:

∗

E  M × F.However,h

∗

E = E since h

is the identity map. According to

theorem 9.1, h

∗

E = E is equivalent to h

∗

E = M ×F, hence E is a trivial bundle.

For example, the tangent bundle T

is trivial. We have obtained the following

corollary.

Corollary 9.1. Let E

−→ M be a ﬁbre bundle. E is trivial if M is contractible to

a point.

9.3 Vector bundles

9.3.1 Deﬁnitions and examples

A vector bundle E

−→ M is a ﬁbre bundle whose ﬁbre is a vector space. Let

F be

and M be an m-dimensional manifold. It is common to call k the

ﬁbre dimension and denote it by dim E, although the total space E is m + k

dimensional. The transition functions belong to GL(k,

), since it maps a vector

space onto another vector space of the same dimension isomorphically. If F is a

complex vector space

, the structure group is GL(k, ).

Example 9.3. A tangent bundle TM over an m-dimensional manifold M is a

vector bundle whose typical ﬁbre is

, see section 9.1. Let u be a point in

TM such that π(u) = p ∈ U

∩ U

,where{U

} covers M.Letx

= ϕ

( p)

= ϕ

( p)) be the coordinate system of U

). The vector V corresponding

to u is expressed as V = V

∂/∂x

∂/∂y

. The local trivializations are

−1

(u) = ( p, {V

})φ

−1

(u) = (p, {

}). (9.20)

The ﬁbre coordinates {V

} and {

} are related as

= G

( p)

(9.21)

where {G

( p)}={(∂ x

/∂y

)

}∈GL(m, ). Hence, a tangent bundle

is (TM,π,M,

, GL(m, )). Sections of TM are the vector ﬁelds on M;

(M) = (M, TM).

For concreteness let us work out TS

. Let the pair U

≡ S

−{South Pole}

and U

≡ S

−{North Pole} be an open covering of S

.Let(X, Y ) and (U, V )

be the respective stereographic coordinates (example 8.1). They are related as

U = X/(X

+ Y

) V =−Y/(X

+ Y

). (9.22)

Take u ∈ TS

such that π(u) = p ∈ U

∩ U

.Letφ

and φ

be the respective

local trivializations such that φ

−1

(u) = ( p, V

) and φ

−1

(u) = ( p, V

).The

transition function is

( p) =

∂(U, V )

∂(X, Y )



−cos 2θ −sin 2θ

sin 2θ −cos 2θ



(9.23)

wherewehaveputX = r cos θ and Y = r sin θ . The transition of the components

of the tangent vectors consists of a rotation of {V

} by an angle 2θ followed by a

rescaling. The reader should verify that t

( p) = t

( p)

−1

Example 9.4. Let M be an m-dimensional manifold embedded in

m+k

.Let

M be the vector space which is normal to T

M in

m+k

,thatis,U · V = 0

with respect to the Euclidean metric in

m+k

for any U ∈ N

M and V ∈ T

The vector space N

M is isomorphic to

.Thenormal bundle

NM ≡

p∈M

is a vector bundle with the typical ﬁbre

Consider the sphere S

embedded in

. The normal bundle NS

imagined as S

whose surface is pierced perpendicularly by straight lines. NS

a trivial bundle S

× .

A vector bundle whose ﬁbre is one-dimensional (F =

or ) is called a

line bundle. A cylinder S

× is a trivial -line bundle. A M¨obius strip is also a

real line bundle. The structure group GL(1,

) = −{0} or GL(1, ) = −{0}

is Abelian.

In the following, we often consider the canonical line bundle L. Recall that

an element p of

is a complex line in

n+1

through the origin (example 8.3).

The ﬁbre π

−1

( p) of L is deﬁned to be the line in

n+1

which belongs to p.More

formally, let I

n+1

≡ P

n+1

be a trivial bundle over P

. If we write an

element of I

n+1

as ( p,v), p ∈ P

,v ∈

n+1

, L is deﬁned by

L ≡{( p,v) ∈ I

n+1

|v = ap, a ∈ }.

The projection is (p,v)

→ p.

Example 9.5. The (trivial) complex line bundle L =

× is associated with

the non-relativistic quantum mechanics deﬁned on

. The wavefunction ψ(x) is

simply a section of L.

Let us consider a wavefunction ψ(x) in the ﬁeld of a magnetic monopole

studied in section 1.9. When a monopole is at the origin, ψ(x) is deﬁned on

−{0} and we have a complex line bundle over

−{0}. If we are interested

only in the wavefunction on S

surrounding the monopole, we have a complex

line bundle over S

. Note that S

is a deformation retract of

−{0}.

9.3.2 Frames

On a tangent bundle TM, each ﬁbre has a natural basis {∂/∂x

} given by the

coordinate system x

on a chart U

. We may also employ the orthonormal basis

{ˆe

} if M is endowed with a metric. ∂/∂x

or {ˆe

} is a vector ﬁeld on U

and the

set {∂/∂x

} or {ˆe

} forms linearly independent vector ﬁelds over U

.Itisalways

possible to choose m linearly independent tangent vectors over U

but it is not

necessarily the case throughout M. By deﬁnition, the components of the basis

vectors are

∂/∂x

= (0, ..., 0, 1, 0, ..., 0)

ˆe

= (0, ..., 0, 1, 0, ..., 0).

These vectors deﬁne a (local) frame over U

, see later.

Let E

→ M be a vector bundle whose ﬁbre is

(or

). On a chart

, the piece π

−1

) is trivial, π

−1

)

∼

, and we may choose k

linearly independent sections {e

( p),...,e

( p)} over U

. These sections are said

to deﬁne a frame over U

. Given a frame over U

,wehaveanaturalmapF

→ F

) given by

V = V

( p) −→ {V

}∈F. (9.24)

The local trivialization is

−1

(V ) = ( p, {V

( p)}). (9.25)

By deﬁnition, we have

( p, {0, ..., 0, 1, 0, ..., 0})

= e

( p). (9.26)

Let U

∩ U

=∅and consider the change of frames. We have a frame

( p),...,e

( p)} on U

and {˜e

( p),...,˜e

( p)} on U

,wherep ∈ U

∩ U

vector ˜e

( p) is expressed as

˜e

( p) = e

( p)G( p)

(9.27)

where G( p)

∈ GL(k, ) or GL(k, ). Any vector V ∈ π

−1

( p) is expressed as

V = V

( p) =

˜e

( p). (9.28)

From (9.27) and (9.28) we ﬁnd that

= G

−1

( p)

(9.29)

where G

−1

( p)

G( p)

= G( p)

−1

( p)

= δ

. Thus, we ﬁnd that the

transition function t

( p) is given by a matrix G

−1

( p).

9.3.3 Cotangent bundles and dual bundles

The cotangent bundle T

∗

M ≡

p∈M

∗

M is deﬁned similarly to the tangent

bundle. On a chart U

whose coordinates are x

, the basis of T

∗

M is taken to be

{dx

,...,dx

}, which is dual to {∂/∂x

}.Lety

be the coordinates of U

such

that U

∩U

=∅.Forp ∈ U

∩U

, we have the transformation,

= dx



∂y

∂x



. (9.30)

A one-form ω is expressed, in both coordinate systems, as

ω = ω

=˜ω

from which we ﬁnd that

˜ω

= G

( p)ω

(9.31)

where G

( p) ≡ (∂ x

/∂y

)

corresponds to the transition function t

( p).Note

that (M, T

∗

M) = 

(M).

This cotangent bundle is easily extended to more general cases. Given a

vector bundle E

→ M with the ﬁbre F, we may deﬁne its dual bundle E

∗

→ M.

The ﬁbre F

∗

of E

∗

is the set of linear maps of F to (or ). Given a general basis

( p)} of F

, we deﬁne the dual basis {θ

( p)} of F

∗

by θ

( p), e

( p)=δ

9.3.4 Sections of vector bundles

Let s and s



be sections of a vector bundle E

→ M. The vector addition and the

scalar multiplication are pointwisely deﬁned as

(s + s



)( p) = s( p) + s



( p) (9.32a)

( fs)( p) = f ( p)s( p) (9.32b)

where p ∈ M and f ∈

(M). The null vector 0 of each ﬁbre is left invariant

under GL(k,

) (or GL(k, )) and plays a distinguished role. Any vector bundle

E admits a global section called the null section s

∈ (M, E) such that

−1

( p)) = ( p, 0) in any local trivialization.

For example, let us consider sections of the canonical line bundle L over

.Letξ

(µ)

be the inhomogeneous coordinates and {z

} be the homogeneous

coordinates on U

. The local section s

over U

is of the form

={ξ

(µ)

,...,1,...,ξ

(µ)

}∈

n+1

The transition from one coordinate system to the other is carried out by a scalar

multiplication: s

= (z

.LetL

∗

be the dual bundle of L. Corresponding

to s

, we may choose a dual section s

∗

such that s

∗

) = 1. From this, we ﬁnd

that the transition function of s

∗

is a multiplication by z

, s

∗

= (z

∗

Aﬁbremetrich

µν

( p) is also deﬁned pointwisely. Let s and s



be sections

over U

. The inner product between s and s



at p is deﬁned by

(s, s



)

= h

µν

( p)s



( p) (9.33a)

if the ﬁbre is

.Iftheﬁbreis

we deﬁne

(s, s



)

= h

µν

( p)s



( p). (9.33b)

We have more about this subject in section 10.4.

9.3.5 The product bundle and Whitney sum bundle

Let E

→ M and E



→ M



be vector bundles with ﬁbres F and F



respectively.

The product bundle

E × E



π×π



−−−−→ M × M



(9.34)

is a ﬁbre bundle whose typical ﬁbre is F ⊕ F



. [A vector in F ⊕ F



is written as





where V ∈ F and W ∈ F



Vector addition and scalar multiplication are deﬁned by













V + V



W + W



