Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

8.7.1 Deﬁnitions

There are some differentiable manifolds which carry a similar structure to

complex manifolds. To study these manifolds, we somewhat relax the condition

(8.16) and require a weaker condition here.

Deﬁnition 8.5. Let M be a differentiable manifold. The pair (M, J ),orsimply

M, is called an almost complex manifold if there exists a tensor ﬁeld J of type

(1, 1) such that at each point p of M, J

=−id

. The tensor ﬁeld J is also

called the almost complex structure.

Since J

=−id

, J

has eigenvalues ±i. If there are m + i, then there

must be an equal number of −i, hence J

is a 2m × 2m matrix and J

=−I

Thus, M is an even-dimensional manifold. Note that not all even-dimensional

manifolds are almost complex manifolds. For example, S

is not an almost

complex manifold (Steenrod 1951). Note also that we now require a weaker

condition J

=−I

. Of course, the tensor J

deﬁned by (8.16) satisﬁes

=−I

, hence a complex manifold is an almost complex manifold. There

are almost complex manifolds which are not complex manifolds. For example, it

is known that S

admits an almost complex structure, although it is not a complex

manifold (Fr¨ohlicher 1955).

Let us complexify a tangent space of an almost complex manifold (M, J ).

Given a linear transformation J

at T

M such that J

=−I

,weextendJ

to a

-linear map deﬁned on T

M . J

deﬁned on T

M also satisﬁes J

=−I

(X + iY ) = J

X + i J

Y =−X + i(−Y ) =−(X + iY )

where X, Y ∈ T

M. Let us divide T

M into two disjoint vector subspaces,

according to the eigenvalue of J

M = T

⊕ T

−

(8.121)

where

={Z ∈ T

M |J

Z =±iZ}. (8.122)

Any vector V ∈ T

M is written as V = W

+ W

,whereW

, W

∈ T

Note that J

V = iW

−iW

. At this stage the reader might have noticed that we

can follow the classiﬁcation scheme of vectors and vector ﬁelds developed for the

complex manifolds in section 8.2. In fact, the only difference is that on a complex

manifold the almost complex structure is explicitly given by (8.18), while on

an almost complex manifold, it is required to satisfy the less strict condition

=−I

. To classify the complexiﬁed tangent spaces and complexiﬁed vector

spaces, we only need the latter condition. Accordingly, we separate T

M into

and (M) into (M)

, although there does not necessarily exist a basis

of T

of the form {∂/∂z

}. For example, we may still deﬁne the projection

operators

≡

(id

∓ i J

) : T

M → T

. (8.123)

We call a vector in T

−

) a holomorphic (anti-holomorphic) vector and

a vector ﬁeld in

(M)

( (M)

−

) a holomorphic (anti-holomorphic) vector ﬁeld.

Deﬁnition 8.6. Let (M, J ) be an almost complex manifold. lf the Lie bracket of

any holomorphic vector ﬁelds X, Y ∈

(M) is again a holomorphic vector ﬁeld,

[X, Y ]∈

(M), the almost complex structure J is said to be integrable.

Let (M, J ) be an almost complex manifold. Deﬁne the Nijenhuis tensor

ﬁeld N :

(M) × (M) → (M) by

N(X, Y ) ≡[X, Y ]+J[JX, Y ]+J[X, JY]−[JX, JY]. (8.124)

Given a basis {e

= ∂/∂x

} and the dual basis {dx

}, the almost complex

structure is expressed as J = J

⊗ ∂/∂x

. The component expression

of N is

N(X, Y ) = (X

∂

− Y

∂

+ J

∂

− Y

∂

)}e

+ J

∂

) − J

∂

−{J

∂

) − J

∂

)}e

= X

[−J

(∂

) + J

(∂

)

− J

(∂

) + J

(∂

)]e

. (8.125)

Thus, N is indeed linear in X and Y and hence a tensor. If J is a complex

structure, J is given by (8.18) and the Nijenhuis tensor ﬁeld trivially vanishes.

Theorem 8.12. An almost complex structure J on a manifold M is integrable if

and only if N(A, B) = 0foranyA, B ∈

(M).

Proof.LetZ = X +iY , W = U +iV ∈

(M) . We extend the Nijenhuis tensor

ﬁeld so that its action on vector ﬁelds in

(M) is given by

N(Z , W ) =[Z, W ]+J [JZ, W ]+J [Z , JW]−[JZ, JW]

={N (X, U ) − N(Y, V )}+i{N(X, V ) + N(Y, U )}. (8.126)

Suppose that N(A, B) = 0foranyA, B ∈

(M). From (8.126), it turns

out that N(Z , W ) = 0forZ , W ∈

(M).LetZ , W ∈

(M) ⊂ (M) .

Since JZ = iZ and JW = iW ,wehaveN(Z , W ) = 2{[Z , W ]+iJ [Z , W ]}.By

assumption, N(Z, W ) = 0andweﬁnd[Z , W ]=−iJ [Z, W ] or J [Z , W ]=

i[Z , W ],thatis,[Z, W ]∈

(M). Thus, the almost complex structure is

integrable.

Conversely, suppose that J is integrable. Since

(M) is a direct sum of

(M) and

−

(M), we can separate Z, W ∈ (M) as Z = Z

+ Z

−

and

W = W

+ W

−

.Then

N(Z , W ) = N(Z

, W

) + N(Z

, W

−

) + N(Z

−

, W

) + N(Z

−

, W

−

Since JZ

=±iZ

and JW

=±iW

, it is easy to see that N(Z

, W

−

) =

N(Z

−

, W

) = 0. We also have

N(Z

, W

) =[Z

, W

]+J [iZ

, W

]+J [Z

, iW

]−[iZ

, iW

]

= 2[Z

, W

]−2[Z

, W

]=0

since J [Z

, W

]=i[Z

, W

]. Similarly, N(Z

−

, W

−

) vanishes and we have

shown that N(Z, W ) = 0foranyZ , W ∈

(M). In particular, it should vanish

for Z , W ∈

(M).

If M is a complex manifold, the complex structure J is a constant tensor

ﬁeld and the Nijenhuis tensor ﬁeld vanishes. What about the converse? We now

state an important (and difﬁcult to prove) theorem.

Theorem 8.13. (Newlander and Nirenberg 1957) Let (M, J ) be a 2m-dimensional

almost complex manifold. If J is integrable, the manifold M is a complex

manifold with the almost complex structure J .

In summary we have:

Integrable almost

complex structure

Vanishing Nijenhuis

tensor ﬁeld

= Complex manifold.

8.8 Orbifolds

Let M be a manifold and let G be a discrete group which acts on M. Then the

quotient space  ≡ M/G is called an orbifold. As we will see later there are

ﬁxed points in M, which do not transform under the action of G. These points

are singular and the orbifold is not a manifold in general. Thus, even though we

start with a simple manifold M, the orbifold M/G may have quite a complicated

topology.

8.8.1 One-dimensional examples

To obtain a concrete idea, let us consider a simple example. Take M =

which

is to be identiﬁed with the complex plane

.LetustakeG =

and identify

the points z,e

2πi/3

z and e

4πi/3

z. The orbifold M/G consists of a third of the

Figure 8.6. The orbifold /

is a third of the complex plane. The edges of the orbifold

are identiﬁed as shown in the ﬁgure. V becomes a vector

V after parallel transportation

along C. The angle between V and

V is 2π/3.

complex plane and after the identiﬁcation of the edges we end up with a cone,

see ﬁgure 8.6. It is interesting to see what the holonomy group of this orbifold

is. We use the ﬂat connection induced by the Euclidean metric of

. Then, after

the parallel transport of a vector V along the loop C (this is indeed a loop!), we

obtain a vector

V which is different from V after the identiﬁcation. Observe that

the angle between V and

V is 2π/3. It is easy to verify that the holomony group

. Since the holonomy is trivial for the loop C

which does not encircle the

origin, we ﬁnd that the curvature is singular at the origin (recall that the curvature

measures the non-triviality of the holonomy, see section 7.3). In general the ﬁxed

points (the origin in the present case) are singular points of the curvature. Note,

however, that

is a manifold since it has an open covering homeomorphic to

A less trivial example is obtained by taking the torus as the manifold. We

identify the points z and z + m + ne

iπ/3

(m, n ∈ ) in the complex plane; see

ﬁgure 8.7(a). If we identify the edges of the parallelogram OPQR, we have the

torus T

.Let

act on T

as α : z → e

2πi/3

z. We ﬁnd that there are three

inequivalent ﬁxed points z = (n/

√

3)e

πi/6

where n = 0, 1 and 2. This orbifold

 =

consists of two triangles surrounding a hollow; see ﬁgure 8.7(b).If

the ﬂat connection induced by the ﬂat metric of the torus is employed to deﬁne the

parallel transport of vectors, we ﬁnd that the holonomy around each ﬁxed point is

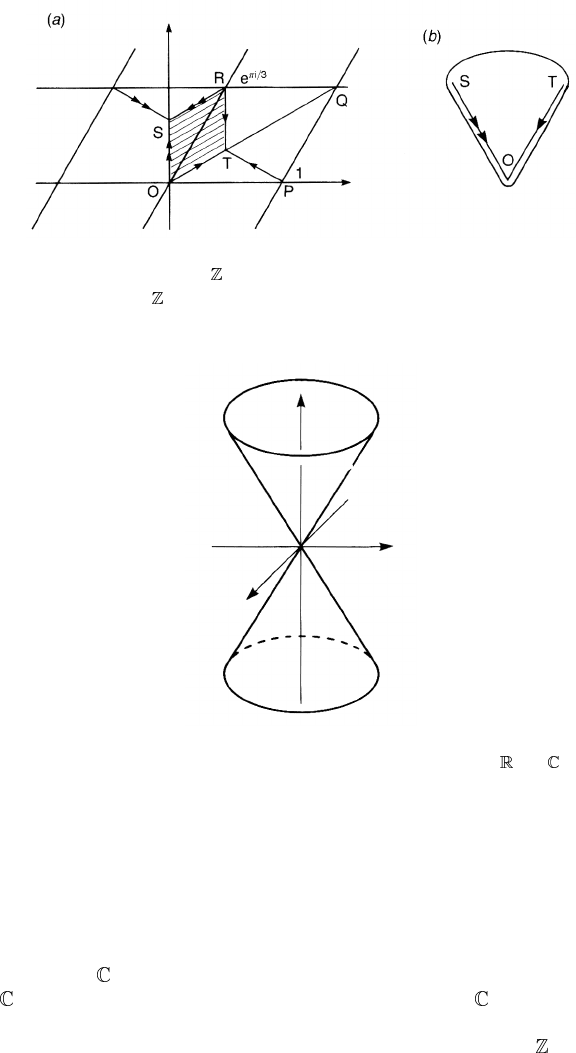
Figure 8.7. Under the action of

, points of the torus T

are identiﬁed. The shaded area

is the orbifold  = T

. If the edges of the orbifold are identiﬁed, we end up with the

object in ﬁgure 8.7(b), which is homeomorphic to the sphere S

Figure 8.8. The conical singularity. The origin does not look like

8.8.2 Three-dimensional examples

Orbifolds with three complex dimensions have been proposed as candidates for

superstring compactiﬁcation. The detailed treatment of this subject is outside the

scope of this book and the reader should consult Dixson et al (1985, 1986) and

Green et al (1987).

Let T =

/L be a three-dimensional complex torus, where L is a lattice

. For deﬁniteness, let (z

, z

) be the coordinates of

and identify z

and z

+ m + ne

πi/3

. Under this identiﬁcation, T is identiﬁed with a product of

three tori, T = T

× T

. T admits, as before, the action of

deﬁned

by α : z

→ e

2πi/3

. If each z

takes one of the values 0,(1/

√

3)e

iπ/6

(2/

√

3)e

πi/6

, the action of α leaves the point (z

) invariant. Thus, there are

= 27 ﬁxed points in the orbifold. In the present case, the ﬁxed point is a

conical singularity (ﬁgure 8.8) and the orbifold cannot be a manifold. [Remarks:

The appearance of the conical singularity can be understood more easily from a

simpler example. Let (x , y) ∈

and let

act on

as (x , y) →±(x, y).

Then the orbifold  =

has a conical singularity at the origin. In fact, let

[(x, y)]→(x

, xy, y

) ≡ (X, Y, Z ) be an embedding of  in

. Note that X, Y

and Z satisfy a relation Y

= XZ.IfX, Y and Z are thought of as real variables,

this is simply the equation of a cone.]

FIBRE BUNDLES

A manifold is a topological space which looks locally like

, but not necessarily

so globally. By introducing a chart, we give a local Euclidean structure to a

manifold, which enables us to use the conventional calculus of several variables.

A ﬁbre bundle is, so to speak, a topological space which looks locally like a direct

product of two topological spaces. Many theories in physics, such as general

relativity and gauge theories, are described naturally in terms of ﬁbre bundles.

Relevant references are Choquet-Bruhat et al (1982), Eguchi et al (1980) and

Nash and Sen (1983). A complete analysis is found in Kobayashi and Nomizu

(1963, 1969) and Steenrod (1951).

9.1 Tangent bundles

For clariﬁcation, we begin our exposition with a motivating example. A tangent

bundle TM over an m-dimensional manifold M is a collection of all the tangent

spaces of M:

TM ≡

p∈M

M. (9.1)

The manifold M over which TM is deﬁned is called the base space.Let{U

} be

an open covering of M.Ifx

= ϕ

( p) is the coordinate on U

, an element of

≡

p∈U

is speciﬁed by a point p ∈ M and a vector V = V

( p)(∂/∂x

∈ T

Noting that U

is homeomorphic to an open subset ϕ(U

) of

and each

M is homeomorphic to

,weﬁndthatTU

is identiﬁed with a direct

product

(ﬁgure 9.1). If ( p, V ) ∈ TU

, the identiﬁcation is given by

( p, V ) → (x

( p), V

( p)). TU

is a 2m-dimensional differentiable manifold.

What is more, TU

is decomposed into a direct product U

.Ifwepickup

a point u of TU

, we can systematically decompose the information u contains

into a point p ∈ M and a vector V ∈ T

M. Thus, we are naturally led to the

concept of projection π : TU

→ U

(ﬁgure 9.1). For any point u ∈ TU

, π(u)

is a point p ∈ U

at which the vector is deﬁned. The information about the vector

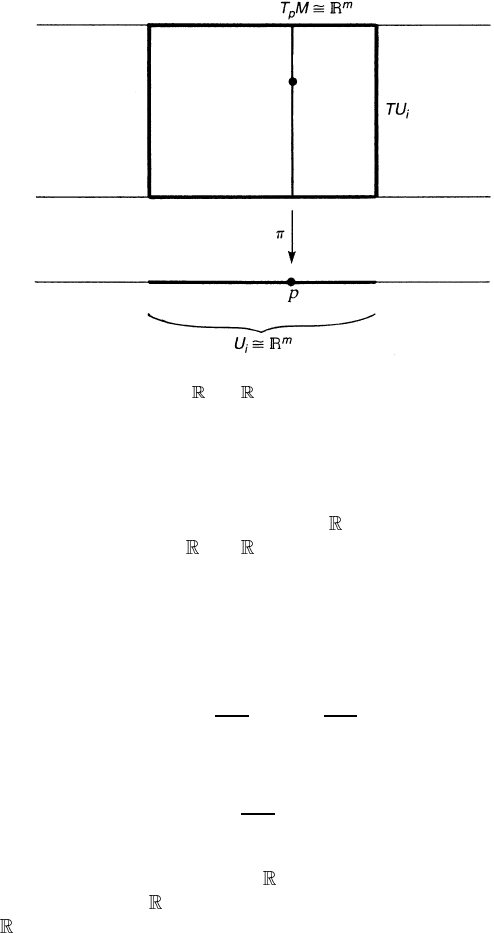
Figure 9.1. A local piece TU



of a tangent bundle TM. The projection π

projects a vector V ∈ T

M to p.

is completely lost under the projection. Observe that π

−1

( p) = T

M.Inthe

context of the theory of ﬁbre bundles, T

M is called the ﬁbre at p.

It is obvious by construction that if M =

, the tangent bundle itself is

expressed as a direct product

. However, this is not always the case

and the non-trivial structure of the tangent bundle measures the topological non-

triviality of M. To see this, we have to look not only at a single chart U

but also

at other charts. Let U

be a chart such that U

∩ U

=∅and let y

= ψ(p) be

the coordinates on U

. Take a vector V ∈ T

M where p ∈ U

∩ U

. V has two

coordinate presentations,

V = V

∂

∂x



∂

∂y



. (9.2)

It is easy to see that they are related as

∂y

∂x

( p)V

. (9.3)

For {x

} and {y

} to be good coordinate systems, the matrix (G

) ≡ (∂y

/∂x

)

must be non-singular: (G

) ∈ GL(m, ). Thus, ﬁbre coordinates are rotated

by an element of GL(m,

) whenever we change the coordinates. The group

GL(m,

) is called the structure group of TM. In this way ﬁbres are

interwoven together to form a tangent bundle, which consequently may have quite

a complicated topological structure.

We note en passant that the projection π can be deﬁned globally on M.It

is obvious that π(u) = p does not depend on a special coordinate chosen. Thus,

π : TM → M is deﬁned globally with no reference to local charts.

Let X ∈ (M) be a vector ﬁeld on M. X assigns a vector X|

∈ T

at each point p ∈ M. From our viewpoint, X is looked upon as a smooth map

M → TM. This map is not utterly arbitrary since a point p must be mapped to

a point u ∈ TM such that π(u) = p.Wedeﬁneasection (or a cross section)

of TM as a smooth map s : M → TM such that π ◦ s = id

. If a section

: U

→ TU

is deﬁned only on a chart U

, it is called a local section.

9.2 Fibre bundles

The tangent bundle in the previous section is an example of a more general

framework called a ﬁbre bundle. Deﬁnitions are now in order.

9.2.1 Deﬁnitions

Deﬁnition 9.1. A (differentiable) ﬁbre bundle (E,π,M, F, G) consists of the

following elements:

(i) A differentiable manifold E called the total space.

(ii) A differentiable manifold M called the base space.

(iii) A differentiable manifold F called the ﬁbre (or typical ﬁbre).

(iv) A surjection π : E → M called the projection. The inverse image

−1

( p) = F

∼

F is called the ﬁbre at p.

(v) A Lie group G called the structure group, which acts on F on the left.

(vi) A set of open covering {U

} of M with a diffeomorphism φ

: U

× F →

−1

) such that π ◦ φ

( p, f ) = p.Themapφ

is called the local

trivialization since φ

−1

maps π

−1

) onto the direct product U

× F .

(vii) If we write φ

( p, f ) = φ

i, p

( f ),themapφ

i, p

: F → F

is a

diffeomorphism. On U

∩ U

=∅, we require that t

( p) ≡ φ

−1

i, p

◦ φ

j, p

F → F be an element of G.Thenφ

and φ

are related by a smooth map

: U

∩U

→ G as (ﬁgure 9.2)

( p, f ) = φ

( p, t

( p) f ). (9.4)

The maps t

are called the transition functions.

[Remarks: We often use a shorthand notation E

−→ M or simply E to denote a

ﬁbre bundle (E,π,M, F, G).

Strictly speaking, the deﬁnition of a ﬁbre bundle should be independent of

the special covering {U

} of M. In the mathematical literature, this deﬁnition

is employed to deﬁne a coordinate bundle (E,π,M, F, G, {U

}, {φ

}).Two

coordinate bundles (E,π,M, F, G, {U

}, {φ

}) and (E,π,M, F, G, {V

}, {ψ

})

are said to be equivalent if (E,π,M, F, G, {U

}∪{V

}, {φ

}∪{ψ

}) is again a

coordinate bundle. A ﬁbre bundle is deﬁned as an equivalence class of coordinate

bundles. In practical applications in physics, however, we always employ a certain

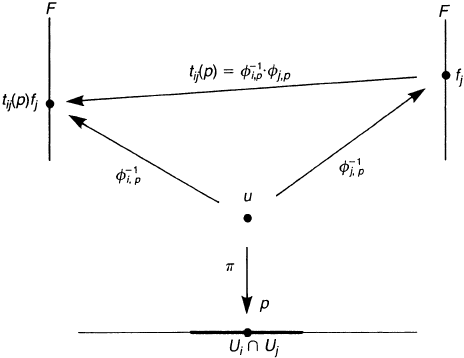
Figure 9.2. On the overlap U

∩U

, two elements f

, f

∈ F are assigned to u ∈ π

−1

( p),

p ∈ U

∩U

. They are related by t

( p) as f

= t

( p) f

deﬁnite covering and make no distinction between a coordinate bundle and a ﬁbre

bundle.]

We need to clarify several points. Let us take a chart U

of the base space M.

−1

) is a direct product diffeomorphic to U

× F, φ

−1

: π

−1

) → U

× F

being the diffeomorphism. If U

∩ U

=∅,wehavetwomapsφ

and φ

∩ U

. Let us take a point u such that π(u) = p ∈ U

∩ U

. We then assign

two elements of F, one by φ

−1

and the other by φ

−1

(u) = ( p, f

), φ

−1

(u) = ( p, f

) (9.5)

seeﬁgure9.2.Thereexistsamapt

: U

∩ U

→ G which relates f

and f

= t

( p) f

. This is also written as (9.4).

We require that the transition functions satisfy the following consistency

conditions:

( p) = identity map ( p ∈ U

) (9.6a)

( p) = t

( p)

−1

( p ∈ U

∩U

) (9.6b)

( p) ·t

( p) = t

( p)(p ∈ U

∩U

). (9.6c)

Unless these conditions are satisﬁed, local pieces of a ﬁbre bundle cannot be glued

together consistently. If all the transition functions can be taken to be identity

maps, the ﬁbre bundle is called a trivial bundle. A trivial bundle is a direct

product M × F.