Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

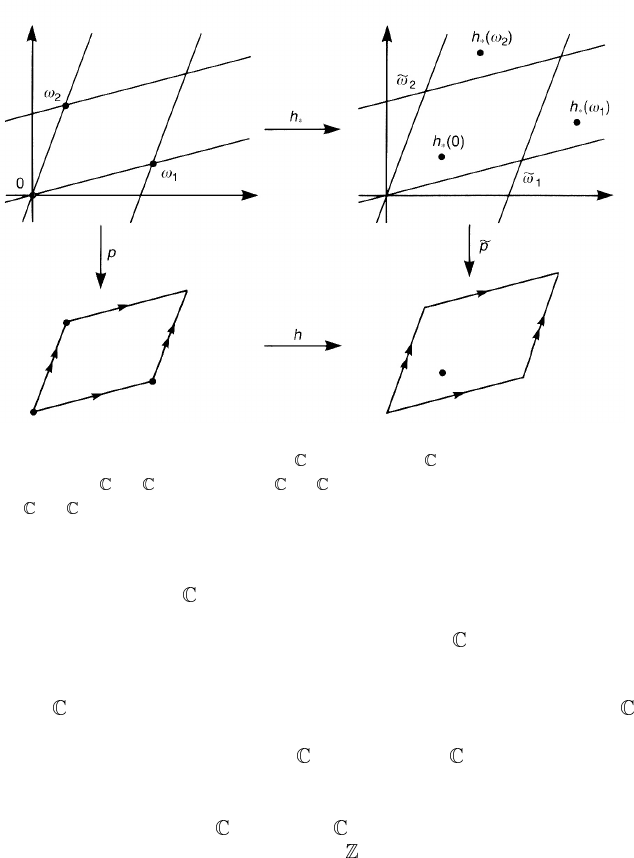
Figure 8.2. A holomorphic bijection h : /L(ω

,ω

) → /L( ˜ω

, ˜ω

) and the natural

projections p :

→ /L(ω

,ω

), ˜p : → /L( ˜ω

, ˜ω

) deﬁne a holomorphic bijection

∗

: → .

Then by analytic continuation from the origin, we obtain a one-to-one

holomorphic map h

∗

of onto itself satisfying

˜p ◦ h

∗

(z) = h ◦ p(z) for all z ∈ (8.4)

so that the diagram (8.3) commutes. It is known that a one-to-one holomorphic

map of

onto itself must be of the form z → h

∗

(z) = az + b,wherea, b ∈

and a = 0. We then have h

∗

(ω

) − h

∗

(0) = aω

and h

∗

(ω

) − h

∗

(0) = aω

For h to be well deﬁned as a map of

/L(ω

,ω

) onto /L( ˜ω

, ˜ω

),wemust

have aω

, aω

∈ L( ˜ω

, ˜ω

), see ﬁgure 8.2. By changing the roles of (ω

,ω

)

and (ω



,ω



),wehave˜a ˜ω

, ˜a ˜ω

∈ L(ω

,ω

) where ˜a = 0 is a complex number.

Hence, we conclude that if

/L(ω

,ω

), /L( ˜ω

, ˜ω

) have the same complex

structure, there must be a matrix M ∈ SL(2,

) and a complex number λ(=˜a

−1

)

such that



˜ω



= λM





. (8.5)

Conversely, we verify that (ω

,ω

) and (ω



,ω



) related by (8.5) deﬁne the same

complex structure. In fact,





and M





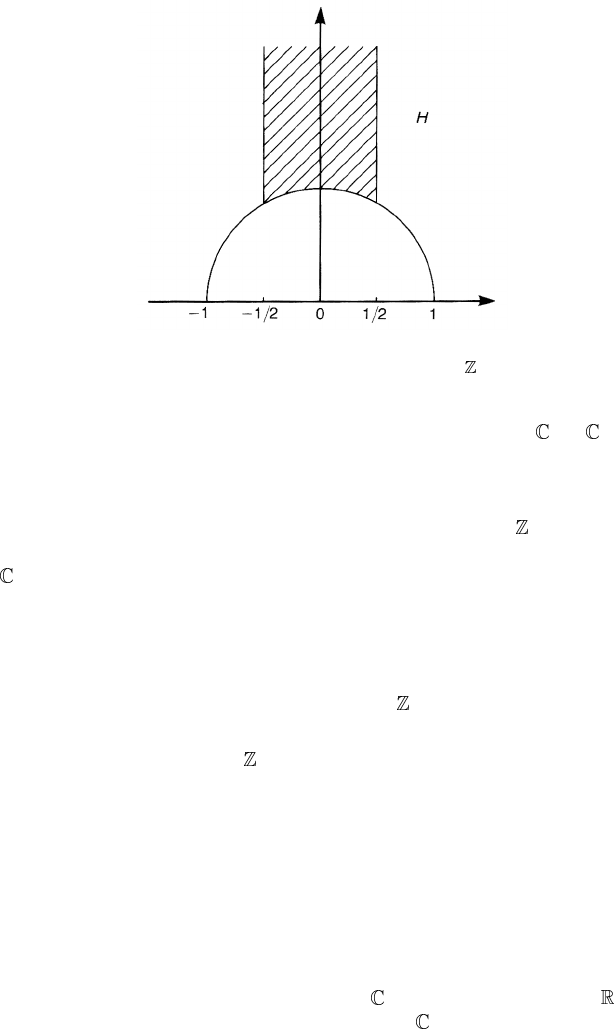
Figure 8.3. The quotient space H/PSL(2, ).

deﬁne the same lattice (modulo translation) and we may take h

∗

: → to be

z → z + b. L(ω

,ω

) and L(λω

,λω

) also deﬁne the same complex structure.

We take, in this case, h

∗

: z → λz + b.

We have shown that the complex structure on T

is deﬁned by a pair of

complex numbers (ω

,ω

) modulo a constant factor and PSL(2, ).Togetridof

the constant factor, we introduce the modular parameter τ ≡ ω

/ω

∈ H ≡{z ∈

|Im z > 0}, to specify the complex structure of T

. Without loss of generality,

we take 1 and τ to be the generators of a lattice. Note, however, that not all of

τ ∈ H are independent modular parameters. As was shown previously, τ and



= (aτ + b)/(cτ + d) deﬁne the same complex structure if





∈ PSL(2,

The quotient space H/PSL(2,

) is shown in ﬁgure 8.3, the derivation of which

can be found in Koblitz (1984) p 100, and Gunning (1962) p 4.

The change τ → τ



is called the modular transformation and is generated

by τ → τ + 1andτ →−1/τ . The transformation τ → τ + 1 generates a

Dehn twist along the meridian m as follows (ﬁgure 8.4(a)). (i) First, cut a torus

along m. (ii) Then take one of the lips of the cut and rotate it by 2π with the other

lip kept ﬁxed. (iii) Then glue the lips together again. The other transformation

τ →−1/τ corresponds to changing the roles of the longitude l and the meridian

m (ﬁgure 8.4(b)).

Example 8.3. The complex projective space

is deﬁned similarly to P

;

see example 5.4. The ntuple z = (z

,...,z

) ∈

n+1

determines a complex

line through the origin provided that z = 0. Deﬁne an equivalence relation

Figure 8.4. (a) Dehn twists generate modular transformations. (b)τ →−1/τ changes

the roles of l and m.

by z ∼ w if there exists a complex number a = 0suchthatw = az.

Then

≡ (

n+1

−{0})/ ∼.The(n + 1) numbers z

, z

,...,z

are

called the homogeneous coordinates, which is denoted by [z

, z

,...,z

]where

,...,z

) is identiﬁed with (λz

,...,λz

)(λ= 0). A chart U

is a subset of

n+1

−{0} such that z

= 0. In a chart U

,theinhomogeneous coordinates are

deﬁned by ξ

(µ)

= z

(ν = µ).InU

∩U

=∅, the coordinate transformation

µν

→

(ν)

→ ξ

(µ)

(ν)

. (8.6)

Accordingly, ψ

µν

is a multiplication by z

, which is, of course, holomorphic.

Example 8.4. The complex Grassmann manifolds G

k,n

( ) are deﬁned similarly

to the real Grassmann manifolds; see example 5.5. G

k,n

( ) is the set of complex

k-dimensional subspaces of

. Note that P

= G

1,n+1

( ).

Let M

k,n

( ) be the set of k × n matrices of rank k (k ≤ n).Take

A, B ∈ M

k,n

( ) and deﬁne an equivalence relation by A ∼ B if there exists

g ∈ GL(k,

) such that B = gA. We identify G

k,n

( ) with M

k,n

( )/GL(k, ).

Let {A

,...,A

} be the collection of all the k × k minors of A ∈ M

k,n

( ).We

deﬁne the chart U

to be a subset of G

k,n

( ) such that det A

= 0. The k(n −k)

coordinates on U

are given by the non-trivial entries of the matrix A

−1

A.See

example 5.5 for details.

Example 8.5. The common zeros of a set of homogeneous polynomials are a

compact submanifold of

called an algebraic variety. For example, let

P(z

,...,z

) be a homogeneous polynomial of degree d.Ifa = 0isacomplex

number, P satisﬁes

P(az

,...,az

) = a

P(z

,...,z

This shows that the zeros of P are deﬁned on

;ifP(z

,...,z

) = 0then

P([z

,...,z

]) = 0. For deﬁniteness, consider

P(z

, z

) = (z

)

+ (z

)

+ (z

)

and deﬁne N by

N ={[z

, z

]∈ P

|P(z

, z

) = 0}. (8.7)

We deﬁne U

as in example 8.3. In N ∩U

,wehave

[ξ

(0)

]

+[ξ

(0)

]

+ 1 = 0

where ξ

(0)

= z

(note that z

= 0). Consider a holomorphic change of

coordinates (ξ

(0)

,ξ

(0)

) → (η

= ξ

(0)

,η

=[ξ

(0)

]

+[ξ

(0)

]

+ 1). Note that

∂(η

,η

)/∂(ξ

(0)

,ξ

(0)

) = 0 unless ξ

(0)

= z

= 0. Then N ∩U

∩U

={(η

,η

) ∈

|η

= 0} is clearly a one-dimensional submanifold of

.Ifξ

(0)

= z

= 0, we

have (ξ

(0)

,ξ

(0)

) → (ζ

=[ξ

(0)

]

+[ξ

(0)

]

+1,ζ

= ξ

(0)

) for which the Jacobian

does not vanish unless ξ

(0)

= z

= 0. Then N ∩U

∩U

={(ζ

,ζ

) ∈

|ζ

0} is a one-dimensional submanifold of

.OnN ∩U

∩U

, the coordinate

change η

→ ζ

is a multiplication by z

and is, hence, holomorphic. In this

way, we may deﬁne a one-dimensional compact submanifold N of

A complex manifold is a differentiable manifold. For example,

regarded as

by the identiﬁcation z

= x

+ iy

, x

, y

∈ . Similarly,

any chart U of a complex manifold has coordinates (z

,...,z

) which may be

understood as real coordinates (x

, y

,...,x

, y

). The analytic property of the

coordinate transformation functions ensures that they are differentiable when the

manifold is regarded as a 2m-dimensional differentiable manifold.

8.2 Calculus on complex manifolds

8.2.1 Holomorphic maps

Let f : M → N, M and N being complex manifolds with dim

M = m and

dim

N = n. Take a point p in a chart (U,ϕ) of M.Let(V,ψ) be a chart of N

such that f ( p) ∈ V . If we write {z

}=ϕ(p) and {w

}=ψ( f ( p)),wehavea

map ψ ◦ f ◦ϕ

−1

→

. If each function w

(1 ≤ ν ≤ n) is a holomorphic

function of z

, f is called a holomorphic map. This deﬁnition is independent

of the special coordinates chosen. In fact, let (U



,ϕ



) be another chart such that

U ∩U



=∅and z

µ

= x

λ

+iy

λ

be the coordinates. Take a point p ∈ U ∩U



.If

= u

+ iv

is a holomorphic function with respect to z,then

∂u

∂x

λ

∂u

∂x

λ

∂u

∂y

λ

∂v

∂y

λ

∂v

∂x

∂y

λ

∂v

∂y

λ

We also ﬁn d ∂u

/∂y

λ

=−∂v

/∂x

λ

. Thus, w

is holomorphic with respect to



too. It can be shown that the holomorphic property is also independent of the

choice of chart in N.

Let M and N be complex manifolds. We say M is biholomorphic to

N if there exists a diffeomorphism f : M → N which is also holomorphic

(then f

−1

: N → M is automatically holomorphic). The map f is called a

biholomorphism.

A holomorphic function is a holomorphic map f : M →

.Thereis

a striking theorem; any holomorphic function on a compact complex manifold

is constant. This is a generalization of the maximum principle of elementary

complex analysis, see Wells (1980). The set of holomorphic functions on M

is denoted by

(M). Similarly, (U ) is the set of holomorphic functions on

U ⊂ M.

8.2.2 Complexiﬁcations

Let M be a differentiable manifold with dim

M = m.Iff : M → is

decomposed as f = g + ih where g, h ∈

(M),then f is a complex-valued

smooth function. The set of complex-valued smooth functions on M is called the

complexiﬁcation of

(M), denoted by (M) . A complexiﬁed function does

not satisfy the Cauchy–Riemann relation in general. For f = g + ih ∈

(M) ,

the complex conjugate of f is

f ≡ g − ih. f is real if and only if f = f .

Before we consider the complexiﬁcation of T

M,wedeﬁnethe

complexiﬁcation V

of a general vector space V with dim V = m.Anelement

of V

takes the form X + iY where X, Y ∈ V . The vector space V becomes

a complex vector space of complex dimension m if the addition and the scalar

multiplication by a complex number a + ib are deﬁned by

+ iY

) + (X

+ iY

) = (X

+ X

) + i(Y

+ Y

)

(a + ib)(X + iY ) = (aX − bY) + i(bX +aY)

V is a vector subspace of V

since X ∈ V and X + i0 ∈ V may be identiﬁed.

Vectors in V are said to be real. The complex conjugate of Z = X + iY is

Z = X − iY . A vector Z is real if Z = Z .

A linear operator A on V is extended to act on V

A(X + iY ) = A(X ) + iA(Y ). (8.8)

If A →

is a linear function (A ∈ V

∗

), its extension is a complex-valued

linear function on V

, A : V → . In general, any tensor deﬁned on V

and V

∗

is extended so that it is deﬁned on V and (V

∗

) . An extended tensor is

complexiﬁed as t = t

+ it

,wheret

and t

are tensors of the same type. The

conjugate of t is

t ≡ t

− it

.Ift = t, the tensor is said to be real. For example

A : V

→ is real if A(X + iY ) = A(X − iY ).

Let {e

} be a basis of V . If the basis vectors are regarded as complex

vectors, the same basis {e

} becomes a basis of V . To see this, let X = X

Y = Y

∈ V .ThenZ = X + iY is uniquely expressed as (X

+ iY

.We

ﬁnd dim

V = dim V .

Now we are ready to complexify the tangent space T

M.IfV is replaced by

M, we have the complexiﬁcation T

M of T

M, whose element is expressed

as Z = X + iY (X, Y ∈ T

M). The vector Z acts on a function f = f

+ i f

∈

(M) as

Z[ f ]=X [ f

+ i f

]+iY [ f

+ i f

]

= X [ f

]−Y [ f

]+i{X [ f

]+Y [ f

]}. (8.9)

The dual vector space T

∗

M is complexiﬁed if ω,η ∈ T

∗

M are combined as

ζ = ω + iη. The set of complexiﬁed dual vectors is denoted by (T

∗

M) .

Any tensor t is extended so that it is deﬁned on T

M and (T

∗

M) and then

complexiﬁed.

Exercise 8.1. Show that (T

∗

M) = (T

M )

∗

. From now on, we denote the

complexiﬁed dual vector space simply by T

∗

M .

Given smooth vector ﬁelds X, Y ∈

(M), we deﬁne a complex vector ﬁeld

Z = X + iY . Clearly Z |

∈ T

M . The set of complex vector ﬁelds is the

complexiﬁcation of

(M) and is denoted by (M) . The conjugate vector ﬁeld

of Z = X + iY is

Z = X − iY . Z = Z if Z ∈ (M), hence (M) ⊃ (M).

The Lie bracket of Z = X + iY , W = U + iV ∈

(M) is

[X + iY, U + iV ]={[X, U ]−[Y, V ]} +i{[X, V ]+[Y, U ]}. (8.10)

The complexiﬁcation of a tensor ﬁeld of type (p, q) is deﬁned in an obvious

manner. If ω,η ∈ 

(M), ξ ≡ ω + iη ∈ 

(M) is a complexiﬁed one-form.

8.2.3 Almost complex structure

Since a complex manifold is also a differentiable manifold, we may use the

framework developed in chapter 5. We then put appropriate constraints on

the results. Let us look at the tangent space of a complex manifold M with

dim

M = m. The tangent space T

M isspannedby2m vectors



∂

∂x

,...,

∂

∂x

;

∂

∂y

,...,

∂

∂y



(8.11)

where z

= x

+ iy

are the coordinates of p in a chart (U,ϕ). With the same

coordinates, T

∗

M is spanned by

,...,dx

;dy

,...,dy

. (8.12)

Let us deﬁne 2m vectors

∂

∂z

≡



∂

∂x

− i

∂

∂y



(8.13a)

∂

∂z

≡



∂

∂x

+ i

∂

∂y



(8.13b)

where 1 ≤ µ ≤ m. Clearly they form a basis of the 2m-dimensional (complex)

vector space T

M . Note that ∂/∂z

= ∂/∂z

. Correspondingly, 2m one-forms

≡ dx

+ idy

≡ dx

− idy

(8.14)

form the basis of T

∗

M . They are dual to (8.13),

dz

,∂/∂z

=dz

,∂/∂z

=0 (8.15a)

dz

,∂/∂z

=dz

,∂/∂z

=δ

. (8.15b)

Let M be a complex manifold and deﬁne a linear map J

: T

M → T



∂

∂x



∂

∂y



∂

∂y



=−

∂

∂x

(8.16)

is a real tensor of type (1, 1). Note that

=−id

. (8.17)

Roughly speaking, J

corresponds to the multiplication by ±i. The action of J

is independent of the chart. In fact, let (U,ϕ)and (V,ψ) be overlapping charts

with ϕ(p) = z

= x

+ iy

and ψ(p) = w

= u

+ iv

.OnU ∩ V ,the

functions z

= z

(w) satisfy the Cauchy–Riemann relations. Then we ﬁnd



∂

∂u



= J



∂x

∂u

∂

∂x

∂y

∂u

∂

∂y



∂y

∂v

∂

∂y

∂x

∂v

∂

∂x

∂

∂v

We also ﬁnd that J

∂/∂v

=−∂/∂u

. Accordingly, J

takes the form



0 −I



(8.18)

with respect to the basis (8.11), where I

is the m × m unit matrix. Since all

the components of J

are constant at any point, we may deﬁne a smooth tensor

ﬁeld J whose components at p are (8.18). The tensor ﬁeld J is called the almost

complex structure of a complex manifold M. Note that any 2m-dimensional

manifold locally admits a tensor ﬁeld J which squares to −I

.However,J may

be patched across charts and deﬁned globally only on a complex manifold. The

tensor J completely speciﬁes the complex structure.

The almost complex structure J

is extended so that it may be deﬁned on

M ,

(X + iY ) ≡ J

X + iJ

Y. (8.19)

It follows from (8.16) that

∂/∂z

= i∂/∂z

∂/∂z

=−i∂/∂z

. (8.20)

Thus, we have an expression for J

in (anti-)holomorphic bases,

= idz

⊗

∂

∂z

− idz

⊗

∂

∂z

(8.21)

whose components are given by



0 −iI



. (8.22)

Let Z ∈ T

M be a vector of the form Z = Z

∂/∂z

.ThenZ is an eigenvector

of J

; J

Z = iZ. Similarly, Z = Z

∂/∂z

satisﬁes J

Z =−iZ .Inthisway

M of a complex manifold is separated into two disjoint vector spaces,

M = T

⊕ T

−

(8.23)

where

={Z ∈ T

M |J

Z =±iZ}. (8.24)

We deﬁne the projection operators

: T

M → T

≡

∓ i J

). (8.25)

In fact, J

Z =

∓ i J

)Z =±i

Z for any Z ∈ T

M . Hence,

≡

Z ∈ T

. (8.26)

Now Z ∈ T

M is uniquely decomposed as Z = Z

+ Z

−

∈ T

is spanned by {∂/∂z

} and T

−

by {∂/∂z

}. Z ∈ T

is called a

holomorphic vector while Z ∈ T

−

is called an anti-holomorphic vector.

We readily verify that

−

= T

={Z |Z ∈ T

}. (8.27)

Note that

dim

= dim T

−

dim T

M =

dim M.

Exercise 8.2. Let (U,ϕ)and (V ,ψ)be overlapping charts on a complex manifold

M and let z

= ϕ(p) and w

= ψ(p).VerifythatX = X

∂/∂z

, expressed

in the coordinates w

, contains a holomorphic basis

∂/∂w

only. Thus, the

separation of T

M into T

is independent of charts (note that J is deﬁned

independently of charts).

Given a complexiﬁed vector ﬁeld Z ∈

(M) , we obtain a new vector ﬁeld

JZ ∈

(M) deﬁned at each point of M by JZ|

= J

· Z |

. The vector ﬁeld

Z is naturally separated as

Z = Z

+ Z

−

Z (8.28)

where Z

Z. The vector ﬁeld Z

−

) is called a holomorphic (anti-

holomorphic) vector ﬁeld. Accordingly, once J is given,

(M) is decomposed

uniquely as

(M) = (M)

⊕ (M)

−

. (8.29)

Z = Z

+ Z

−

∈ (M) is real if and only if Z

= Z

−

Exercise 8.3. Let X, Y ∈

(M)

. Show that [X, Y ]∈ (M)

. [If X, Y ∈

(M)

−

,then[X, Y ]∈ (M)

−

8.3 Complex differential forms

On a complex manifold, we deﬁne complex differential forms by which we will

discuss such topological properties as cohomology groups.

8.3.1 Complexiﬁcation of real differential forms

Let M be a differentiable manifold with dim

M = m.Taketwoq-forms

ω, η ∈ 

(M) at p and deﬁne a complex q-form ζ = ω + iη. We denote the

vector space of complex q-forms at p by 

(M) . Clearly 

(M) ⊂ 

(M) .

The conjugate of ζ is

ζ = ω − iη.Acomplexq-form ζ is real if ζ = ζ .

Exercise 8.4. Let ω ∈ 

(M) . Show that

ω(V

,...,V

) = ω(V

,...,V

) V

∈ T

M . (8.30)

Show also that

ω + η = ω +η, λω = λω and ω = ω,whereω, η ∈ 

(M) and

λ ∈

A complex q-form α deﬁned on a differentiable manifold M is a smooth

assignment of an element of 

(M) . The set of complex q-forms is denoted by



(M) .Acomplexq-form ζ is uniquely decomposed as ζ = ω + iη,where

ω, η ∈ 

(M).

The exterior product of ζ = ω + iη and ξ = ϕ + iψ is deﬁned by

ζ ∧ ξ = (ω + iη) ∧ (ϕ + iψ)

= (ω ∧ ϕ − η ∧ ψ) + i(ω ∧ ψ + η ∧ ϕ). (8.31)

The exterior derivative d acts on ζ = ω + iη as

dζ = dω + idη. (8.32)

d is a real operator:

dζ = dω − idη = dζ .

Exercise 8.5. Let ω ∈ 

(M) and ξ ∈ 

(M) . Show that

ω ∧ ξ = (−1)

ξ ∧ ω (8.33)

d(ω ∧ ξ) = dω ∧ ξ + (−1)

ω ∧ dξ. (8.34)

8.3.2 Differential forms on complex manifolds

Now we restrict ourselves to complex manifolds in which we have the

decompositions T

M = T

⊕ T

−

and (M) = (M)

⊕ (M)

−

Deﬁnition 8.2. Let M be a complex manifold with dim

M = m.Letω ∈



(M) (q ≤ 2m) and r, s be positive integers such that r + s = q.LetV

∈

M (1 ≤ i ≤ q) be vectors in either T

or T

−

.Ifω(V

,...,V

) = 0

unless r of the V

are in T

and s of the V

are in T

−

, ω is said to be of

bidegree (r, s) or simply an (r, s)-form. The set of (r, s)-forms at p is denoted by



r,s

(M).Ifan(r, s)-form is assigned smoothly at each point of M,wehavean

(r, s)-form deﬁned over M.Thesetof(r, s)-forms over M is denoted by 

r,s

(M).

Take a chart (U,ϕ)with the complex coordinates ϕ(p) = z

. Wetakethe

bases (8.13) for the tangent spaces T

. The dual bases are given by (8.14).

Note that dz

is of bidegree (1, 0) since dz

,∂/∂z

=0anddz

is of bidegree

(0, 1). With these bases, a form ω of bidegree (r, s) is written as

ω =

r!s!

...µ

...ν

∧ ...∧ dz

∧ dz

∧ ...∧ dz

. (8.35)

The set {dz

∧ ... ∧ dz

∧ dz

∧ ... ∧ dz

} is the basis of 

r,s

(M).The

components are totally anti-symmetric in the µ and ν separately. Let z

and w

be two overlapping coordinates. The reader should verify that an (r, s)-form in

the z

coordinate system is also an (r, s)-form in the w

system.

Proposition 8.1. Let M be a complex manifold of dim

M = m and ω and ξ be

complex differential forms on M.

(a) If ω ∈ 

q,r

(M) then ω ∈ 

r,q

(M).

(b) If ω ∈ 

q,r

(M) and ξ ∈ 



(M),thenω ∧ ξ ∈ 

q+q



,r+r



(M).