Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.

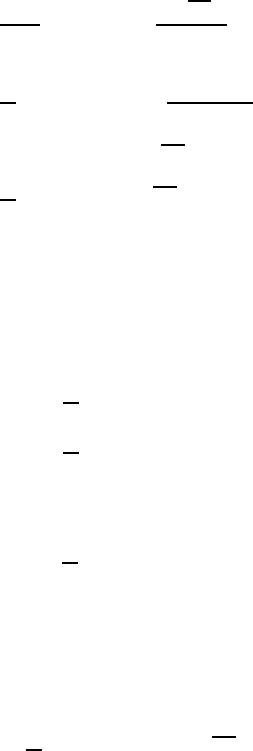
The exterior product ω ∧∗η is an m-form:
ω ∧∗η =
1
(r!)
2
ω
µ
1
...µ
r
η
ν
1
...ν
r
√
|g|
(m −r )!
ε
ν
1
...ν
r
µ
r+1
...µ
m
× dx
µ
1
∧ ...∧ dx
µ
r
∧ dx
µ
r+1
∧ ...∧ dx
µ
m
=
1
r!
µν
ω
µ
1
...µ
r
η
ν
1
...ν
r
1
r!(m −r)!
ε
ν
1
...ν
r
µ
r+1
...µ
m
× ε
µ
1
...µ
r
µ
r+1
...µ
m
|g|dx
1
∧ ...∧ dx
m
=
1
r!
ω
µ
1
...µ
r
η
µ
1
...µ
r
|g|dx
1
∧ ...∧ dx
m
. (7.178)
This expression shows that the product is symmetric:
ω ∧∗η = η ∧∗ω. (7.179)
Let {
ˆ
θ
α
} be the non-coordinate basis and
ω =
1
r!
ω
α
1
...α
r
ˆ
θ
µ
1
∧ ...∧
ˆ
θ
α
r
η =
1
r!
η
α
1
...α
r
ˆ
θ
α
1
∧ ...∧
ˆ
θ
α
r
.
Equation (7.178) is rewritten as
ω ∧∗η =
1
r!
ω
α
1
...α
r
η
α
1
...α
r
ˆ
θ
1
∧ ...∧
ˆ
θ
m
. (7.180)
Since α ∧∗β is an m-form, its integral over M is well defined. Define the
inner product (ω, η) of two r-forms by
(ω, η) ≡
ω ∧∗η
=
1
r!
M
ω
µ
1
...µ
r
η
µ
1
...µ
r
|g|dx
1
...dx
m
. (7.181)
Since ω ∧∗η = η ∧∗ω, the inner product is symmetric,
(ω, η) = (η, ω). (7.182)
If (M, g) is Riemannian, the inner product is positive definite,
(α, α) ≥ 0. (7.183)
where the equality holds only when α = 0. This is not true if (M, g) is Lorentzian.

7.9.4 Adjoints of exterior derivatives
Definition 7.6. Let d :
r−1
(M) →
r
(M) be the exterior derivative operator.
The adjoint exterior derivative operator d
†
:
r
(M) →
r−1
(M) is defined by
d
†
= (−1)
mr+m+1
∗ d∗ (7.184a)
if (M, g) is Riemannian and
d
†
= (−1)
mr+m
∗ d∗ (7.184b)
if Lorentzian, where m = dim M.
In summary, we have the following diagram (for a Riemannian manifold),
m−r
(M)
(−1)
mr+m+1
d
−−−−−−−−−−→
m−r+1
(M)
:
∗
<
∗
r
(M)
d
†
−−−−−−−−−−→
r−1
(M).
(7.185)
The operator d
†
is nilpotent since d is: d
†2
=∗d ∗∗d∗∝∗d
2
∗=0.
Theorem 7.5. Let (M, g) be a compact orientable manifold without a boundary
and α ∈
r
(M), β ∈
r−1
(M).Then
(dβ, α) = (β, d
†
α). (7.186)
Proof. Since both dβ ∧∗α and β ∧∗d
†
α are m-forms, their integrals over M are
well defined. Let d act on β ∧∗α,
d(β ∧∗α) = dβ ∧∗α − (−1)
r
β ∧ d ∗ α.
Suppose (M, g) is Riemannian. Noting that d ∗ α is an (m − r + 1)-form and
inserting the identity map (−1)
(m−r+1)[m−(m−r+1)]
∗∗=(−1)
mr+m+r+1
∗∗in
front of d ∗ α in the second term, we have
d(β ∧∗α) = dβ ∧∗α − (−1)
mr+m+1
β ∧∗(∗d ∗α).
Integrating this equation over M,wehave
M
dβ ∧∗α −
M
β ∧∗[(−1)
mr+m+1
∗ d ∗ α]=
M
d(β ∧∗α)
=
∂ M
β ∧∗α = 0
where the last equality follows by assumption. This shows that (dβ, α) =
(β, d
†
α). The reader should check how the proof is modified when (M, g) is
Lorentzian.
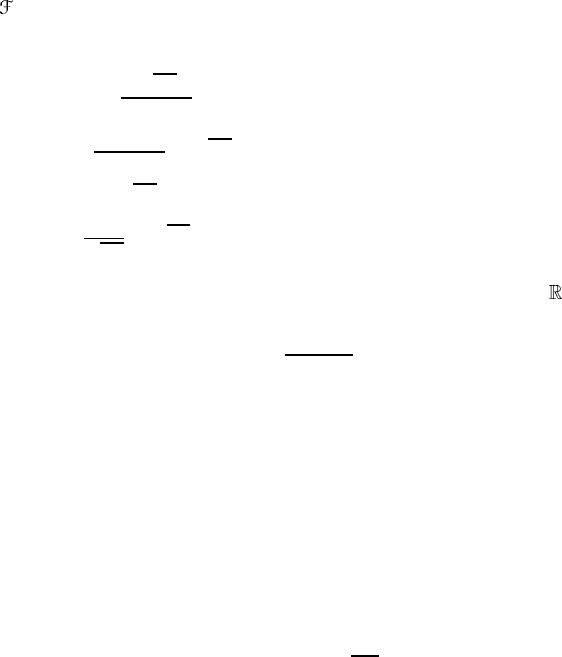
7.9.5 The Laplacian, harmonic forms and the Hodge decomposition
theorem
Definition 7.7. The Laplacian :
r
(M) →
r
(M) is defined by
= (d + d
†
)
2
= dd
†
+ d
†
d. (7.187)
As an example, we obtain the explicit form of :
0
(M) →
0
(M).Let
f ∈
(M).Sinced
†
f = 0, we have
f = d
†
d f =−∗d ∗(∂
µ
f dx
µ
)
=−∗d
√
|g|
(m − 1)!
∂
µ
fg
µλ
ε
λν
2
...ν
m
dx
ν
2
∧ ...∧ dx
ν
m
=−∗
1
(m − 1)!
∂
ν
[
|g|g
λµ
∂
µ
f ]ε
λν
2
...ν
m
dx
ν
∧ dx
ν
2
∧ ...∧ dx
ν
m
=−∗∂
ν
[
|g|g
νµ
∂
µ
f ]g
−1
dx
1
∧ ...∧ dx
m
=−
1
√
|g|
∂
ν
[
|g|g
νµ
∂
µ
f ]. (7.188)
Exercise 7.21. Take a one-form ω = ω
µ
dx
µ
in the Euclidean space (
m
,δ).
Show that
ω =−
m
µ=1
∂
2
ω
ν
∂x
µ
∂x
µ
dx
ν
.
Example 7.16. In example 5.11, it was shown that half of the Maxwell equations
are reduced to the identity, dF = d
2
A = 0, where A = A
µ
dx
µ
is the vector
potential one-form and F = dA is the electromagnetic two-form. Let ρ be the
electric charge density and j the electric current density and form the current one-
form j = η
µν
j
ν
dx
µ
=−ρ dt + j · dx. Then the remaining Maxwell equations
become
d
†
F = d
†
dA = j. (7.189a)
The component expression is
∇·E = ρ ∇×B −
∂ E
∂t
= j. (7.189b)
The vector potential A has a large number of degrees of freedom and we can
always choose an A which satisfies the Lorentz condition d
†
A = 0. Then
(7.189a) becomes (dd
†
+ d
†
d)A = A = j .
Let (M, g) be a compact Riemannian manifold. The Laplacian is a
positive operator on M in the sense that
(ω, ω) = (ω, (d
†
d + dd
†
)ω) = (dω, dω) + (d
†
ω, d
†
ω) ≥ 0 (7.190)
where (7.183) has been used. An r -form ω is called harmonic if ω = 0and
closed (coclosed)ifdω = 0 (d
†
ω = 0). The following theorem is a direct
consequence of (7.190).
Theorem 7.6. An r -form ω is harmonic if and only if ω is closed and coclosed.
An r -form ω is called coexact if it is written globally as
ω
r
= d
†
β
r+1
(7.191)
where β
r+1
∈
r+1
(M) [cf a form ω
r
∈
r
(M) is exact if ω
r
= dα
r−1
,
α
r−1
∈
r−1
(M)]. We denote the set of harmonic r-forms on M by Harm
r
(M)
and the set of exact r-forms (coexact r -forms) by d
r−1
(M)(d
†
r+1
(M)).
[Note: The set of exact r-forms has been denoted by B
r
(M) so far.]
Theorem 7.7. (Hodge decomposition theorem)Let(M, g) be a compact
orientable Riemannian manifold without a boundary. Then
r
(M) is uniquely
decomposed as
r
(M) = d
r−1
(M) ⊕d
†
r+1
(M) ⊕ Harm
r
(M). (7.192a)
[That is, any r-form ω
r
is written globally as
ω
r
= dα
r−1
+ d
†
β
r+1
+ γ
r
(7.192b)
where α
r−1
∈
r−1
(M), β
r+1
∈
r+1
(M) and γ
r
∈ Harm
r
(M).]
If r = 0, we define
−1
(M) ={0}. The proof of this theorem requires the
results of the following two easy exercises.
Exercise 7.22. Let (M, g) be as given in theorem 7.7. Show that
(dα
r−1
, d
†
β
r+1
) = (dα
r−1
,γ
r
) = (d
†
β
r+1
,γ
r
) = 0. (7.193)
Show also that if ω
r
∈
r
(M) satisfies
(dα
r−1
,ω
r
) = (d
†
β
r+1
,ω
r
) = (γ
r
,ω
r
) = 0 (7.194)
for any dα
r−1
∈ d
r−1
(M),d
†
β
r+1
∈ d
†
r+1
(M) and γ
r
∈ Harm
r
(M),then
ω
r
= 0.
Exercise 7.23. Suppose ω
r
∈
r
(M) is written as ω
r
= ψ
r
for some ψ
r
∈
r
(M). Show that (ω
r
,γ
r
) = 0foranyγ
r
∈ Harm
r
(M). The proof of the
converse ‘if ω
r
is orthogonal to any harmonic r-form, then ω
r
is written as ψ
r
for some ψ
r
∈
r
(M)’ is highly technical and we just state that the operator
−1
(the Green function) is well defined in the present problem and ψ
r
is given by
−1
ω
r
.
Let P :
r
(M) → Harm
r
(M) be a projection operator to the space of
harmonic r-forms. Take an element ω
r
∈
r
(M).Sinceω
r
− Pω
r
is orthogonal
to Harm
r
(M), it can be written as ψ
r
for some ψ
r
∈
r
(M).Thenwehave
ω
r
= d(d
†
ψ
r
) + d
†
(dψ
r
) + Pω
r
. (7.195)
This realizes the decomposition of theorem 7.7.
7.9.6 Harmonic forms and de Rham cohomology groups
We show that any element of the de Rham cohomology group has a unique
harmonic representative. Let [ω
r
]∈H
r
(M). We first show that ω
r
∈
Harm
r
(M) ⊕ d
r−1
(M). According to (7.192b), ω
r
is decomposed as ω
r
=
γ
r
+ dα
r−1
+ d
†
β
r+1
.Sincedω
r
= 0, we have
0 = (dω
r
,β
r+1
) = (dd
†
β
r+1
,β
r+1
) = (d
†
β
r+1
, d
†
β
r+1
).
This is satisfied if and only if d
†
β
r+1
= 0. Hence, ω
r
= γ
r
+dα
r−1
. From (7.195)
we have
ω
r
= Pω
r
+ d(d
†
ψ) = Pω
r
+ dd
†
−1
ω
r
. (7.196a)
γ
r
≡ Pω
r
is the harmonic representative of [ω
r
].Let(ω
r
be another representative
of [ω
r
]: (ω
r
−ω
r
= dη
r−1
, η
r−1
∈
r−1
(M). Corresponding to (7.196a), we have
(ω
r
= P(ω
r
+ d(d
†
−1
(ω
r
) = Pω
r
+ d(...) (7.196b)
where the last equality follows since dη
r−1
is orthogonal to Harm
r
(M) and hence
its projection to Harm
r
(M) vanishes. (7.196a) and (7.196b) show that [ω
r
] has a
unique harmonic representative Pω
r
.
This proof shows that H
r
(M) ⊂ Harm
r
(M). Now we prove that H
r
(M) ⊃
Harm
r
(M).Sincedγ
r
= 0foranyγ
r
∈ Harm
r
(M),wefindthatZ
r
(M) ⊃
Harm
r
(M).WealsohaveB
r
(M) ∩Harm
r
(M) =∅since B
r
(M) = d
r−1
(M),
see (7.192a). Thus, every element of Harm
r
(M) is a non-trivial member of
H
r
(M) and we find that Harm
r
(M) is a vector subspace of H
r
(M) and hence
Harm
r
(M) ⊂ H
r
(M). We have proved:
Theorem 7.8. (Hodge’s theorem) On a compact orientable Riemannian manifold
(M, g), H
r
(M) is isomorphic to Harm
r
(M):
H
r
(M)
∼
=
Harm
r
(M). (7.197)
The isomorphism is provided by identifying [ω]∈H
r
(M) with Pω ∈
Harm
r
(M).
In particular, we have
dim Harm
r
(M) = dim H
r
(M) = b
r
(7.198)
b
r
being the Betti number. The Euler characteristic is given by
χ(M) =
(−1)
r
b
r
=
(−1)
r
dim Harm
r
(M) (7.199)
see theorem 3.7. We note that the LHS is a topological quantity while the RHS is
an analytical quantity given by the eigenvalue problem of the Laplacian .

7.10 Aspects of general relativity
7.10.1 Introduction to general relativity
The general theory of relativity is one of the most beautiful and successful
theories in classical physics. There is no disagreement between the theory
and astrophysical and cosmological observations such as solar system tests,
gravitational radiation from pulsars, gravitational red shifts, the recently
discovered gravitational lens effect and so on. Readers not very familiar with
general relativity may consult Berry (1989) or the primer by Price (1982).
Einstein proposed the following principles to construct the general theory of
relativity
(I) Principle of General Relativity: All laws in physics take the same forms in
any coordinate system.
(II) Principle of Equivalence: There exists a coordinate system in which the
effect of a gravitational field vanishes locally. (An observer in a freely falling
lift does not feel gravity until it crashes.)
Any theory of gravity must reduce to Newton’s theory of gravity in the weak-
field limit. In Newton’s theory, the gravitational potential satisfies the Poisson
equation
= 4π Gρ (7.200)
where ρ is the mass density. The Einstein equation generalizes this classical result
so that the principle of general relativity is satisfied.
In general relativity, the gravitational potential is replaced by the components
of the metric tensor. Then, instead of the LHS of (7.200), we have the Einstein
tensor defined by
G
µν
≡ Ric
µν
−
1
2
g
µν
. (7.201)
Similarly, the mass density is replaced by a more general object called the
energy–momentum tensor T
µν
.TheEinstein equation takes a very similar
form to (7.200):
G
µν
= 8π GT
µν
. (7.202)
The constant 8π G is chosen so that (7.202) reproduces the Newtonian result in
the weak-field limit. The tensor T
µν
is obtained from the matter action by the
variational principle. From Noether’s theorem, T
µν
must satisfy a conservation
equation of the form ∇
µ
T
µν
= 0. A similar conservation law holds for G
µν
(but
not for Ric
µν
). We shall see in the next subsection that the LHS of (7.202) is also
obtained from the variational principle.
Exercise 7.24. Consider a metric
g
00
=−1 −
2
c
2
g
0i
= 0 g
ij
= δ
ij
1 ≤ i, j ≤ 3

and T
µν
given by T
00
= ρc
2
, T
0i
= T
ij
= 0 which corresponds to dust at
rest. Show that (7.202) reduces to the Poisson equation in the weak-field limit
(/c
2
' 1).
7.10.2 Einstein–Hilbert action
This and the next example are taken from Weinberg (1972). The general theory
of relativity describes the dynamics of the geometry, that is, the dynamics of
g
µν
. What is the action principle for this theory? As usual, we require that the
relevant action should be a scalar. Moreover, it should contain the derivatives of
g
µν
:
√
|g|d
m
x cannot describe the dynamics of the metric. The simplest guess
will be S
EH
∝
√
|g|d
m
x.Since is a scalar and
√
|g|dx
1
dx
2
...dx
m
is
the invariant volume element, S
EH
is a scalar. In the following, we show that
S
EH
indeed yields the Einstein equation under the variation with respect to the
metric. Our connection is restricted to the Levi-Civita connection. We first prove
a technical proposition.
Proposition 7.2. Let (M, g) be a (pseudo-)Riemannian manifold. Under the
variation g
µν
→ g
µν
+ δg
µν
, g
µν
, g and Ric
µν
change as
(a)δg
µν
=−g
µκ
g
λν
δg
κλ
(7.203)
(b)δg = gg
µν
δg
µν
,δ
|g|=
1
2
|g|g
µν
δg
µν
(7.204)
(c)δRic
µν
=∇
κ
δ
κ
νµ
−∇
ν
δ
κ
κµ
(Palatini identity). (7.205)
Proof.(a)Fromg
κλ
g
λν
= δ
κ
ν
, it follows that
0 = δ(g
κλ
g
λν
) = δg
κλ
g
λν
+ g
κλ
δg
λν
.
Multiplying by g
µκ
we find that δg
µν
=−g
µκ
g
λν
δg
κλ
.
(b) We first note the matrix identity ln(det g
µν
) = tr(ln g
µν
). This can be
proved by diagonalizing g
µν
. Under the variation δg
µν
, the LHS becomes δg ·g
−1
while the RHS yields g
µν
· δg
µν
, hence δg = gg
µν
δg
µν
. The rest of (7.204) is
easily derived from this.
(c) Let and
(
be two connections. The difference δ ≡
(
− is a tensor
of type (1, 2), see exercise 7.5. In the present case, we take
(
to be a connection
associated with g + δg and with g. We will work in the normal coordinate
system in which ≡ 0 (of course ∂ = 0 in general); see section 7.4. We find
δ Ric
µν
= ∂
κ
δ
κ
νµ
− ∂
ν
δ
κ
κµ
=∇
κ
δ
κ
νµ
−∇
ν
κ
κµ
.
[The reader should verify the second equality.] Since both sides are tensors, this
is valid in any coordinate system.
We define the Einstein–Hilbert action by
S
EH
≡
1
16π G
√
−g d
4
x. (7.206)
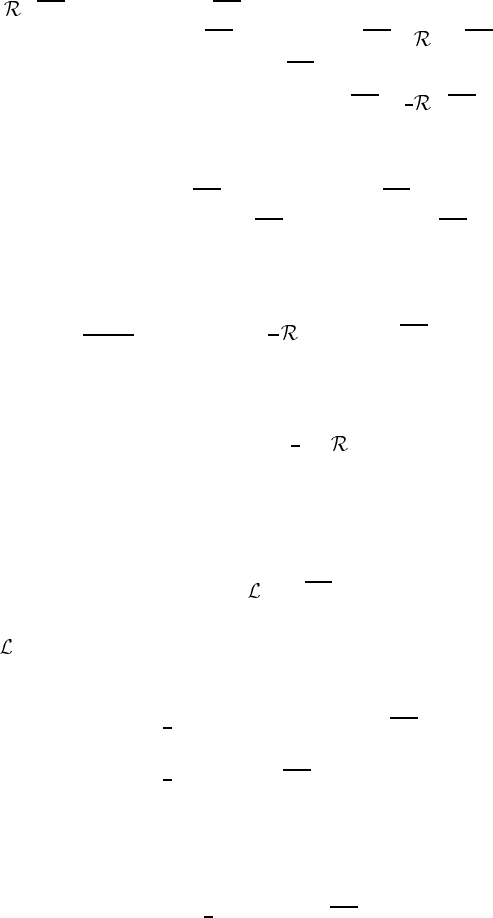
The constant factor 1/16π G is introduced to reproduce the Newtonian limit when
matter is added; see (7.214). We prove that δS
EH
= 0 leads to the vacuum Einstein
equation. Under the variation g → g + δg such that δg → 0as|x|→0, the
integrand changes as
δ(
√
−g) = δ(g
µν
Ric
µν
√
−g)
= δg
µν
Ric
µν
√
−g + g
µν
δ Ric
µν
√
−g + δ(
√
−g)
=−g
µκ
g
λν
δg
κλ
Ric
µν
√
−g
+ g
µν
(∇
κ
δ
κ
νµ
−∇
ν
κ
κµ
)
√
−g +
1
2
√
−gg
µν
δg
µν
.
We note that the second term is a total divergence,
∇
κ
(g
µν
δ
κ
νµ
√
−g) −∇
ν
(g
µν
δ
κ
κµ
√
−g)
= ∂
κ
(g
µν
δ
κ
µν
√
−g) − ∂
ν
(g
µν
δ
κ
κµ
√
−g)
and hence does not contribute to the variation. From the remaining terms we have
δS
EH
=
1
16π G
−Ric
µν
+
1
2
g
µν
δg
µν
√
−g d
4
x. (7.207)
If we require that δS
EH
= 0 under any variation δg, we obtain the vacuum Einstein
equation,
G
µν
= Ric
µν
−
1
2
g
µν
= 0 (7.208)
where the symmetric tensor G is called the Einstein tensor.
So far we have considered the gravitational field only. Suppose there exists
matter described by an action
S
M
≡
(φ)
√
−g d
4
x (7.209)
where
(φ) is the Lagrangian density of the theory. Typical examples are the real
scalar field and the Maxwell fields,
S
S
≡−
1
2
[g
µν
∂
µ
φ∂
ν
φ +m
2
φ
2
]
√
−g d
4
x (7.210a)
S
ED
≡−
1
4
F
µν
F
µν
√
−g d
4
x (7.210b)
where F
µν
= ∂
µ
A
ν
− ∂
ν
A
µ
=∇
µ
A
ν
−∇
ν
A
µ
. If the matter action changes by
δS
M
under δg,theenergy–momentum tensor T
µν
is defined by
δS
M
=
1
2
T
µν
δg
µν
√
−g d
4
x. (7.211)

Since δg
µν
is symmetric, T
µν
is also taken to be so. For example, T
µν
of a real
scalar field is given by
T
µν
(x ) = 2
1
√
−g
δ
δg
µν
(x )
S
S
= ∂
µ
φ∂
ν
φ −
1
2
g
µν
(g
κλ
∂
κ
φ∂
λ
φ +m
2
φ
2
). (7.212)
Suppose we have a gravitational field coupled with a matter field whose
action is S
M
. Now our action principle is
δ(S
EH
+ S
M
) = 0 (7.213)
under g → g + δg. From (7.207) and (7.211), we obtain the Einstein equation
G
µν
= 8π GT
µν
. (7.214)
Exercise 7.25. We may add an extra scalar to the scalar curvature without spoiling
the invariance of the action. For example, we can add a constant called the
cosmological constant ,
(
S
EH
=
1
16π G
M
( + )
√
−g d
4
x. (7.215)
Write down the vacuum Einstein equation. Other possible scalars may be such
terms as
2
, Ric
µν
Ric
µν
or R
κλµν
R
κλµν
.
7.10.3 Spinors in curved spacetime
For concreteness, we consider a Dirac spinor ψ in a four-dimensional Lorentz
manifold M. The vierbein e
α
µ
defined by
g
µν
= e
α
µ
e
β
ν
η
αβ
(7.216)
defines an orthonormal frame {
ˆ
θ
α
= e
α
µ
dx
µ
} at each point p ∈ M. As noted
before, α,β,γ,... are the local orthonormal indices while µ,ν,λ,... are the
coordinate indices. With respect to this frame, the Dirac matrices γ
α
= e
α
µ
γ
µ
satisfy {γ
α
,γ
β
}=2η
αβ
. Under a local Lorentz transformation
α
β
( p),the
Dirac spinor transforms as
ψ(p) → ρ()ψ(p)
¯
ψ(p) →
¯
ψ(p)ρ()
−1
(7.217)
where
¯
ψ ≡ ψ
†
γ
0
and ρ() is the spinor representation of . To construct an
invariant action, we seek a covariant derivative ∇
α
ψ which is a local Lorentz
vector and transforms as a spinor,
∇
α
ψ → ρ()
α
β
∇
β
ψ. (7.218)
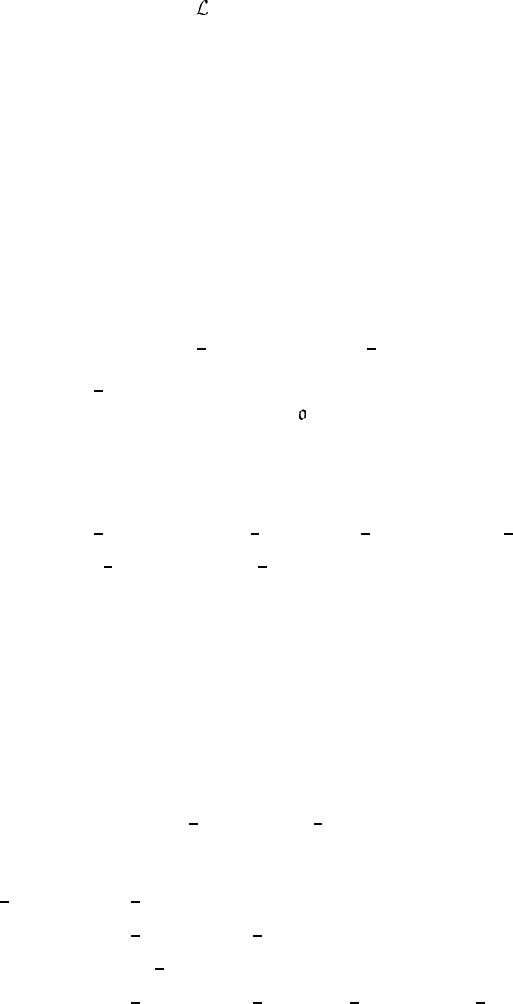
Ifwefindsucha∇
α
ψ, an invariant Lagrangian may be given by
=
¯
ψ
iγ
α
∇
α
+ m
ψ (7.219)
m being the mass of ψ. We note that e
α
µ
∂
µ
ψ transforms under (p) as
e
α
µ
∂
µ
ψ →
α
β
e
β
µ
∂
µ
ρ()ψ =
α
η
e
β
µ
[ρ()∂
µ
ψ + ∂
µ
ρ()ψ]. (7.220)
Suppose ∇
α
is of the form
∇
α
ψ = e
α
µ
[∂
µ
+
µ
]ψ. (7.221)
From (7.218) and (7.220), we find that
µ
satisfies
µ
→ ρ()
µ
ρ()
−1
− ∂
µ
ρ()ρ()
−1
. (7.222)
To find the explicit form of
µ
, we consider an infinitesimal local Lorentz
transformation
α
β
( p) = δ
α
β
+ ε
α
β
( p). The Dirac spinor transforms as
ψ → exp[
1
2
iε
αβ
αβ
]ψ [1 +
1
2
iε
αβ
αβ
]ψ (7.223)
where
αβ
≡
1
4
i
=
γ
α
,γ
β
>
is the spinor representation of the generators of the
Lorentz transformation.
αβ
satisfies the (1, 3) Lie algebra
i[
αβ
,
γδ
]=η
γβ
αδ
− η
γα
βδ
+ η
δβ
γα
− η
δα
γβ
. (7.224)
Under the same Lorentz transformation,
µ
transforms as
µ
→ (1 +
1
2
iε
αβ
αβ
)
µ
(1 −
1
2
iε
γδ
γδ
) −
1
2
i∂
µ
ε
αβ
αβ
(1 −
1
2
iε
γδ
γδ
)
=
µ
+
1
2
iε
αβ
[
αβ
,
µ
]−
1
2
i∂
µ
ε
αβ
αβ
. (7.225)
We recall that the connection one-form ω
α
β
transforms under an infinitesimal
Lorentz transformation as (see (7.152))
ω
α
β
→ ω
α
β
+ ε
α
γ
ω
γ
β
− ω
α
γ
ε
γ
β
− dε
α
β
(7.226a)
or in components,
α
µβ
→
α
µβ
+ ε
α
γ
γ
µβ
−
α
µγ
ε
γ
β
− ∂
µ
ε
α
β
. (7.226b)
From (7.224), (7.225) and (7.226b), we find that the combination
µ
≡
1
2
i
α
µ
β
αβ
=
1
2
ie
α
ν
∇
µ
e
βν
αβ
(7.227)
satisfies the transformation property (7.222). In fact,
1
2
i
α
µ
β
αβ
→
1
2
i(
α
µ
β
+ ε
α
γ
γ
µ
β
−
α
µγ
ε
γβ
− ∂
µ
ε
αβ
)
αβ
=
1
2
i
α
µ
β
αβ
+
1
2
i(ε
α
γ
γ
µ
β
αβ
−
α
µγ
ε
γβ
αβ
)
−
1
2
i∂
µ
ε
αβ
αβ
=
1
2
i
α
µ
β
αβ
+
1
2
iε
αβ
[
αβ
,
1
2
i
γ
µ
δ
γδ
]−
1
2
i∂
µ
ε
αβ
αβ
.
