Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

We assume that H ( p) acts on T

M from the right, P

X = Xh (h ∈

H ( p)). In components, this becomes P

X = X

, {e

} being the basis

of T

M. It is easy to see that H ( p) is a group. The product P



corresponds to

parallel transport along c ﬁrst and then c



. If we write P

= P



, the loop d is

given by

d(t) =



c(2t) 0 ≤ t ≤



(2t − 1)

≤ t ≤ 1.

(7.91)

The unit element corresponds to the constant map c

(t) = p (0 ≤ t ≤ 1) and

the inverse of P

is given by P

−1

,wherec

−1

(t) = c(1 − t). Note that H ( p) is

a subgroup of GL(m,

), which is the maximal holonomy group possible. H ( p)

is trivial if and only if the Riemann tensor vanishes. In particular, if (M, g) is

parallelizable (see example 7.2), we can make H ( p) trivial.

If M is (arcwise-)connected, any two points p, q ∈ M are connected by a

curve a.Thecurvea deﬁnes a map τ

: T

M → T

M by parallel transporting a

vector in T

M to T

M along a. Then the holonomy groups H ( p) and H (q) are

related by

H (q) = τ

−1

H ( p)τ

(7.92)

hence H (q) is isomorphic to H ( p).

In general, the holonomy group is a subgroup of GL(m,

).If∇ is a metric

connection, ∇ preserves the length of a vector, g

(X ), P

(X )) = g

(X, X)

for X ∈ T

M. Then the holonomy group must be a subgroup of SO(m) if (M, g)

is orientable and Riemannian and SO(m −1, 1) if it is orientable and Lorentzian.

Example 7.7. We work out the holonomy group of the Levi-Civita connection on

with the metric g = dθ ⊗ dθ + sin

dφ ⊗ dφ. The non-vanishing connection

coefﬁcients are 

φφ

=−sin θ cos θ and 

φθ

= 

θφ

= cot θ . For simplicity,

wetakeavectore

= ∂/∂θ at a point (θ

, 0) and parallel transport it along a

circle θ = θ

,0≤ φ ≤ 2π .LetX be the vector e

parallel transported along the

circle. The vector X = X

+ X

satisﬁes

∂

− sin θ

cos θ

= 0 (7.93a)

∂

+ cot θ

= 0. (7.93b)

Equations (7.93a) and (7.93b) represent the harmonic oscillations. Indeed if we

take a φ-derivative of (7.93a) and use (7.93b), we have

dφ

− sin θ

cos θ

dφ

− cos

= 0. (7.94)

The general solution is X

= A cos(C

φ) + B sin(C

φ),whereC

≡ cos θ

Since X

= 1atφ = 0wehave

= cos(C

φ) X

=−

sin(C

φ)

sin θ

After parallel transport along the circle, we end up with

X (φ = 2π) = cos(2πC

−

sin(2π C

φ)

sin θ

. (7.95)

Now the vector is rotated by ! = 2π cos θ

, with its magnitude kept ﬁxed. If we

take a point p ∈ S

and a circle in S

which passes through p, we can always ﬁnd

a coordinate system such that the circle is given by θ = θ

(0 ≤ θ<π)and we

can apply our previous calculation. The rotation angle is −2π ≤ !<2π and we

ﬁnd that the holonomy group at p ∈ S

is SO(2).

In general, S

(m ≥ 2) admits the holonomy group SO(m). Product

manifolds admit more restricted holonomy groups. The following example is

taken from Horowitz (1986). Consider six-dimensional manifolds made of the

spheres with standard metrics. Examples are S

, S

× S

, S

× S

, T

×···×S

. Their holonomy groups are:

(i) S

: H ( p) = SO(6).

(ii) S

× S

: H ( p) = SO(3) × SO(3).

(iii) S

× S

: H ( p) = SO(2) × SO(2) × SO(2).

(iv) T

: H ( p) is trivial since the Riemann tensor vanishes.

Exercise 7.14. Show that the holonomy group of the Levi-Civita connection of

the Poincar´e metric given in example 7.6 is SO(2).

7.6 Isometries and conformal transformations

7.6.1 Isometries

Deﬁnition 7.4. Let (M, g) be a (pseudo-)Riemannian manifold. A diffeomor-

phism f : M → M is an isometry if it preserves the metric

∗

f ( p)

= g

(7.96a)

that is, if g

f ( p)

( f

∗

X, f

∗

Y ) = g

(X, Y ) for X, Y ∈ T

In components, the condition (7.96a) becomes

∂y

∂x

∂y

∂x

αβ

( f (p)) = g

µν

( p)(7.96b)

where x and y are the coordinates of p and f ( p), respectively. The identity map,

the composition of the isometries and the inverse of an isometry are isometries; all

these isometries form a group. Since an isometry preserves the length of a vector,

in particular that of an inﬁnitesimal displacement vector, it may be regarded as a

rigid motion. For example, in

, the Euclidean group E

, that is the set of maps

f : x → Ax + T (A ∈ SO(n), T ∈

), is the isometry group.

7.6.2 Conformal transformations

Deﬁnition 7.5. Let (M, g) be a (pseudo-)Riemannian manifold. A diffeomor-

phism f : M → M is called a conformal transformation if it preserves the

metric uptoascale,

∗

f ( p)

= e

2σ

σ ∈ (M) (7.97a)

namely, g

f ( p)

( f

∗

X, f

∗

Y ) = e

2σ

(X, Y ) for X, Y ∈ T

In components, the condition (7.97a) becomes

∂y

∂x

∂y

∂x

αβ

( f (p)) = e

2σ(p)

µν

( p). (7.97b)

The set of conformal transformations on M is a group, the conformal group

denoted by Conf(M). Let us deﬁne the angle θ between two vectors X = X

∂

Y = Y

∂

∈ T

M by

cos θ =

(X, Y )



(X, X)g

(Y, Y )

µν



ζη

κλ

. (7.98)

If f is a conformal transformation, the angle θ



between f

∗

X and f

∗

Y is given by

cos θ



2σ

µν

2σ

ζη

· e

2σ

κλ

= cos θ

hence f preserves the angle. In other words, f changes the scale but not the

shape.

A concept related to conformal transformations is Weyl rescaling. Let g and

¯g be metrics on a manifold M. ¯g is said to be conformally related to g if

¯g

= e

2σ(p)

. (7.99)

Clearly this is an equivalence relation among the set of metrics on M.The

equivalence class is called the conformal structure. The transformation g →

2σ

g is called a Weyl rescaling. The set of Weyl rescalings on M is a group

denoted by Weyl(M).

Example 7.8. Let w = f (z) be a holomorphic function deﬁned on the complex

plane

.[AC

∞

-function regarded as a function of z = x + iy and ¯z = x − iy is

holomorphic if ∂

¯z

f (z, ¯z) = 0.] We write the real part and the imaginary part of the

respective variables as z = x + iy and w = u +iv.Themap f : (x, y) → (u,v)

is conformal since

+ dv



∂u

∂x

dx +

∂u

∂y





∂v

∂x

dx +

∂v

∂y







∂u

∂x





∂u

∂y





(dx

+ dy

) (7.100)

where use has been made of the Cauchy–Riemann relations

∂u

∂x

∂v

∂y

∂u

∂y

=−

∂v

∂x

Exercise 7.15. Let f : M → M be a conformal transformation on a Lorentz

manifold (M, g). Show that f

∗

: T

M → T

f ( p)

M preserves the local light cone

structure, namely

∗







timelike vector → timelike vector

null vector → null vector

spacelike vector → spacelike vector.

(7.101)

Let ¯g beametriconM, which is conformally related to g as ¯g = e

2σ(p)

Let us compute the Riemann tensor of ¯g. We could simply substitute ¯g into

the deﬁning equation (7.42). However, we follow the elegant coordinate-free

derivation of Nomizu (1981). Let K be the difference of the covariant derivatives

∇ with respect to ¯g and ∇ with respect to g,

K (X, Y ) ≡

∇

Y −∇

Y. (7.102)

Proposition 7.1. Let U be a vector ﬁeld which corresponds to the one-form dσ :

Z[σ ]=dσ , Z =g(U, Z ).Then

K (X, Y ) = X[σ ]Y + Y [σ ]X − g(X, Y )U. (7.103)

Proof. It follows from the torsion-free condition that K (X, Y ) = K (Y, X).Since

∇

¯g =∇

g = 0, we have

X[¯g(Y, Z )]=

∇

[¯g(Y, Z)]=¯g(

∇

, Z) +¯g(Y,

∇

and also

X[¯g(Y, Z )]=∇

2σ

g(Y, Z )]

= 2X [σ ]e

2σ

g(Y, Z ) + e

2σ

[g(∇

, Z) + g(Y, ∇

Z)].

Taking the difference between these two expressions, we have

g(K (X, Y ), Z ) + g(Y, K (X, Z)) = 2X[σ ]g(Y, Z ). (7.104a)

Permutations of (X, Y, Z ) yield

g(K (Y, X), Z ) + g(X, K (Y, Z )) = 2Y [σ ]g(X, Z ) (7.104b)

g(K (Z, X), Y ) + g(X, K (Z , Y )) = 2Z [σ ]g(X, Y ). (7.104c)

The combination (7.104a) + (7.104b) − (7.104c) yields

g(K (X, Y ), Z ) = X[σ ]g(Y, Z ) + Y [σ ]g(X, Z ) − Z [σ ]g(X, Y ). (7.105)

The last term is modiﬁed as

Z[σ ]g(X, Y ) = g(U, Z)g(X, Y ) = g(g(Y, X)U, Z).

Substituting this into (7.105), we ﬁnd

g(K (X, Y ) − X[σ ]Y − Y [σ ]X + g(X, Y )U, Z) = 0.

Since this is true for any Z , we have (7.103).

The component expression for K is

K (e

, e

) =

∇

−∇

= (



µν

− 

µν

= e

[σ ]e

+ e

[σ ]e

− g(e

, e

κλ

∂

σ e

from which it is readily seen that



µν

= 

µν

+ δ

∂

σ + δ

∂

σ − g

µν

κλ

∂

σ. (7.106)

To ﬁnd the Riemann curvature tensor, we start from the deﬁnition,

R(X, Y )Z =

∇

Z −

∇

Z −

∇

[X,Y ]

∇

[∇

Z + K (Y, Z )]−

∇

[∇

Z + K (X, Z )]

−{∇

[X,Y ]

Z + K ([X, Y ], Z )}

=∇

{∇

Z + K (Y, Z)}+K (X, ∇

Z + K (Y, Z ))

−∇

{∇

Z + K (X, Z )}−K (Y, ∇

Z + K (X, Z))

−{∇

[X,Y ]

Z + K ([X, Y ], Z )}. (7.107)

After a straightforward but tedious calculation, we ﬁnd that

R(X, Y )Z = R(X, Y )Z +∇

dσ, Z Y −∇

dσ, Z X

− g(Y, Z )∇

U + Y [σ ]Z [σ ]X

− g(Y, Z )U [σ ]X + X [σ ]g(Y, Z )U

+ g(X, Z )∇

U − X[σ ]Z[σ ]Y

+ g(X, Z )U [σ ]Y − Y [σ ]g(X, Z)U. (7.108)

Let us deﬁne a type (1, 1) tensor ﬁeld B by

BX ≡−X[σ ]U +∇

U +

U[σ ]X. (7.109)

Since g(∇

U, Z) =∇

dσ, Z  (exercise 7.8(c)), (7.108) becomes

R(X, Y )Z = R(X, Y )Z −[g(Y, Z )BX − g(BX, Z)Y

+ g(BY, Z)X − g(X, Z)BY]. (7.110)

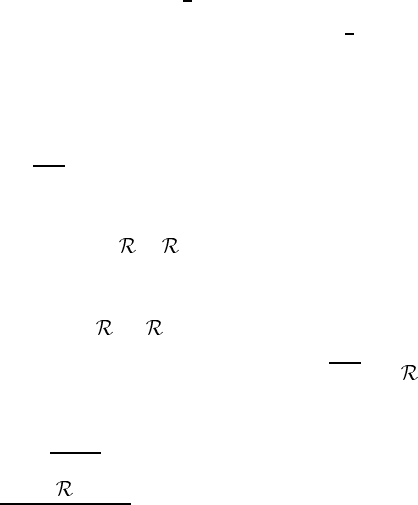
In components, this becomes

λµν

= R

λµν

− g

νλ

+ g

ξλ

− g

ξλ

+ g

µλ

(7.111)

where the components of the tensor B are

=−∂

σ U

+ (∇

U[σ ]δ

=−∂

σ g

κλ

∂

σ + g

κλ

(∂

∂

σ − 

µλ

∂

σ)+

λξ

∂

σ∂

σδ

(7.112)

Note that B

µν

≡ g

νλ

= B

νµ

By contracting the indices in (7.111), we obtain

Ric

µν

= Ric

µν

− g

µν

− (m − 2)B

νµ

(7.113)

2σ

= − 2(m − 1)B

(7.114a)

where m = dim M. Equation (7.114a) is also written as

¯g

µν

=[ − 2(m − 1)B

µν

. (7.114b)

If we eliminate g

µν

and B

µν

λµν

in favour of Ric and

and separate

barred and unbarred terms, we ﬁnd a combination which is independent of σ ,

κλµν

= R

κλµν

m − 2

(Ric

κµ

λν

− Ric

λµ

κν

+ Ric

λν

κµ

− Ric

κν

λµ

)

(m − 2)(m − 1)

κµ

λν

− g

κν

λµ

) (7.115)

where m ≥ 4 (see problem 7.2 for m = 3). The tensor C is called the Weyl

tensor. The reader should verify that C

κλµν

If every point p of a (pseudo-)Riemannian manifold (M, g) has a chart

(U,ϕ) containing p such that g

µν

= e

2σ

µν

,then(M, g) is said to be

conformally ﬂat. Since the Weyl tensor vanishes for a ﬂat metric, it also vanishes

for a conformally ﬂat metric. If dim M ≥ 4, then C = 0 is the necessary and

sufﬁcient condition for conformal ﬂatness (Weyl–Schouten). If dim M = 3, the

Weyl tensor vanishes identically; see problem 7.2. If dim M = 2, M is always

conformally ﬂat; see the next example.

Example 7.9. Any two-dimensional Riemannian manifold (M, g) is conformally

ﬂat. Let (x , y) be the original local coordinates with which the metric takes the

form

= g

+ 2g

dx dy + g

. (7.116)

Let g ≡ g

− g

and write (7.116) as



√

dx +

+ i

√



√

dx +

− i

√



According to the theory of differential equations, there exists an integrating factor

λ(x, y) = λ

(x , y) + iλ

(x , y) such that



√

dx +

+ i

√



= du + idv (7.117a)



√

dx +

− i

√



= du − idv. (7.117b)

Then ds

= (du

+ dv

)/|λ|

and by setting |λ|

−2

= e

2σ

, we have the desired

coordinate system. The coordinates (u,v)are called the isothermal coordinates.

[Remark:Ifthecurveu = a constant is regarded as an isothermal curve, v = a

constant corresponds to the line of heat ﬂow.]

For example, let ds

= dθ

+sin

θ dφ

be the standard metric of S

. Noting

that

dθ

log



tan



sin θ

we ﬁnd that f : (θ, φ) → (u,v) deﬁned by u = log |tan

θ| and v = φ yields a

conformally ﬂat metric. In fact,

= sin



dθ

sin

+ dφ



= sin

θ(du

+ dv

If (M, g) is a Lorentz manifold, we have integrating factors λ(x , y) and

µ(x, y) such that



√

dx +

√

−g

√



= du + dv (7.118a)



√

dx +

−

√

−g

√



= du − dv. (7.118b)

In terms of the coordinates (u,v) the metric takes the form ds

= λ

−1

(du

−

). The product λµ is either positive deﬁnite or negative deﬁnite and we may

set 1/|λµ|=e

2σ

to obtain the form

=±e

2σ

(du

− dv

). (7.119)

Exercise 7.16. Let (M, g) be a two-dimensional Lorentz manifold with g =

−dt ⊗ dt + t

dx ⊗ dx (the Milne universe). Use the transformation |t| → e

show that g is conformally ﬂat. In fact, it is further simpliﬁed by (η, x ) → (u =

sinh x,v = e

cosh x). What is the resulting metric?

7.7 Killing vector ﬁelds and conformal Killing vector ﬁelds

7.7.1 Killing vector ﬁelds

Let (M, g) be a Riemannian manifold and X ∈

(M). If a displacement ε X, ε

being inﬁnitesimal, generates an isometry, the vector ﬁeld X is called a Killing

vector ﬁeld. The coordinates x

of a point p ∈ M change to x

+ε X

( p) under

this displacement, see (5.42). If f : x

→ x

+ εX

is an isometry, it satisﬁes

(7.96b),

∂(x

+ ε X

)

∂x

∂(x

+ ε X

)

∂x

κλ

(x + εX) = g

µν

(x ).

After a simple calculation, we ﬁnd that g

µν

and X

satisfy the Killing equation

∂

µν

+ ∂

κν

+ ∂

µλ

= 0. (7.120a)

From the deﬁnition of the Lie derivative, this is written in a compact form as

(

µν

= 0. (7.120b)

Let φ

: M → M be a one-parameter group of transformations which generates

the Killing vector ﬁeld X . Equation (7.120b) then shows that the local geometry

does not change as we move along φ

. In this sense, the Killing vector ﬁelds

represent the direction of the symmetry of a manifold.

A set of Killing vector ﬁelds are deﬁned to be dependent if one of them

is expressed as a linear combination of others with constant coefﬁcients. Thus,

there may be more Killing vector ﬁelds than the dimension of the manifold. [The

number of independent symmetries has no direct connection with dim M.The

maximum number, however, has; see example 7.10.]

Exercise 7.17. Let ∇ be the Levi-Civita connection. Show that the Killing

equation is written as

(∇

+ (∇

= ∂

+ ∂

− 2

µν

= 0. (7.121)

Exercise 7.18. Find three Killing vector ﬁelds of (

,δ). Show that two of

them correspond to translations while the third corresponds to a rotation; cf next

example.

Example 7.10. Let us work out the Killing vector ﬁelds of the Minkowski

spacetime (

,η), for which all the Levi-Civita connection coefﬁcients vanish.

The Killing equation becomes

∂

+ ∂

= 0. (7.122)

It is easy to see that X

is, at most, of the ﬁrst order in x . The constant solutions

(i)

= δ

(0 ≤ i ≤ 3) (7.123a)

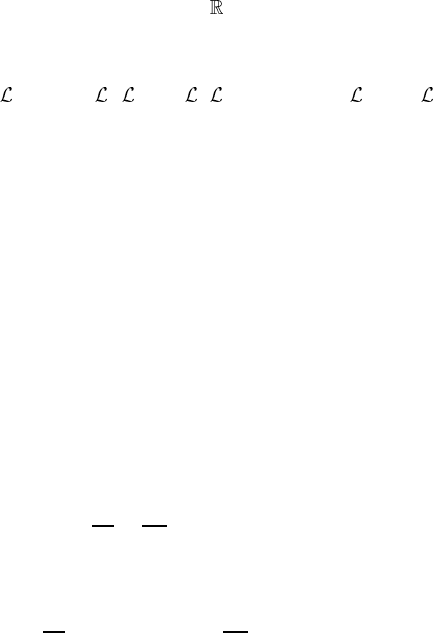
correspond to spacetime translations. Next, let X

= a

µν

, a

µν

being constant.

Equation (7.122) implies that a

µν

is anti-symmetric with respect to µ ↔ ν.Since



= 6, there are six independent solutions of this form, three of which

( j)0

= 0 X

( j)m

= ε

jmn

(1 ≤ j, m, n ≤ 3) (7.123b)

correspond to spatial rotations about the x

-axis, while the others

(k)0

= x

(k)m

=−δ

(1 ≤ k, m ≤ 3) (7.123c)

correspond to Lorentz boosts along the x

-axis.

In m-dimensional Minkowski spacetime (m ≥ 2),therearem(m + 1)/2

Killing vector ﬁelds, m of which generate translations, (m − 1), boosts and

(m − 1)(m − 2)/2, space rotations. Those spaces (or spacetimes) which admit

m(m + 1)/2 Killing vector ﬁelds are called maximally symmetric spaces.

Let X and Y be two Killing vector ﬁelds. We easily verify that

(i) a linear combination aX + bY (a, b ∈

) is a Killing vector ﬁeld; and

(ii) the Lie bracket [X, Y ] is a Killing vector ﬁeld.

(i) is obvious from the linearity of the covariant derivative. To prove (ii), we use

(5.58). We have

[X,Y ]

g =

X Y

g −

Y X

g = 0, since

g =

g = 0.

Thus, all the Killing vector ﬁelds form a Lie algebra of the symmetric operations

on the manifold M; see the next example.

Example 7.11. Let g = dθ ⊗ dθ + sin

θ dφ ⊗ dφ be the standard metric of S

The Killing equations (7.121) are:

∂

+ ∂

= 0 (7.124a)

∂

+ ∂

+ 2sinθ cos θ X

= 0 (7.124b)

∂

+ ∂

− 2cotθ X

= 0. (7.124c)

It follows from (7.124a) that X

is independent of θ : X

(θ, φ) = f (φ).

Substituting this into (7.124b), we have

=−F(φ) sin θ cos θ + g(θ) (7.125)

where F(φ) =



f (φ) dφ. Substitution of (7.125) into (7.124c) yields

−F(φ)(cos

θ − sin

θ) +

dθ

d f

dφ

+ 2cotθ(F(φ) sin θ cos θ − g(θ)) = 0.

This equation may be separated into

dθ

− 2cotθg(θ ) =−

d f

dφ

− F(φ).

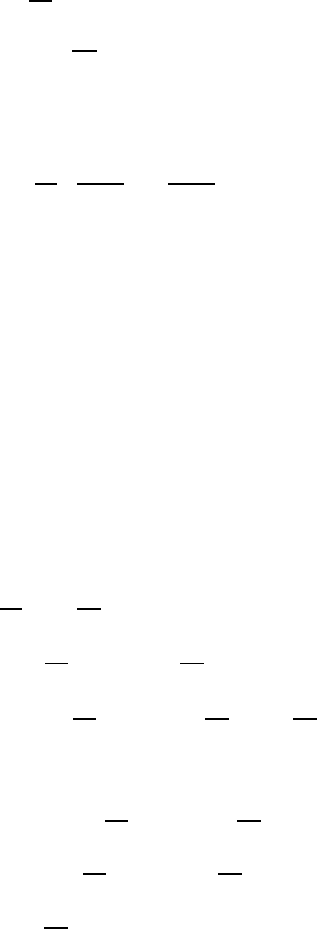
Since both sides must be separately constant (≡C),wehave

dθ

− 2cotθg(θ ) = C (7.126a)

d f

dφ

+ F(φ) =−C. (7.126b)

Equation (7.126a) is solved if we multiply both sides by exp(−



dθ 2cotθ) =

sin

−2

θ to make the LHS a total derivative,

dθ



g(θ )

sin



sin

The solution is easily found to be

g(θ ) = (C

− C cot θ)sin

θ.

Differentiating (7.126b) again, we ﬁnd that f is harmonic,

(φ) = f (φ) = A sin φ + B cos φ

F(φ) =−A cos φ + B sin φ − C.

Substituting these results into (7.125), we have

(θ, φ) =−(−A cos φ + B sin φ − C) sin θ cos θ + (C

− C cot θ)sin

= (A cos φ − B sin φ) sin θ cos θ + C

sin

θ.

A general Killing vector is given by

X = X

∂

∂θ

+ X

∂

∂φ

= A



sin φ

∂

∂θ

+ cos φ cot θ

∂

∂φ



+ B



cos φ

∂

∂θ

− sin φ cot θ

∂

∂φ



+ C

∂

∂φ

. (7.127)

The basis vectors

=−cos φ

∂

∂θ

+ cot θ sin φ

∂

∂φ

(7.128a)

= sin φ

∂

∂θ

+ cot θ cos φ

∂

∂φ

(7.128b)

∂

∂φ

(7.128c)

generate rotations round the x, y and z axes respectively.