Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

loop. Since M is simply connected, there exists a homotopy F(s, t) such that

F(s, 0) = α(s) and F(s, 1) = c

(s). We assume F : I × I → M is smooth.

Deﬁne the integral of a one-form ω over α(I ) by



α(I )

ω =



∗

ω (6.57)

wherewehavetakentheintegraldomainintheRHStobeS

since I =[0, 1] in

the LHS is compactiﬁed to S

. From lemma 6.1, we have, for a closed one-form

ω,

∗

ω − c

∗

ω = dg (6.58)

where g =−PF

∗

ω. The pullback c

ω vanishes since c

is a constant map. Then

(6.57) vanishes since ∂ S

is empty,



∗

ω =



dg =



∂ S

g = 0. (6.59)

Let β and γ be two paths connecting p

and p. According to (6.59), integrals

of ω along β and along γ are identical,



β(I )

ω =



γ(I )

ω.

This shows that (6.56) is indeed well deﬁned, hence ω is exact.

Example 6.6. The n-sphere S

(n ≥ 2) is simply connected, hence

) = 0 n ≥ 2. (6.60)

From the Poincar´e duality, we ﬁnd

)

∼

) = . (6.61)

It can be shown that

) = 01≤ r ≤ n − 1. (6.62)

) is generated by the volume element . Since there are no (n + 1)-forms

on S

,everyn-form is closed.  cannot be exact since if  = dψ, we would

have



 =



dψ =



∂ S

ψ = 0.

The Euler characteristic is

χ(S

) = 1 +(−1)



0 n is odd,

2 n is even.

(6.63)

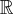
Example 6.7. Take S

embedded in

and deﬁne

 = sin θ dθ ∧dφ (6.64)

where (θ, φ) is the usual polar coordinate. Verify that  is closed. We may

formally write  as

 =−d(cos θ) ∧dφ =−d(cos θ dφ).

Note, however, that  is not exact.

RIEMANNIAN GEOMETRY

A manifold is a topological space which locally looks like

. Calculus on a

manifold is assured by the existence of smooth coordinate systems. A manifold

may carry a further structure if it is endowed with a metric tensor, which is

a natural generalization of the inner product between two vectors in

to an

arbitrary manifold. With this new structure, we deﬁne an inner product between

two vectors in a tangent space T

M. We may also compare a vector at a point

p ∈ M with another vector at a different point p



∈ M with the help of the

‘connection’.

There are many books about Riemannian geometry. Those which are

accessible to physicists are Choquet-Bruhat et al (1982), Dodson and Poston

(1977) and Hicks (1965). Lightman et al (1975) and chapter 3 of Wald (1984)

are also recommended.

7.1 Riemannian manifolds and pseudo-Riemannian manifolds

7.1.1 Metric tensors

In elementary geometry, the inner product between two vectors U and V is

deﬁned by U · V =



i=1

where U

and V

are the components of the

vectors in

. On a manifold, an inner product is deﬁned at each tangent space

Deﬁnition 7.1. Let M be a differentiable manifold. A Riemannian metric g on

M is a type (0, 2) tensor ﬁeld on M which satisﬁes the following axioms at each

point p ∈ M:

(i) g

(U, V ) = g

(V , U),

(ii) g

(U, U ) ≥ 0, where the equality holds only when U = 0.

Here U, V ∈ T

M and g

= g|

. In short, g

is a symmetric positive-deﬁnite

bilinear form.

A tensor ﬁeld g of type (0, 2) is a pseudo-Riemannian metric if it satisﬁes

(i) and

(ii



)ifg

(U, V ) = 0foranyU ∈ T

M,thenV = 0.

In chapter 5, we have deﬁned the inner product between a vector V ∈ T

and a dual vector ω ∈ T

∗

M as a map  , :T

∗

M × T

M → .Ifthere

exists a metric g, we deﬁne an inner product between two vectors U, V ∈ T

by g

(U, V ).Sinceg

is a map T

M ⊗ T

M → we may deﬁne a linear

map g

(U,): T

M → by V → g

(U, V ).Theng

(U,)is identiﬁed

with a one-form ω

∈ T

∗

M. Similarly, ω ∈ T

∗

M induces V

∈ T

M by

ω,U =g(V

, U ). Thus, the metric g

gives rise to an isomorphism between

M and T

∗

Let (U,ϕ)be a chart in M and {x

} the coordinates. Since g ∈

(M),itis

expanded in terms of dx

⊗ dx

= g

µν

( p)dx

⊗ dx

. (7.1a)

It is easily checked that

µν

( p) = g



∂

∂x

∂

∂x



= g

νµ

( p)(p ∈ M). (7.1b)

We usually omit p in g

µν

unless it may cause confusion. It is common to

regard (g

µν

) as a matrix whose (µ, ν)th entry is g

µν

.Since(g

µν

) has the

maximal rank, it has an inverse denoted by (g

µν

) according to the tradition:

µν

νλ

= g

λν

νµ

= δ

. The determinant det(g

µν

) is denoted by g. Clearly

det(g

µν

) = g

−1

. The isomorphism between T

M and T

∗

M is now expressed as

= g

µν

, U

= g

µν

. (7.2)

From (7.1a) and (7.1b) we recover the ‘old-fashioned’ deﬁnition of the

metric as an inﬁnitesimal distance squared. Take an inﬁnitesimal displacement

∂/∂x

∈ T

M and plug it into g to ﬁnd

= g



∂

∂x

, dx

∂

∂x



= dx



∂

∂x

∂

∂x



= g

µν

. (7.3)

We also call the quantity ds

= g

µν

a metric, although in a strict sense

themetricisatensor g = g

µν

⊗ dx

Since (g

µν

) is a symmetric matrix, the eigenvalues are real. If g

is Riemannian, all the eigenvalues are strictly positive and if g is pseudo-

Riemannian, some of them may be negative. If there are i positive and j negative

eigenvalues, the pair (i, j ) is called the index of the metric. If j = 1, the metric

is called a Lorentz metric. Once a metric is diagonalized by an appropriate

orthogonal matrix, it is easy to reduce all the diagonal elements to ±1 by a suitable

scaling of the basis vectors with positive numbers. If we start with a Riemannian

metric we end up with the Euclidean metric δ = diag(1,...,1) and if we start

with a Lorentz metric, the Minkowski metric η = diag(−1, 1,...,1).

If (M, g) is Lorentzian, the elements of T

M are divided into three classes

as follows,

(i) g(U, U)>0 −→ U is spacelike,

(ii) g(U, U ) = 0 −→ U is lightlike (or null), (7.4)

(iii) g(U, U )<0 −→ U is timelike.

Exercise 7.1. Diagonalize the metric

µν

) =







0100

1000

0010

0001







to show that it reduces to the Minkowski metric. The frame on which the

metric takes this form is known as the light cone frame.Let{e

, e

}

be the basis of the Minkowski frame in which the metric is g

µν

= η

µν

.Show

that {e

, e

−

, e

} are the basis vectors in the light cone frame, where e

≡

± e

√

2. Let V = (V

, V

−

, V

) be components of a vector V .Find

the components of the corresponding one-form.

If a smooth manifold M admits a Riemannian metric g, the pair (M, g) is

called a Riemannian manifold.Ifg is a pseudo-Riemannian metric, (M, g)

is called a pseudo-Riemannian manifold.Ifg is Lorentzian, (M, g) is called

a Lorentz manifold. Lorentz manifolds are of special interest in the theory

of relativity. For example, an m-dimensional Euclidean space (

,δ) is a

Riemannian manifold and an m-dimensional Minkowski space (

,η) is a

Lorentz manifold.

7.1.2 Induced metric

Let M be an m-dimensional submanifold of an n-dimensional Riemanian

manifold N with the metric g

.If f : M → N is the embedding which induces

the submanifold structure of M (see section 5.2), the pullback map f

∗

induces

the natural metric g

= f

∗

on M. The components of g

are given by

Mµν

(x ) = g

Nαβ

( f (x))

∂ f

∂x

∂ f

∂x

(7.5)

where f

denote the coordinates of f (x ). For example, consider the metric of the

unit sphere embedded in (

,δ).Let(θ, φ) be the polar coordinates of S

and

deﬁne f by the usual inclusion

f : (θ, φ) → (sin θ cos φ,sin θ sin φ,cos θ)

from which we obtain the induced metric

µν

⊗ dx

= δ

αβ

∂ f

∂x

∂ f

∂x

⊗ dx

= dθ ⊗ dθ + sin

θ dφ ⊗ dφ. (7.6)

Exercise 7.2. Let f : T

→

be an embedding of the torus into (

,δ)deﬁned

f : (θ, φ) → ((R +r cos θ)cos φ,(R + r cos θ)sin φ,r sin θ)

where R > r. Show that the induced metric on T

g = r

dθ ⊗ dθ + (R + r cos θ)

dφ ⊗ dφ. (7.7)

When a manifold N is pseudo-Riemannian, its submanifold f : M → N

need not have a metric f

∗

. The tensor f

∗

is a metric only when it has a

ﬁxed index on M.

7.2 Parallel transport, connection and covariant derivative

A vector X is a directional derivative acting on f ∈

(M) as X : f → X[ f ].

However, there is no directional derivative acting on a tensor ﬁeld of type ( p, q),

which arises naturally from the differentiable structure of M. [Note that the Lie

derivative

X =[V , X ] is not a directional derivative since it depends on the

derivative of V .] What we need is an extra structure called the connection,which

speciﬁes how tensors are transported along a curve.

7.2.1 Heuristic introduction

We ﬁrst give a heuristic approach to parallel transport and covariant derivatives.

As we have noted several times, two vectors deﬁned at different points cannot be

compared naively with each other. Let us see how the derivative of a vector ﬁeld

in a Euclidean space

is deﬁned. The derivative of a vector ﬁeld V = V

with respect to x

has the µth component

∂V

∂x

= lim

x→0

(...,x

+ x

,...)− V

(...,x

,...)

x

The ﬁrst term in the numerator of the LHS is deﬁned at x + x = (x

,...,x

x

,...,x

), while the second term is deﬁned at x = (x

). To subtract V

(x )

from V

(x + x), we have to transport V

(x ) to x + x without change and

compute the difference. This transport of a vector is called a parallel transport.

We have implicitly assumed that V

parallel transported to x +x has the same

component V

(x ). However, there is no natural way to parallel transport a vector

in a manifold and we have to specify how it is parallel transported from one point

to the other. Let

(

V |

x+x

denote a vector V |

parallel transported to x + x .We

demand that the components satisfy

(

(x + x ) − V

(x ) ∝ x (7.8a)

+ W

)(x + x ) =

(

(x + x) +

(

(x + x ). (7.8b)

These conditions are satisﬁed if we take

(

(x + x ) = V

(x ) − V

(x )

νλ

(x )x

. (7.9)

The covariant derivative of V with respect to x

is deﬁned by

lim

x

→0

(x + x ) −

(

(x + x )

x

∂

∂x



∂V

∂x

+ V



νλ



∂

∂x

. (7.10)

This quantity is a vector at x + x since it is a difference of two vectors V |

x+x

and

(

V |

x+x

deﬁned at the same point x + x . There are many distinct rules

of parallel transport possible, one for each choice of . If the manifold is

endowed with a metric, there exists a preferred choice of , called the Levi-Civita

connection, see example 7.1 and section 7.4.

Example 7.1. Let us work out a simple example: two-dimensional Euclidean

space (

,δ). We deﬁne parallel transportation according to the usual sense

in elementary geometry. In the Cartesian coordinate system (x, y), all the

components of  vanish since

(

(x + x , y + y) = V

(x , y) for any x

and y. Next we take the polar coordinates (r,φ).If(r,φ) → (r cos φ,r sin φ)

is regarded as an embedding, we ﬁnd the induced metric,

g = dr ⊗ dr + r

dφ ⊗ dφ. (7.11)

Let V = V

∂/∂r +V

∂/∂φ be a vector deﬁned at (r,φ). If we parallel transport

this vector to (r + r,φ), we have a new vector

(

V =

(

∂/∂r

(r+r,φ)

(

∂/∂φ

(r+r,φ)

(ﬁgure 7.1(a)). Note that V

= V cos θ and V

= V (sin θ/r ),

where V =

√

g(V, V) and θ is the angle between V and ∂/∂r.Thenwehave

(

= V

and

(

r + r

 V

−

r

By comparing these components with (7.9), we easily ﬁnd that



= 0 

rφ

= 0 

rφ

. (7.12a)

Similarly, if V is parallel transported to (r,φ+ φ), it becomes

(

V =

(

∂

∂r



(r,φ+φ)

(

∂

∂φ



(r,φ+φ)

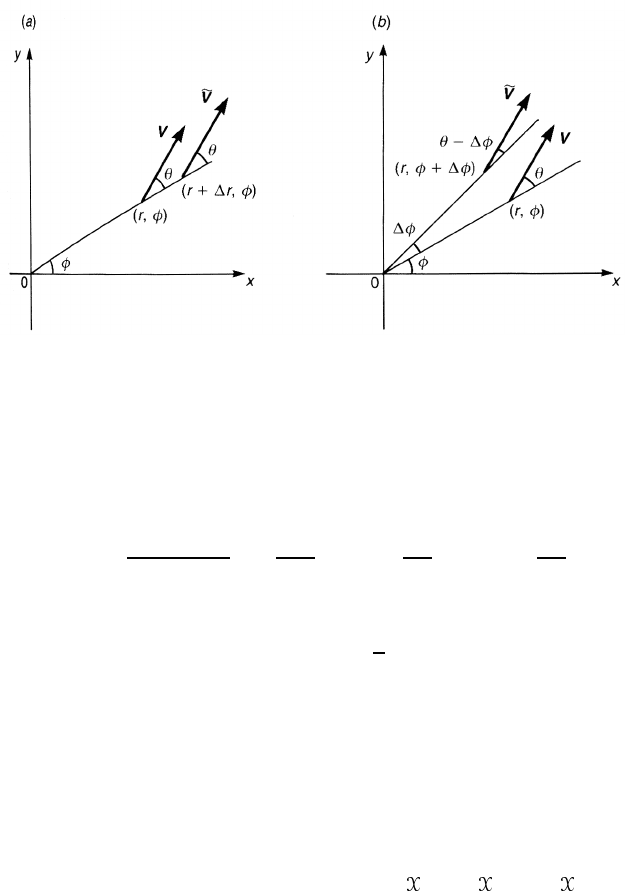
Figure 7.1.

(

V is a vector V parallel transported to (a) (r + r,φ) and (b) (r,φ+ φ).

where

(

= V cos(θ − φ)  V cos θ + V sin θφ = V

+ V

rφ

and

(

= V

sin(θ − φ)

 V

sin θ

− V cos θ

φ

= V

− V

φ

(ﬁgure 7.1(b)). Then we ﬁnd



φr

= 0 

φφ

=−r 

φr



φφ

= 0. (7.12b)

Note that the  satisfy the symmetry 

µν

= 

νµ

. It is also implicitly assumed

that the norm of a vector is invariant under parallel transport. A rule of parallel

transport which satisﬁes these two conditions is called a Levi-Civita connection,

see section 7.4. Our intuitive approach leads us to the formal deﬁnition of the

afﬁne connection.

7.2.2 Afﬁne connections

Deﬁnition 7.2. An afﬁne connection ∇ is a map ∇:

(M) × (M) → (M),or

(X, Y ) →∇

Y which satisﬁes the following conditions:

∇

(Y + Z ) =∇

Y +∇

Z (7.13a)

∇

(X+Y )

Z =∇

Z +∇

Z (7.13b)

∇

( fX)

Y = f ∇

Y (7.13c)

∇

( fY) = X[ f ]Y + f ∇

Y (7.13d)

where f ∈ (M) and X, Y, Z ∈ (M).

Takeachart(U,ϕ) with the coordinate x = ϕ(p) on M, and deﬁne m

functions 

νµ

called the connection coefﬁcients by

∇

≡∇

= e



νµ

(7.14)

where {e

}={∂/∂x

} is the coordinate basis in T

M. The connection

coefﬁcients specify how the basis vectors change from point to point. Once the

action of ∇ on the basis vectors is deﬁned, we can calculate the action of ∇ on

any vectors. Let V = V

and W = W

be elements of T

(M).Then

∇

W = V

∇

) = V

+ W

∇

)

= V



∂W

∂x

+ W



µν



. (7.15)

Note that this deﬁnition of the connection coefﬁcient is in agreement with the

previous heuristic result (7.10). By deﬁnition, ∇ maps two vectors V and W to a

new vector given by the RHS of (7.15), whose λth component is V

∇

where

∇

≡

∂W

∂x

+ 

µν

. (7.16)

Note that ∇

is the λth component of a vector ∇

W =∇

and should

not be confused with the covariant derivative of a component W

. ∇

W is

independent of the derivative of V , unlike the Lie derivative

W =[V, W ].

In this sense, the covariant derivative is a proper generalization of the directional

derivative of functions to tensors.

7.2.3 Parallel transport and geodesics

Given a curve in a manifold M, we may deﬁne the parallel transport of a vector

along the curve. Let c : (a, b) → M be a curve in M. For simplicity, we assume

the image is covered by a single chart (U,ϕ)whose coordinate is x = ϕ(p).Let

X be a vector ﬁeld deﬁned (at least) along c(t),

c(t )

= X

(c(t))e

c(t )

(7.17)

where e

= ∂/∂x

.IfX satisﬁes the condition

∇

X = 0foranyt ∈ (a, b) (7.18a)

X is said to be parallel transported along c(t) where V = d/dt=

(dx

(c(t))/dt)e

c(t )

is the tangent vector to c(t). The condition (7.18a) is

written in terms of the components as

+ 

νλ

(c(t))

= 0. (7.18b)

If the tangent vector V (t) itself is parallel transported along c(t), namely if

∇

V = 0 (7.19a)

the curve c(t) is called a geodesic. Geodesics are, in a sense, the straightest

possible curves in a Riemannian manifold. In components, the geodesic

equation (7.19a) becomes

+ 

νλ

= 0 (7.19b)

where {x

} are the coordinates of c(t). We might say that (7.19a) is too strong to

be the condition for the straightest possible curve, and instead require a weaker

condition

∇

V = fV (7.20)

where f ∈

(M). ‘Change of V is parallel to V ’ is also a feature of a straight

line. However, under the reparametrization t → t



, the component of the tangent

vector changes as

→



and (7.20) reduces to (7.19a) if t



satisﬁes



= f



Thus, it is always possible to reparametrize the curve so that the geodesic equation

takes the form (7.19a).

Exercise 7.3. Show that (7.19b) is left invariant under the afﬁne reparametrization

t → at + b (a, b ∈

7.2.4 The covariant derivative of tensor ﬁelds

Since ∇

has the meaning of a derivative, it is natural to deﬁne the covariant

derivative of f ∈

(M) by the ordinary directional derivative:

∇

f = X [ f ]. (7.21)

Then (7.13d) looks exactly like the Leibnitz rule,

∇

( fY) = (∇

f )Y + f ∇

Y.(7.13d



)

We require that this be true for any product of tensors,

∇

⊗ T

) = (∇

) ⊗ T

+ T

⊗ (∇

) (7.22)