Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.

Let A be an element of G
k,n
( ),thenA is a k-dimensional plane in
n
. Define an
n×n matrix P
A
which projects a vector v ∈
n
to the plane A. Let us introduce an
orthonormal basis {e
1
,...,e
n
} in
n
and another orthonormal basis {f
1
,..., f
k
}
in the plane A, where the orthonormality is defined with respect to the Euclidean
metric in
n
.Intermsof{e
i
}, f
a
is expanded as f
a
=
i
f
ai
e
i
and the projected
vector is
P
A
v = (v f
1
) f
1
+···+(v f
k
) f
k
=
i, j
(v
i
f
1i
f
1 j
+···+v
i
f
ki
f
kj
)e
j
=
i,a, j
v
i
f
ai
f
aj
e
j
.
Thus, P
A
is represented by a matrix
(P
A
)
ij
=
f
ai
f
aj
. (5.155)
Note that P
2
A
= P
A
, P
t
A
= P
A
and tr P
A
= k. [The last relation holds since it is
always possible to choose a coordinate system such that
P
A
= diag(1, 1,...,1
,
-. /
k
, 0,...,0
,
-. /
n−k
).
This guarantees that A is, indeed, a k-dimensional plane.] Conversely any matrix
P that satisfies these three conditions determines a unique k-dimensional plane in
n
, that is a unique element of G
k,n
( ).
We now show that O(n) acts on G
k,n
( ) transitively. Take A ∈ G
k,n
( ) and
g ∈ O(n) and construct P
B
≡ gP
A
g
−1
. The matrix P
B
determines an element
B ∈ G
k,n
( ) since P
2
B
= P
B
, P
t
B
= P
B
and tr P
B
= k. Let us denote this
action by B = σ(g, A). Clearly this action is transitive since given a standard
k-dimensional basis of A, { f
1
,..., f
k
} for example, any k-dimensional basis
{
(
f
1
,...,
(
f
k
} can be reached by an action of O(n) on this basis.
Let us take a special plane C
0
which is spanned by the standard basis
{ f
1
,..., f
k
}. Then an element of the isotropy group H (C
0
) is of the form
kn− k
M =
g
1
0
0 g
2
k
n − k
(5.156)
where g
1
∈ O(k).SinceM ∈ O(n),an(n − k) × (n − k) matrix g
2
must be an
element of O(n −k). Thus, the isotropy group is isomorphic to O(k) ×O(n −k).
Finally we verified that
G
k,n
( )
∼
=
O(n)/[O(k) × O(n − k)]. (5.157)
The dimension of G
k,n
( ) is obtained from the general formula as
dim G
k,n
( ) = dim O(n) − dim[O(k) × O(n − k)]
=
1
2
n(n − 1) −[
1
2
k(k − 1) +
1
2
(n − k)(n − k − 1)]
= k(n − k) (5.158)

in agreement with the result of example 5.5. Equation (5.157) also shows that the
Grassmann manifold is compact.
5.7.3 Induced vector fields
Let G be a Lie group which acts on M as (g, x ) → gx. A left-invariant vector
field X
V
generated by V ∈ T
e
G naturally induces a vector field in M.Definea
flow in M by
σ(t, x ) = exp(tV)x , (5.159)
σ(t, x ) is a one-parameter group of transformations, and define a vector field
called the induced vector field denoted by V
,
V
|
x
=
d
dt
exp(tV)x
t=0
. (5.160)
Thus, we have obtained a map : T
e
G → (M) defined by V → V
.
Exercise 5.27. The Lie group SO(2) acts on M =
2
in the usual way. Let
V =
0 −1
10
be an element of
(2).
(a) Show that
exp(tV) =
cos t −sin t
sin t cos t
and find the induced flow through
x =
x
y
∈
2
.
(b) Show that V
|
x
=−y∂/∂x + x ∂/∂y.
Example 5.19. Let us take G = SO(3) and M =
3
. The basis vectors of T
e
G
are generated by rotations about the x , y and z axes. We denote them by X
x
, X
y
and X
z
, respectively (see exercise 5.22),
X
x
=
00 0
00−1
01 0
, X
y
=
001
000
−100
, X
z
=
0 −10
100
000
.
Repeating a similar analysis to the previous one, we obtain the corresponding
induced vectors,
X
x
=−z
∂
∂y
+ y
∂
∂z
, X
y
=−x
∂
∂z
+ z
∂
∂x
, X
z
=−y
∂
∂x
+ x
∂
∂y
.
5.7.4 The adjoint representation
A Lie group G acts on G itself in a special way.
Definition 5.17. Take any a ∈ G and define a homomorphism ad
a
: G → G by
the conjugation,
ad
a
: g → aga
−1
. (5.161)
This homomorphism is called the adjoint representation of G.
Exercise 5.28. Show that ad
a
is a homomorphism. Define a map σ : G ×G → G
by σ(a, g) ≡ ad
a
g. Show that σ(a, g) is an action of G on itself.
Noting that ad
a
e = e, we restrict the induced map ad
a∗
: T
g
G → T
ad
a
g
G to
g = e,
Ad
a
: T
e
G → T
e
G (5.162)
where Ad
a
≡ ad
a∗
|
T
e
G
. If we identify T
e
G with the Lie algebra ,wehave
obtained a map Ad : G ×
→ called the adjoint map of G.Since
ad
a∗
ad
b∗
= ad
ab∗
, it follows that Ad
a
Ad
b
= Ad
ab
. Similarly, Ad
a
−1
= Ad
−1
a
follows from ad
a
−1
∗
ad
a∗
|
T
e
G
= id
T
e
G
.
If G is a matrix group, the adjoint representation becomes a simple matrix
operation. Let g ∈ G and X
V
∈ ,andletσ
V
(t) = exp(tV) be a one-
parameter subgroup generated by V ∈ T
e
G.Thenad
g
acting on σ
V
(t) yields
g exp(tV)g
−1
= exp(tgVg
−1
).AsforAd
g
we have Ad
g
: V → gVg
−1
since
Ad
g
V =
d
dt
[ad
g
exp(tV)]
t=0
=
d
dt
exp(tgVg
−1
)
t=0
= gVg
−1
. (5.163)
Problems
5.1 The Stiefel manifold V (m, r ) is the set of orthonormal vectors {e
i
} (1 ≤ i ≤
r) in
m
(r ≤ m). We may express an element A of V (m, r) by an m ×r matrix
(e
1
,...,e
r
). Show that SO(m) acts transitively on V (m, r).Let
A
0
≡
10... 0
01... 0
... ... ... ...
00... 1
00... 0
00... 0
be an element of V (m, r). Show that the isotropy group of A
0
is SO(m−r ).Verify
that V (m, r) = SO(m)/SO(m −r) and dim V (m, r ) =[r(r −1)]/2 +r(m −r).
[Remark: The Stiefel manifold is, in a sense, a generalization of a sphere. Observe
that V (m, 1) = S
m−1
.]

5.2 Let M be the Minkowski four-spacetime. Define the action of a linear operator
∗:
r
(M) →
4−r
(M) by
r = 0 :∗1 =−dx
0
∧ dx
1
∧ dx
2
∧ dx
3
;
r = 1 :∗dx
i
=−dx
j
∧ dx
k
∧ dx
0
∗ dx
0
=−dx
1
∧ dx
2
∧ dx
3
;
r = 2 :∗dx
i
∧ dx
j
= dx
k
∧ dx
0
∗ dx
i
∧ dx
0
=−dx
j
∧ dx
k
;
r = 3 :∗dx
1
∧ dx
2
∧ dx
3
=−dx
0
∗ dx
i
∧ dx
j
∧ dx
0
=−dx
k
;
r = 4 :∗dx
0
∧ dx
1
∧ dx
2
∧ dx
3
= 1;
where (i, j, k) is an even permutation of (1, 2, 3). The vector potential A and
the electromagnetic tensor F are defined as in example 5.11. J = J
µ
dx
µ
=
ρdx
0
+ j
k
dx
k
is the current one-form.
(a) Write down the equation d ∗ F =∗J and verify that it reduces to two of the
Maxwell equations ∇·E = ρ and ∇×B − ∂ E/∂t = j.
(b) Show that the identity 0 = d(d ∗ F) = d ∗ J reduces to the charge
conservation equation
∂
µ
J
µ
=
∂ρ
∂t
+∇·j = 0.
(c) Show that the Lorentz condition ∂
µ
A
µ
= 0 is expressed as d ∗ A = 0.

6
DE RHAM COHOMOLOGY GROUPS
The homology groups of topological spaces have been defined in chapter 3. If
a topological space M is a manifold, we may define the dual of the homology
groups out of differential forms defined on M. The dual groups are called the
de Rham cohomology groups. Besides physicists’ familiarity with differential
forms, cohomology groups have several advantages over homology groups.
We follow closely Nash and Sen (1983) and Flanders (1963). Bott and Tu
(1982) contains more advanced topics.
6.1 Stokes’ theorem
One of the main tools in the study of de Rham cohomology groups is Stokes’
theorem with which most physicists are familiar from electromagnetism. Gauss’
theorem and Stokes’ theorem are treated in a unified manner here.
6.1.1 Preliminary consideration
Let us define an integration of an r-form over an r -simplex in a Euclidean space.
To do this, we need first to define the standard n-simplex ¯σ
r
= ( p
0
p
1
...p
r
) in
r
where
p
0
= (0, 0,...,0)
p
1
= (1, 0,...,0)
...
p
r
= (0, 0,...,1)
see figure 6.1. If {x
µ
} is a coordinate of
r
, ¯σ
r
is given by
¯σ
r
=
(x
1
,...,x
r
) ∈
r
x
µ
≥ 0,
r
µ=1
x
µ
≤ 1
. (6.1)
An r -form ω (the volume element) in
r
is written as
ω = a(x ) dx
1
∧ dx
2
∧ ...∧ dx
r
.
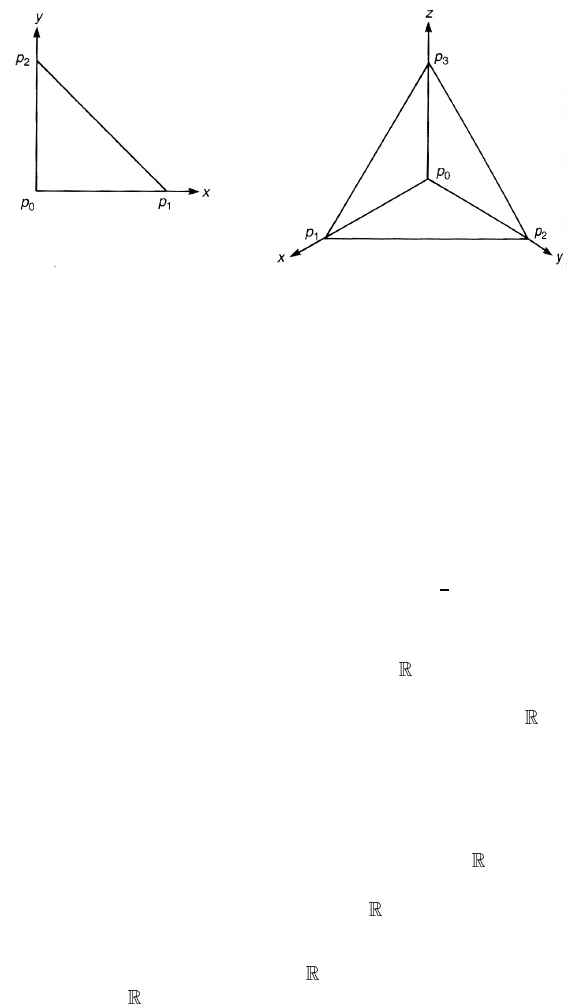
Figure 6.1. The standard 2-simplex ¯σ
2
= (p
0
p
1
p
2
) and the standard 3-simplex
¯σ
3
= ( p
0
p
1
p
2
p
3
).
We define the integration of ω over ¯σ
r
by
¯σ
r
ω ≡
¯σ
r
a(x ) dx
1
dx
2
...dx
r
(6.2)
where the RHS is the usual r-fold integration. For example, if r = 2and
ω = dx ∧ dy,wehave
¯σ
2
ω =
¯σ
2
dx dy =
1
0
dx
1−x
0
dy =
1
2
.
Next we define an r-chain, an r-cycle and an r -boundary in an m-
dimensional manifold M.Letσ
r
be an r -simplex in
r
and let f : σ
r
→ M
be a smooth map. [To avoid the subtlety associated with the differentiability of
f at the boundary of σ
r
, f may be defined over an open subset U of
r
,which
contains σ
r
.] Here we assume f is not required to have an inverse. For example,
im f may be a point in M. We denote the image of σ
r
in M by s
r
and call it a
(singular) r-simplex in M. These simplexes are called singular since they do not
provide a triangulation of M and, moreover, geometrical independence of points
makes no sense in a manifold (see section 3.2). If {s
r,i
} is the set of r -simplexes
in M, we define an r-chain in M by a formal sum of {s
r,i
} with -coefficients
c =
i
a
i
s
r,i
a
i
∈ . (6.3)
In the following, we are concerned with
-coefficients only and we omit the
explicit quotation of
.Ther-chains in M form the chain group C
r
(M). Under
f : σ
r
→ M, the boundary ∂σ
r
is also mapped to a subset of M. Clearly,
∂s
r
≡ f (∂σ
r
) is a set of (r − 1)-simplexes in M and is called the boundary of

s
r
. ∂s
r
corresponds to the geometrical boundary of s
r
with an induced orientation
defined in section 3.3. We have a map
∂ : C
r
(M) → C
r−1
(M). (6.4)
The result of section 3.3 tells us that ∂ is nilpotent; ∂
2
= 0.
Cycles and boundaries are defined in exactly the same way as in section 3.3
(note, however, that
is replaced by ). If c
r
is an r-cycle, ∂c
r
= 0 while if c
r
is an r-boundary, there exists an (r + 1)-chain c
r+1
such that c
r
= ∂c
r+1
.The
boundary group B
r
(M) is the set of r -boundaries and the cycle group Z
r
(M)
is the set of r -cycles. There are infinitely many singular simplexes which make
up C
r
(M), B
r
(M) and Z
r
(M). It follows from ∂
2
= 0thatZ
r
(M) ⊃ B
r
(M);cf
theorem 3.3. The singular homology group is defined by
H
r
(M) ≡ Z
r
(M)/B
r
(M). (6.5)
With mild topological assumptions, the singular homology group is isomorphic to
the corresponding simplicial homology group with
-coefficients and we employ
the same symbol to denote both of them.
Now we are ready to define an integration of an r -form ω over an r-chain in
M. We first define an integration of ω on an r -simplex s
r
of M by
s
r
ω =
¯σ
r
f
∗
ω (6.6)
where f :¯σ
r
→ M is a smooth map such that s
r
= f ( ¯σ
r
).Sincef
∗
ω is
an r-form in
r
, the RHS is the usual r -fold integral. For a general r -chain
c =
i
a
i
s
r,i
∈ C
r
(M),wedefine
c
ω =
i
a
i
s
r,i
ω. (6.7)
6.1.2 Stokes’ theorem
Theorem 6.1. (Stokes’ theorem)Letω ∈
r−1
(M) and c ∈ C
r
(M).Then
c
dω =
∂c
ω. (6.8)
Proof.Sincec is a linear combination of r -simplexes, it suffices to prove (6.8) for
an r -simplex s
r
in M.Let f :¯σ
r
→ M be a map such that f ( ¯σ
r
) = s
r
.Then
s
r
dω =
¯σ
r
f
∗
(dω) =
¯σ
r
d( f
∗
ω)
where (5.75) has been used. We also have
∂s
r
ω =
∂ ¯σ
r
f
∗
ω.

Note that f
∗
ω is an (r − 1)-form in
r
. Thus, to prove Stokes’ theorem
s
r
dω =
∂s
r
ω (6.9a)
it suffices to prove an alternative formula
¯σ
r
dψ =
∂ ¯σ
r
ψ (6.9b)
for an (r − 1)-form ψ in
r
. The most general form of ψ is
ψ =
a
µ
(x ) dx
1
∧ ...∧ dx
µ−1
∧ dx
µ+1
∧ ...∧ dx
r
.
Since an integration is distributive, it suffices to prove (6.9b) for ψ = a(x )dx
1
∧
...∧ dx
r−1
. We note that
dψ =
∂a
∂x
r
dx
r
∧ dx
1
∧ ...∧ dx
r−1
= (−1)
r−1
∂a
∂x
r
dx
1
∧ ...∧ dx
r−1
∧ dx
r
.
By direct computation, we find, from (6.2), that
¯σ
r
dψ = (−1)
r−1
¯σ
r
∂a
∂x
r
dx
1
...dx
r−1
dx
r
= (−1)
r−1
x
µ
≥0,
r−1
µ=1
x
µ
≤1
dx
1
...dx
r−1
1−
r−1
µ=1
x
µ
0
∂a
∂x
r
dx
r
= (−1)
r−1
dx
1
...dx
r−1
×
a
x
1
,...,x
r−1
, 1 −
r−1
µ=1
x
µ
− a
x
1
,...,x
r−1
, 0
.
For the boundary of ¯σ
r
,wehave
∂ ¯σ
r
= ( p
1
, p
2
,...,p
r
) − ( p
0
, p
2
,...,p
r
)
+···+(−1)
r
( p
0
, p
1
,...,p
r−1
).
Note that ψ = a(x)dx
1
∧ ... ∧ dx
r−1
vanishes when one of x
1
,...,x
r−1
is
constant. Then it follows that
( p
0
, p
2
,..., p
r
)
ψ = 0
since x
1
≡ 0on( p
0
, p
2
,...,p
r
). In fact, most of the faces of ∂ ¯σ
r
do not
contribute to the RHS of (6.9b) and we are left with
∂ ¯σ
r
ψ =
( p
1
, p
2
,..., p
r
)
ψ + (−1)
r
( p
0
, p
1
,..., p
r−1
)
ψ.

Since ( p
0
, p
1
,...,p
r−1
) is the standard (r − 1)-simplex (x
µ
≥ 0,
r−1
µ=1
x
µ
≤
1),onwhichx
r
= 0, the second term is
(−1)
r
( p
0
, p
1
,..., p
r−1
)
ψ = (−1)
r
¯σ
r−1
a(x
1
,...,x
r−1
, 0) dx
1
...dx
r−1
.
The first term is
( p
1
, p
2
,..., p
r
)
ψ =
( p
1
,..., p
r−1
, p
0
)
a
x
1
,...,x
r−1
, 1 −
r−1
µ=1
x
µ
dx
1
...dx
r−1
= (−1)
r−1
¯σ
r−1
a
x
1
,...,x
r−1
, 1 −
r−1
µ=1
x
µ
dx
1
...dx
r−1
where the integral domain ( p
1
,...,p
r
) has been projected along x
r
to the
( p
1
,...,p
r−1
, p
0
)-plane, preserving the orientation. Collecting these results, we
have proved (6.9b). [The reader is advised to verify this proof for m = 3using
figure 6.1.]
Exercise 6.1. Let M =
3
and ω = a dx +b dy+c dz. Show that Stokes’ theorem
is written as
S
curl ω · dS =
'
C
ω · dS (Stokes’ theorem) (6.10)
where ω = (a, b, c) and C is the boundary of a surface S. Similarly, for
ψ =
1
2
ψ
µν
dx
µ
∧ dx
ν
, show that
V
div ψ dV =
'
S
ψ ·dS (Gauss’ theorem)
where ψ
λ
= ε
λµν
ψ
µν
and S is the boundary of a volume V .
6.2 de Rham cohomology groups
6.2.1 Definitions
Definition 6.1. Let M be an m-dimensional differentiable manifold. The set of
closed r-forms is called the rth cocycle group, denoted Z
r
(M). The set of exact
r-forms is called the r th coboundary group, denoted B
r
(M). These are vector
spaces with
-coefficients. It follows from d
2
= 0thatZ
r
(M) ⊃ B
r
(M).
Exercise 6.2. Show that
(a) if ω ∈ Z
r
(M) and ψ ∈ Z
s
(M),thenω ∧ ψ ∈ Z
r+s
(M);
(b) if ω ∈ Z
r
(M) and ψ ∈ B
s
(M),thenω ∧ ψ ∈ B
r+s
(M);and
(c) if ω ∈ B
r
(M) and ψ ∈ B
s
(M),thenω ∧ψ ∈ B
r+s
(M).
Definition 6.2. The rth de Rham cohomology group is defined by
H
r
(M; ) ≡ Z
r
(M)/B
r
(M). (6.11)
If r ≤−1orr ≥ m +1, H
r
(M; ) may be defined to be trivial. In the following,
we omit the explicit quotation of
-coefficients.
Let ω ∈ Z
r
(M).Then[ω]∈H
r
(M) is the equivalence class {ω
∈
Z
r
(M)|ω
= ω + dψ, ψ ∈
r−1
(M)}. Two forms which differ by an exact
form are called cohomologous. We will see later that H
r
(M) is isomorphic to
H
r
(M). The following examples will clarify the idea of de Rham cohomology
groups.
Example 6.1. When r = 0, B
0
(M) has no meaning since there is no (−1)-form.
We d efine
−1
(M) to be empty, hence B
0
(M) = 0. Then H
0
(M) = Z
0
(M) =
{ f ∈
0
(M) = (M)|d f = 0}.IfM is connected, the condition d f = 0is
satisfied if and only if f is constant over M. Hence, H
0
(M) is isomorphic to the
vector space
,
H
0
(M)
∼
=
. (6.12)
If M has n connected components, d f = 0 is satisfied if and only if f is constant
on each connected component, hence it is specified by n real numbers,
H
0
(M)
∼
=
⊕ ⊕···⊕
, -. /
n
. (6.13)
Example 6.2. Let M =
. From example 6.1, we have H
0
( ) = .Letus
find H
1
( ) next. Let x be a coordinate of .Sincedim = 1, any one-form
ω ∈
1
( ) is closed, dω = 0. Let ω = f dx ,where f ∈ ( ). Define a function
F(x ) by
F(x ) =
x
0
f (s) ds ∈ ( ) =
0
( ).
Since dF (x )/dx = f (x), ω is an exact form,
ω = f dx =
dF(x)
dx
dx = dF.
Thus, any one-form is closed as well as exact. We have established
H
1
( ) ={0}. (6.14)
Example 6.3. Let S
1
={e
iθ
|0 ≤ θ<2π}.SinceS
1
is connected, we have
H
0
(S
1
) = . We compute H
1
(S
1
) next. Let ω = f (θ) dθ ∈
1
(S
1
).Isit
