Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

Figure 5.12. To compare a vector Y

with Y

(x)

, the latter must be transported back to

x by the differential map (σ

−ε

)

∗

Exercise 5.8. Show that

Y is also written as

Y = lim

ε→0

[Y |

− (σ

)

∗

Y |

−ε

(x)

]

= lim

ε→0

[Y |

(x)

− (σ

)

∗

Y |

Let (U,ϕ) be a chart with the coordinates x and let X = X

∂/∂x

and

Y = Y

∂/∂x

be vector ﬁelds deﬁned on U .Thenσ

(x ) has the coordinates

+ εX

(x ) and

Y |

(x)

= Y

+ ε X

(x ))e

x+ε X

[Y

(x ) + εX

(x )∂

(x )]e

x+ε X

where {e

}={∂/∂x

} is the coordinate basis and ∂

≡ ∂/∂x

. If we map this

vector deﬁned at σ

(x ) to x by (σ

−ε

)

∗

, we obtain

(x ) + εX

(x )∂

(x )]∂

− ε X

(x )]e

=[Y

(x ) + εX

(x )∂

(x )][δ

− ε∂

(x )]e

= Y

(x )e

+ ε[X

(x )∂

(x ) − Y

(x )∂

(x )]e

+ O(ε

(5.48)

From (5.47) and (5.48), we ﬁnd that

Y = (X

∂

− Y

∂

. (5.49a)

Exercise 5.9. Let X = X

∂/∂x

and Y = Y

∂/∂x

be vector ﬁelds in M.

Deﬁne the Lie bracket [X, Y ] by

[X, Y ] f = X [Y [ f ]]− Y [X[ f ]] (5.50)

where f ∈

(M). Show that [X, Y ] is a vector ﬁeld given by

∂

− Y

∂

This exercise shows that the Lie derivative of Y along X is

Y =[X, Y ].(5.49b)

[Remarks: Note that neither XY nor YX is a vector ﬁeld since they are second-

order derivatives. The combination [X, Y ] is, however, a ﬁrst-order derivative and

indeed a vector ﬁeld.]

Exercise 5.10. Show that the Lie bracket satisﬁes

(a) bilinearity

[X, c

+ c

] = c

[X, Y

]+c

[X, Y

]

+ c

, Y ] = c

, Y ]+c

, Y ]

for any constants c

and c

(b) skew-symmetry

[X, Y ]=−[YX]

[[X, Y ], Z ]+[[Z, X], Y ]+[[Y, Z], X ]=0.

Exercise 5.11. (a) Let X, Y ∈

(M) and f ∈ (M). Show that

Y = f [X, Y ]−Y [ f ]X (5.51a)

( fY) = f [X, Y ]+X [f ]Y. (5.51b)

(b) Let X, Y ∈

(M) and f : M → N. Show that

∗

[X, Y ]=[f

∗

X, f

∗

Y ]. (5.52)

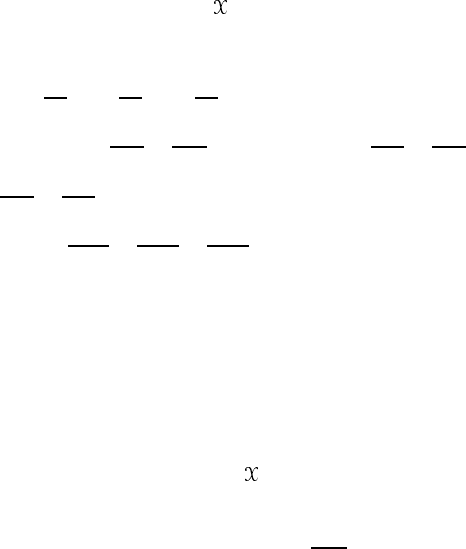
Geometrically, the Lie bracket shows the non-commutativity of two ﬂows.

This is easily observed from the following consideration. Let σ(s, x) and τ(t, x )

be two ﬂows generated by vector ﬁelds X and Y , as before, see ﬁgure 5.13. If we

move by a small parameter distance ε along the ﬂow σ ﬁrst, then by δ along τ ,

we shall be at the point whose coordinates are

(δ, σ (ε, x ))  τ

(δ, x

+ ε X

(x ))

 x

+ ε X

(x ) + δY

+ ε X

(x ))

 x

+ ε X

(x ) + δY

(x ) + εδX

(x )∂

(x ).

Figure 5.13. A Lie bracket [X, Y ] measures the failure of the closure of the parallelogram.

If, however, we move by δ along τ ﬁrst, then by ε along σ , we will be at the point

(ε, τ (δ, x))  σ

(ε, x

+ δY

(x ))

 x

+ δY

(x ) + εX

+ δY

(x ))

 x

+ δY

(x ) + εX

(x ) + εδY

(x )∂

(x ).

The difference between the coordinates of these two points is proportional to the

Lie bracket,

(δ, σ (ε, x )) − σ

(ε, τ (δ, x)) = εδ[X, Y ]

The Lie bracket of X and Y measures the failure of the closure of the

parallelogram in ﬁgure 5.13. It is easy to see

Y =[X, Y ]=0 if and only

σ(s,τ(t, x)) = τ(t,σ(s, x)). (5.53)

We may also deﬁne the Lie derivative of a one-form ω ∈ 

(M) along

X ∈

(M) by

ω ≡ lim

ε→0

[(σ

)

∗

ω|

(x)

− ω|

] (5.54)

where ω

∈ T

∗

M is ω at x.Putω = ω

. Repeating a similar analysis as

before, we obtain

(σ

)

∗

ω|

(x)

= ω

(x ) dx

+ ε[X

(x )∂

(x ) + ∂

(x )ω

(x )]dx

which leads to

ω = (X

∂

+ ∂

) dx

. (5.55)

Clearly

ω ∈ T

∗

(M), since it is a difference of two one-forms at the same point

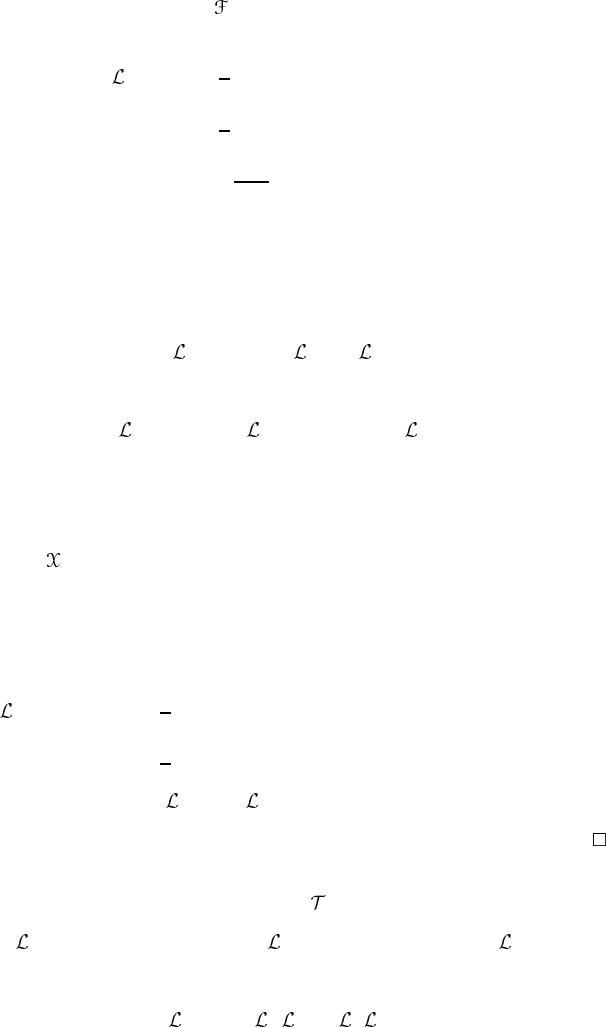
The Lie derivative of f ∈

(M) along a ﬂow σ

generated by a vector ﬁeld

X is

f ≡ lim

ε→0

[ f (σ

(x )) − f (x )]

= lim

ε→0

[ f (x

+ ε X

(x )) − f (x

)]

= X

(x )

∂ f

∂x

= X [ f ] (5.56)

which is the usual directional derivative of f along X.

The Lie derivative of a general tensor is obtained from the following

proposition.

Proposition 5.1. The Lie derivative satisﬁes

+ t

) =

(5.57a)

where t

and t

are tensor ﬁelds of the same type and

⊗ t

) = (

) ⊗ t

+ t

⊗ (

)(5.57b)

where t

and t

are tensor ﬁelds of arbitrary types.

Proof. (a) is obvious. Rather than giving the general proof of (b), which is full

of indices, we give an example whose extension to more general cases is trivial.

Take Y ∈

(M) and ω ∈ 

(M) and construct the tensor product Y ⊗ ω.Then

(Y ⊗ ω)

(x)

is mapped onto a tensor at x by the action of (σ

−ε

)

∗

⊗ (σ

)

∗

[(σ

−ε

)

∗

⊗ (σ

)

∗

](Y ⊗ ω)|

(x)

=[(σ

−ε

)

∗

Y ⊗ (σ

)

∗

ω]|

Then there follows (the Leibnitz rule):

(Y ⊗ ω) = lim

ε→0

[{(σ

−ε

)

∗

Y ⊗ (σ

)

∗

ω}|

− (Y ⊗ω)|

]

= lim

ε→0

[(σ

−ε

)

∗

Y ⊗{(σ

)

∗

ω − ω}+{(σ

−ε

)

∗

Y − Y }⊗ω]

= Y ⊗ (

ω) + (

Y ) ⊗ ω.

Extensions to more general cases are obvious.

This proposition enables us to calculate the Lie derivative of a general tensor

ﬁeld. For example, let t = t

⊗ e

∈

(M). Proposition 5.1 gives

t = X[t

]dx

⊗ e

+ t

(

) ⊗ e

+ t

⊗ (

Exercise 5.12. Let t be a tensor ﬁeld. Show that

[X,Y ]

t =

X Y

t −

Y X

t. (5.58)

5.4 Differential forms

Before we deﬁne differential forms, we examine the symmetry property of

tensors. The symmetry operation on a tensor ω ∈

r,p

(M) is deﬁned by

Pω(V

,...,V

) ≡ ω(V

P(1)

,...,V

P(r)

) (5.59)

where V

∈ T

M and P is an element of S

,thesymmetric group of order r .

Take the coordinate basis {e

}={∂/∂x

}. The component of ω in this basis is

ω(e

, e

,...,e

) = ω

...µ

The component of Pω is obtained from (5.59) as

Pω(e

, e

,...,e

) = ω

P(1)

P(2)

...µ

P(r)

For a general tensor of type (q, r), the symmetry operations are deﬁned for q

indices and r indices separately.

For ω ∈

r,p

(M),thesymmetrizer is deﬁned by

ω =



P∈S

Pω (5.60)

while the anti-symmetrizer

ω =



P∈S

sgn(P)Pω (5.61)

where sgn(P) =+1 for even permutations and −1 for odd permutations.

ω is

totally symmetric (that is, P

ω = ω for any P ∈ S

)and ω is totally anti-

symmetric (P

ω = sgn(P) ω).

5.4.1 Deﬁnitions

Deﬁnition 5.4. A differential form of order r or an r-form is a totally anti-

symmetric tensor of type (0, r).

Let us deﬁne the wedge product ∧ of r one-forms by the totally anti-

symmetric tensor product

∧dx

∧...∧dx



P∈S

sgn(P) dx

P(1)

∧dx

P(2)

∧...∧dx

P(r)

. (5.62)

For example,

∧ dx

= dx

⊗ dx

− dx

⊗ dx

∧ dx

= dx

⊗ dx

+ dx

⊗ dx

+ dx

⊗ dx

− dx

⊗ dx

− dx

⊗ dx

− dx

⊗ dx

It is readily veriﬁed that the wedge product satisﬁes the following.

(i) dx

∧ ...∧ dx

= 0 if some index µ appears at least twice.

(ii) dx

∧ ...∧ dx

= sgn(P) dx

P(1)

∧ ...∧ dx

P(r)

(iii) dx

∧ ...∧ dx

is linear in each dx

If we denote the vector space of r-forms at p ∈ M by 

(M),thesetof

r-forms (5.62) forms a basis of 

(M) andanelementω ∈ 

(M) is expanded

ω =

...µ

∧ dx

∧ ...∧ dx

(5.63)

where ω

...µ

are taken totally anti-symmetric, reﬂecting the anti-symmetry

of the basis. For example, the components of any second-rank tensor ω

µν

are

decomposed into the symmetric part σ

µν

and the anti-symmetric part α

µν

=ω

(µν)

≡

(ω

µν

+ ω

νµ

) (5.64a)

µν

=ω

[µν]

≡

(ω

µν

− ω

νµ

). (5.64b)

Observe that σ

µν

∧ dx

= 0, while α

µν

∧ dx

= ω

µν

∧ dx

Since there are



choices of the set (µ

,µ

,...,µ

) out of (1, 2,...,m)

in (5.62), the dimension of the vector space 

(M) is





(m −r )!r!

For later convenience we deﬁne 

(M) = . Clearly 

(M) = T

∗

M.If

r in (5.62) exceeds m, it vanishes identically since some index appears at least

twice in the anti-symmetrized summation. The equality



m−r

implies

dim 

(M) = dim 

m−r

(M).Since

(M) is a vector space, 

(M) is

isomorphic to 

m−r

(M) (see section 2.2).

Deﬁne the exterior product of a q-form and an r-form ∧:

(M) ×



(M) → 

q+r

(M) by a trivial extension. Let ω ∈ 

(M) and ξ ∈ 

(M),

for example. The action of the (q +r)-form ω ∧ ξ on q +r vectors is deﬁned by

(ω ∧ ξ)(V

,...,V

q+r

)

q!r!



P∈S

q+r

sgn(P)ω(V

P(1)

,...,V

P(q)

)ξ(V

P(q+1)

,...,V

P(q+r)

)

(5.65)

where V

∈ T

M.Ifq + r > m, ω ∧ ξ vanishes identically. With this product,

we deﬁne an algebra



∗

(M) ≡ 

(M) ⊕ 

(M) ⊕ ...⊕ 

(M). (5.66)

Tab le 5.1.

r-forms Basis Dimension



(M) = (M) {1} 1



(M) = T

∗

M {dx

} m



(M) {dx

∧ dx

} m(m − 1)/2



(M) {dx

∧ dx

} m(m − 1)(m −2)/6



(M) {dx

∧ dx

∧ ...dx

} 1



∗

(M) is the space of all differential forms at p and is closed under the exterior

product.

Exercise 5.13. Take the Cartesian coordinates (x , y) in

. The two-form dx ∧dy

is the oriented area element (the vector product in elementary vector algebra).

Show that, in polar coordinates, this becomes r dr ∧ dθ.

Exercise 5.14. Let ξ ∈ 

(M), η ∈ 

(M) and ω ∈ 

(M). Show that

ξ ∧ ξ = 0ifq is odd (5.67a)

ξ ∧ η = (−1)

η ∧ ξ (5.67b)

(ξ ∧ η) ∧ ω = ξ ∧ (η ∧ω). (5.67c)

We may assign an r -form smoothly at each point on a manifold M.We

denote the space of smooth r-forms on M by 

(M).Wealsodeﬁne

(M) to

be the algebra of smooth functions,

(M). In summary we have table 5.1.

5.4.2 Exterior derivatives

Deﬁnition 5.5. The exterior derivative d

is a map 

(M) → 

r+1

(M) whose

actiononanr-form

ω =

...µ

∧ ...∧ dx

is deﬁned by

ω =



∂

∂x

...µ



∧ dx

∧ ...∧ dx

. (5.68)

It is common to drop the subscript r and write simply d. The wedge product

automatically anti-symmetrizes the coefﬁcient.

Example 5.10. The r-forms in three-dimensional space are:

(i) ω

= f (x, y, z),

(ii) ω

= ω

(x , y, z) dx + ω

(x , y, z) dy + ω

(x , y, z) dz,

(iii) ω

= ω

(x , y, z) dx ∧dy +ω

(x , y, z) dy ∧dz +ω

(x , y, z) dz ∧dx

and

(iv) ω

= ω

xyz

(x , y, z) dx ∧ dy ∧ dz.

If we deﬁne an axial vector α

by ε

µνλ

νλ

, a two-form may be regarded as a

‘vector’. The Levi-Civita symbol ε

µνλ

is deﬁned by ε

P(1)P(2) P(3)

= sgn(P) and

provides the isomorphism between

(M) and 

(M). [Note that both of these

are of dimension three.]

The action of d is

(i) dω

∂ f

∂x

dx +

∂ f

∂y

dy +

∂ f

∂z

dz,

(ii) dω



∂ω

∂x

−

∂ω

∂y



dx ∧ dy +



∂ω

∂y

−

∂ω

∂z



dy ∧ dz



∂ω

∂z

−

∂ω

∂x



dz ∧ dx ,

(iii) dω



∂ω

∂x

∂ω

∂y

∂ω

∂z



dx ∧ dy ∧ dz and

(iv) dω

= 0.

Hence, the action of d on ω

is identiﬁed with ‘grad’, on ω

with ‘rot’ and on ω

with ‘div’ in the usual vector calculus.

Exercise 5.15. Let ξ ∈ 

(M) and ω ∈ 

(M). Show that

d(ξ ∧ ω) = dξ ∧ ω + (−1)

ξ ∧ dω. (5.69)

A useful expression for the exterior derivative is obtained as follows. Let us

take X = X

∂/∂x

, Y = Y

∂/∂x

∈ (M) and ω = ω

∈ 

(M).Itis

easy to see that the combination

X[ω(Y )]−Y [ω(X)]−ω([X, Y ]) =

∂ω

∂x

− X

)

is equal to dω(X, Y ), and we have the coordinate-free expression

dω(X, Y ) = X [ω(Y )]−Y [ω(X)]−ω([X, Y ]). (5.70)

For an r -form ω ∈ 

(M), this becomes

dω(X

,...,X

r+1

)



i=1

(−1)

i+1

ω(X

,...,

,...,X

r+1

)



i< j

(−1)

i+j

ω([X

, X

], X

,...,

,...,X

r+1

) (5.71)

where the entry below ˆ has been omitted. As an exercise, the reader should

verify (5.71) explicitly for r = 2.

We now prove an important formula:

= 0 (or d

r+1

= 0). (5.72)

Take

ω =

...µ

∧ ...∧ dx

∈ 

(M).

The action of d

on ω is

ω =

∂

...µ

∂x

∧ dx

∧ ...∧ dx

This vanishes identically since ∂

...µ

/∂x

∂x

is symmetric with respect to λ

and ν while dx

∧ dx

is anti-symmetric.

Example 5.11. It is known that the electromagnetic potential A = (φ, A) is a

one-form, A = A

(see chapter 10). The electromagnetic tensor is deﬁned

by F = d A and has the components







0 −E

−E

0 B

−B

0 B

−B







(5.73)

where

E =−∇φ −

∂

∂x

A and B =∇×A

as usual. Two Maxwell equations, ∇·B = 0and∂B/∂t =−∇×E follow from

the identity dF = d(dA) = 0, which is known as the Bianchi identity, while the

other set is the equation of motion derived from the Lagrangian (1.245).

Amap f : M → N induces the pullback f

∗

: T

∗

f ( p)

N → T

∗

M and

∗

is naturally extended to tensors of type (0, r); see section 5.2. Since an

r-form is a tensor of type (0, r), this applies as well. Let ω ∈ 

(N) and

let f beamapM → N. At each point f (p) ∈ N, f induces the pullback

∗

: 

f ( p)

N → 

M by

( f

∗

ω)(X

,...,X

) ≡ ω( f

∗

,..., f

∗

) (5.74)

where X

∈ T

M and f

∗

is the differential map T

M → T

f ( p)

Exercise 5.16. Let ξ,ω ∈ 

(N) and let f : M → N. Show that

d ( f

∗

ω) = f

∗

(dω) (5.75)

∗

(ξ ∧ ω) = ( f

∗

ξ) ∧( f

∗

ω). (5.76)

The exterior derivative d

induces the sequence

−→ 

(M)

−→ 

(M)

−→···

m−2

−→ 

m−1

(M)

m−1

−→ 

(M)

−→ 0 (5.77)

where i is the inclusion map 0 → 

(M). This sequence is called the de Rham

complex.Sinced

= 0, we have im d

⊂ ker d

r+1

.[Takeω ∈ 

(M).Then

ω ∈ im d

and d

r+1

ω) = 0implyd

ω ∈ ker d

r+1

.] An element of ker d

called a closed r-form, while an element of im d

r−1

is called an exact r-form.

Namely, ω ∈ 

(M) is closed if dω = 0 and exact if there exists an (r −1)-form

ψ such that ω = dψ. The quotient space ker d

/ im d

r−1

is called the r th de

Rham cohomology group which is made into the dual space of the homology

group; see chapter 6.

5.4.3 Interior product and Lie derivative of forms

Another important operation is the interior product i

: 

(M) → 

r−1

(M),

where X ∈

(M).Forω ∈ 

(M),wedeﬁne

ω(X

,...,X

r−1

) ≡ ω(X, X

,...,X

r−1

). (5.78)

For X = X

∂/∂x

and ω = (1/r!)ω

...µ

∧ ...∧ dx

we have

ω =

(r − 1)!

νµ

...µ

∧ ...∧ dx



s=1

...µ

(−1)

s−1

∧ ...∧

∧ ...∧ dx

(5.79)

where the entry below ˆ has been omitted. For example, let (x , y, z) be the

coordinates of

.Then

(dx ∧ dy) = dy, i

(dy ∧ dz) = 0, i

(dz ∧ dx ) =−dz.

The Lie derivative of a form is most neatly written with the interior product.

Let ω = ω

be a one-form. Consider the combination

(di

+ i

d)ω = d (X

) + i

[

(∂

− ∂

) dx

∧ dx

]

= (ω

∂

+ X

∂

) dx

+ X

(∂

− ∂

) dx

= (ω

∂

+ X

∂

) dx

Comparing this with (5.55), we ﬁnd that

ω = (di

+ i

d)ω. (5.80)