Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

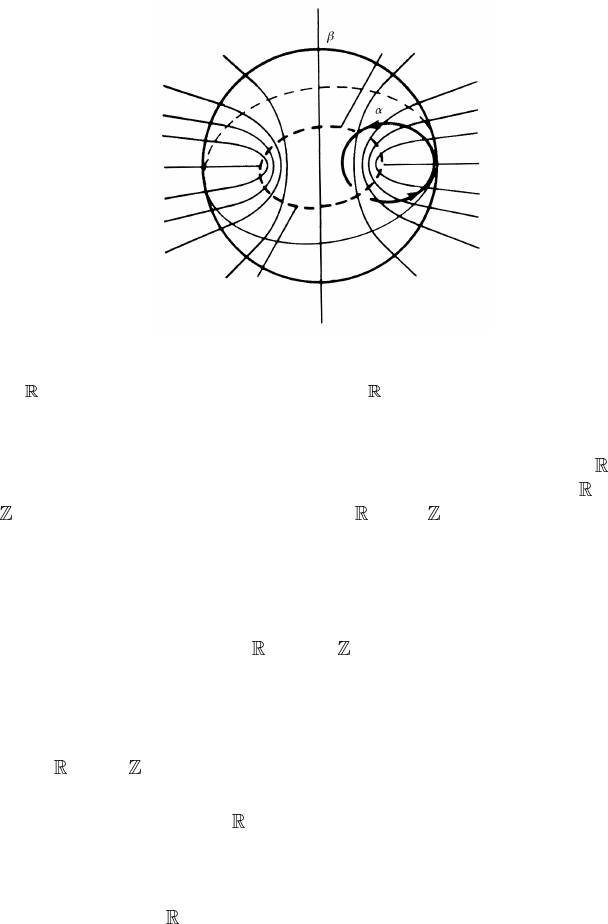
Figure 4.27. The texture of a ring defect in a nematic liquid crystal. The loop α classiﬁes

( P

) while the sphere (2-loop) β classiﬁes π

( P

a point defect, while its local structure along the ring is speciﬁed by π

( P

Figure 4.27 is an example of such a ring defect. The loop α classiﬁes π

( P

)

∼

while the sphere (2-loop) β classiﬁes π

( P

) = .

4.9.4 Higher dimensional texture

The third homotopy group π(

)

∼

leads to an interesting singularity-

free texture in a three-dimensional medium of nematic liquid crystal. Suppose

the director ﬁeld approaches an asymptotic conﬁguration, say n = (1, 0, 0)

as |r|→∞. Then the medium is effectively compactiﬁed into the three-

dimensional sphere S

and the topological structure of the texture is classiﬁed

by π

( P

)

∼

. What is the texture corresponding to a non-trivial element of

the homotopy group?

An arbitrary rotation in

is speciﬁed by a unit vector e, around which the

rotation is carried out, and the rotation angle α. It is possible to assign a ‘vector’

 = αe to this rotation. It is not exactly a vector since  = π e and − =−π e

are the same rotation and hence should be identiﬁed. Therefore,  belongs to the

real projective space

. Suppose we take n

= (1, 0, 0)

as a standard director.

Then an arbitrary director conﬁguration is speciﬁed by rotating n

around some

axis e by an angle α: n = R(e,α)n

,whereR(e,α)is the corresponding rotation

matrix in SO(3). Suppose a texture ﬁeld is given by applying the rotation

αe(r) = f (r )ˆr (4.68)

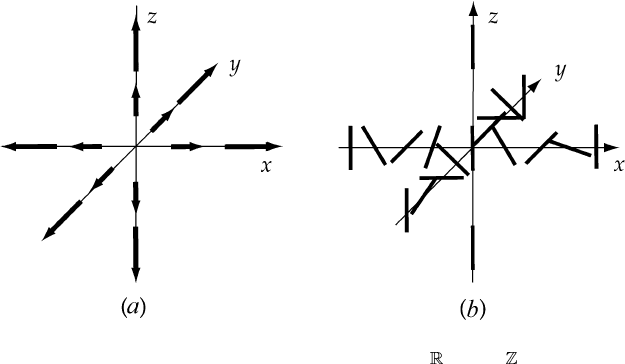
Figure 4.28. The texture of the non-trivial element of π

( P

)

∼

.(a)showsthe

rotation ‘vector’ αe. The length α approaches π as |r|→∞.(b) shows the corresponding

director ﬁeld.

to n

,whereˆr is the unit vector in the direction of the position vector r and

f (r) =



0 r = 0

π r →∞.

Figure 4.28 shows the director ﬁeld of this texture. Note that although there

is no singularity in the texture, it is impossible to ‘wind off’ this to a uniform

conﬁguration.

4.10 Textures in superﬂuid

He-A

4.10.1 Superﬂuid

He-A

Here comes the last and most interesting example. Before 1972 the only example

of the BCS superﬂuid was the conventional superconductor (apart from indirect

observations of superﬂuid neutrons in neutron stars). Figure 4.29 is the phase

diagram of superﬂuid

He without an external magnetic ﬁeld. From NMR and

other observations, it turns out that the superﬂuid is in the spin-triplet p-wave

state. Instead of the ﬁeld operators (see (4.65b)), we deﬁne the order parameter

in terms of the creation and annihilation operators. The most general form of the

triplet superﬂuid order parameter is

c

α,k

β,−k

∝



µ=1

(iσ

)

αβ

(k) (4.69a)

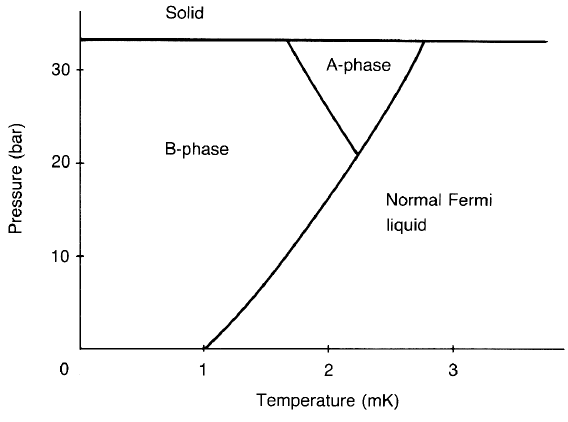
Figure 4.29. The phase diagram of superﬂuid

He.

where α and β are spin indices. The Cooper pair forms in the p-wave state hence

(k) is proportional to Y

∼ k

(k) =



i=1



µi

. (4.69b)

The bulk energy has several minima. The absolute minimum depends on the

pressure and the temperature. We are particularly interested in the A phase in

ﬁgure 4.29.

The A-phase order parameter takes the form

µi

= d

(

+ i

)

(4.70)

where d is a unit vector along which the spin projection of the Cooper pair

vanishes and (

, 

) is a pair of orthonormal unit vectors. The vector d takes

its value in S

.Ifwedeﬁnel ≡ 

× 

, the triad (

, 

, l) forms an

orthonormal frame at each point of the medium. Since any orthonormal frame

can be obtained from a standard orthonormal frame (e

, e

) by an application

of a three-dimensional rotation matrix, we conclude that the order parameter of

He-A is S

× SO(3). The vector l introduced here is the axis of the angular

momentum of the Cooper pair.

For simplicity, we neglect the variation of the

d-vector. [In fact,

d is locked

along

l due to the dipole force.] The order parameter assumes the form

= 

(



)

(4.71)

where



and

l ≡



form an orthonormal frame at each point of

the medium. Let us take a standard orthonormal frame (e

, e

). The frame

(



l) is obtained by applying an element g ∈ SO(3) to the standard frame,

g : (e

, e

) → (



l). (4.72)

Since g depends on the coordinate x, the conﬁguration (



(x ),



(x ),

l(x))

deﬁnes a map ψ : X → SO(3) as x → g(x ).Themapψ is called the texture

of a superﬂuid

He.

The relevant homotopy groups for classifying defects in

superﬂuid

He-A are π

(SO(3)).

If a container is ﬁlled with

He-A, the boundary poses certain conditions on

the texture. The vector

l is understood as the direction of the angular momentum

of the Cooper pair. The pair should rotate in the plane parallel to the boundary

wall, thus

l should be perpendicular to the wall. [Remark: If the wall is diffuse,

the orbital motion of Cooper pairs is disturbed and there is a depression in the

amplitude of the order parameter in the vicinity of the wall. We assume, for

simplicity, that the wall is specularly smooth so that Cooper pairs may execute

orbital motion with no disturbance.] There are several kinds of free energy and

the texture is determined by solving the Euler–Lagrange equation derived from

the total free energy under given boundary conditions.

Reviews on superﬂuid

He are found in Anderson and Brinkman (1975),

Leggett (1975) and Mermin (1978).

4.10.2 Line defects and non-singular vortices in

He-A

The fundamental group of SO(3)

∼

is π

( P

)

∼

{0, 1}.

Textures which belong to class 0 can be continuously deformed into the uniform

conﬁguration. Conﬁgurations in class 1 are called disgyrations and have

been analysed by Maki and Tsuneto (1977) and Buchholtz and Fetter (1977).

Figure 4.30 describes these disgyrations in their lowest free energy conﬁgurations.

A remarkable property of

is the addition 1 + 1 = 0; the coalescence of

two disgyrations produces a trivial texture. By merging two disgyrations, we may

construct a texture that looks like a vortex of double vorticity (homotopy class

‘2’) without a singular core; see ﬁgure 4.31(a). It is easy to verify that the image

of the loop α traverses

twice while that of the smaller loop β may be shrunk

to a point. This texture is called the Anderson–Toulouse vortex (Anderson and

Toulouse 1977). Mermin and Ho (1976) pointed out that if the medium is in a

cylinder, the boundary imposes the condition

l ⊥ (boundary) and the vortex is

cut at the surface, see ﬁgure 4.31(b)(theMermin–Ho vortex).

The name ‘texture’ is, in fact, borrowed from the order-parameter conﬁguration in liquid crystals,

see section 4.9.

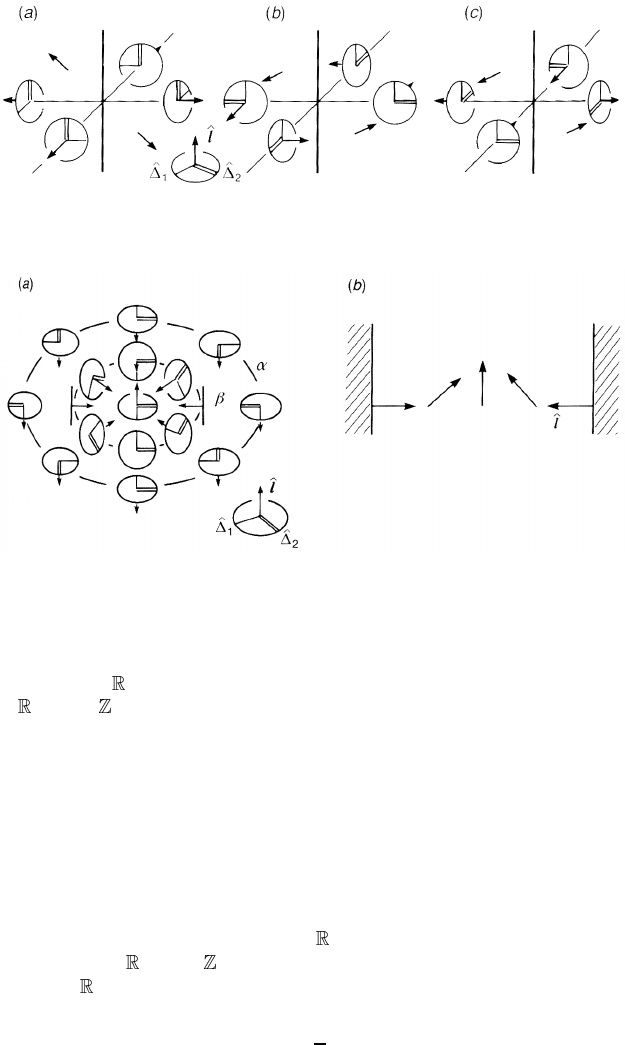
Figure 4.30. Disgyrations in

He-A.

Figure 4.31. The Anderson–Toulouse vortex (a) and the Mermin–Ho vortex (b). In (b)the

boundary forces

l to be perpendicular to the wall.

Since π

( P

)

∼

{e}, there are no point defects in

He-A. However,

( P

)

∼

introduces a new type of pointlike structure called the Shankar

monopole, which we will study next.

4.10.3 Shankar monopole in

He-A

Shankar (1977) pointed out that there exists a pointlike singularity-free object

He-A. Consider an inﬁnite medium of

He-A. We assume the medium is

asymptotically uniform, that is, (



l) approaches a standard orthonormal

frame (e

, e

) as |x |→∞. Since all the points far from the origin are mapped

to a single point, we have compactiﬁed

to S

. Then the texture is classiﬁed

according to π

( P

) = . Let us specify an element of SO(3) by a ‘vector’

 = θ n in

as before (example 4.12). Shankar (1977) proposed a texture,

(r) =

· f (r) (4.73)

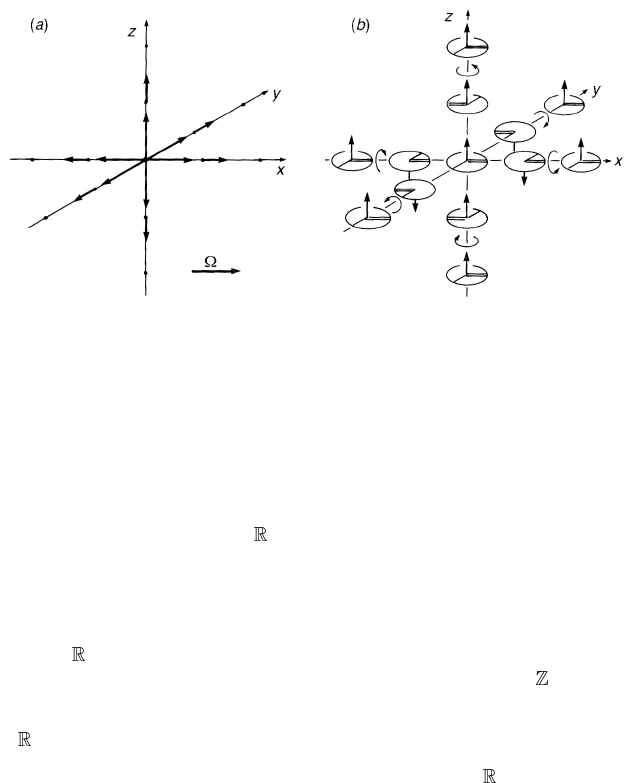
Figure 4.32. The Shankar monopole: (a) shows the ‘vectors’ (r) and (b)showsthetriad

(



l). Note that as |r|→∞the triad approaches the same conﬁguration.

where f (r) is a monotonically decreasing function such that

f (r) =



2π r = 0

0 r =∞.

(4.74)

We formally extend the radius of

to 2π and deﬁne the rotation angle modulo

2π. This texture is called the Shankar monopole, see ﬁgure 4.32(a). At ﬁrst sight

it appears that there is a singularity at the origin. Note, however, that the length

of  is 2π there and it is equivalent to the unit element of SO(3). Figure 4.32(b)

describes the triad ﬁeld. Since (r) = 0asr →∞, irrespective of the direction,

the space

is compactiﬁed to S

. As we scan the whole space, (r) sweeps

SO(3) twice and this texture corresponds to class 1 of π

(SO(3))

∼

Exercise 4.10. Sketch the Shankar monopole which belongs to the class −1of

( P

). [You cannot simply reverse the arrows in ﬁgure 4.32.]

Exercise 4.11. Consider classical Heisenberg spins deﬁned in

, see section 4.8.

Suppose spins take the asymptotic value

n(x) → e

|x|≥L (4.75)

for the total energy to be ﬁnite, see ﬁgure 4.20. Show that the extended objects in

this system are classiﬁed by π

). Sketch examples of spin conﬁgurations for

the classes −1and+2.

Problems

4.1 Show that the n-sphere S

is a deformation retract of punctured Euclidean

space R

n+1

−{0}. Find a retraction.

4.2 Let D

be the two-dimensional closed disc and S

= ∂ D

be its boundary.

Let f : D

→ D

be a smooth map. Suppose f has no ﬁxed points, namely

f ( p) = p for any p ∈ D

. Consider a semi-line starting at p through f ( p) (this

semi-line is always well deﬁned if p = f ( p)). The line crosses the boundary at

some point q ∈ S

. Then deﬁne

f : D

→ S

f ( p) = q.Useπ

) =

and π

) ={0} to show that such an

f does not exist and hence, that f must

have ﬁxed points. [Hint: Show that if such an

f existed, D

and S

would be of

the same homotopy type.] This is the two-dimensional version of the Brouwer

ﬁxed-point theorem.

4.3 Construct a map f : S

→ S

which belongs to the elements 0 and 1 of

)

∼

. See also example 9.9.

MANIFOLDS

Manifolds are generalizations of our familiar ideas about curves and surfaces to

arbitrary dimensional objects. A curve in three-dimensional Euclidean space is

parametrized locally by a single number t as (x(t), y(t), z(t)), while two numbers

u and v parametrize a surface as (x(u,v),y(u,v),z(u,v)). A curve and a surface

are considered locally homeomorphic to

and

, respectively. A manifold,

in general, is a topological space which is homeomorphic to

locally;itmay

be different from

globally. The local homeomorphism enables us to give

each point in a manifold a set of m numbers called the (local) coordinate. If a

manifold is not homeomorphic to

globally, we have to introduce several local

coordinates. Then it is possible that a single point has two or more coordinates.

We require that the transition from one coordinate to the other be smooth.As

we will see later, this enables us to develop the usual calculus on a manifold.

Just as topology is based on continuity, so the theory of manifolds is based on

smoothness.

Useful references on this subject are Crampin and Pirani (1986), Matsushima

(1972), Schutz (1980) and Warner (1983). Chapter 2 and appendices B and C of

Wald (1984) are also recommended. Flanders (1963) is a beautiful introduction

to differential forms. Sattinger and Weaver (1986) deals with Lie groups and Lie

algebras and contains many applications to problems in physics.

5.1 Manifolds

5.1.1 Heuristic introduction

To clarify these points, consider the usual sphere of unit radius in

.We

parametrize the surface of S

, among other possibilities, by two coordinate

systems—polar coordinates and stereographic coordinates. Polar coordinates θ

and φ are usually deﬁned by (ﬁgure 5.1)

x = sin θ cos φ y = sin θ sin φ z = cos θ, (5.1)

where φ runs from 0 to 2π and θ from 0 to π. They may be inverted on the sphere

to yield

θ = tan

−1



+ y

φ = tan

−1

. (5.2)

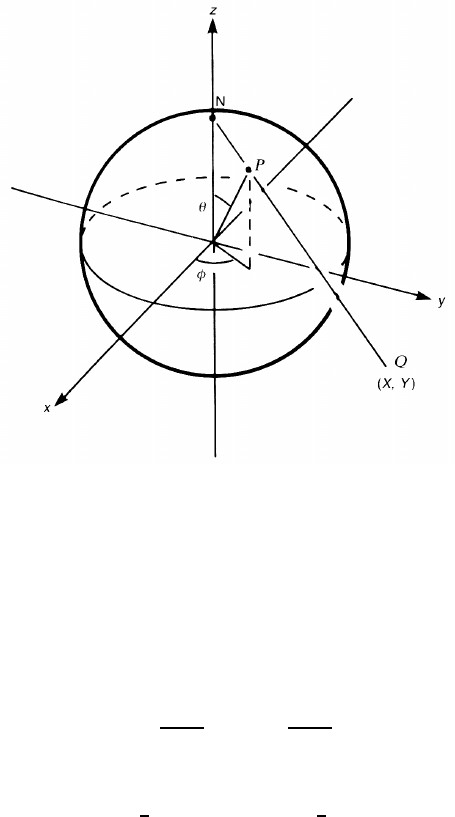
Figure 5.1. Polar coordinates (θ , φ) and stereographic coordinates (X, Y ) of a point P on

the sphere S

Stereographic coordinates, however, are deﬁned by the projection from the North

Pole onto the equatorial plane as in ﬁgure 5.1. First, join the North Pole (0, 0, 1)

to the point P(x, y, z) on the sphere and then continue in a straight line to

the equatorial plane z = 0 to intersect at Q(X, Y, 0).ThenX and Y are the

stereographic coordinates of P.Weﬁnd

X =

1 − z

Y =

1 − z

. (5.3)

The two coordinate systems are related as

X = cot

θ cos φ Y = cot

θ sin φ. (5.4)

Of course, other systems, polar coordinates with different polar axes or

projections from different points on S

, could be used. The coordinates on the

sphere may be kept arbitrary until some speciﬁc calculation is to be carried out.

[The longitude is historically measured from Greenwich. However, there is no

reason why it cannot be measured from New York or Kyoto.] This arbitrariness

of the coordinate choice underlies the theory of manifolds: all coordinate systems

are equally good. It is also in harmony with the basic principle of physics: a

physical system behaves in the same way whatever coordinates we use to describe

it.

Another point which can be seen from this example is that no coordinate

system may be usable everywhere at once. Let us look at the polar coordinates

on S

. Take the equator (θ =

π) for deﬁniteness. If we let φ range from 0 to

2π, then it changes continuously as we go round the equator until we get all the

way to φ = 2π.Theretheφ-coordinate has a discontinuity from 2π to 0 and

nearby points have quite different φ-values. Alternatively we could continue φ

through 2π. Then we will encounter another difﬁculty: at each point we must

have inﬁnitely many φ-values, differing from one another by an integral multiple

of 2π. A further difﬁculty arises at the poles, where φ is not determined at all.

[An explorer on the Pole is in a state of timelessness since time is deﬁned by the

longitude.] Stereographic coordinates also have difﬁculties at the North Pole or

at any projection point that is not projected to a point on the equatorial plane; and

nearby points close to the Pole have widely different stereographic coordinates.

Thus, we cannot label the points on the sphere with a single coordinate

system so that both of the following conditions are satisﬁed.

(i) Nearby points always have nearby coordinates.

(ii) Every point has unique coordinates.

Note, however, that there are inﬁnitely many ways to introduce coordinates that

satisfy these requirements on a part of S

. We may take advantage of this fact to

deﬁne coordinates on S

: introduce two or more overlapping coordinate systems,

each covering a part of the sphere whose points are to be labelled so that the

following conditions hold.



) Nearby points have nearby coordinatcs in at least one coordinate system.

(ii



) Every point has unique coordinates in each system that contains it.

For example, we may introduce two stereographic coordinates on S

, one a

projection from the North Pole, the other from the South Pole. Are these

conditions (i



)and(ii



) enough to develop sensible theories of the manifold? In

fact, we need an extra condition on the coordinate systems.

(iii) If two coordinate systems overlap, they are related to each other in a

sufﬁciently smooth way.

Without this condition, a differentiable function in one coordinate system

may not be differentiable in the other system.

5.1.2 Deﬁnitions

Deﬁnition 5.1. M is an m-dimensional differentiable manifold if

(i) M is a topological space;

(ii) M is provided with a family of pairs {(U

,ϕ

)};

(iii) {U

} is a family of open sets which covers M,thatis,∪

= M. ϕ

is a

homeomorphism from U

onto an open subset U



(ﬁgure 5.2); and