Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.


where T
1
and T
2
are tensor fields of arbitrary types. Equation (7.22) is also true
when some of the indices are contracted. With these requirements, we compute
the covariant derivative of a one-form ω ∈
1
(M).Sinceω,Y ∈ (M) for
Y ∈
(M), we should have
X[ω, Y ] = ∇
X
[ω,Y ] = ∇
X
ω, Y +ω, ∇
X
Y .
Writing down both sides in terms of the components we find
(∇
X
ω)
ν
= X
µ
∂
µ
ω
ν
− X
µ
λ
µν
ω
λ
. (7.23)
In particular, for X = e
µ
,wehave
(∇
µ
ω)
ν
= ∂
µ
ω
ν
−
λ
µν
ω
λ
. (7.24)
For ω = dx
ν
, we obtain (cf (7.14))
∇
µ
dx
ν
=−
ν
µλ
dx
λ
. (7.25)
It is easy to generalize these results as
∇
ν
t
λ
1
...λ
p
µ
1
...µ
q
= ∂
ν
t
λ
1
...λ
p
µ
1
...µ
q
+
λ
1
νκ
t
κλ
2
...λ
p
µ
1
...µ
q
+···
+
λ
p
νκ
t
λ
1
...λ
p−1
κ
µ
1
...µ
q
−
κ
νµ
1
t
λ
1
...λ
p
κµ
2
...µ
q
−···
−
κ
νµ
q
t
λ
1
...λ
p
µ
1
...µ
q−1
κ
. (7.26)
Exercise 7.4. Let g be a metric tensor. Verify that
(∇
ν
g)
λµ
= ∂
ν
g
λµ
−
κ
νλ
g
κµ
−
κ
νµ
g
λκ
. (7.27)
7.2.5 The transformation properties of connection coefficients
Introduce another chart (V,ψ) such that U ∩ V =∅, whose coordinates are
y = ψ(p).Let{e
µ
}={∂/∂x
µ
} and { f
α
}={∂/∂y
α
} be bases of the respective
coordinates. Denote the connection coefficients with respect to the y-coordinates
by
(
α
βγ
. The basis vector f
α
satisfies
∇
f
α
f
β
=
(
γ
αβ
f
γ
. (7.28)
If we write f
α
= (∂ x
µ
/∂y
α
)e
µ
, the LHS becomes
∇
f
α
f
β
=∇
f
α
∂x
µ
∂y
β
e
µ
=
∂
2
x
µ
∂y
α
∂y
β
e
µ
+
∂x
λ
∂y
α
∂x
µ
∂y
β
∇
e
λ
e
µ
=
∂
2
x
ν
∂y
α
∂y
β
+
∂x
λ
∂y
α
∂x
µ
∂y
β
ν
λµ
e
ν
.

Since the RHS of (7.28) is equal to
(
γ
αβ
(∂x
ν
/∂y
γ
)e
ν
, the connection coefficients
must transform as
(
γ
αβ
=
∂x
λ
∂y
α
∂x
µ
∂y
β
∂y
γ
∂x
ν
ν
λµ
+
∂
2
x
ν
∂y
α
∂y
β
∂y
γ
∂x
ν
. (7.29)
The reader should verify that this transformation rule indeed makes ∇
X
Y a vector,
namely
(
X
α
(
(
∂
α
(
Y
γ
+
(
γ
αβ
(
Y
β
) f
γ
= X
λ
(∂
λ
Y
ν
+
ν
λµ
Y
ν
)e
ν
.
In the literature, connection coefficients are often defined as objects which
transform as (7.29). From our viewpoint, however, they must transform according
to (7.29) to make ∇
X
Y independent of the coordinate chosen.
Exercise 7.5. Let be an arbitrary connection coefficient. Show that
λ
µν
+t
λ
µν
is another connection coefficient provided that t
λ
µν
is a tensor field. Conversely,
suppose
λ
µν
and
¯
λ
µν
are connection coefficients. Show that
λ
µν
−
¯
λ
µν
is a
component of a tensor of type (1, 2).
7.2.6 The metric connection
So far we have left arbitrary. Now that our manifold is endowed with a metric,
we may put reasonable restrictions on the possible form of connections. We
demand that the metric g
µν
be covariantly constant, that is, if two vectors X
and Y are parallel transported along any curve, then the inner product between
them remains constant under parallel transport. [In example 7.1, we have already
assumed this reasonable condition.] Let V be a tangent vector to an arbitrary
curve along which the vectors are parallel transported. Then we have
0 =∇
V
[g(X, Y )]=V
κ
[(∇
κ
g)(X, Y ) + g(∇
κ
X, Y ) + g(X, ∇
κ
Y )]
= V
κ
X
µ
Y
ν
(∇
κ
g)
µν
where we have noted that ∇
κ
X =∇
κ
Y = 0. Since this is true for any curves and
vectors, we must have
(∇
κ
g)
µν
= 0 (7.30a)
or, from exercise 7.4,
∂
λ
g
µν
−
κ
λµ
g
κν
−
κ
λν
g
κµ
= 0. (7.30b)
If (7.30a) is satisfied, the affine connection ∇ is said to be metric compatible or
simply a metric connection. We will deal with metric connections only. Cyclic
permutations of (λ, µ, ν) yield
∂
µ
g
νλ
−
κ
µν
g
κλ
−
κ
µλ
g
κν
= 0 (7.30c)
∂
ν
g
λµ
−
κ
νλ
g
κµ
−
κ
νµ
g
κλ
= 0. (7.30d)
The combination −(7.30b) + (7.30c) + (7.30d) yields
−∂
λ
g
µν
+ ∂
µ
g
νλ
+ ∂
ν
g
λµ
+ T
κ
λµ
g
κν
+ T
κ
λν
g
κµ
− 2
κ
(µν)
g
κλ
= 0 (7.31)
where T
κ
λµ
≡ 2
κ
[λµ]
≡
κ
λµ
−
κ
µλ
and
κ
(µν)
≡
1
2
(
κ
νµ
+
κ
µν
).The
tensor T
κ
λµ
is anti-symmetric with respect to the lower indices T
κ
λµ
=−T
κ
µλ
and called the torsion tensor, see exercise 7.6. The torsion tensor will be studied
in detail in the next section. Equation (7.31) is solved for
κ
(µν)
to yield
κ
(µν)
=
κ
µν
+
1
2
T
ν
κ
µ
+ T
µ
κ
ν
(7.32)
where
7
κ
µν
8
are the Christoffel symbols defined by
κ
µν
=
1
2
g
κλ
∂
µ
g
νλ
+ ∂
ν
g
µλ
− ∂
λ
g
µν
. (7.33)
Finally, the connection coefficient is given by
κ
µν
=
κ
(µν)
+
κ
[µν]
=
κ
µν
+
1
2
(T
ν
κ
µ
+ T
µ
κ
ν
+ T
κ
µν
). (7.34)
The second term of the last expression of (7.34) is called the contorsion, denoted
by K
κ
µν
:
K
κ
µν
≡
1
2
(T
κ
µν
+ T
µ
κ
ν
+ T
ν
κ
µ
). (7.35)
If the torsion tensor vanishes on a manifold M, the metric connection
∇ is called the Levi-Civita connection. Levi-Civita connections are natural
generalizations of the connection defined in the classical geometry of surfaces,
see section 7.4.
Exercise 7.6. Show that T
κ
µν
obeys the tensor transformation rule. [Hint:Use
(7.29).] Show also that K
κ
[µν]
=
1
2
T
κ
µν
and K
κµν
=−K
νµκ
where K
κµν
=
g
κλ
K
λ
µν
.
7.3 Curvature and torsion
7.3.1 Definitions
Since is not a tensor, it cannot have an intrinsic geometrical meaning as
a measure of how much a manifold is curved. For example, the connection
coefficients in example 7.1 vanish if the Cartesian coordinate is employed while
they do not in polar coordinates. As intrinsic objects, we define the torsion tensor
T :
(M) ⊗ (M) → (M) and the Riemann curvature tensor (or Riemann
tensor) R :
(M) ⊗ (M) ⊗ (M) → (M) by
T (X, Y ) ≡∇
X
Y −∇
Y
X −[X, Y ] (7.36)
R(X, Y, Z) ≡∇
X
∇
Y
Z −∇
Y
∇
X
Z −∇
[X,Y ]
Z. (7.37)
It is common to write R(X, Y )Z instead of R(X, Y, Z ),sothatR looks like an
operator acting on Z . Clearly, they satisfy
T (X, Y ) =−T (Y, X), R(X, Y )Z =−R(Y, X )Z. (7.38)
At first sight, T and R seem to be differential operators and it is not obvious that
they are multilinear objects. We prove the tensorial property of R,
R( fX, gY )hZ = f ∇
X
{g∇
Y
(hZ)}−g∇
Y
{ f ∇
X
(hZ)}−fX[g]∇
Y
(hZ)
+ gY[ f ]∇
X
(hZ) − fg∇
[X,Y ]
(hZ)
= fg∇
X
{Y [h]Z + h∇
Y
Z}−gf∇
Y
{X [h]Z + h∇
X
Z}
− fg[X, Y ][h]Z − fgh∇
[X,Y ]
Z
= fgh{∇
X
∇
Y
Z −∇
Y
∇
X
Z −∇
[X,Y ]
Z}
= fgh R(X, Y )Z.
Now it is easy to see that R satisfies
R(X, Y )Z = X
λ
Y
µ
Z
ν
R(e
λ
, e
µ
)e
ν
(7.39)
which verifies the tensorial property of R.SinceR maps three vector fields to a
vector field, it is a tensor field of type (1, 3).
Exercise 7.7. Show that T defined by (7.36) is multilinear,
T (X, Y ) = X
µ
Y
ν
T (e
µ
, e
ν
) (7.40)
and hence a tensor field of type (1, 2).
Since T and R are tensors, their operations on vectors are obtained once their
actions on the basis vectors are known. With respect to the coordinate basis {e
µ
}
and the dual basis {dx
µ
}, the components of these tensors are given by
T
λ
µν
=dx
λ
, T (e
µ
, e
ν
)=dx
λ
, ∇
µ
e
ν
−∇
ν
e
µ
=dx
λ
,
η
µν
e
η
−
η
νµ
e
η
=
λ
µν
−
λ
νµ
(7.41)
and
R
κ
λµν
=dx
κ
, R(e
µ
, e
ν
)e
λ
=dx
κ
, ∇
µ
∇
ν
e
λ
−∇
ν
∇
µ
e
λ
=dx
κ
, ∇
µ
(
η
νλ
e
η
) −∇
ν
(
η
µν
e
η
)
=dx
κ
,(∂
µ
η
νλ
)e
η
+
η
νλ
ξ
µη
e
ξ
− (∂
ν
η
µλ
)e
η
−
η
µλ
ξ
νη
e
ξ
= ∂
µ
κ
νλ
− ∂
ν
κ
µλ
+
η
νλ
κ
µη
−
η
µλ
κ
νη
. (7.42)
We readily find (cf (7.38))
T
λ
µν
=−T
λ
νµ
R
κ
λµν
=−R
κ
λνµ
. (7.43)
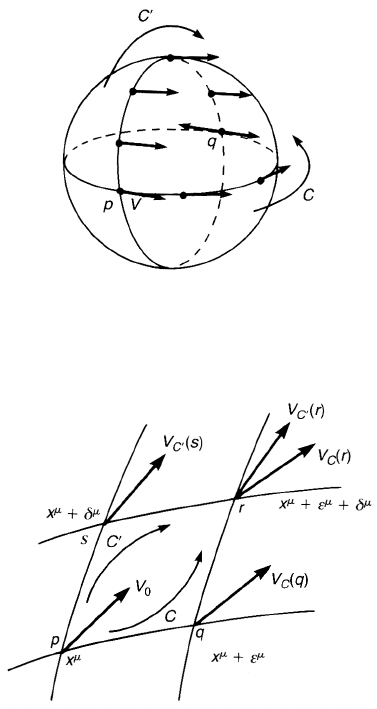
Figure 7.2. It is natural to define V parallel transported along a great circle if the angle V
makes with the great circle is kept fixed. If V at p is parallel transported along great circles
C and C
, the resulting vectors at q point in opposite directions.
Figure 7.3. A vector V
0
at p is parallel transported along C and C
to yield V
C
(r) and
V
C
(r) at r. The curvature measures the difference between two vectors.
7.3.2 Geometrical meaning of the Riemann tensor and the torsion tensor
Before we proceed further, we examine the geometrical meaning of these tensors.
We consider the Riemann tensor first. A crucial observation is that if we parallel
transport a vector V at p to q along two different curves C and C
, the resulting
vectors at q are different in general (figure 7.2). If, however, we parallel transport
a vector in a Euclidean space, where the parallel transport is defined in our
usual sense, the resulting vector does not depend on the path along which it
has been parallel transported. We expect that this non-integrability of parallel
transport characterizes the intrinsic notion of curvature, which does not depend
on the special coordinates chosen. Let us take an infinitesimal parallelogram
pqrs whose coordinates are {x
µ
}, {x
µ
+ ε
µ
}, {x
µ
+ ε
µ
+ δ
µ
} and {x
µ
+ δ
µ
}
respectively, ε
µ
and δ
µ
being infinitesimal (figure 7.3). If we parallel transport
a vector V
0
∈ T
p
M along C = pqr,wewillhaveavectorV
C
(r) ∈ T
r
M.The
vector V
0
parallel transported to q along C is
V
µ
C
(q) = V
µ
0
− V
κ
0
µ
νκ
( p)ε
ν
.
Then V
µ
C
(r) is given by
V
µ
C
(r) = V
µ
C
(q) − V
κ
C
(q)
µ
νκ
(q)δ
ν
= V
µ
0
− V
κ
0
µ
νκ
ε
ν
−[V
κ
0
− V
ρ
0
κ
ζρ
( p)ε
ζ
]
×[
µ
νκ
( p) + ∂
λ
µ
νκ
( p)ε
λ
]δ
ν
V
µ
0
− V
κ
0
µ
νκ
( p)ε
ν
− V
κ
0
µ
νκ
( p)δ
ν
− V
κ
0
[∂
λ
µ
νκ
( p) −
ρ
λκ
( p)
µ
νρ
( p)]ε
λ
δ
ν
where we have kept terms of up to order two in ε and δ. Similarly, parallel
transport of V
0
along C
= psr yields another vector V
C
(r) ∈ T
r
M,givenby
V
µ
C
(r) V
µ
0
− V
κ
0
µ
νκ
( p)δ
ν
− V
κ
0
µ
νκ
( p)ε
ν
− V
κ
0
[∂
ν
µ
λκ
( p) −
ρ
νκ
( p)
µ
λρ
( p)]ε
λ
δ
ν
.
The two vectors at r differ by
V
C
(r) − V
C
(r) = V
κ
0
[∂
λ
µ
νκ
( p) − ∂
ν
µ
λκ
( p)
−
ρ
λκ
( p)
µ
νρ
( p) +
ρ
νκ
( p)
µ
λρ
( p)]ε
λ
δ
ν
= V
κ
0
R
µ
κλν
ε
λ
δ
ν
. (7.44)
We next look at the geometrical meaning of the torsion tensor. Let p ∈ M
be a point whose coordinates are {x
µ
}.LetX = ε
µ
e
µ
and Y = δ
µ
e
µ
be
infinitesimal vectors in T
p
M. If these vectors are regarded as small displacements,
they define two points q and s near p, whose coordinates are {x
µ
+ ε
µ
} and
{x
µ
+ δ
µ
} respectively (figure 7.4). If we parallel transport X along the line ps,
we obtain a vector sr
1
whose component is ε
µ
− ε
λ
µ
νλ
δ
ν
. The displacement
vector connecting p and r
1
is
pr
1
= ps + sr
1
= δ
µ
+ ε
µ
−
µ
νλ
ε
λ
δ
ν
.
Similarly, the parallel transport of δ
µ
along pq yields a vector
pr
2
= pq + qr
2
= ε
µ
+ δ
µ
−
µ
λν
ε
λ
δ
ν
.
In general, r
1
and r
2
do not agree and the difference is
r
2
r
1
= pr
2
− pr
1
= (
µ
νλ
−
µ
λν
)ε
λ
δ
ν
= T
µ
νλ
ε
λ
δ
ν
. (7.45)
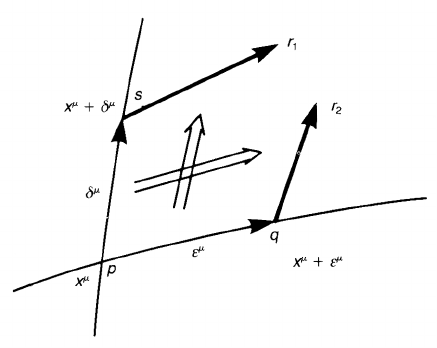
Figure 7.4. The vector qr
2
(sr
1
) is the vector ps ( pq) parallel transported to q (s). In
general, r
1
= r
2
and the torsion measures the difference r
2
r
1
.
Thus, the torsion tensor measures the failure of the closure of the parallelogram
made up of the small displacement vectors and their parallel transports.
Example 7.2. Suppose we are navigating on the surface of the Earth. We define a
vector to be parallel transported if the angle between the vector and the latitude is
kept fixed during the navigation. [Remarks: This definition of parallel transport
is not the usual one. For example, the geodesic is not a great circle but a straight
line on Mercator’s projection. See example 7.5.] Suppose we navigate along
a small quadrilateral pqrs made up of latitudes and longitudes (figure 7.5(a)).
We parallel transport a vector at p along pqr and psr, separately. According
to our definition of parallel transport, two vectors at r should agree, hence the
curvature tensor vanishes. To find the torsion, we parametrize the points p, q, r
and s as in figure 7.5(b). We find the torsion by evaluating the difference between
pr
1
and pr
2
as in (7.45). If we parallel transport the vector pq along ps,we
obtain a vector sr
1
, whose length is R sin θdφ. However, a parallel transport
of the vector ps along pq yields a vector qr
2
= qr.Sincesr has a length
R sin(θ − dθ)dφ R sin θ dφ − R cos θ dθ dφ,wefindthatr
1
r
2
has a length
R cos θ dθ dφ.Sincer
1
r
2
is parallel to −∂/∂φ, the connection has a torsion
T
φ
θφ
, see (7.45). From g
φφ
= R
2
sin
2
θ,wefindthatr
1
r
2
has components
(0, −cot θ dθ dφ). Since the φ-component of r
1
r
2
is equal to T
φ
θφ
dθdφ,we
obtain T
φ
θφ
=−cot θ.
Note that the basis {∂/∂θ, ∂/∂φ} is not well defined at the poles. It is known
that the sphere S
2
does not admit two vector fields which are linearly independent
everywhere on S
2
. Any vector field on S
2
must vanish somewhere on S
2
and

Figure 7.5. (a) If a vector makes an angle α with the longitude at p, this angle is kept fixed
during parallel transport. (b) The vector sr
1
(qr
2
) is the vector pq (ps) parallel transported
to s (q). The torsion does not vanish.
hence cannot be linearly independent of the other vector field there. If an m-
dimensional manifold M admits m vector fields which are linearly independent
everywhere, M is said to be parallelizable. On a parallelizable manifold, we
can use these m vector fields to define a tangent space at each point of M.A
vector V
p
∈ T
p
M is defined to be parallel to V
q
∈ T
q
M if all the components of
V
p
at T
p
M are equal to those of V
q
at T
q
M. Since the vector fields are defined
throughout M, this parallelism should be independent of the path connecting p
and q, hence the Riemann curvature tensor vanishes although the torsion tensor
may not in general. For S
m
, this is possible only when m = 1, 3 and 7, which is
closely related to the existence of complex numbers, quaternions and octonions,
respectively. For definiteness, let us consider
S
3
=
(x
1
, x
2
, x
3
, x
4
)
4
i=1
(x
i
)
2
= 1
embedded in (
4
,δ). Three orthonormal vectors
e
1
(x) = (−x
2
, x
1
, −x
4
, x
3
)
e
2
(x) = (−x
3
, x
4
, x
1
, −x
2
) (7.46)
e
3
(x) = (−x
4
, −x
3
, x
2
, x
1
)
are orthogonal to x = (x
1
, x
2
, x
3
, x
4
) and linearly independent everywhere
on S
3
, hence define the tangent space T
x
S
3
. Two vectors V
1
(x ) and V
2
(y)
are parallel if V
1
(x) =
c
i
e
i
(x) and V
2
( y) =
c
i
e
i
( y). The connection
coefficients are computed from (7.14). Let εe
1
(x) be a small displacement
under which x = (x
1
, x
2
, x
3
, x
4
) changes to x
= x + εe
1
(x) ={x
1
−
εx
2
, x
2
+ εx
1
, x
3
− εx
4
, x
4
+ εx
3
}. The difference between the basis vectors
at x and x
is e
2
(x
) − e
2
(x) = (−x
3
− εx
4
, x
4
+ εx
3
, x
1
− εx
2
, −x
2
− εx
1
) −
(−x
3
, x
4
, x
1
, −x
2
) =−εe
3
(x) = ε
µ
12
e
µ
(x), hence
3
12
=−1,
1
12
=
2
12
= 0. Similarly,
3
21
= 1 hence we find T
3
12
=−2. The reader
should complete the computation of the connection coefficients and verify that
T
λ
µν
=−2 (+2) if (λµν) is an even (odd) permutation of (123) and vanishes
otherwise.
Let us see how this parallelizability of S
3
is related to the existence of
quaternions. The multiplication rule of quaternions is
(x
1
, x
2
, x
3
, x
4
) · (y
1
, y
2
, y
3
, y
4
)
= (x
1
y
1
− x
2
y
2
− x
3
y
3
− x
4
y
4
, x
1
y
2
+ x
2
y
1
+ x
3
y
4
− x
4
y
3
,
x
1
y
3
− x
2
y
4
+ x
3
y
1
+ x
4
y
2
, x
1
y
4
+ x
2
y
3
− x
3
y
2
+ x
4
y
1
). (7.47)
S
3
may be defined by the set of unit quaternions
S
3
={(x
1
, x
2
, x
3
, x
4
)|x ·¯x = 1}
where the conjugate of x is defined by ¯x = (x
1
, −x
2
, −x
3
, −x
4
). According to
(7.46), the tangent space at x
0
= (1, 0, 0, 0) is spanned by
e
1
= (0, 1, 0, 0) e
2
= (0, 0, 1, 0) e
3
= (0, 0, 0, 1).
Then the basis vectors (7.46) of the tangent space at x = (x
1
, x
2
, x
3
, x
4
) are
expressed as the quaternion products
e
1
(x) = e
1
· xe
2
(x) = e
2
· xe
3
(x) = e
3
· x. (7.48)
Because of this algebra, it is always possible to give a set of basis vectors at an
arbitrary point of S
3
once it is given at some point, x
0
= (1, 0, 0, 0), for example.
By the same token, a Lie group is parallelizable. If the set of basis vectors
{V
1
,...,V
m
} at the unit element e of a Lie group G is given, we can always find
a set of basis vectors of T
g
G by the left translation of {V
µ
} (see section 5.6),
{V
1
,...,V
n
}
L
g∗
−→ { X
1
|
g
,...,X
n
|
g
}. (7.49)
7.3.3 The Ricci tensor and the scalar curvature
From the Riemann curvature tensor, we construct new tensors by contracting the
indices. The Ricci tensor Ric is a type (0, 2) tensor defined by
Ric(X, Y ) ≡dx
µ
, R(e
µ
, Y )X (7.50a)

whose component is
Ric
µν
= Ric(e
µ
, e
ν
) = R
λ
µλν
. (7.50b)
The scalar curvature
is obtained by further contracting indices,
≡ g
µν
Ric(e
µ
, e
ν
) = g
µν
Ric
µν
. (7.51)
7.4 Levi-Civita connections
7.4.1 The fundamental theorem
Among affine connections, there is a special connection called the Levi-Civita
connection, which is a natural generalization of the connection in the classical
differential geometry of surfaces. A connection ∇ is called a symmetric
connection if the torsion tensor vanishes. In the coordinate basis, connection
coefficients of a symmetric connection satisfy
λ
µν
=
λ
νµ
. (7.52)
Theorem 7.1. (The fundamental theorem of (pseudo-)Riemannian geometry)
On a (pseudo-)Riemannian manifold (M, g), there exists a unique symmetric
connection which is compatible with the metric g. This connection is called the
Levi-Civita connection.
Proof. This follows directly from (7.34). Let ∇ be an arbitrary connection such
that
(
κ
µν
=
κ
µν
+ K
κ
µν
where
7
κ
µν
8
is the Christoffel symbol and K the contorsion tensor. It was shown
in exercise 7.5 that
κ
µν
≡
(
κ
µν
+ t
κ
µν
is another connection coefficient if t is
a tensor field of type (1, 2). Now we choose t
κ
µν
=−K
κ
µν
so that
κ
µν
=
κ
µν
=
1
2
g
κλ
(∂
µ
g
λν
+ ∂
ν
g
λµ
− ∂
λ
g
µν
). (7.53)
By construction, this is symmetric and certainly unique given a metric.
Exercise 7.8. Let V be a Levi-Civita connection.
(a) Let f ∈
(M). Show that
∇
µ
∇
ν
f =∇
ν
∇
µ
f. (7.54)
(b) Let ω ∈
1
(M). Show that
dω = (∇
µ
ω)
ν
dx
µ
∧ dx
ν
. (7.55)
