Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.

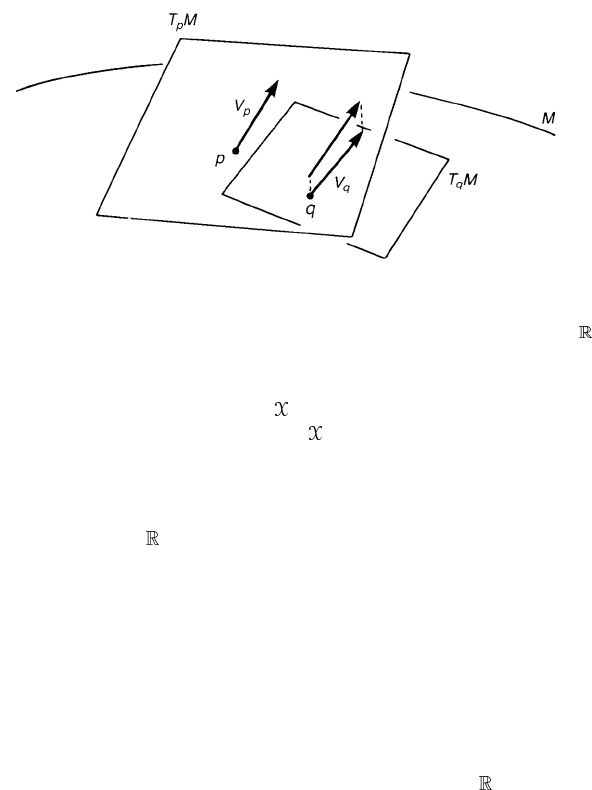
Figure 7.6. On a surface M, a vector V
p
∈ T
p
M is defined to be parallel to V
q
∈ T
q
M if
the projection of V
q
onto T
p
M is parallel to V
p
in our ordinary sense of parallelism in
2
.
(c) Let ω ∈
1
(M) and let U ∈ (M) be the corresponding vector field:
U
µ
= g
µν
ω
ν
. Show that, for any V ∈ (M),
g(∇
X
U, V ) =∇
X
ω, V . (7.56)
Example 7.3.
(a) The metric on
2
in polar coordinates is g = dr ⊗ dr + r
2
dφ ⊗ dφ.
The non-vanishing components of the Levi-Civita connection coefficients
are
φ
rφ
=
φ
φr
= r
−1
and
r
φφ
=−r. This is in agreement with the
result obtained in example 7.1.
(b) The induced metric on S
2
is g = dθ ⊗ dθ + sin
2
θ dφ ⊗ dφ. The non-
vanishing components of the Levi-Civita connection are
θ
φφ
=−cos θ sin θ
φ
θφ
=
φ
φθ
= cot θ. (7.57)
7.4.2 The Levi-Civita connection in the classical geometry of surfaces
In the classical differential geometry of surfaces embedded in
3
, Levi-Civita
defined the parallelism of vectors at the nearby points p and q in the following
sense (figure 7.6). First, take the tangent plane at p and a vector V
p
at p,which
lies in the tangent plane. A vector V
q
at q is defined to be parallel to V
p
if the
projection of V
q
to the tangent plane at p is parallel to V
p
in our usual sense.
Now take two points q and s near p as in figure 7.7 and parallel transport the
displacement vectors pq along ps and ps along pq. If the parallelism is defined
in the sense of Levi-Civita, the displacement vectors projected to the tangent
plane at p form a closed parallelogram, hence this parallelism has vanishing
torsion. As has been proved in theorem 7.1, there exists a unique connection
which has vanishing torsion, which generalizes the parallelism defined here to
arbitrary manifolds.

Figure 7.7. If the parallelism is defined in the sense of Levi-Civita, the torsion vanishes
identically.
7.4.3 Geodesics
When the Levi-Civita connection is employed, we can compute the connection
coefficients, Riemann tensors and many relations involving these by simple
routines. Besides this simplicity, the Levi-Civita connection provides a geodesic
(defined as the straightest possible curve) with another picture, namely the
shortest possible curve connecting two given points. In Newtonian mechanics,
the trajectory of a free particle is the straightest possible as well as the shortest
possible curve, that is, a straight line. Einstein proposed that this property should
be satisfied in general relativity as well; if gravity is understood as a part of the
geometry of spacetime, a freely falling particle should follow the straightest as
well as the shortest possible curve. [Remark: To be precise, the shortest possible
curve is too strong a condition. As we see later, a geodesic defined with respect
to the Levi-Civita connection gives the local extremum of the length of a curve
connecting two points.]
Example 7.4. In a flat manifold (
m
,δ) or (
m
,η), the Levi-Civita connection
coefficients vanish identically. Hence, the geodesic equation (7.19b) is easily
solved to yield x
µ
= A
µ
t + B
µ
,whereA
µ
and B
µ
are constants.
Exercise 7.9. A metric on a cylinder S
1
× is given by g = dφ ⊗ dφ +dz ⊗ dz,
where φ is the polar angle of S
1
and z the coordinate of . Show that the geodesics
given by the Levi-Civita connection are helices.
The equivalence of the straightest possible curve and the local extremum of
the distance is proved as follows. First we parametrize the curve by the distance s
along the curve, x
µ
= x
µ
(s). The length of a path c connecting two points p and
q is
I (c) =
c
ds =
c
0
g
µν
x
µ
x
ν
ds (7.58)
where x
µ
= dx
µ
/ds. Instead of deriving the Euler–Lagrange equation from
(7.58), we will solve a slightly easier problem. Let F ≡
1
2
g
µν
x
µ
x
ν
and write

(7.58) as I (c) =
c
L(F)ds. The Euler–Lagrange equation for the original
problem takes the form
d
ds
∂ L
∂x
λ
−
∂ L
∂x
λ
= 0. (7.59)
Then F = L
2
/2 satisfies
d
ds
∂ F
∂x
λ
−
∂ F
∂x
λ
= L
d
ds
∂ L
∂x
λ
−
∂ L
∂x
λ
+
∂ L
∂x
λ
dL
ds
=
∂ L
∂x
λ
dL
ds
. (7.60)
The last expression vanishes since L ≡ 1 along the curve; dL/ds = 0. Now
we have proved that F also satisfies the Euler–Lagrange equation provided that L
does so. We then have
d
ds
(g
λµ
x
µ
) −
1
2
∂g
µν
∂x
λ
x
µ
x
ν
=
∂g
λµ
∂x
ν
x
µ
x
ν
+ g
λµ
d
2
x
µ
ds
2
−
1
2
∂g
µν
∂x
λ
x
µ
x
ν
= g
λµ
d
2
x
µ
ds
2
+
1
2
∂g
λµ
∂x
ν
+
∂g
λν
∂x
µ
−
∂g
µν
∂x
λ
dx
µ
ds
dx
ν
ds
= 0. (7.61)
If (7.61) is multiplied by g
κλ
, we reproduce the geodesic equation (7.19b).
Having proved that L and F satisfy the same variational problem, we take
advantage of this to compute the Christoffel symbols. Take S
2
, for example. F is
given by
1
2
(θ
2
+ sin
2
θφ
2
) and the Euler–Lagrange equations are
d
2
θ
ds
2
− sin θ cos θ
dφ
ds
2
= 0 (7.62a)
d
2
φ
ds
2
+ 2cotθ
dφ
ds
dθ
ds
= 0. (7.62b)
It is easy to read off the connection coefficients
θ
φφ
=−sin θ cos θ and
φ
φθ
=
φ
θφ
= cot θ , see (7.57).
Example 7.5. Let us compute the geodesics of S
2
. Rather than solving the
geodesic equations (7.62) we find the geodesic by minimizing the length of a
curve connecting two points on S
2
. Without loss of generality, we may assign
coordinates (θ
1
,φ
0
) and (θ
2
,φ
0
) to these points. Let φ = φ(θ) beacurve
connecting these points. Then the length of the curve is
I (c) =
θ
2
θ
1
9
1 +sin
2
dφ
dθ
2
dθ (7.63)

which is minimized when dφ/dθ ≡ 0, that is φ ≡ φ
0
. Thus, the geodesic is a
great circle (θ, φ
0
), θ
1
≤ θ ≤ θ
2
.[Remark: Solving (7.62) is not very difficult.
Let θ = θ(φ) be the equation of the geodesic. Then
dθ
ds
=
dθ
dφ
dφ
ds
d
2
θ
ds
2
=
d
2
θ
dφ
2
dφ
ds
2
+
dθ
dφ
d
2
φ
ds
2
.
Substituting these into the first equation of (7.62), we obtain
d
2
θ
dφ
2
dφ
ds
2
+
dθ
dφ
d
2
φ
ds
2
− sin θ cos θ
dφ
ds
2
= 0. (7.64)
The second equation of (7.62) and (7.64) yields
d
2
θ
dφ
2
− 2cotθ
dθ
dφ
2
− sin θ cos θ = 0. (7.65)
If we define f (θ ) ≡ cot θ , (7.65) becomes
d
2
f
dφ
2
+ f = 0
whose general solution is f (θ ) = cot θ = A cos φ + B sin φ or
A sin θ cos φ + B sin θ sin φ − cos θ = 0. (7.66)
Equation (7.66) is the equation of a great circle which lies in a plane whose normal
vector is (A, B, −1).]
Example 7.6. Let U be the upper half-plane U ≡{(x, y)|y > 0} and introduce
the Poincar
´
e metric
g =
dx ⊗ dx + dy ⊗ dy
y
2
. (7.67)
The geodesic equations are
x
−
2
y
x
y
= 0 (7.68a)
y
−
1
y
[x
2
+ 3y
2
]=0 (7.68b)
where x
≡ dx/ds etc. The first equation of (7.68) is easily integrated, if divided
by x
, to yield
x
y
2
=
1
R
(7.69)
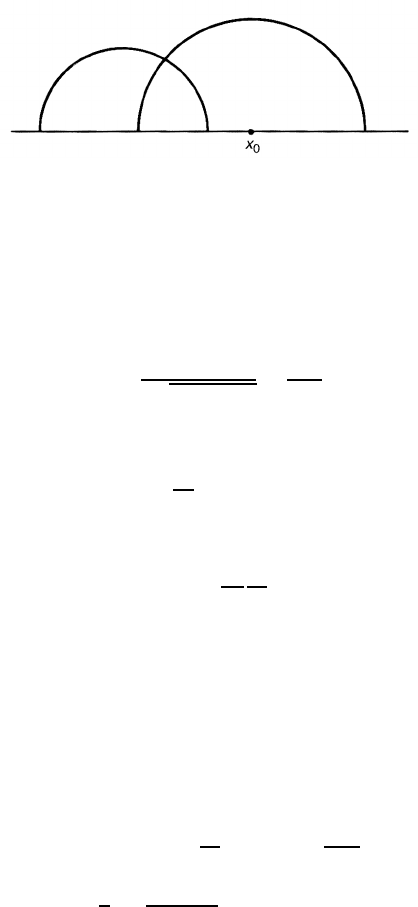
Figure 7.8. Geodesics defined by the Poincar´e metric in the upper half-plane. The geodesic
has an infinite length.
where R is a constant. Since the parameter s is taken so that the vector (x
, y
)
has unit length, it satisfies (x
2
+ y
2
)/y
2
= 1. From (7.69), this becomes
y
2
/R
2
+ (y
/y)
2
= 1or
ds =
dy
y
1 − y
2
/R
2
=
dt
sin t
whereweputy = R sin t. Equation (7.69) then becomes
x
=
y
2
R
= R sin
2
t.
Now x is solved for t to yield
x =
x
ds =
dx
ds
ds
dt
dt
=
R sin t dt =−R cos t + x
0
.
Finally, we obtain the solution
x =−R cos t + x
0
y = R sin t (y > 0) (7.70)
which is a circle with radius R centred at (x
0
, 0). Maximally extended geodesics
are given by 0 < t <π(figure 7.8) whose length is infinite,
I =
ds =
π−ε
0+ε
ds
dt
dt =
π−ε
0+ε
1
sin t
dt
=−
1
2
log
1 +cos t
1 −cos t
π−ε
0+ε
−−−−−−→
ε→0
∞.
7.4.4 The normal coordinate system
The subject here is not restricted to Levi-Civita connections but it does take an
especially simple form when the Levi-Civita connection is employed. Let c(t) be

a geodesic in (M, g) defined with respect to a connection ∇, which satisfies
c(0) = p,
d
dt
p
= X = X
µ
e
µ
∈ T
p
M (7.71)
where {e
µ
} is the coordinate basis at p. Any geodesic emanating from p is
specified by giving X ∈ T
p
M. Take a point q near p. There are many geodesics
which connect p and q. However, there exists a unique geodesic c
q
such that
c
q
(1) = q.LetX
q
∈ T
p
M be the tangent vector of this geodesic at p.As
long as q is not far from p, q uniquely specifies X
q
= X
µ
q
e
µ
∈ T
p
M and
ϕ : q → X
µ
q
serves as a good coordinate system in the neighbourhood of p.
This coordinate system is called the normal coordinate system based on p with
basis {e
µ
}. Obviously ϕ(p) = 0. We define a map EXP : T
p
M → M by
EXP : X
q
→ q. By definition, we have
ϕ(EXP X
µ
q
e
µ
) = X
µ
q
. (7.72)
With respect to this coordinate system, a geodesic c(t) with c(0) = p and
c(1) = q has the coordinate presentation
ϕ(c(t)) = X
µ
= X
µ
q
t (7.73)
where X
µ
q
are the normal coordinates of q.
We now show that Levi-Civita connection coefficients vanish in the normal
coordinate system. We write down the geodesic equation in the normal coordinate
system,
0 =
d
2
X
µ
dt
2
+
µ
νλ
(X
κ
q
t)
dX
ν
dt
dX
λ
dt
=
µ
νλ
(X
κ
q
t)X
ν
q
X
λ
q
. (7.74)
Since
µ
νλ
( p)X
ν
q
X
λ
q
= 0forany X
ν
q
at p for which t = 0, we find
µ
νλ
( p) +
µ
λν
( p) = 0. Since our connection is symmetric we must have
µ
νλ
( p) = 0. (7.75)
As a consequence, the covariant derivative of any tensor t in this coordinate
system takes the extremely simple form at p,
∇
X
t
...
...
= X [t
...
...
]. (7.76)
Equation (7.75) does not imply that
µ
νλ
vanishes at q (=p). In fact, we
find from (7.42) that
R
κ
λµν
( p) = ∂
µ
κ
νλ
( p) − ∂
ν
κ
µλ
( p) (7.77)
hence ∂
µ
κ
νλ
( p) = 0ifR
κ
λµν
( p) = 0.

7.4.5 Riemann curvature tensor with Levi-Civita connection
Let ∇ be the Levi-Civita connection. The components of the Riemann curvature
tensor are given by (7.42) with
λ
µν
=
κ
µν
while the torsion tensor vanishes by definition. Many formulae are simplified if
the Levi-Civita connections are employed.
Exercise 7.10.
(a) Let g = dr ⊗dr +r
2
(dθ ⊗dθ +sin
2
θ dφ ⊗dφ) bethemetricof(
3
,δ),
where 0 ≤ θ ≤ π,0≤ φ<2π. Show, by direct calculation, that all the
components of the Riemann curvature tensor with respect to the Levi-Civita
connection vanish.
(b) The spatially homogeneous and isotropic universe is described by the
Robertson–Walker metric,
g =−dt ⊗dt +a
2
(t)
dr ⊗ dr
1 − kr
2
+r
2
(dθ ⊗ dθ + sin
2
θ dφ ⊗ dφ)
(7.78)
where k is a constant, which may be chosen to be −1, 0or+1byasuitable
rescaling of r and 0 ≤ θ ≤ π,0≤ φ<2π.Ifk =+1, r is restricted to
0 ≤ r < 1. Compute the Riemann tensor, the Ricci tensor and the scalar
curvature.
(c) The Schwarzschild metric takes the from
g =−
1 −
2M
r
dt ⊗ dt
+
1
1 −
2M
r
dr ⊗ dr +r
2
(dθ ⊗ dθ + sin
2
θ dφ ⊗ dφ) (7.79)
where 0 < 2M < r,0≤ θ ≤ π,0≤ φ<2π. Compute the Riemann
tensor, the Ricci tensor and the scalar curvature. [Remark: The metric (7.79)
describes a spacetime of a spherically symmetric object with mass M.]
Exercise 7.11. Let R be the Riemann tensor defined with respect to the Levi-
Civita connection. Show that
R
κλµν
=
1
2
∂
2
g
κµ
∂x
λ
∂x
ν
−
∂
2
g
λµ
∂x
κ
∂x
ν
−
∂
2
g
κν
∂x
λ
∂x
µ
+
∂
2
g
µν
∂x
κ
∂x
µ
+ g
ζη
(
ζ
κµ
η
λν
−
ζ
κν
η
λµ
)

where R
κλµν
≡ g
κζ
R
ζ
λµν
. Verify the following symmetries,
R
κλµν
=−R
κλνµ
(cf (7.43)) (7.80a)
R
κλµν
=−R
λκµν
(7.80b)
R
κλµν
= R
µνκλ
(7.80c)
Ric
µν
= Ric
νµ
. (7.80d)
Theorem 7.2. (Bianchi identities)LetR be the Riemann tensor defined with
respect to the Levi-Civita connection. Then R satisfies the following identities:
R(X, Y )Z + R(Z , X )Y + R(Y, Z )X = 0
(the first Bianchi identity) (7.81a)
(∇
X
R)(Y, Z )V + (∇
Z
R)(X, Y )V +(∇
Y
R)(Z , X)V = 0
(the second Bianchi identity). (7.81b)
Proof. Our proof follows Nomizu (1981). Define the symmetrizor
by
{ f (X, Y, Z )}=f (X, Y, Z ) + f (Z , X, Y ) + f (Y, Z , X ). Let us prove the
first Bianchi identity
{R(X, Y )Z }=0. Covariant differentiation of the identity
T (X, Y ) =∇
X
Y −∇
Y
X −[X, Y ]=0 with respect to Z yields
0 =∇
Z
{∇
X
Y −∇
Y
X −[X, Y ]}
=∇
Z
∇
X
Y −∇
Z
∇
Y
X −{∇
[X,Y ]
Z +[Z , [X, Y ]]}
where the torsion-free condition has been used again to derive the second equality.
Symmetrizing this, we have
0 =
{∇
Z
∇
X
Y −∇
Z
∇
Y
X −∇
[X,Y ]
Z −[Z , [X, Y ]]}
=
{∇
Z
∇
X
Y −∇
Z
∇
Y
X −∇
[X,Y ]
Z}= {R(X, Y )Z}
where the Jacobi identity
{[X, [Y, Z ]]} = 0 has been used.
The second Bianchi identity becomes
{(∇
X
R)(Y, Z )}V = 0where
symmetrizes (X, Y, Z) only. If the identity R(T (X, Y ), Z )V = R(∇
X
Y −∇
Y
X −
[X, Y ], Z)V = 0 is symmetrized, we have
0 =
{R(∇
X
Y, Z ) − R(∇
Y
X, Z ) − R([X, Y ], Z )}V
=
{R(∇
Z
X, Y ) − R(X, ∇
Z
Y ) − R([X, Y ], Z)}V . (7.82)
If we note the Leibnitz rule,
∇
Z
{R(X, Y )V }=(∇
Z
R)(X, Y )V
+ R(X, Y )∇
Z
V + R(∇
Z
X, Y )V + R(X, ∇
Z
Y )V
(7.82) becomes
0 =
{−(∇
Z
R)(X, Y ) +[∇
Z
, R(X, Y )]−R([X, Y ], Z )}V .

The last two terms vanish if R(X, Y )V ={[∇
X
, ∇
Y
]−∇
[X,Y ]
}V is substituted
into them,
{[∇
Z
, R(X, Y )]−R([X, Y ], Z )}V
=
{[∇
Z
, [∇
X
, ∇
Y
]] − [∇
Z
, ∇
[X,Y ]
]−[∇
[X,Y ]
, ∇
Z
]+∇
[[X,Y ],Z ]
}V
= 0
where the Jacobi identities
{[∇
Z
, [∇
X
, ∇
Y
]]} = {[[X, Y ], Z ]} = 0 have been
used. We finally obtain
{(∇
X
R)(Y, Z )}V = 0.
In components, the Bianchi identities are
R
κ
λµν
+ R
κ
µνλ
+ R
κ
νλµ
= 0
(the first Bianchi identity) (7.83a)
(∇
κ
R)
ξ
λµν
+ (∇
µ
R)
ξ
λνκ
+ (∇
ν
R)
ξ
λκµ
= 0
(the second Bianchi identity). (7.83b)
By contracting the indices ξ and µ of the second Bianchi identity, we obtain an
important relation:
(∇
κ
Ric)
λν
+ (∇
µ
R)
µ
λνκ
− (∇
ν
Ric)
λκ
= 0. (7.84)
If the indices λ and ν are further contracted, we have ∇
µ
( δ − 2Ric)
µ
κ
= 0or
∇
µ
G
µν
= 0 (7.85)
where G
µν
is the Einstein tensor defined by
G
µν
= Ric
µν
−
1
2
g
µν
. (7.86)
Historically, when Einstein formulated general relativity, he first equated the Ricci
tensor Ric
µν
to the energy–momentum tensor T
µν
. Later he realized that T
µν
satisfies the covariant conservation equation ∇
µ
T
µν
= 0 while Ric
µν
does not.
To avoid this difficulty, he proposed that G
µν
should be equated to T
µν
.This
new equation is natural in the sense that it can be derived from a scalar action by
variation, see section 7.10.
Exercise 7.12. Let (M, g) be a two-dimensional manifold with g =−dt ⊗ dt +
R
2
(t)dx ⊗ dx ,whereR(t) is an arbitrary function of t. Show that the Einstein
tensor vanishes.
The symmetry properties (7.80a)–(7.80c) restrict the number of independent
components of the Riemann tensor. Let m be the dimension of a manifold (M, g).
The anti-symmetry R
κλµν
=−R
λκνµ
implies that there are N ≡
m
2
independent
choices of the pair (µ, ν). Similarly, from R
κλµν
=−R
λκµν
,wefindthereare
N independent pairs of (κ, λ).SinceR
κλµν
is symmetric with respect to the
interchange of the pairs (κ, λ) and (µ, ν), the number of independent choices of
the pairs reduces from N
2
to
N+1
2
=
1
2
N(N + 1). The first Bianchi identity
R
κλµν
+ R
κµνλ
+ R
κνλµ
= 0 (7.87)
further reduces the number of independent components. The LHS of (7.87) is
totally anti-symmetric with respect to the interchange of the indices (λ,µ,ν).
Furthermore, the anti-symmetry (7.80b) ensures that it is totally anti-symmetric
in all the indices. If m < 4, (7.87) is trivially satisfied and it imposes no additional
restrictions. If m ≥ 4, (7.87) yields non-trivial constraints only when all the
indices are different. The number of constraints is equal to the number of possible
ways of choosing four different indices out of m indices, namely
m
4
. Noting
that
m
4
= m(m − 1)(m − 2)(m − 3)/4! vanishes for m < 4, the number of
independent components of the Riemann tensor is given by
F(m) =
1
2
m
2
m
2
+ 1
−
m
4
=
1
12
m
2
(m
2
− 1). (7.88)
F(1) = 0 implies that one-dimensional manifolds are flat. Since F(2) = 1, there
is only one independent component R
1212
on a two-dimensional manifold, other
components being either 0 or ±R
1212
. F(4) = 20 is a well-known fact in general
relativity.
Exercise 7.13. Let (M, g) be a two-dimensional manifold. Show that the
Riemann tensor is written as
R
κλµν
= K (g
κµ
g
λν
− g
κν
g
λµ
) (7.89)
where K ∈
(M). Compute the Ricci tensor to show Ric
µν
∝ g
µν
. Compute the
scalar curvature to show K =
/2.
7.5 Holonomy
Let (M, g) be an m-dimensional Riemannian manifold with an affine connection
∇. The connection naturally defines a transformation group at each tangent space
T
p
M as follows.
Definition 7.3. Let p be a point in (M, g) and consider the set of closed loops at
p, {c(t)|0 ≤ t ≤ 1, c(0) = c(1) = p}. Take a vector X ∈ T
p
M and parallel
transport X along a curve c(t). After a trip along c(t), we end up with a new
vector X
c
∈ T
p
M. Thus, the loop c(t) and the connection ∇ induce a linear
transformation
P
c
: T
p
M → T
p
M. (7.90)
The set of these transformations is denoted by H ( p) and is called the holonomy
group at p.
