Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

9.4.3 Triviality of bundles

A ﬁbre bundle is trivial if it is expressed as a direct product of the base space and

the ﬁbre. The following theorem gives the condition under which a ﬁbre bundle

is trivial.

Theorem 9.2. A principal bundle is trivial if and only if it admits a global section.

Proof.Let(P,π,M, G) be a principal bundle over M and let s ∈ (M, P)

be a global section. This section may be used to show that there exists a

homeomorphism between P and M × G.Ifa is an element of G, the product

s( p)a belongs to the ﬁbre at p. Since the right action is transitive and free, any

element u ∈ P is uniquely written as s( p)a for some p ∈ M and a ∈ G.Deﬁne

amap : P → M × G by

 : s( p)a → ( p, a). (9.73)

It is easily veriﬁed that  is indeed a homeomorphism and we have shown that P

is a trivial bundle M × G.

Conversely, suppose P

∼

M × G.Letφ : M × G → P be a trivialization.

Take a ﬁxed element g ∈ G.Thens

: M → P deﬁned by s

( p) = φ(p, g) is a

global section.

Is there a corresponding theorem for vector bundles? We know that any

vector bundle admits a global null section. Thus, we cannot simply replace P by

E in theorem 9.2. Let us consider the associated principal bundle P(E) of E.

By deﬁnition, E and P(E) share the same set of transition functions. Since the

twisting of a bundle is described purely by the transition functions, we obtain the

following corollary.

Corollary 9.2. A vector bundle E is trivial if and only if its associated principal

bundle P(E) admits a global section.

Problems

9.1 Let L be the real line bundle over S

(i.e. L is either the cylinder S

× or

the M¨obius strip). Show that the Whitney sum L ⊕ L is a trivial bundle. Sketch

L ⊕ L to conﬁrm the result.

9.2 Let 

be the volume element of S

normalized as





= 1. Let

f : S

2n−1

→ S

be a smooth map and consider the pullback f

∗



(a) Show that f

∗



is closed and written as dω

n−1

,whereω

n−1

is an (n − 1)-

form on S

2n−1

(b) Show that the Hopf invariant

H ( f ) ≡



2n−1

n−1

∧ dω

n−1

is independent of the choice of ω

n−1

(d) Show that H ( f ) = 0ifn is odd. [Hint:Useω

n−1

∧ dω

n−1

d(ω

n−1

∧

n−1

).]

(e) Compute the Hopf invariant of the map π : S

→ S

deﬁned in example 9.9.

CONNECTIONS ON FIBRE BUNDLES

In chapter 7 we introduced connections in Riemannian manifolds which enable us

to compare vectors in different tangent spaces. In the present chapter connections

on ﬁbre bundles are deﬁned in an abstract though geometrical way.

We ﬁrst deﬁne a connection on a principal bundle. Our abstract deﬁnition

is realized concretely by introducing the connection one-form whose local form

is well known to physicists as a gauge potential. The Yang–Mills ﬁeld strength

is deﬁned as the curvature associated with the connection. A connection on a

principal bundle naturally deﬁnes a covariant derivative in the associated vector

bundle. We reproduce the results obtained in chapter 7, applying our approach to

tangent bundles. We conclude this chapter with a few applications of connections

to physics: to gauge ﬁeld theories and Berry’s phase. We follow the line of

Choquet-Bruhat et al (1982), Kobayashi (1984) and Nomizu (1981). Details will

be found in the classic books by Kobayashi and Nomizu (1963, 1969). See also

Daniel and Viallet (1980) for a quick review.

10.1 Connections on principal bundles

There are several equivalent deﬁnitions of a connection on a principal bundle.

Our approach is based on the separation of tangent space T

P into ‘vertical’

and ‘horizontal’ subspaces. Although this approach seems to be abstract, it is

advantageous compared with other approaches in that it clariﬁes the geometrical

pictures involved and is deﬁned independently of special local trivializations.

Connections are also deﬁned as

-valued one-forms which satisfy certain axioms.

These deﬁnitions are shown to be equivalent.

We brieﬂy summarize the basic facts on Lie groups and Lie algebras, since

we shall make extensive use of these (see section 5.6 for details). Let G be a

Lie group. The left action L

and the right action R

are deﬁned by L

h = gh

and R

h = hg for g, h ∈ G. L

induces a map L

g∗

: T

(G) → T

(G).A

left-invariant vector ﬁeld X satisﬁes L

g∗

= X |

. Left-invariant vector ﬁelds

form a Lie algebra of G, denoted by

.SinceX ∈ is speciﬁed by its value at the

unit element e,andvice versa, there exists a vector space isomorphism

∼

The Lie algebra

is closed under the Lie bracket, [T

, T

]= f

αβ

where {T

}

is the set of generators of

. f

αβ

are called the structure constants. The adjoint

action ad : G → G is deﬁned by ad

h ≡ ghg

−1

. The tangent map of ad

called the adjoint map and is denoted by Ad

: T

(G) → T

ghg

−1

(G). If restricted

to T

(G)  ,Ad

maps onto itself; Ad

: → as A → gAg

−1

, A ∈ .

10.1.1 Deﬁnitions

Let u be an element of a principal bundle P(M, G) and let G

be the ﬁbre at

p = π(u).Thevertical subspace V

P is a subspace of T

P which is tangent to

at u.[Wa rn i ng : T

P is the tangent space of P and should not be confused

with the tangent space T

M of M.] Let us see how V

P is constructed. Take an

element A of

. By the right action

exp(tA)

u = u exp(tA)

a curve through u is deﬁned in P.Sinceπ(u) = π(u exp(tA)) = p, this curve

lies within G

. Deﬁne a vector A

∈ T

P by

f (u) =

f (u exp(tA))|

t=0

(10.1)

where f : P →

is an arbitrary smooth function. The vector A

is tangent to

P at u, hence A

∈ V

P. In this way we deﬁne a vector A

at each point of P

and construct a vector ﬁeld A

, called the fundamental vector ﬁeld generated

by A. There is a vector space isomorphism  :

→ V

P given by A → A

The horizontal subspace H

P is a complement of V

P in T

P and is uniquely

speciﬁed if a connection is deﬁned in P.

Exercise 10.1.

(a) Show that π

∗

X = 0forX ∈ V

(b) Show that  preserves the Lie algebra structure:

, B

]=[A, B]

. (10.2)

Deﬁnition 10.1. Let P(M, G) be a principal bundle. A connection on P is a

unique separation of the tangent space T

P into the vertical subspace V

P and

the horizontal subspace H

P such that

(i) T

P = H

P ⊕ V

(ii) A smooth vector ﬁeld X on P is separated into smooth vector ﬁelds

∈ H

P and X

∈ V

P as X = X

+ X

(iii) H

P = R

g∗

P for arbitrary u ∈ P and g ∈ G; see ﬁgure 10.1.

The condition (iii) states that horizontal subspaces H

P and H

P on

the same ﬁbre are related by a linear map R

g∗

induced by the right action.

Accordingly, a subspace H

P at u generates all the horizontal subspaces on the

same ﬁbre. This condition ensures that if a point u is parallel transported, so is its

constant multiple ug, g ∈ G; see later. At this point, the reader might feel rather

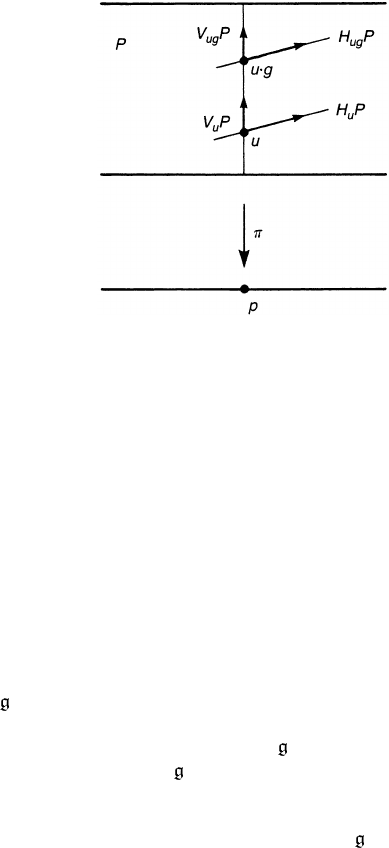
Figure 10.1. The horizontal subspace H

P is obtained from H

P by the right action.

uneasy about our deﬁnition of a connection. At ﬁrst sight, this deﬁnition seems

to have nothing to do with the gauge potential or the ﬁeld strength. We clarify

these points after we introduce the connection one-form on P. We again stress

that our deﬁnition, which is based on the separation T

P = V

P ⊕H

P, is purely

geometrical and is deﬁned independently of any extra information. Although the

connection becomes more tractable in the following, the geometrical picture and

its intrinsic nature are generally obscured.

10.1.2 The connection one-form

In practical computations, we need to separate T

P into V

P and H

P in a

systematic way. This can be achieved by introducing a Lie-algebra-valued one-

form ω ∈

⊗ T

∗

P called the connection one-form.

Deﬁnition 10.2. A connection one-form ω ∈

⊗T

∗

P is a projection of T

P onto

the vertical component V

P  . The projection property is summarized by the

following requirements,

(i) ω(A

) = AA∈ (10.3a)

(ii) R

∗

ω = Ad

−1

ω (10.3b)

that is, for X ∈ T

∗

(X ) = ω

g∗

X) = g

−1

(X )g.(10.3b



)

Deﬁne the horizontal subspace H

P by the kernel of ω,

P ≡{X ∈ T

P|ω(X ) = 0}. (10.4)

To show that this deﬁnition is consistent with deﬁnition 10.1, we prove the

following proposition.

Proposition 10.1. The horizontal subspaces (10.4) satisfy

g∗

P = H

P. (10.5)

Proof. Fix a point u ∈ P and deﬁne H

P by (10.4). Take X ∈ H

P and construct

g∗

X ∈ T

P.Weﬁnd

ω(R

∗

X) = R

∗

ω(X) = g

−1

ω(X)g = 0

since ω(X) = 0. Accordingly, R

g∗

X ∈ H

P. We note that R

g∗

is an invertible

linear map. Hence, any vector Y ∈ H

P is expressed as Y = R

g∗

X for some

X ∈ H

P. This proves (10.5).

We have shown that the deﬁnition of the connection one-form ω is equivalent

to that of the connection, since ω separates T

P into H

P ⊕V

P in harmony with

the axioms of deﬁnition 10.1. The connection one-form ω deﬁned here is known

as the Ehresmann connection in the literature.

10.1.3 The local connection form and gauge potential

Let {U

} be an open covering of M and let σ

be a local section deﬁned on each

. It is convenient to introduce a Lie-algebra-valued one-form

on U

,by

≡ σ

∗

ω ∈ ⊗ 

). (10.6)

Conversely, given a Lie-algebra-valued one-form

,onU

, we can reconstruct a

connection one-form ω whose pullback by σ

∗

Theorem 10.1. Given a

-valued one-form

on U

and a local section σ

: U

→

−1

), there exists a connection one-form ω such that

= σ

∗

ω.

Proof. Let us deﬁne a

-valued one-form ω on P by

≡ g

−1

∗

+ g

−1

(10.7)

where d

is the exterior derivative on P and g

is the canonical local

trivialization deﬁned by φ

−1

(u) = ( p, g

) for u = σ

( p)g

.Weﬁrstshow

that σ

∗

.ForX ∈ T

M,wehave

∗

(X ) = ω

(σ

i∗

X) = π

∗

(σ

i∗

X) + d

(σ

i∗

(π

∗

i∗

X) + d

(σ

i∗

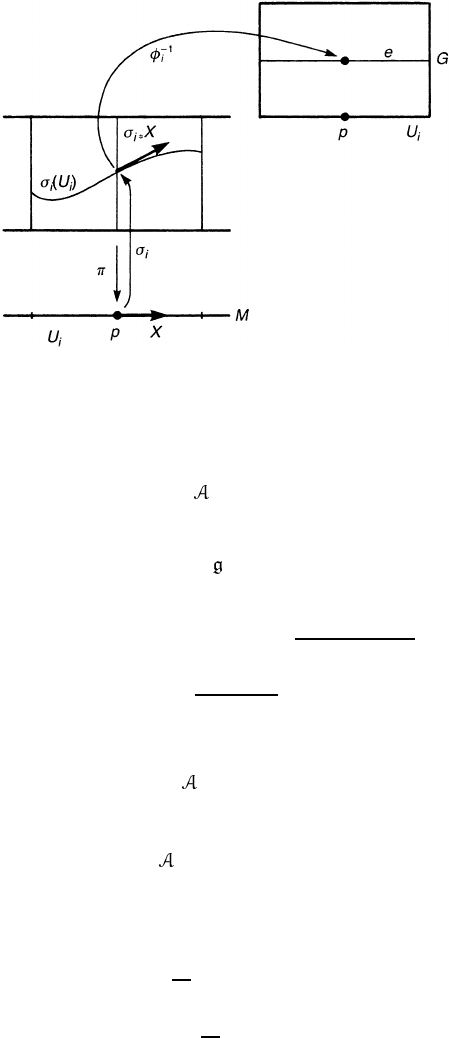
Figure 10.2. The canonical local trivialization deﬁned by the local section σ

over U

where we have noted that σ

i∗

X ∈ T

P and g

= e at σ

, see ﬁgure 10.2. We

further note that π

∗

i∗

= id

(M)

and d

(σ

i∗

X) = 0sinceg ≡ e along σ

i∗

Thus, we have obtained σ

∗

(X ) =

(X ).

Next we show that ω

satisﬁes the axioms of a connection one-form given in

deﬁnition 10.2.

(i) Let X = A

∈ V

P, A ∈ . It follows from exercise 10.1(a) that

∗

X = 0. Now we have

) = g

−1

) = g

(u)

−1

dg (u exp(tA))



t=0

= g

(u)

−1

(u)

dexp(tA)



t=0

= A.

(ii) Take X ∈ T

P and h ∈ G.Wehave

∗

(X ) = ω

h∗

X) = g

−1

iuh

(π

∗

h∗

X)g

iuh

+ g

−1

iuh

h∗

X).

Since g

iuh

= g

h and π

∗

h∗

X = π

∗

X (note that π R

= π), we have

∗

(X ) = h

−1

(π

∗

X)g

h + h

−1

(X )h

= h

−1

(X )h

where we have noted that

−1

iuh

h∗

X) = g

−1

iuh

iγ(t)h



t=0

= h

−1

iγ(t)



t=0

h = h

−1

(X )h.

Here γ(t) is a curve through u = γ(0), whose tangent vector at u is X.

Hence, the

-valued one-form ω

deﬁned by (10.7) indeed satisﬁes

∗

and the axioms of a connection one-form.

For ω to be deﬁned uniquely on P, i.e. for the separation T

P = H

P ⊕V

to be unique, we must have ω

= ω

on U

∩ U

. A unique one-form ω is then

deﬁned throughout P by ω|

= ω

. To fulﬁl this condition, the local forms

have to satisfy a peculiar transformation property similar to that of the Christoffel

symbols. We ﬁrst prove a technical lemma.

Lemma 10.1. Let P(M, G) be a principal bundle and σ

(σ

) be a local section

over U

) such that U

∩ U

=∅.ForX ∈ T

M (p ∈ U

∩ U

), σ

i∗

X and

j ∗

X satisfy

j ∗

X = R

∗

(σ

i∗

X) + (t

−1

(X ))

(10.8)

where t

: U

∩U

→ G is the transition function.

Proof. Take a curve γ :[0, 1]→M such that γ(0) = p and ˙γ(0) = X.Since

( p) and σ

( p) are related by the transition function as σ

( p) = σ

( p)t

( p)

(see (9.43)), we have

j ∗

X =

(γ (t))



t=0

{σ

(t)t

(t)}



t=0

(t) · t

( p) + σ

( p) ·

(t)



t=0

= R

∗

(σ

i∗

X) + σ

( p)t

( p)

−1

(t)



t=0

where σ

(t) stands for σ

(γ (t)) andwehaveassumedthatG is a matrix group for

which R

g∗

X = Xg. We note that

( p)

−1

(X ) = t

( p)

−1

(t)



t=0

( p)

−1

(t)]



t=0

∈ T

(G)

∼

[Note that t

( p)

−1

(γ (t)) = e at t = 0.] This shows that the second term of

j ∗

X represents the vector ﬁeld (t

−1

(X ))

at σ

( p).

The compatibility condition is easily obtained by applying the connection

one-form ω on (10.8). We ﬁnd that

∗

ω(X) = R

∗

ω(σ

i∗

X) + t

−1

(X )

= t

−1

ω(σ

i∗

X)t

+ t

−1

(X )

where the axioms of deﬁnition 10.2 have been used. Since this is true for any

X ∈ T

M, this equation reduces to

= t

−1

+ t

−1

. (10.9)

This is the compatibility condition we have been seeking.

Conversely, given an open covering {U

}, the local sections {σ

} and the

local forms {

} which satisfy (10.9), we may construct the -valued one-form ω

over P. Since a non-trivial principal bundle does not admit a global section, the

pullback

= σ

∗

ω exists locally but not necessarily globally. In gauge theories,

is identiﬁed with the gauge potential (Yang–Mills potential). As we have

seen in the monopole case, the monopole ﬁeld B = gr/r

does not admit a

single gauge potential and we require at least two

to describe this U(1) bundle

over S

Exercise 10.2. Let P(M, G) be a principal bundle over M and let U be a chart of

M. Take local sections σ

and σ

over U such that σ

( p) = σ

( p)g( p).Show

that the corresponding local forms

and

are related as

−1

g + g

−1

dg. (10.10a)

In components, this becomes

2µ

= g

−1

( p)

1µ

( p)g( p) + g

−1

( p)∂

g( p)(10.10b)

which is simply the gauge transformation deﬁned in section 1.8.

Example 10.1. Let P beaU(1) bundle over M. Take overlapping charts U

and

.Let

(

) be a local connection form on U

). The transition function

: U

∩U

→ U(1) is given by

( p) = exp[i( p)] ( p) ∈ . (10.11)

and

are related as

( p) =t

( p)

−1

( p)t

( p) + t

( p)

−1

( p)

( p) + id( p). (10.12a)

In components, we have the familiar expression

j µ

iµ

+ i∂

. (10.12b)

Our connection

differs from the standard vector potential A

by the Lie

algebra factor:

= iA

Here we note again that ω is deﬁned globally over the bundle P(M, G).

Although there are many connection one-forms on P(M, G), they share the same

global information about the bundle. In contrast, an individual local piece (gauge

potential)

is associated with the trivial bundle π

−1

) and cannot have any

global information on P.Itisω or, equivalently, the total of {

} satisfying

the compatibility condition (10.9), which carries the global information about the

bundle.

10.1.4 Horizontal lift and parallel transport

Parallel transport of a vector has been deﬁned in chapter 7 as transport without

change. Parallel transport of an element of a principal bundle along a curve in M

is provided by the ‘horizontal lift’ of the curve.

Deﬁnition 10.3. Let P(M, G) be a G bundle and let γ :[0, 1]→M be a curve

in M.Acurve˜γ :[0, 1]→P is said to be a horizontal lift of γ if π ◦˜γ = γ

and the tangent vector to ˜γ(t) always belongs to H

˜γ(t)

Let

X be a tangent vector to ˜γ . Then it satisﬁes ω(

X ) = 0 by deﬁnition.

This condition is an ordinary differential equation (ODE) and the fundamental

theorem of ODEs guarantees the local existence and uniqueness of the horizontal

lift.

Theorem 10.2. Let γ :[0, 1]→M beacurveinM and let u

∈ π

−1

(γ (0)).

Then there exists a unique horizontal lift ˜γ(t) in P such that ˜γ(0) = u

Let us construct such a curve ˜γ .LetU

be a chart which contains γ and

take a section σ

over U

. If there exists a horizontal lift ˜γ , it may be expressed

as ˜γ(t) = σ

(γ (t))g

(t),whereg

(t) stands for g

(γ (t)) ∈ G. Without loss of

generality, we may take a section such that σ

(γ (0)) =˜γ(0),thatisg

(0) = e.

Let X be a tangent vector to γ(t) at γ(0).Then

X =˜γ

∗

X is tangent to ˜γ at

=˜γ(0). Since the tangent vector

X is horizontal, it satisﬁes ω(

X ) = 0. A

slight modiﬁcation of lemma 10.1 yields

X = g

(t)

−1

i∗

(t) +[g

(t)

−1

(X )]

By applying ω on this equation, we ﬁnd

0 = ω(

X ) = g

(t)

−1

ω(σ

i∗

X)g

(t) + g

(t)

−1

(t)

Multiplying on the left by g

(t),wehave

(t)

=−ω(σ

i∗

X)g

(t). (10.13a)

The fundamental theorem of ODEs guarantees the existence and uniqueness of

the solution of (10.13a).

Since ω(σ

i∗

X) = σ

∗

ω(X) =

(X ), (10.13a) is expressed in a local form

(t)

=−

(X )g

(t)(10.13b)

whose formal solution with g

(0) = e is

(γ (t)) = exp



−



iµ



exp



−



γ(t )

γ(0)

iµ

(γ (t)) dx



(10.14)