Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

4.9 Principal Structures of LM-matrices 251

where A is assumed to be an m × n LM-matrix of rank n. A basic solution

to the dual problem (D) corresponds to an n × n nonsingular submatrix

A[I,C] for some I ⊆ R, and is computed by solving y[I]

A[I,C]=c[I]

and putting y[R \ I]=0. In this case we may be interested in the family

of the decompositions obtained by the CCF of the submatrices A[I,C]for

all I ⊆ R such that A[I,C] is nonsingular. This question is not the same as

the previous one, since the transpose of an LM-matrix is not an LM-matrix.

We shall give a combinatorial answer to this second question by the vertical

principal structure of LM-matrices in §4.9.4.

We may ask a more general question: For an LM-matrix A of rank r, what

is the coarsest decomposition of the row and the column sides which is ﬁner

than any decomposition induced by the CCF of r×r nonsingular submatrices

of A? We address this problem in Remark 4.9.20.

Example 4.9.1. The idea of the vertical principal structure is illustrated

here in an informal manner. Consider a 5 × 3 LM-matrix

A =

12 1

11−1

0 t

with ground ﬁeld Q, where C = {x

}, R = {r

},and

(i =1, ···, 6) are indeterminates. This matrix is LM-irreducible, the whole

matrix being a vertical tail.

For a nonsingular submatrix A[I,C] we denote by P

CCF

(I,C) the par-

tition of C (together with the partial order) in the CCF of the subma-

trix A[I,C]. For I = {r

}, for instance, the CCF of A[I,C]=

A[{r

},C] is given by

1 21

−1 −2

which is obtained from A[{r

},C] by subtracting row r

from row r

Hence, P

CCF

({r

},C) is given by {x

}≺{x

By inspection we see that A[I,C] is a nonsingular submatrix for any I ⊆ R

with |I| =3,andP

CCF

(I,C) for all I are given as follows:

CCF

(I,C) I

}≺{x

}{r

}

}{r

}(i =1, 2; j =3, 4)

}≺{x

} otherwise

252 4. Theory and Application of Mixed Matrices

This shows that the decomposition of C deﬁned by {x

}≺{x

}, {x

}≺

} gives the coarsest common reﬁnement of P

CCF

(I,C) for all I,whichwe

denote by

CCF

(I,C) (see Theorem 2.2.10 for this notation). The vertical

principal structure of A will give a succinct description of

CCF

(I,C)in

Example 4.9.5. 2

4.9.2 Principal Structure of Submodular Systems

The concept of the principal structure of submodular systems was introduced

ﬁrst by Fujishige [81], and subsequently generalized for submodular functions

on arbitrary lattices by Tomizawa–Fujishige [315]. This section is devoted to

a description of this concept.

Let L be a lattice with ﬁnite length and f a submodular function on it:

f(X)+f(Y ) ≥ f(X ∨ Y )+f(X ∧ Y ),X,Y∈L,

where ∨ and ∧ are the join and the meet in L. The partial order  in L is

deﬁned by:

X  Y ⇐⇒ X ∨ Y = Y ( ⇐⇒ X ∧Y = X).

For each X ∈L,

min

(f; X)={Y ∈L|X  Y, f(Y ) = min{f (Y



) | X  Y



∈L}}

(4.134)

forms a sublattice of L by the submodularity of f (the proof is similar to

that of Theorem 2.2.5). We denote by D(f; X) the minimum element of this

sublattice, i.e.,

D(f; X) = min L

min

(f; X). (4.135)

A mapping φ : L→Lis said to be a closure function if it satisﬁes the

following three conditions:

(CL0) ∀X ∈L: X  φ(X),

(CL1) ∀X, Y ∈L: X  Y ⇒ φ(X)  φ(Y ),

(CL2) ∀X ∈L: φ(φ(X)) = φ(X).

With this terminology we have the following lemma.

Lemma 4.9.2. The mapping D(f; · ):L→Lis a closure function on L.

Proof. The conditions (CL0) and (CL2) are immediate from the deﬁnition.

The condition (CL1) is proved as follows. Because of the deﬁnition of D(f; · ),

we have

f(D(f ; Y )) ≤ f(D(f; X) ∨ D

(f; Y )).

It follows from the submodularity of f and the above inequality that

f(D(f ; X)) ≥ f(D(f; X) ∧ D(f; Y )).

4.9 Principal Structures of LM-matrices 253

On the other hand, if X  Y ,itholdsthatX  D(f; X) ∧ D(f; Y ). Hence,

from the minimality of D(f; X)wehaveD(f; X)=D(f; X)∧D(f; Y ), which

implies D(f; X)  D(f; Y ).

For a closure function φ, it can be easily shown that φ(X ∧Y )=X ∧Y if

φ(X)=X and φ(Y )=Y . That is to say, the family {X ∈L|φ(X)=X} of

“closed sets” is a lower semilattice. Therefore the subset K

(f) deﬁned by

(f)={X ∈L|D(f; X)=X} (4.136)

is a lower semilattice containing the maximum element of L. We say that

(f)istheprincipal structure of (L,f). Denoting the minimum sublattice

which contains K

(f)byL

(f), we will call L

(f)theprincipal sublattice

of (L,f).

The principal structure K

(f), which is derived from (4.134), is closely

related to the family of the (global) minimizers of f:

min

(f)={Y ∈L|f(Y ) = min{f(Y



) | Y



∈L}}, (4.137)

which forms a sublattice of L. Denote the maximum elements of L and

min

(f) by max L and max L

min

(f), respectively.

Lemma 4.9.3. For X  max L

min

(f), it holds that

X ∈K

(f) ⇐⇒ X ∈L

min

(f).

Therefore, if max L∈L

min

(f), then K

(f)=L

min

(f).

Proof.IfX  max L

min

(f), the lattice (4.134) is a sublattice of L

min

(f).

Originally, the principal structure is deﬁned in the case of L =2

for a

ﬁnite set V , as follows. Let f :2

→ R be a submodular function:

f(X)+f(Y ) ≥ f(X ∪ Y )+f(X ∩ Y ),X,Y⊆ V,

with f(∅) = 0. Such a pair (2

,f) is called a submodular system. Given an

element v ∈ V , we denote by D(f; v) the minimum element of the distributive

lattice

min

(f; v)={X ⊆ V | v ∈ X, f(X) = min{f(Y ) | v ∈ Y ⊆ V }}. (4.138)

Since the relation + deﬁned by

v + v



⇐⇒ v ∈ D(f; v



)

is reﬂexive and transitive, the relation ∼ deﬁned by

v ∼ v



⇐⇒ v + v



+ v

254 4. Theory and Application of Mixed Matrices

is an equivalence relation, and determines a partition of V into equivalence

classes {V

, ···,V

}. A partial order  is induced among the equivalence

classes in such a way that V

 V

if and only if v + v



for v ∈ V

and v



∈ V

This decomposition, together with the partial order  among the blocks, is

called the principal structure of the submodular system (2

,f). We denote

this by P

(f). According to Birkhoﬀ’s representation theorem (Theorem

2.2.10), the principal structure P

(f) corresponds to a sublattice of 2

which we denote by L(P

(f)). This sublattice coincides with the principal

sublattice L

(f)forL =2

, as stated below.

Lemma 4.9.4. L(P

(f)) = L

(f) for a submodular function f :2

→ R.

Proof. L(P

(f)) is the sublattice of L =2

generated by {D(f; v) | v ∈ V },

whereas L

(f)isbyK

(f)={D(f ; X) | X ⊆ V }. Since {D(f ; v) | v ∈

V }⊆K

(f), we have L(P

(f)) ⊆L

(f). Conversely, for X = D(f; X) ∈

(f), we have X =



v∈X

D(f; v) ∈L(P

(f)) since D(f; X) ⊇ D(f; v) ⊇

{v} for v ∈ X. This implies L

(f) ⊆L(P

(f)).

Example 4.9.5. As an example of a submodular function we consider the

LM-surplus function p :2

→ Z associated with the LM-matrix A of Example

4.9.1, where C = {x

} and p(X)=ρ(X)+γ(X) −|X| as deﬁned in

(4.16). From the values of p shown in Fig. 4.23, we see that D(p; x

)={x

D(p; x

)={x

},andD(p; x

)={x

}. Hence P

(p) is given by:

}≺{x

}, {x

}≺{x

}.WehaveK

(p)={∅, {x

}, {x

}}

and L

(p)=K

(p) ∪{{x

}}. We may observe here that P

(p) agrees

with

I∈B

row

CCF

(I,C), the coarsest common reﬁnement of {P

CCF

(I,C) |

I ∈B

row

} that we considered in Example 4.9.1. Corollary 4.9.11 will reveal

that this is always the case. 2

4.9.3 Principal Structure of Generic Matrices

Before entering into the general case of LM-matrices we consider here the

principal structure of generic matrices. This special case deserves a separate

consideration not only because it is the origin of the main idea, but also

because it has an interesting application to the problem of making matrices

sparser.

Let A be a generic matrix with R =Row(A)andC = Col(A), and

row

= {I ⊆ R | rank A =rankA[I,C]=|I|} (4.139)

be the family of row-bases of A. We assume in this subsection that rank A =

|C|.

For each I ∈B

row

the submatrix A[I,C] is nonsingular, and the DM-

decomposition of A[I,C] determines a block-triangularization with nonsin-

gular diagonal blocks. Denote by P

(I,C) the pair of the partition of C

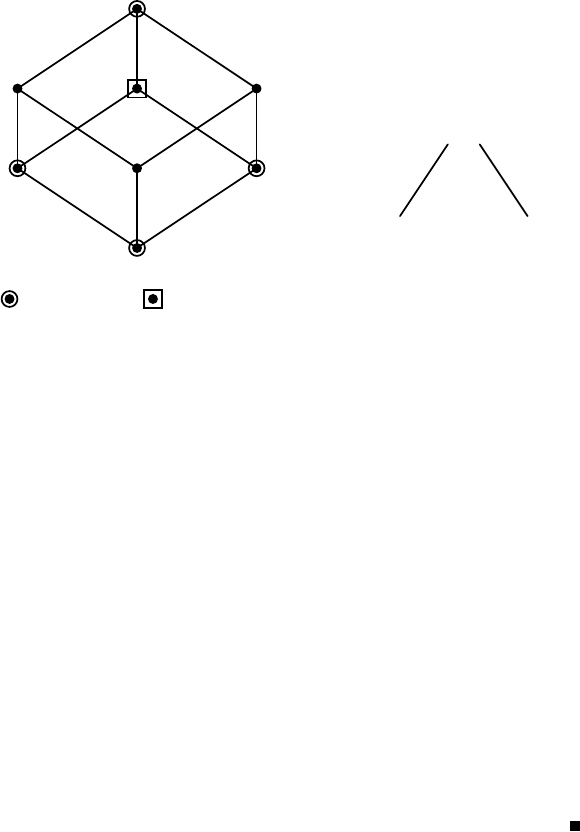
4.9 Principal Structures of LM-matrices 255

},p=2

}

p =3

}

p =3

} p =3

}

p =1

}

p =2

} p =3

∅,p=0

∈K

(p) ∈L

(p) \K

(p)

D(p; x

)={x

}

D(p; x

)={x

}

D(p; x

)={x

}

}{x

}

(p)

Fig. 4.23. The principal structure of the LM-surplus function p of the LM-matrix

in Example 4.9.1

and the partial order among the blocks in the DM-decomposition of the sub-

matrix A[I,C], and by

I∈B

row

(I,C) the coarsest partition of C which

is ﬁner than all P

(I,C) with I ∈B

row

The surplus function p

→ Z deﬁned as p

(X)=γ(X) −|X| for

X ⊆ C in (2.39) is submodular, and hence we may think of the principal

structure P

)ofp

, which we call the principal structure of the generic

matrix A. It is observed by Murota [210] that the principal structure P

)

of the surplus function p

is identical with the SP-decomposition introduced

by McCormick [190]. With this observation a result of McCormick [190] can

be formulated as follows.

Theorem 4.9.6. For a generic matrix A of full-column rank and its surplus

function p

→ Z, we have

I∈B

row

(I,C).

Proof. This is proven later as a special case of Corollary 4.9.11.

The principal structure P

), or rather the family {D(p

; j) | j ∈ C}

deﬁning P

), plays a key role in the algorithm of Hoﬀman–McCormick

[112] for making matrices optimally sparse.

Suppose we are given a matrix A =(A

) of full-column rank and we

want to ﬁnd a nonsingular matrix S =(S

) such that

A = AS has the

minimum number of nonzero entries. For a generic matrix A this problem has

a nice combinatorial answer with an eﬃcient algorithm, while for a general

numerical matrix it is NP-hard due to “unexpected” numerical cancellations.

256 4. Theory and Application of Mixed Matrices

The algorithm of Hoﬀman–McCormick [112] may be described as follows,

where C = Col(A)

∼

Row(S) and we ﬁx an arbitrary one-to-one correspon-

dence between Row(S) and Col(S).

Algorithm for optimally sparse matrix

A = AS

1. Fix a one-to-one mapping σ : C → R such that A

σ(j),j

=0forj ∈ C

(such σ exists since rank A = |C|).

2. For each k ∈ C, solve the system of equations in {S

| j ∈ D(p

; k)}:



j∈D(p

;k)



1(i = σ(k))

0(i ∈ σ(D(p

; k) \{k}))

(4.140)

and put S

=0forj ∈ C \D(p

; k).

3. Put

A = AS. 2

For the validity of the algorithm we have the following two lemmas.

Lemma 4.9.7. The matrix S constructed by the algorithm is nonsingular.

Proof.LetD

, ···, be the distinct elements among {D(p

; j) | j ∈ C},

and put X



| D

⊂ D

= D

} and C

= D

\ X

for t =1, 2, ···.

By construction, S is block-triangular with respect to the partition {C

} of

C (

∼

Row(S)

∼

Col(S)), and therefore it suﬃces to show that S[C

]

is nonsingular for each t. From (4.140) we have an identity: A[σ(D

),D

] ·

S[D

A[σ(D

),D

], which can be rewritten as



σ(X

) A

σ(C

) A









where

A[σ(X

),C

]=O and

A[σ(C

),C

]=I. In the above expression, A

A[σ(X

),X

] is nonsingular since A

σ(j),j

=0forj ∈ X

, and then it follows

that (A

− A

−1

= I. This implies that S

= S[C

]is

nonsingular.

Lemma 4.9.8. The matrix

A constructed by the algorithm contains the min-

imum number of nonzero entries.

Proof. Consider

A = AS for a nonsingular matrix S in general, and put

= {j | S

=0} for k ∈ C. By the nonsingularity of S, we may assume

k ∈ J

for all k ∈ C with the understanding of the above-mentioned one-

to-one correspondence between Row(S) and Col(S). The assumed genericity

of the nonzero entries of A implies that the number of the nonzero entries

in the column k of

A is not smaller than |{i ∈ R |∃j ∈ J

: A

=

0}| − |J

| +1 = p

) + 1, whereas this lower bound is attained in the

algorithm with J

= D(p

; k).

4.9 Principal Structures of LM-matrices 257

Example 4.9.9. The above argument is illustrated here for a generic matrix

A =

0 a

where the underlined entries indicate σ : C → R.WehaveD(p

; x

}, D(p

; x

)={x

},andD(p

; x

)={x

}, since p

(∅)=0,

({x

})=2,p

({x

})=4,p

({x

})=2,p

({x

})=3,p

({x

})=3,

({x

})=3,p

({x

}) = 2. By the algorithm above, the matrix A

is transformed to a sparser matrix

A = SA, where

S =

0 s

A =

¯a

1 0 0

¯a

1¯a

0 0 1

0¯a

¯a

The two boldface zeros in

A are created. The entries of S are determined

from

=1,

⎡

⎣

0 a

⎤

⎦

⎡

⎣

⎤

⎦

⎡

⎣

⎤

⎦

=1.

Computational aspects of this algorithm and its variants are reported in

Chang–McCormick [31, 32], McCormick [191], and McCormick–Chang [192].

4.9.4 Vertical Principal Structure of LM-matrices

Let A =

∈ LM(K, F ) be an LM-matrix with R =Row(A)and

C = Col(A), and B

row

⊆ 2

be the family of row-bases of A as in (4.139).

For I ∈B

row

the submatrix A[I,C] is an LM-matrix of full-row rank, and

the CCF of A[I,C] determines a block-triangularization with an empty ver-

tical tail. Denote by P

CCF

(I,C) the pair of the partition of C and the

partial order among the blocks in the CCF of the submatrix A[I,C], and

I∈B

row

CCF

(I,C) the coarsest partition of C which is ﬁner than all

CCF

(I,C) with I ∈B

row

. We also denote by L

CCF

(I,C) the sublattice

of 2

that corresponds to P

CCF

(I,C), and by

I∈B

row

CCF

(I,C) the sub-

lattice generated by {L

CCF

(I,C) | I ∈B

row

}. Note that L(P

CCF

(I,C)) =

CCF

(I,C)and

I∈B

row

CCF

(I,C)) =

I∈B

row

CCF

(I,C)

258 4. Theory and Application of Mixed Matrices

with the notation of Theorem 2.2.10.

The LM-surplus function p :2

→ Z deﬁned as p(X)=ρ(X)+γ(X)−|X|

for X ⊆ C in (4.16) is submodular, and hence we may think of the principal

structure of p. We name this the vertical principal structure of an LM-matrix

A. The following theorem of Murota [210] connects this with the family of

the CCF.

Theorem 4.9.10. For an LM-matrix A and its LM-surplus function p :

→ Z, we have

(p)=



I∈B

row

CCF

(I,C).

Proof. The proof is given later.

Theorem 4.9.10 can be reformulated in terms of the principal sublattice

and the corresponding partitions, as follows.

Corollary 4.9.11. For an LM-matrix A and its LM-surplus function p :

→ Z, we have

(p)=

I∈B

row

CCF

(I,C), P

(p)=

I∈B

row

CCF

(I,C). (4.141)

This corollary shows that the above result is a generalization of Theorem

4.9.6. We mention that the vertical principal structure P

(p)ofanLM-

matrix A ∈ LM(K, F ) can be found by an eﬃcient algorithm using arithmetic

operations in K.

Example 4.9.12. In Examples 4.9.1 and 4.9.5 we have seen an instance of

the identity (4.141). Note that P

(p) = P

CCF

(I,C)foreachI ∈B

row

. 2

Remark 4.9.13. The LM-surplus function p remains invariant against LM-

admissible transformations, whereas B

row

does not. For example, consider a

pair of LM-equivalent LM-matrices

(1)

110

001

00t

(2)

111

112

00t

We have B

(1)

row

= {{r

}, {r

}} and B

(2)

row

= B

(1)

row

∪{{r

}}. One of the

consequences of Theorem 4.9.10 is that



I∈B

row

CCF

(I,C) remains invariant

under LM-equivalence in spite of its apparent dependence on B

row

. 2

4.9 Principal Structures of LM-matrices 259

Proof of Theorem 4.9.10. We need to introduce the LM-surplus function

for submatrices of A =

. Putting R

=Row(Q)andR

=Row(T ),

deﬁne Γ :2

× 2

→ 2

, γ :2

× 2

→ Z,andρ :2

× 2

→ Z by

Γ (I,J)={i ∈ I |∃j ∈ J : T

=0},I⊆ R

,J ⊆ C,

γ(I,J)=|Γ (I,J)|,I⊆ R

,J ⊆ C,

ρ(I,J)=rankQ[I,J],I⊆ R

,J ⊆ C.

Then for I ⊆ R the LM-surplus function p

→ Z of the submatrix

A[I,C] is given by

(J)=ρ(I ∩R

,J)+γ(I ∩R

,J) −|J|,J⊆ C.

We have

CCF

(I,C)=L

min

)=K

),I∈B

row

, (4.142)

by the construction of the CCF (cf. §4.4.3) and Lemma 4.9.3. Hence, in order

to prove Theorem 4.9.10, we shall reveal the relation between K

)and

), i.e., the relation between D(p

; X)andD(p

; X), deﬁned in (4.135).

Lemma 4.9.14. For X ⊆ C and I ⊆ R we have D(p

; X) ⊆ D(p

; X).

Proof.PutD

= D(p

; X)andD

= D(p

; X). By Proposition 2.1.9(2) we

have

ρ(R

,J) − ρ(R

,J ∩ J



) ≥ ρ(I



,J ∪ J



) − ρ(I





),I



⊆ R

,J,J



⊆ C.

Similarly, it can be shown that

γ(R

,J) − γ(R

,J ∩ J



) ≥ γ(I



,J ∪ J



) − γ(I



),I



⊆ R

,J,J



⊆ C.

These inequalities imply

) − p

∩ D

) ≥ p

∪ D

) − p

The right-hand side of this is nonnegative since X ⊆ D

∪ D

and D

∈

min

; X). Hence follows p

) ≥ p

∩D

). This implies D

∩D

∈

min

; X), from which follows D

= D

∩ D

by the minimality of D

Therefore, D

⊆ D

Lemma 4.9.15. For X ⊆ C, there exists I ∈B

row

such that D(p

; X)=

D(p

; X).

Proof.PutD

= D(p

; X), C



= C \ D

,andΓ

= Γ (R

(i) First choose I

⊆ R

such that

rank Q[R

]=rankQ[I

]=|I

260 4. Theory and Application of Mixed Matrices

The row vectors of Q[R

\ I

] can be expressed as linear combinations

of those of Q[I

], i.e., Q[R

\ I

]=SQ[I

] for some matrix S

over K. If we put

Q =



\ I

−SI



Q, (4.143)

we have

Q[R

\ I

]=O. Furthermore, put

A =





⎛

⎜

⎝



= C \ D

Q[I

]

Q[I



]

\ I

Q[R

\ I



]

T [Γ

] T[Γ



]

\ Γ

OT[R

\ Γ



]

⎞

⎟

⎠

, (4.144)

which is an LM-matrix. Denoting by ¯p

the LM-surplus function associated

with

A[I,C]wehave¯p

(J)=p

(J)ifI

⊆ I ⊆ R and J ⊆ C.

(ii) Next choose I

⊆ Γ

⊆ R

such that

rank A[R, D

]=rankA[I

∪ I

]=|I

| + |I

This is equivalent, by (4.143), to

rank

A[R, D

]=rank

A[I

∪ I

]=|I

| + |I

|. (4.145)

(iii) Put



= R \ (I

∪ Γ

)=(R

\ I

) ∪ (R

\ Γ

and note that

A[R



]=O as seen in (4.144). We claim

rank

A[R



]=|C



|. (4.146)

To compute the rank of

A[R



] by Theorem 4.2.5, we consider ¯p



(J),

J ⊆ C



. Since

¯p



(J)=rank

Q[R

\ I

,J]+γ(R

\ Γ

,J) −|J|,

by the deﬁnition, and furthermore

rank

Q[R

\ I

,J]=rank

Q[R

∪ J] −|I

=rankQ[R

∪ J] − rank Q[R

γ(R

\ Γ

,J)=γ(R

∪ J) − γ(R

by the choice of I

and the deﬁnition of Γ

,wehave

¯p



(J)=p

∪ J) − p