Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

4.9 Principal Structures of LM-matrices 261

This is nonnegative for all J ⊆ C



since X ⊆ D

∪J and D

∈L

min

; X).

Hence follows (4.146) from Theorem 4.2.5. Therefore there exists I

⊆ R



such that

rank

A[R



]=rank

A[I



]=|I

| = |C



|. (4.147)

(iv) We claim that I = I

∪I

belongs to B

row

. By (4.145), (4.147),

and

A[I

]=O,wesee

rank A[I,C]=rank

A[I,C]=|I|. (4.148)

On the other hand, since

A[R



]=O and

A[R



] is of full-column rank

by (4.147), we see

rank A =rank

A =rank

A[R\R



]+|C



| = |I

|+|I

| = |I|. (4.149)

Combination of this and (4.148) shows that I ∈B

row

(v) Furthermore we claim that

) = min{p

(J) | J ⊆ C}. (4.150)

By the deﬁnitions of I

and I

,wehave

)=p

∪I

)=|I

| + |I

|−|D

We also have

min{p

(J) | J ⊆ C} = |I|−|C|

from (4.148) and Theorem 4.2.5. Noting the relation |I

| + |I

|−|D

| =

|I|−|C| due to (4.147), we establish (4.150).

(vi) Since X ⊆ D

, (4.150) means D

∈L

min

; X). The minimality of

= D(p

; X) then implies that D

⊇ D

. The other direction D

⊆ D

already shown in Lemma 4.9.14.

With the above lemmas we can now prove Theorem 4.9.10. It follows from

Lemma 4.9.14 that D(p

; X)=X implies D(p

; X)=X. Hence, K

) ⊆

) holds for any I ⊆ R. On the other hand, Lemma 4.9.15 implies

) ⊆



I∈B

row

). Therefore, we have



I∈B

row

which establishes Theorem 4.9.10 when combined with the relation (4.142).

4.9.5 Horizontal Principal Structure of LM-matrices

Let A =

∈ LM(K, F ; m

,n) be an LM-matrix with R =Row(A)

and C = Col(A). In the previous subsection we have characterized the com-

mon reﬁnement of the CCF of all A[I,C] with I ∈B

row

by means of the

262 4. Theory and Application of Mixed Matrices

principal structure of the LM-surplus function p :2

→ Z. Here we are con-

cerned with the “transpose version” of the problem by considering the family

of submatrices A[R, J]forJ ∈B

col

, where

col

= {J ⊆ C | rank A =rankA[R, J]=|J|}. (4.151)

The present problem is not reduced to the previous one, since the trans-

pose of an LM-matrix is no longer an LM-matrix. The transpose of an LM-

matrix, however, may be regarded as a partitioned matrix, for which we have

developed a general framework in §4.8. In particular, the function q to be

introduced in place of p is essentially the same as the PE-surplus function

associated with the transpose of A.

We regard the m

× n matrix Q as a representation of a linear transfor-

mation from K

to the dual space V

∗

∼

of V

∼

.LetL be the

set of the pairs of a subspace W of V

and a subset I of R

=Row(T ), i.e.,

L = {(W, I ) | W : subspace of V

,I⊆ R

which forms a modular lattice with the operations ∧ and ∨ deﬁned by

) ∧ (W

)=(W

∩ W

∩ I

)

) ∨ (W

)=(W

+ W

∪ I

)

for W

⊆ V

and I

⊆ R

(h =1, 2). We deﬁne κ, q : L→Z by

κ(W, I )=|{j ∈ C | Q

/∈ W

⊥

or ∃i ∈ I : T

=0}|, (W, I) ∈L, (4.152)

q(W, I)=κ(W, I) − dim W −|I|, (W, I) ∈L, (4.153)

where Q

denotes the column vector of Q indexed by j ∈ C, T

is the (i, j)

entry of T ,andW

⊥

is the subspace of V

∗

annihilating W , i.e.,

⊥

= {v ∈ V

∗

|w, v =0, ∀w ∈ W },

in which ·, ·means the inner product (pairing). Note that Q

∈ V

∗

Remark 4.9.16. For A =

∈ LM(K, F ; m

,n) we regard A

as a

partitioned matrix (4.113) with the parameters

μ = n, ν =1+m

=1(α =1, ···,μ),n



(β =1)

1(β =2, ···,ν).

The function q deﬁned above is essentially the same as the PE-surplus func-

tion p

deﬁned by (4.120), in which “W ∈W” is replaced by “(W, I) ∈L”,

“



α=1

dim(A

W )” by “κ(W, I)”, and “dim W ” by “dim W + |I|”. 2

The following identity holds true.

4.9 Principal Structures of LM-matrices 263

Lemma 4.9.17. For an m × n LM-matrix A,

rank A = min{q(W, I) | (W, I) ∈L}+ m.

Proof. The CCF of A gives a proper block-triangularization under an LM-

admissible transformation, which is a PE-transformation for A

. Then The-

orem 4.8.6 shows the validity of the claimed identity.

For J ∈B

col

the submatrix A[R, J] is an LM-matrix of full-column rank.

Let L

CCF

(R, J) denote the sublattice of L that corresponds to the CCF

of A[R, J] in the sense of Proposition 4.8.12 (applied to the transpose of

A[R, J]). Note that L

CCF

(R, J) contains max L =(V

), since the CCF

of A[R, J] has an empty horizontal tail.

The function q : L→Z is submodular, and hence we may think of

the principal structure K

(q) as well as the principal sublattice L

(q). We

name this the horizontal principal structure of an LM-matrix A. The following

theorem of Iwata–Murota [145] connects this with the family of CCF.

Theorem 4.9.18. For an LM-matrix A and the function q : L→Z of

(4.153), we have

(q)=



J∈B

col

CCF

(R, J), L

(q)=

J∈B

col

CCF

(R, J).

Proof. The proof is given later.

Example 4.9.19. Let us illustrate the above result for an LM-matrix

A =

01111

02020

000t

0 t

where C = {x

}, R

= {y

} and R

= {z

}. The whole

matrix A is the horizontal tail of its CCF.

As is easily veriﬁed, we have

(q)={(0, ∅), (V

, ∅), (V

, ∅), (0,Z

), (V

)},

where Z

= {z

}, Z

= {z

},andV

and V

are the 1-dimensional vec-

tor spaces spanned by (0, 1) ∈ V

and (2, −1) ∈ V

, respectively. Note, for

example, that q(V

)=q(V

)=2andq(V

) = 1. The princi-

pal structure K

(q) and the principal sublattice L

(q) are illustrated in

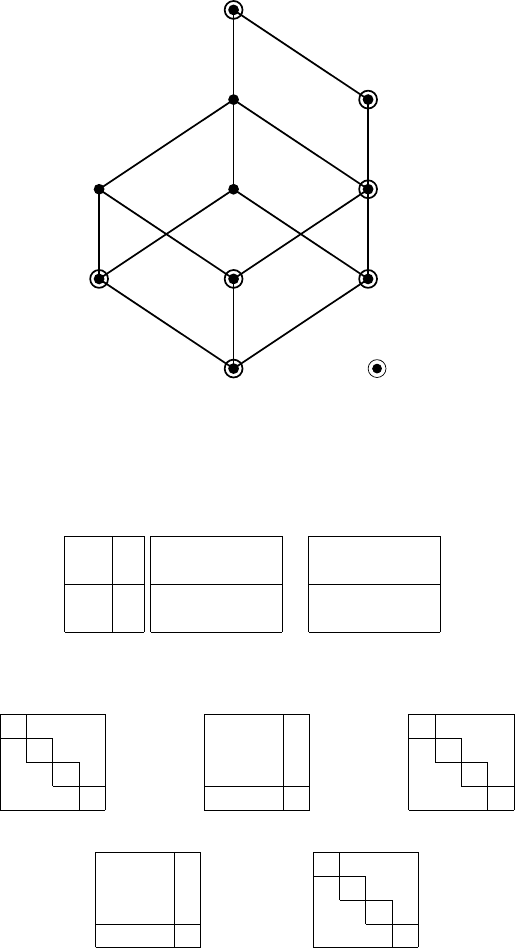
Fig. 4.24.

On the other hand, we have B

col

= {J

| h =1, ···, 5} with J

= C \{x

}

for h =1, ···, 5. In view of

264 4. Theory and Application of Mixed Matrices

(0, ∅)

, ∅)

(0,Z

)

, ∅)(V

)

∈K

(q)

Fig. 4.24. Principal sublattice L

(q) of the horizontal principal structure of the

LM-matrix in Example 4.9.19

A =

2 −1

01111

02020

000t

0 t

02020

00202

000t

0 t

we see that the CCF of A[R, J

], denoted by

, are given as follows:

2 2

022

0 t

2 2

022

0 t

2 2

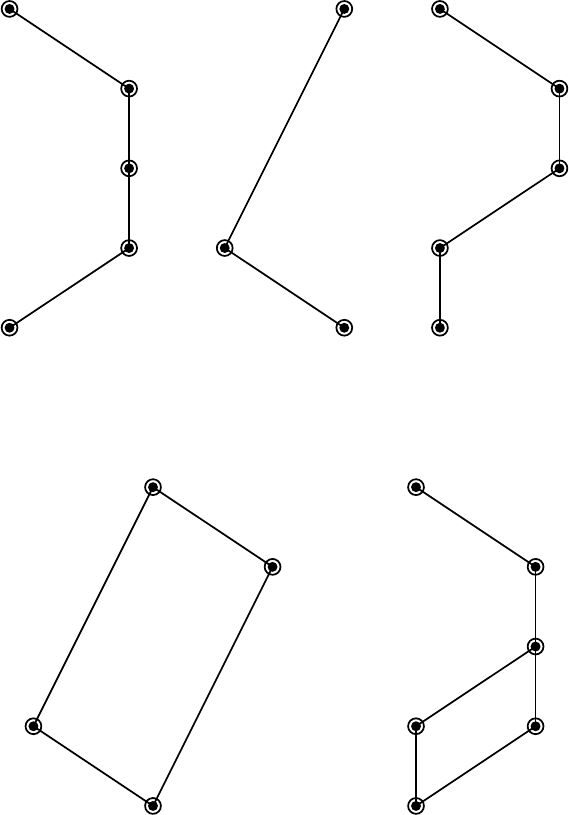
Figure 4.25 illustrates the sublattices L

CCF

(R, J

)forh =1, ···, 5, which

correspond to

above. For example, the height of L

CCF

(R, J

)isfour,

since

is in a block-triangular form with four diagonal blocks, and a par-

allelepiped appears in L

CCF

(R, J

), since the (3, 4) entry of

is zero. We

4.9 Principal Structures of LM-matrices 265

(0, ∅)

(0,Z

)

(0, ∅)

, ∅)

)

(0, ∅)

, ∅)

)

CCF

(R, J

) L

CCF

(R, J

) L

CCF

(R, J

)

(0, ∅)

, ∅)

)

(0, ∅)

, ∅)(0,Z

)

CCF

(R, J

) L

CCF

(R, J

)

Fig. 4.25. The Hasse diagrams for L

CCF

(R, J

)’s in Example 4.9.19.

266 4. Theory and Application of Mixed Matrices

can easily observe that K

(q) agrees with



h=1

CCF

(R, J

). Furthermore

(q) = L

CCF

(R, J) for any single J ∈B

col

. 2

Remark 4.9.20. We intend that the horizontal principal structure is de-

ﬁned primarily for an LM-matrix of full-row rank, while the vertical princi-

pal structure for an LM-matrix of full-column rank. It will be natural to ask:

For an LM-matrix A of rank r in general what is the coarsest simultaneous

decomposition of the row and the column sides which is ﬁner than any de-

composition induced by the CCF of an r ×r nonsingular submatrix of A?A

simple combination of the results for the horizontal and vertical structures

gives a solution to this question if A is already in the CCF. All the diagonal

blocks of A should remain in the CCF of an r×r nonsingular submatrix of A.

The reﬁnement of the horizontal tail of A is given by the principal structure

of q while the principal structure of p gives the reﬁnement of the vertical tail.

This explains, at the same time, why we name the former the “horizontal

principal structure” and the latter the “vertical principal structure.” 2

Proof of Theorem 4.9.18. We need to deﬁne the function “q” of (4.153)

for submatrices of A =

. Deﬁne κ : L×2

→ Z by

κ((W, I ),J)=|{j ∈ J | Q

/∈ W

⊥

or ∃i ∈ I : T

=0}|, (W, I) ∈L,J⊆ C.

Then for J ⊆ C the function q

: L→Z associated with the submatrix

A[R, J] by (4.153) is given by

(W, I )=κ((W, I),J) − dim W −|I|, (W, I) ∈L.

Lemma 4.9.21.

)+q

) ≥ q

∩J

∨ X

)+q

∪J

∧ X

∈L,J

⊆ C (i =1, 2).

Proof. With Ω((W, I ),J)={j ∈ J | Q

∈ W

⊥

,T[I,j]=0} we have

(W, I )=|J|−|Ω((W, I),J)|−dim W −|I|, (W, I ) ∈L,J⊆ C.

Noting

Ω(X

) ∩ Ω(X

)=Ω(X

∨ X

∩ J

Ω(X

) ∪ Ω(X

) ⊆ Ω(X

∧ X

∪ J

we obtain

|Ω(X

)| + |Ω(X

= |Ω(X

) ∩ Ω(X

)| + |Ω(X

) ∪ Ω(X

≤|Ω(X

∨ X

∩ J

)| + |Ω(X

∧ X

∪ J

)|.

4.9 Principal Structures of LM-matrices 267

This implies the desired inequality.

Consider a submatrix A[R, J]forJ ∈B

col

. Since A[R, J] is of full-column

rank, having no horizontal tail in its CCF, we have

)=L

min

)=L

CCF

(R, J) (4.154)

by Lemma 4.9.3 and the arguments in §4.8.

Lemma 4.9.22. For X ∈Land J ⊆ C we have D(q

; X)  D(q

; X).

Proof.PutD

= D(q

; X)andD

= D(q

; X). By Lemma 4.9.21 we have

) − q

∧ D

) ≥ q

∨ D

) − q

The right-hand side is nonnegative since X  D

∨D

and D

∈L

min

; X).

This implies D

 D

. See the proof of Lemma 4.9.14.

Lemma 4.9.23. For X ∈L, there exists J ∈B

col

such that D(q

; X)=

D(q

; X).

Proof.PutD

=(W

)=D(q

; X). By an LM-admissible transforma-

tion that takes a basis in V

compatible with W

, the matrix A can be

transformed to the following form:

A =





⎛

⎜

⎝



Q[R



]

Q[R



,K]

Q[H, K]



T [R



] T [R



,K]

OT[I

,K]

⎞

⎟

⎠

where |H| =dimW

, R



=Row(

Q) \ H, R



= R

\ I

K = {j ∈ C | Q

/∈ W

⊥

or ∃i ∈ I

: T

=0}

and C



= C \ K. We put

R =Row(

A).

Putting R



= R



∪ R



we claim that

rank

A[R



]=|R



|. (4.155)

This can be shown as follows. Since

A[H ∪ I



]=O,itholdsthat

rank

A[R



]=rank

R, C



]=rankA[R, C



]. (4.156)

Applying Lemma 4.9.17 to A[R, C



] and noting that Q

∈ W

⊥

and

T [I

,j]=0 for all j ∈ C



, we obtain

268 4. Theory and Application of Mixed Matrices

rank A[R, C



] = min{q



(W, I ) | (W, I) ∈L}+ m

= min{q



(W, I ) | W ⊇ W

,I⊇ I

} + m. (4.157)

For W ⊇ W

and I ⊇ I

,wehave

κ((W, I ),C



)=κ((W, I ),C) −|K| = κ((W, I),C) − κ((W

),C).

Hence it holds that



(W, I )=κ((W, I),C



) −|I|−dim W

= q

(W, I ) − q

) −|I

|−dim W

, (4.158)

in which

(W, I ) − q

) ≥ 0 (4.159)

by the deﬁnition of D

=(W

) and (W, I) , X. Combining (4.156),

(4.157), (4.158), (4.159), and m −|I

|−dim W

= |R



|, we obtain (4.155).

Therefore there exists J



⊆ C



such that

rank

A[R



]=|R



| = |J



At the same time, there exists J

⊆ K such that

rank

A[H ∪ I

,K]=rank

A[H ∪ I

]=|J

Put J = J



∪ J

.Wehave

rank

R, J]=|J|, (4.160)

since both

A[R



]and

A[H ∪ I

] are of full-column rank, and

A[H ∪



]=O. On the other hand, since

A[R



] is of full-row rank,

rank

A =rank

A[R



]+rank

A[H ∪ I

,K]=|J



| + |J

| = |J|.

Thus we obtain J ∈B

col

Applying Lemma 4.9.17 to A[R, J] and using rank A[R, J]=rank

R, J]

and (4.160), we obtain

min{q

(Y ) | Y ∈L}= |J|−m,

which together with q

)=|J

|−|I

|−dim W

= |J|−m and X  D

implies

) = min{q

(Y ) | X  Y ∈L}.

Thus we obtain D

, D(q

; X), which completes the proof since we have

already shown D

 D(q

; X) in Lemma 4.9.22.

We are now ready to complete the proof of Theorem 4.9.18. It follows from

Lemma 4.9.22 that D(q

; X)=X implies D(q

; X)=X. Hence, K

) ⊆

) holds for any J ⊆ C. On the other hand, from Lemma 4.9.23,

X = D(q

; X) implies the existence of J ∈B

col

such that X = D(q

; X).

Hence



J∈B

col

which establishes Theorem 4.9.18 when combined with (4.154).

4.9 Principal Structures of LM-matrices 269

Notes. A series of theorems described in this section, due to McCormick

[190], Murota [210], and Iwata–Murota [145], clariﬁed a relationship between

the two general decomposition principles for submodular functions, i.e., be-

tween the Jordan–H¨older-type theorem of §2.2.2 and the principal structure

of §4.9.2, in the context of block-triangularization of matrices. The combina-

torial essence of those theorems has been extracted by Iwata–Murota [143]

and Iwata [139] without reference to matrices.

5. Polynomial Matrix and Valuated Matroid

Matrices consisting of polynomials or rational functions play fundamental

roles in various branches in engineering. Combinatorial properties of poly-

nomial matrices are abstracted in the language of valuated matroids. This

chapter is mostly devoted to an exposition of the theory of valuated ma-

troids, whereas the ﬁrst section describes a number of canonical forms of

polynomial/rational matrices that are amenable to combinatorial methods of

analysis to be explained in Chap. 6.

5.1 Polynomial/Rational Matrix

Matrices consisting of polynomials or rational functions play fundamental

roles in various branches in engineering (Gohberg–Lancaster–Rodman [95]).

In dynamical system theory, for example, a linear time-invariant system is

described by a polynomial matrix called the system matrix (the Laplace

transform of the state-space equations), or by a rational function matrix

called the transfer function matrix (Rosenbrock [284], Vidyasagar [331]).

In this section three canonical forms of polynomial/rational matrices are

described: the Smith form of polynomial matrices, the Smith–McMillan form

at inﬁnity of rational matrices, and the Kronecker form of matrix pencils.

5.1.1 Polynomial Matrix and Smith Form

Let A(s)=(A

(s)) be an m × n polynomial matrix with A

(s) being a

polynomial in s with coeﬃcients from a certain ﬁeld F (i.e., A

(s) ∈ F [s]).

Typically F is the real number ﬁeld R.

The kth determinantal divisor, denoted by d

(s), is deﬁned to be the

greatest common divisor of all the minors of order k:

(s)=gcd{det A[I,J] ||I| = |J| = k} (k =0, 1, ···,r), (5.1)

where r =rankA and d

(s) = 1 by convention. The kth invariant factor (or

invariant polynomial), denoted by e

(s), is deﬁned by

(s)=

(s)

k−1

(s)

(k =1, ···,r). (5.2)

K. Murota, Matrices and Matroids for Systems Analysis,

Algorithms and Combinatorics 20, DOI 10.1007/978-3-642-03994-2

 Springer-Verlag Berlin Heidelberg 2010