Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

4.4 Combinatorial Canonical Form of LM-matrices 191

3. For each DM-component

, which is an LM-matrix of a smaller size:



(θ)



ﬁnd its CCF:

k;ij

| 1 ≤ i, j ≤ D

)

where

k;ij

= O for i>j,andS

is a constant matrix representing the

row transformation of (4.35) and the column permutation is suppressed

for simplicity. Accordingly put z

=(z

k;1

, ···, z

k;D

4. Each time the value of θ is given, solve the subproblems as follows:

for k := D downto 1 do

Put

:= S

[

− (

k,k+1

k+1

+ ···+

)].

for i := D

downto 1 do

Solve

k;ii

k;i

− (

k;i,i+1

k;i+1

+ ···+

k;iD

) (4.68)

for z

k;i

, where (

k;1

, ···,

k;D

. 2

It should be noted that there is no need to keep S

explicitly. In solving (4.68),

the LU-decomposition of

k;ii

is to be determined each time θ is given.

4.4.6 Application of CCF

The decomposition technique based on the CCF, as described in §4.4.5, is ap-

plied to a series of example problems: an electrical network, the hypothetical

ethylene dichloride production system of Example 3.1.3, the reactor-separator

model of Example 4.3.10, the hydrogen production system of Example 4.3.11,

and a collection of test matrices taken from the Harwell–Boeing database.

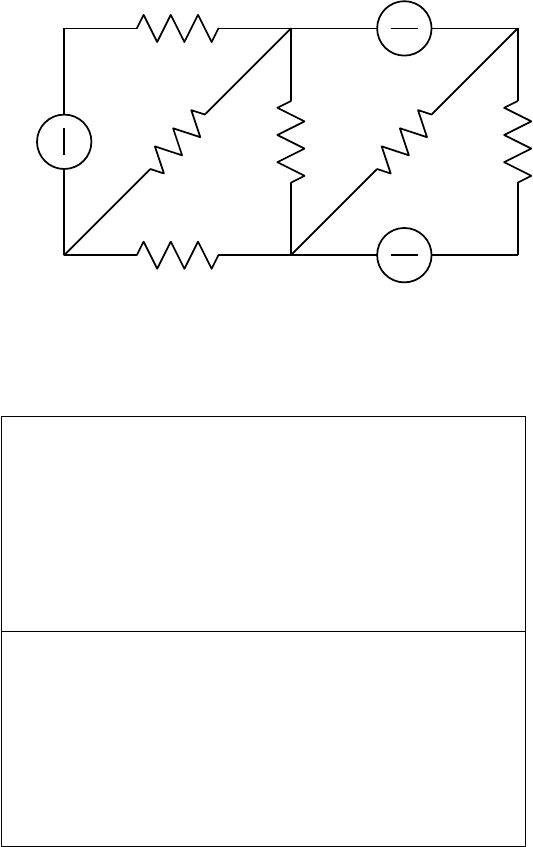
Example 4.4.14. The decomposition by the CCF is applied to a simple

electrical network of Fig. 4.19, which is taken from Nakamura [243, Example

4.1.3]. It consists of six resistors of resistances r

(branch i)(i =1, ···, 6), and

three voltage-controlled current sources (branch i) with mutual conductances

(i =7, 8, 9); the current sources of branches 7, 8, and 9 are controlled

respectively by the voltages across branches 2, 4, and 5. Then the current ξ

in and the voltage η

across branch i (i =1, ···, 9) are to satisfy a system of

equations of the form (3.2) with the coeﬃcient matrix

192 4. Theory and Application of Mixed Matrices

- 

6 6

 

= g



= g



Fig. 4.19. An electrical network of Example 4.4.14

A =

100000−10 0

011000 1 0 0

010110 1 0−1

000001 0 0−1

010100 1 1 0

0 −11100000

−101100−10 0

0001−10 0−10

0000−1 −10 0−1

−1

−1 g

The unique solvability of the network reduces to the nonsingularity of the

matrix A.

We will regard r

(i =1, ···, 6) and g

(i =7, 8, 9) as real numbers which

are algebraically independent over the ﬁeld of rationals. Then we have A ∈

MM(Q, R;18, 18). Here we would rather treat A as an LM-matrix, just as

we did in Example 4.3.9, by multiplying the last 9 rows by independent

transcendentals. That is, we multiply the last 9 equations by transcendental

numbers and express the modiﬁed coeﬃcient, which we denote also as A,in

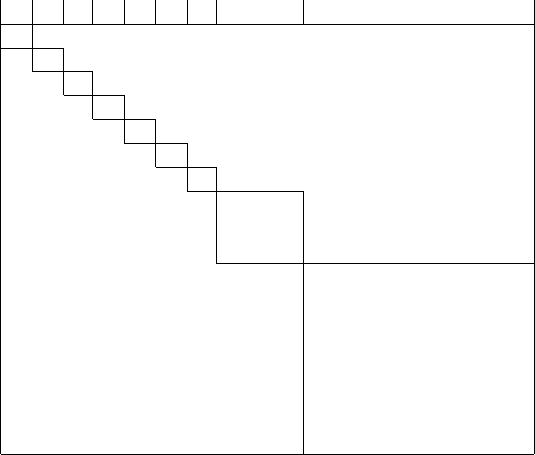
4.4 Combinatorial Canonical Form of LM-matrices 193

the form of A =

with Q being the ﬁrst 9 rows and T being the last 9

rows: A ∈ LM(Q, R;9, 9, 18).

Then the CCF of A is found to be

−1 −111

−1 r

1 −1

−1 −11

−1 −1 −1

−1 r

1 −1

01−1 111

−1 r

0 −1

101000 1 0

100010 1 1

0 −10101 0 0

−10000 0 0

00r

−10 0 0 0

0000r

−10 0

0 g

0000−10

00000g

0 −1

It has empty tails (C

= ∅, R

∞

= ∅) and nine square diagonal blocks; the

partial order among the column sets are shown in Fig. 4.20. 2

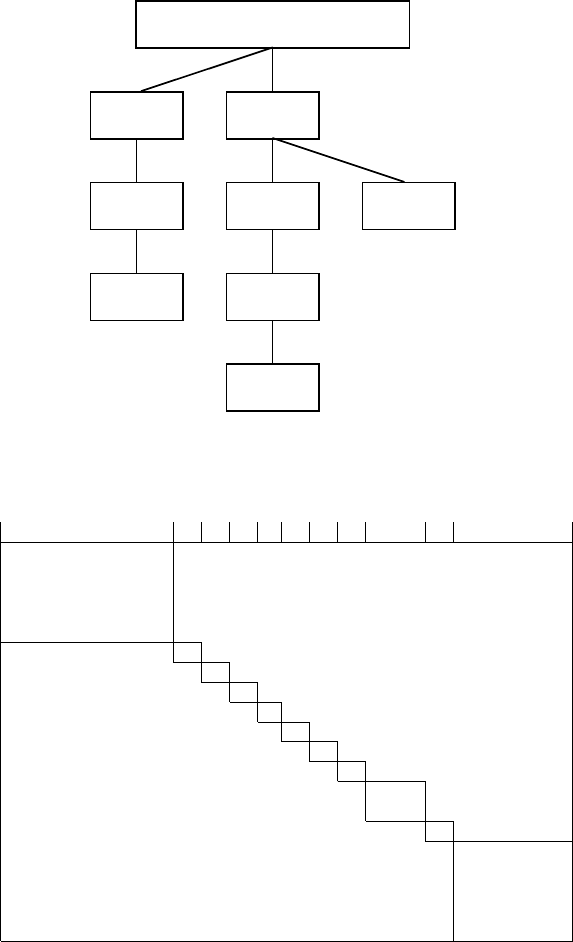
Example 4.4.15. In Example 4.3.8 we have seen that the graph-theoretic

method is not suﬃcient for the analysis of the hypothetical ethylene dichlo-

ride production system of Example 3.1.3. Though the DM-decomposition

(Fig. 4.11) can be useful to localize the source of singularity, it fails to

fully identify the rank structure of the Jacobian matrix. Here we apply

the CCF-decomposition technique to the associated LM-matrix given in

Fig. 4.12. The CCF, shown in Fig. 4.21, contains a 5 × 6 horizontal tail

= {w

,x,u

},a5× 4 vertical tail C

∞

= {w

and nine nonsingular blocks C

= {u

}, C

= {u

}, C

= {u

}, C

= {u},

= {u

}, C

= {u

}, C

= {u

}, C

= {w

}, C

= {u

}.The

partial order among the nonsingular blocks is given by C

≺ C

, C

≺ C

. The existence of the nonempty tails shows the rank deﬁciency of

the matrix. 2

Example 4.4.16. The decomposition technique described in §4.4.5 is ap-

plied to the reactor-separator model used in Example 4.3.10. The Jacobian

matrix, say A, is regarded as a mixed matrix, i.e., A ∈ MM(Q, F ; 120, 120).

194 4. Theory and Application of Mixed Matrices

,η

,ξ

,η

,ξ

,η

,ξ

Fig. 4.20. Partial order of Example 4.4.14

∞

u u

1 −1

y 1 −1

−11

1 −1

−t

⇑ 1 −1

horizontal tail −1

−1 −11

−1 1

1 −1

−t

1 −1

u 1

vertical tail ⇒ 1 −1

−t

u −t

Fig. 4.21. CCF of the LM-matrix associated with Jacobian matrix of (3.5) (chem-

ical process simulation in Example 3.1.3)

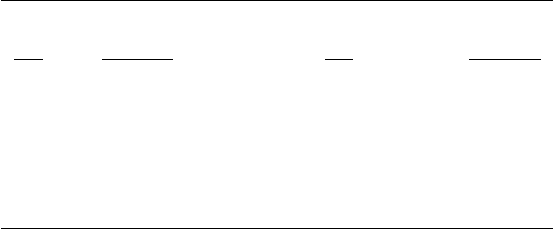
4.4 Combinatorial Canonical Form of LM-matrices 195

The DM-decomposition yields four nontrivial blocks involving more than

one unknown variable. The maximum size of the blocks is 25. See Table 4.2.

The CCF of the corresponding LM-matrix

A ∈ LM(Q, F ; 120, 120, 240)

in the sense of (4.4) provides a decomposition of the augmented system of

equations with 120 auxiliary variables. The CCF of

A has empty tails and

ﬁve nontrivial blocks, the maximum size of which being equal to 17. In Ta-

ble 4.2, the DM-decomposition of A and the CCF of

A are compared, where

| (the number of rows of the T -part of each block) is indicated in brack-

ets. Recall that the substantial size of a subproblem can be measured by

min(|C

|, |R

|) in (4.66).

The more compact transformation (4.6) to another LM-matrix, say

cpt

is also applied to A, for which m

(number of mixed rows) = 85, m

(number

of purely constant rows) = 34, m

(number of purely symbolic rows) = 1

in the notation of (4.5). Hence we obtain

cpt

∈ LM(Q, F ; 119, 86, 205). As

expected, the CCF of

cpt

agrees with that of

A up to singleton blocks. The

matrix

cpt

, the DM-decomposition and the CCF of

cpt

are depicted in

Fig. 4.22. 2

Table 4.2. Decompositions for the reactor-separator model (Example 4.4.16)

DM-decomposition of CCF of

A ∈ MM(Q, F ; 120, 120)

A ∈ LM(Q, F ; 120, 120, 240)

size

#blocks size #blocks

= C

+ C

]

25117=8+9[9]1

10115=6+9[6]1

9214=4+10[9]1

8=0+8 [4] 1

5=0+5 [5] 1

1 67 1 181

Example 4.4.17. The decomposition technique is applied to the problem of

the industrial hydrogen production system described in Example 4.3.11. The

Jacobian matrix A is thought of as a mixed matrix: A ∈ MM(Q, F ; 544, 544).

The CCF of the corresponding LM-matrix

A ∈ LM(Q, F ; 544, 544, 1088) in

the sense of (4.4) has empty tails and contains 23 nontrivial blocks with

more than one variable. The DM-decomposition of A and the CCF of

A are

summarized in Table 4.3. Note that the substantial sizes of the subproblems

in terms of min(|C

|, |R

|) are much smaller than those obtained by the

DM-decomposition. 2

196 4. Theory and Application of Mixed Matrices

0 50 100 150 200

-200

-150

-100

-50

LM-matrix

cpt

∈ LM(Q, F ; 119, 86, 205)

0 50 100 150 200

-200

-150

-100

-50

DM-decomposition of

cpt

0 50 100 150 200

-200

-150

-100

-50

CCF of

cpt

Fig. 4.22. LM-matrix

cpt

and its decompositions in Example 4.4.16 (reactor-

separator model)

4.4 Combinatorial Canonical Form of LM-matrices 197

Table 4.3. Decompositions for the hydrogen production system (Example 4.4.17)

DM-decomposition of CCF of

A ∈ MM(Q, F ; 544, 544)

A ∈ LM(Q, F ; 544, 544, 1088)

size

#blocks size #blocks

= C

+ C

]

104 1 114 = 75 + 39 [ 75 ] 1

28 1 24 = 15 + 9 [ 15 ] 1

23 1 18 = 10 + 8 [ 10 ] 1

14 1 14 = 8 + 6 [ 8 ] 1

1056=4+2[4]1

814=2+2[2]15

672=1+1[1]3

1 240 1 846

Example 4.4.18. A collection of matrices are taken from the Harwell–

Boeing database (Duﬀ–Grimes–Lewis [61, 62]), Problems IMPCOL and

WEST in particular, for test LM-matrices. Each matrix is thought of as

a mixed matrix, where integer entries of absolute value ≤ 10 are included

in the Q-part and the remaining entries are put into the T -part. The re-

sulting mixed matrix is then converted into an LM-matrix according to the

compact transformation (4.6). Table 4.4 summarizes properties of the test

LM-matrices. All the matrices are square.

Table 4.4. LM-matrices made from Harwell–Boeing matrices (Example 4.4.18)

Problem # Cols # Q-Rows # T -Rows #Entries #Entries

(n) (m

) (m

) in Q in T

IMPCOL A 228 171 57 338 276

IMPCOL B 89 58 31 137 194

IMPCOL C 154 136 18 399 35

IMPCOL D 483 425 58 1255 116

IMPCOL E 364 223 141 566 1015

WEST0067 86 31 55 94 238

WEST0132 211 93 118 203 368

WEST0156 229 135 94 264 244

WEST0167 262 115 147 244 452

Table 4.5 describes the block structures of the DM-decompositions and

the CCF of those matrices. It turned out, in particular, that all the LM-

matrices are nonsingular.

198 4. Theory and Application of Mixed Matrices

Table 4.5. Decompositions of the LM-matrices in Example 4.4.18

Problem Rank DM-decomp. CCF

size # blocks size # blocks

IMPCOL A 228 30 1 27 1

12 1 10 1

2929

1 168 1 173

IMPCOL B 89 66 1 45 1

123144

IMPCOL C 154 8141

1 125 1 150

IMPCOL D 483 115 1 51

1 368 1 472

IMPCOL E 364 73 1 70 1

36 1 27 1

19 1 10 1

2121

1 234 1 255

WEST0067 86 85 1 85 1

1111

WEST0132 211 127 1 115 1

184196

WEST0156 229 35 1 32 1

1 194 1 197

WEST0167 262 129 1 117 1

1 133 1 145

Table 4.6. Behavior of the CCF algorithm

Problem # Pivots # Base Change of

exchanges #Entries

IMPCOL A 787 6 −60

IMPCOL B 146 0 −8

IMPCOL C 6426 1 −144

IMPCOL D 76096 3 +24

IMPCOL E 2015 16 +157

WEST0067 21 0 +9

WEST0132 332 4 −14

WEST0156 227 6 −21

WEST0167 334 5 −22

4.4 Combinatorial Canonical Form of LM-matrices 199

Table 4.6 shows some data about the behavior of the CCF algorithm. The

ﬁrst column counts the total number of pivoting operations and the second

the total number of pairs (i

) ∈ L ∩ E

in Step 3. The third column

designates diﬀerence of the number of nonzero Q-entries in the CCF and in

the input LM-matrix. The data is based on an implementation of a minor

variant of the CCF algorithm (called “new algorithm” in [241]). Though such

data are implementation dependent, they would serve to convey a rough idea

about the behavior of the CCF algorithm. 2

Notes. The examples in this section has been computed using a sightly

modiﬁed version of the FORTRAN program originally coded by M. Ichikawa

[117] and the Mathematica program coded by M. Scharbrodt [241].

4.4.7 CCF over Rings

We consider an extension of the concept of LM-matrix and its CCF when the

ground ﬁeld is replaced by a ring. Let D be an integral domain, and K the

ﬁeld of quotients of D; it is still assumed that K is a subﬁeld of F .Tobe

more concrete, we are mainly interested in the cases where D is the ring of

integers Z or the ring of univariate polynomials over a ﬁeld.

We say that a matrix A =

is an LM-matrix with respect to (D, F ),

denoted as A ∈ LM(D, F ), if A ∈ LM(K, F ) and furthermore, Q is a matrix

over D. Accordingly, the admissible transformation over D is deﬁned to be

an invertible transformation of the form (cf. (4.35))







(4.69)

with a matrix S over D. For the invertibility of the transformation it is

imposed that S is invertible over D, i.e., that S has an inverse S

−1

over K

and furthermore each entry of S

−1

belongs to D. As is well known, matrix

S has its inverse S

−1

over D if and only if det S is an invertible element

of D, in which case S is called unimodular over D. With this terminology

we can say that an admissible transformation over D is deﬁned to be a

transformation of the form (4.69) with S unimodular over D. It is obvious

from the deﬁnition that such an admissible transformation is a transformation

in the class LM(D, F ).

Given A ∈ LM(D, F ), we can regard it as a member of LM(K, F )and

construct its CCF, say

A, using an LM-admissible transformation with a

nonsingular matrix S over K. Here we can assume that S is a matrix over D,

since we may multiply S with any nonvanishing number in D. This means

that

A ∈ LM(D, F ) (see the matrix

in Example 4.4.20 below). Note,

however, the transformation that brings A to

A is not necessarily admissible

for LM(D, F ), since S may not be unimodular over D.

The following theorem claims that, if D is a well-behaved ring called

principal ideal domain (PID), there exists an admissible transformation over

200 4. Theory and Application of Mixed Matrices

D such that the resulting matrix agrees with a CCF in its diagonal blocks.

The ring of integers Z and the ring of univariate polynomials over a ﬁeld are

typical examples of PID, where the reader is referred to van der Waerden

[325] for the deﬁnition of PID.

In the statement of the theorem below, a linear extension of a partial

order means a linear order (=total order) that is compatible with the partial

order, also called a topological sorting in computer science. Our indexing

convention (4.42) for the blocks {C

} in the CCF of A represents a linear

extension of the partial order  in the CCF.

Theorem 4.4.19. Let A be an LM-matrix with respect to (D, F ),whereD

is a PID. Let (C

; C

, ···,C

; C

∞

) denote the partition of C in the CCF of

A and  the partial order among the blocks (using the notation of Theorem

4.4.4). For any linear extension of , which is represented by the linear order

of the index k of the blocks, there exist permutation matrices P

and P

unimodular matrix S over D, and a CCF

A of A (as an LM-matrix with

respect to (K, F )) such that

A = P







is in the same block-triangular form as

A, having the same diagonal blocks,

i.e.,

A[R

]=O for k>land

A[R

] for

k =0, 1, ···,b,∞. (It is not claimed that

A[R

] coincides with

A[R

]

for k<l.)

Proof. In the proof of Theorem 4.4.4, the transformation to the Hermite nor-

mal form (see Newman [252], Schrijver [292]) under a unimodular transforma-

tion guarantees the existence of a unimodular matrix S such that

Q = SQP

satisﬁes (4.50) and (4.51). However, we cannot impose the further condition

(4.52), which fact causes the discrepancy in the upper oﬀ-diagonal blocks of

A and

Example 4.4.20. Let D = Z, K = Q,andF = Q(t

), where t

and t

are indeterminates. Consider a 3 × 3 LM-matrix with respect to (D, F )=

(Z, Q(t

)):

A =





2 −2 −4

31 2

0 t

First regard A as a member of LM(Q, Q(t

)). By choosing S = S

below

(with det S

= 1) in the LM-admissible transformation (4.35) we obtain a

CCF

, where