Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

4.4 Combinatorial Canonical Form of LM-matrices 181

Table 4.1. DM-decomposition and CCF

DM-decomposition CCF

matrix generic matrix T LM-matrix

surplus function p

= γ −|·| p = ρ + γ −|·|

rank formula

Theorem 2.2.17 (Hall–Ore): Theorem 4.2.5:

rank T =minp

+ |C| rank

=minp + |C|

transformation







4.4.4 Algorithm for CCF

We describe here an eﬃcient (polynomial time) algorithm for computing the

CCF of an LM-matrix A =

∈ LM(K, F ; m

,n). The fundamental

idea of the algorithm is to combine the following facts that have already been

established.

1. The rank of an LM-matrix is characterized by the associated LM-surplus

function p (cf. Theorem 4.2.5), and this characterization can be reformu-

lated in terms of an independent matching problem (cf. Theorem 4.2.18).

2. The CCF is constructed from L

min

(p), the family of the minimizers of

the submodular function p (cf. Theorem 4.4.4), and moreover L

min

(p)is

closely related to L

min

(κ), the family of the minimizers of the cut capacity

function κ of the associated independent matching problem (cf. Lemma

4.2.20).

3. In an independent matching problem, in general, L

min

(κ) induces a de-

composition of the vertex set (the min-cut decomposition) and moreover

the decomposition can be computed by an eﬃcient algorithm (cf. Lemma

2.3.35).

Namely, the fundamental idea of the algorithm is to compute the CCF of an

LM-matrix by ﬁnding the min-cut decomposition of the independent match-

ing problem associated with the LM-matrix.

Before going on to a detailed description of the concrete procedure, it

would be worth while demonstrating a connection between the CCF and the

DM-decomposition in the case of an LM-matrix A with Q of full-row rank.

The validity of this procedure follows from that of the general case.

Algorithm for the CCF of A with Q of full-row rank

Step 1: Find J ⊆ C such that Q[R

,J] is nonsingular and rank A = |J| +

term-rank T [R

,C\J](suchJ exists by Lemma 4.2.1 or Theorem 4.2.3).

Step 2: Put

S := Q[R

,J]

−1







A. (4.64)

182 4. Theory and Application of Mixed Matrices

Step 3: Find the DM-decomposition

A of A



, namely,

A := P



with

suitable permutation matrices P

and P

A is the CCF of A.) 2

Example 4.4.11. For the LM-matrix of Example 4.4.3, which is nonsingu-

lar, we can take J = {ξ

,ξ

,η

} in Step 1. The inverse of

Q[R

,J]=

11100

−10 0 0 0

0 −10 0 0

000−10

000−11

coincides with the transformation matrix S in Example 4.4.3. 2

The following is an algorithm for ﬁnding the CCF of a general LM-matrix.

Steps 1–3 are identical with the algorithm for computing the rank given in

§4.2.4, except that at the end of Step 2 here we go on to Step 4 for decompo-

sition. The algorithm works with the same directed graph

G =

that has vertex set

V = R

∪C

∪C and arc set

E = E

∪E

∪M

◦

where R

=Row(T ), C

= {j

| j ∈ C} is a disjoint copy of C = Col(A),

= {(i, j) | i ∈ R

,j ∈ C, T

=0},E

= {(j

,j) | j ∈ C},

and E

and M

◦

are deﬁned and updated in the algorithm; E

represents

the structure of the matroid M(Q)andM

◦

is the set of reoriented arcs in an

independent matching M ⊆ E

∪ E

. Recall also that E

and M

◦

consist

of arcs, respectively, from C

to C

and from C to R

∪ C

. The array S,

at the termination of the algorithm, gives the matrix S in the LM-admissible

transformation (4.35). When the transformation matrix is not needed, it may

simply be eliminated from the computation without any side eﬀect.

Algorithm for the CCF of an LM-matrix A

Step 1:

◦

:= ∅; base[i]:=0(i ∈ R

); P[i, j]:=Q

(i ∈ R

,j ∈ C);

S := unit matrix of order m

Step 2:

I := {i ∈ C | i

∈ ∂

−

◦

∩ C

};

J := {j ∈ C \ I |∀h : base[h]=0⇒ P [h, j]=0};

:= R

\ ∂

−

◦

; S

:= {j

∈ C

| j ∈ C \ (I ∪ J)};

:= S

∪ S

; S

−

:= C \ ∂

◦

;

:= {(i

) | h ∈ R

,j ∈ J, P [h, j] =0,i= base[h] =0};

[

E is updated accordingly]

If there exists in

G =(

E) a directed path from S

to S

−

then go to

Step 3; otherwise (including the case where S

= ∅ or S

−

= ∅)goto

Step 4.

4.4 Combinatorial Canonical Form of LM-matrices 183

Step 3:

Let L (⊆

E) be (the set of arcs on) a shortest path from S

to S

−

(“shortest” in the number of arcs);

◦

:= (M

◦

\L) ∪{(j, i) | (i, j) ∈ L ∩ E

}∪{(j, j

) | (j

,j) ∈ L ∩ E

};

If the initial vertex (∈ S

) of the path L belongs to S

, then do the

following:

{Let j

(∈ S

⊆ C

) be the initial vertex;

Find h such that base[h]=0andP [h, j] =0;

[j ∈ C corresponds to j

∈ C

]

base[h]:=j; w := 1/P [h, j];

P [k, l]:=P [k, l] − w × P [k, j] × P [h, l](k ∈ R

\{h},l ∈ C \{j});

S[k,l]:=S[k,l] − w × P [k, j] × S[h, l](k ∈ R

\{h},l ∈ R

);

P [k, j]:=0 (k ∈ R

\{h}) };

For all (i

) ∈ L ∩ E

(in the order from S

to S

−

along L)dothe

following:

{Find h such that i = base[h]; [j ∈ C corresponds to j

∈ C

]

base[h]:=j; w := 1/P [h, j];

P [k, l]:=P [k, l] − w × P [k, j] × P [h, l](k ∈ R

\{h},l ∈ C \{j});

S[k,l]:=S[k,l] − w × P [k, j] × S[h, l](k ∈ R

\{h},l ∈ R

);

P [k, j]:=0 (k ∈ R

\{h}) };

Go to Step 2.

Step 4:

Let V

∞

(⊆

V ) be the set of vertices reachable from S

by a directed

path in

Let V

(⊆

V ) be the set of vertices reachable to S

−

by a directed path

:= C ∩ V

; C

∞

:= C ∩ V

∞

;

Let



denote the graph obtained from

G by deleting the vertices V

∪V

∞

(and arcs incident thereto);

Decompose



into strongly connected components {V

| λ ∈ Λ} (V

⊆

V ), where V

 V



if and only if there is a directed path from V

to V



;

Let {C

| k =1, ···,b} be the subcollection of {C ∩V

| λ ∈ Λ} consisting

of all the nonempty sets C ∩ V

, where C

’s are indexed in such a way

that for l<kthere does not exist a directed path in



from C

to C

;

:= (R

∩ V

) ∪{h ∈ R

| base[h] ∈ C

};

∞

:= (R

∩ V

∞

) ∪{h ∈ R

| base[h] ∈ C

∞

∪{0}};

:= (R

∩ V

) ∪{h ∈ R

| base[h] ∈ C

} (k =1, ···,b);

A := P





, where the permutation matrices P

and P

are

determined so that the rows and the columns of

A are ordered as

; R

, ···,R

; R

∞

) and (C

; C

, ···,C

; C

∞

), respectively. 2

The matrix

A obtained in Step 4 is the CCF of the input matrix A, where

; R

, ···,R

; R

∞

) and (C

; C

, ···,C

; C

∞

) give the partitions of the row

set and the column set, respectively. The partial order among the blocks is

184 4. Theory and Application of Mixed Matrices

induced from the partial order among the strongly connected components

| λ ∈ Λ}. The strong component decomposition {V

| λ ∈ Λ} is es-

sentially the same as the min-cut decomposition (cf. §2.3.5) of the associated

independent matching problem, except that the partial order is reversed here.

The above algorithm runs in O(n

log n) time with arithmetic operations

in the subﬁeld K only, where m = m

+ m

=O(n) is assumed, for simplic-

ity, in this complexity bound. Note that Step 4 runs in O(n

) time, whereas

Steps 1–3 in O(n

log n) time (cf. §4.2.4). The algorithm will be eﬃcient

enough also for practical applications. It can be made more eﬃcient if we

ﬁrst compute the DM-decomposition by purely graph-theoretic algorithm

and then apply the above algorithm to each of the DM-irreducible compo-

nents; such two-stage procedure works for a nonsingular A, since the CCF

is a reﬁnement of the DM-decomposition. See Murota–Scharbrodt [241] for

improvements in implementation and Gabow and Xu [84] for a theoretical

complexity bound of (n

2.62

) for the CCF computation.

Example 4.4.12. The algorithm above is illustrated here for the 4 ×5LM-

matrix used in Examples 4.2.6, 4.2.19 and 4.2.22. After repeating Step 1 to

Step 3 (cf. Example 4.2.22) the algorithm reaches



Fig. 4.15. Graph



, V

: strongly connected components)

Step 4: V

∞

:= ∅; V

:= {x

}; C

:= {x

}; C

∞

:= ∅;

The graph



of Fig. 4.15 is obtained;

Strongly connected components of



are given by {V

}, where

= {x

}, V

= {x

} and V

 V

;

Since C ∩ V

= ∅,wehaveb := 1 and C

:= C ∩ V

= {x

};

:= {r

}; R

∞

:= ∅; R

:= {r

};

4.4 Combinatorial Canonical Form of LM-matrices 185

A := P





11020

1 −10

0 t

is the CCF. 2

Example 4.4.13. This is an example with a nonempty vertical tail. Con-

sider

A =





100101−1

−20 1−20 0 2

100111−1

where T = {t

| i =1, ···, 13} is the set of algebraically independent pa-

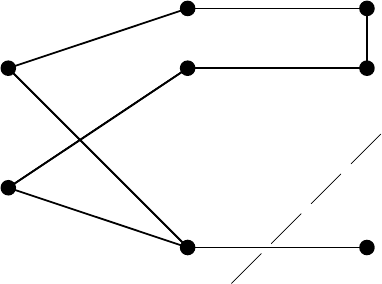
rameters. The bipartite graph G =(V

−

; E) with V

= R

∪ C

−

= C for the independent matching problem is depicted in Fig. 4.16, where

= {f

, ···,f

}, C = {x

, ···,x

} and C

= {x

, ···,x

}. A maximum

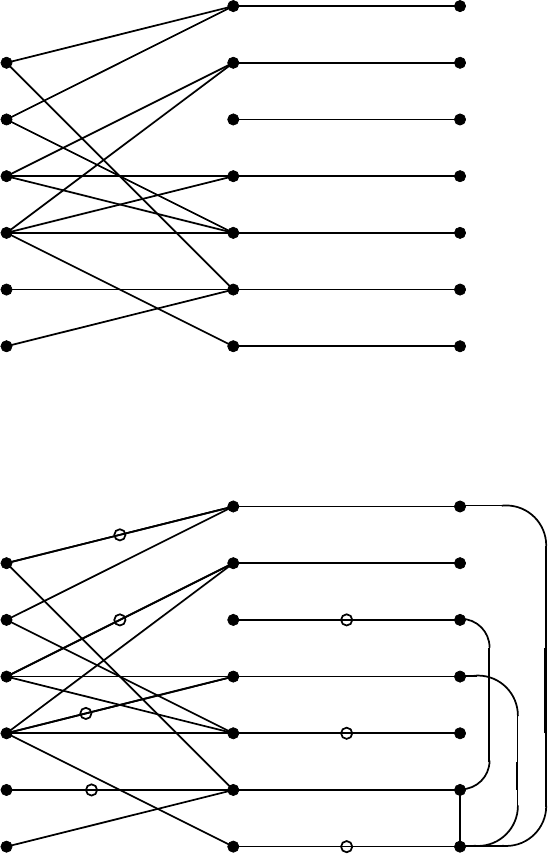
independent matching M of size 7 is found. The auxiliary graph

G is shown

in Fig. 4.17, from which we obtain the partition {V

; V

, ···,V

; V

∞

} of

V = R

∪ C

∪ C, where

= ∅,V

∞

= {f

= {x

},V

= {f

},V

= {x

}

= {x

},V

= {x

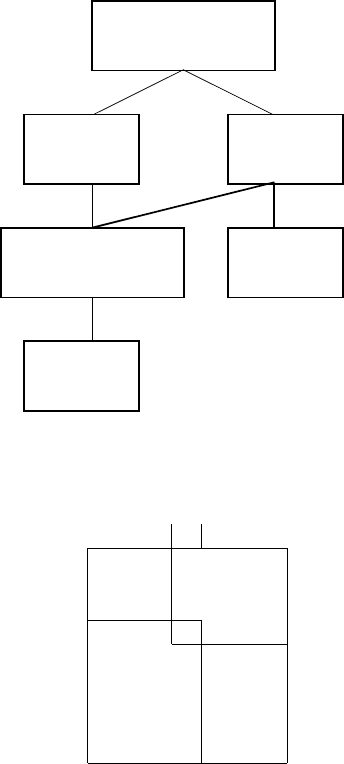
with the partial order shown in Fig. 4.18. For the partition of the column set

we have (C

; C

∞

) with

= ∅,C

= C ∩ V

= {x

},C

= C ∩ V

= {x

∞

= C ∩ V

∞

= {x

Notice that C

and C

have no order relation with each other. The CCF of

A is given by

186 4. Theory and Application of Mixed Matrices



Fig. 4.16. Independent matching problem of Example 4.4.13







Fig. 4.17. Auxiliary graph

G of Example 4.4.13 (: arc in a maximum inde-

pendent matching M;+:vertexinS

; S

−

= ∅)

4.4 Combinatorial Canonical Form of LM-matrices 187

∞

Fig. 4.18. Partial order of Example 4.4.13 (V

= ∅)

A =

∞

01−1 11

0 t

1 2

010

0 t

00t

4.4.5 Decomposition of Systems of Equations by CCF

When solving a system of linear equations Ax = b repeatedly for right-hand

side vectors b = b(θ) with varying parameters θ but with a ﬁxed coeﬃcient

matrix A, it is standard to ﬁrst decompose A (possibly with permutations of

rows and columns) into LU-factors as A = LU , and then solve the triangular

systems Ly = b, Ux = y for diﬀerent values of b = b(θ). It is important here

that the LU-factors of A can be determined independently of the parameters

θ.

No less of interest are the cases where the coeﬃcient A, as well as b,

changes with parameters, but with its zero/nonzero pattern kept ﬁxed. Such

188 4. Theory and Application of Mixed Matrices

situations often arise in practice, for example, in solving a system of non-

linear equations by the Newton method, or in determining the frequency

characteristic of an electrical network by computing its responses to inputs

of various frequencies. In this case we cannot calculate the LU-factors of A

in advance, so that we usually resort to graph-theoretic methods and rear-

range the equations and the variables to obtain a block-triangular form. In

particular, the block-triangularization based on the DM-decomposition is of

fundamental importance. Each time the parameter values are speciﬁed, the

equations corresponding to the DM-blocks may be solved either by direct

inversion through LU-decomposition or by some iterative method.

The above two approaches, namely, the LU-decomposition and the DM-

decomposition, are two extremes in that the former applies to a constant

matrix A with ﬁxed numerical values and the latter to a symbolic matrix

A with a ﬁxed pattern. It is often the case, however, that the matrix A is a

mixture of constant numbers and symbols, which may be modeled as a mixed

matrix under the assumption of algebraic independence of the symbols.

As a typical situation, let us consider the iterative solution of a system of

linear/nonlinear equations f(x)=0 by the Newton method. This amounts to

solving J(x)Δx = −f(x) for a correction Δx through the LU-decomposition

of J(x), where J(x) is the Jacobian matrix of f(x). The equations may be

divided into linear and nonlinear parts as f(x)=Qx + g(x), where Q is

a constant matrix. Accordingly, we have J(x)=Q + T (x), where T (x)is

the Jacobian matrix of the nonlinear part g(x). Then we may treat J(x)=

Q+

T (x) as a mixed matrix, regarding (or modeling) the nonvanishing entries

of T (x) as independent symbols, even when the nonvanishing entries of T (x)

are subject to algebraic relations.

We will describe here how the CCF can be utilized to generate an eﬃcient

solution of a system of equations

A(θ)x = b(θ) (4.65)

for varying values of parameters θ, where x, b ∈ R

. We express the coeﬃcient

matrix as

A(θ)=Q + T (θ)

and regard it as a mixed matrix with ground ﬁeld Q or R treating the

nonvanishing entries of T (θ) as if they were algebraically independent. As

discussed in §4.1, we may introduce an auxiliary vector w to obtain the

augmented system of equations with the LM-matrix

A of (4.4) or (4.6) as the

coeﬃcient matrix (where we may put t

= 1 for all i).

The CCF of

A, being a block-triangular matrix, determines a hierarchical

decomposition of the whole augmented system into smaller subsystems. Since

the LM-admissible transformation (4.35) is more general than permutations,

the problem decomposition by the CCF is ﬁner than the one by the DM-

decomposition. The crucial point is that the transformation (4.35) needed in

the CCF decomposition is determined independently of the particular values

4.4 Combinatorial Canonical Form of LM-matrices 189

of θ and hence this procedure is feasible in practice. That is, we can use one

and the same decomposition for varying values of θ and then we may repeat-

edly solve the subproblems with the diagonal CCF-blocks as the coeﬃcients

whenever the parameter values are speciﬁed.

For the subproblems to be solved uniquely, the diagonal blocks of the CCF

A must be nonsingular. If the assumption of the algebraic independence

of the nonvanishing entries of T(θ) is literally met, the nonsingularity of the

diagonal blocks is guaranteed by Theorem 4.4.4. Even if the assumption is not

satisﬁed, the diagonal blocks must be nonsingular if the original coeﬃcient

matrix A is nonsingular at all, which fact is obvious from the block-triangular

structure of the matrix. Therefore the decomposition procedure above can be

carried out successfully if the original system is uniquely solvable at all.

Let

be the kth diagonal block of the CCF of

A in (4.4) (with t

= 1),

which is the coeﬃcient matrix of the kth subproblem. The row set of

divided into R

and R

. The column set, say C

, is also partitioned as

= C

∪ C

, where C

and C

correspond to part of the variables w

and x, respectively. In what follows we show that

min(|C

|, |R

|) (4.66)

can be adopted as a rough measure for the substantial size of the subproblem.

The kth subproblem may be solved as follows. Since

is LM-irreducible,

the T -part of

does not have zero columns. Hence the subproblem can be

expressed as

⎛

⎝

−IT

↓ OT

⎞

⎠





⎛

⎝

⎞

⎠

where

(θ) is to be computed from b(θ) each time θ is given. On

eliminating the auxiliary variable w

we obtain a system of equations



+ Q







in |C

| variables. The amount of computation needed to determine x

this way may be estimated roughly by

||C

| + |C

Another approach to the subproblem may be conceivable that makes no

distinction between w

and x

. Since

] is of full-row rank, we can

make the subsystem into the form











(4.67)

190 4. Theory and Application of Mixed Matrices

by a nonsingular transformation independent of θ, where (z

, z

)isarear-

rangement of (w

, x

). The Gaussian elimination procedure applied to (4.67),

possibly with permutations of rows in R

, can be done with

| + |R

arithmetic operations.

In practical applications, the following procedure would be recommended

for the solution of (4.65).

[Problem decomposition by the CCF]

1. Introduce auxiliary variables to separate the equations that depend on

the parameters. Denote by

A the coeﬃcient matrix of the augmented

system, which is now in the form:

A =



T (θ)



To be more precise, express the ith equation of (4.65) as



j∈J



j∈K

(θ)x

= b

(θ).

In case |J

|≥1and|K

|≥1, we introduce an auxiliary variable, say w

to obtain



j∈J

+ w

= b

(θ),



j∈K

(θ)x

− w

=0.

Denoting by m

the number of auxiliary variables thus introduced, we

see that m

≤ n and

A is an (m

+ n) × (m

+ n) matrix.

2. Find the DM-decomposition of

A into blocks (

| 1 ≤ k, l ≤ D)to

obtain the block-triangularization:

⎛

⎜

⎝

···

OO··· O

⎞

⎟

⎠

⎛

⎜

⎝

⎞

⎟

⎠

⎛

⎜

⎝

(θ)

⎞

⎟

⎠

where z =(z

, ···, z

) is a rearrangement of the variables (x, w).