Murota K. Matrices and Matroids for Systems Analysis
Подождите немного. Документ загружается.

4.3 Structural Solvability of Systems of Equations 161
is structurally solvable under GA2 if and only if M = N and the maximum
size of a common independent set of M([I
M+K
| Q])
∗
and M([I
M+K
| T ]) is
equal to N + K.
Proof. Apply the rank formula of Theorem 4.2.10 to A = Q + T , which is a
mixed matrix under GA2.
Theorem 4.3.7 implies that we can test for the structural solvability under
GA2 by the efficient matroid-theoretic algorithm of §4.2.4 using arithmetic
operations on rational numbers. It is important in practice that the entries
of Q are often simple integers and it seems, empirically, that no serious nu-
merical difficulty arises from the round-off errors in handling those “rational”
numbers.
Example 4.3.8. By way of the hypothetical ethylene dichloride production
system described in Example 3.1.3, we will demonstrate the effectiveness of
Theorem 4.3.7 as compared to the graph-theoretic criterion (Theorem 4.3.2)
for the structural solvability under the assumption GA1.
x
y
u
u
71
u
72
u
51
u
52
u
53
u
61
u
62
u
63
u
31
u
32
u
33
u
41
u
42
u
43
*
^
^
^
-
-
-
-
-
U
-
?
?
?
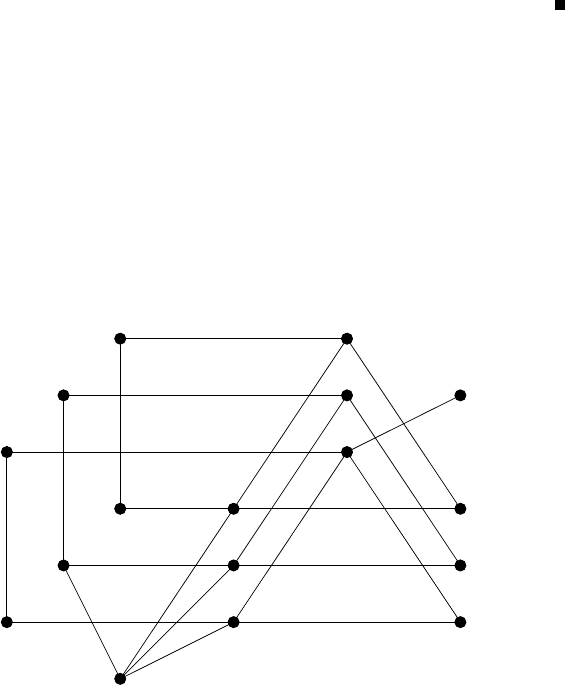
Fig. 4.10. Representation graph of the system (3.5) (cf. Example 3.1.3)
The system (3.5) of equations is in the form (4.27) with M = N =1
and K = 15. The representation graph of this system, as defined in §4.3.2,
is depicted in Fig. 4.10, on which a Menger-type perfect linking (e.g., x →
u
63
→ y)existsfromthex-vertex {x} to the y-vertex {y}. Therefore the
graph-theoretic method (Theorem 4.3.2), assuming GA1, would conclude that
this system was structurally solvable, in contradiction to the fact that the
Jacobian of this system (Fig. 3.4) vanishes for any value of a
1
, a
2
, r, x,and
u
53
.
162 4. Theory and Application of Mixed Matrices
This contradiction stems from the assumption GA1, which obviously fails
to hold in this case. In fact, in the DM-decomposition of the Jacobian matrix,
shown in Fig. 4.11, we can detect the rank deficiency in the 4 × 4block
corresponding to variables {u
43
,u
33
,u
63
,u
53
}. A more adequate assumption
for this problem would be the GA2, which implies the choice of K = Q and
T = {a
1
,a
2
,r,x,u
53
}.
u
71
u
61
u
51
u
41
u
31
xu
43
u
33
u
63
u
53
u
72
uu
62
u
52
u
42
u
32
u
71
−1 −11
u
61
−1 a
1
00
u
51
0 −110 −1
u
41
00−11
u
31
100−1
u
63
u
53
−1 x
u
53
100−1 1
u
43
−1100
u
33
0 −110
y 00−11
u
72
−1 −11
u −100r 0
u
62
0 −1 a
2
00
u
52
−10−110
u
42
000−11
u
32
0100−1
Fig. 4.11. DM-decomposition of the Jacobian matrix of (3.5) (cf. Fig. 3.4)
Accordingly, the Jacobian matrix, say A, of Fig. 3.4 is recognized as a
mixed matrix with respect to Q, to which the algorithm of §4.2.4 is applied.
The maximum size of a common independent set of M([I | Q])
∗
and M([I |
T ]) is equal to 15, whereas N + K = 16. Theorem 4.3.7 then reveals that the
system (3.5) is not structurally solvable.
Alternatively, we may consider the LM-matrix (4.6) associated with A,
which is given in Fig. 4.12. Since A contains four mixed rows, namely, the rows
indexed by u
61
, u
62
, u
63
and u, it suffices to increase the size of the matrix
by four. As a result the associated LM-matrix is 20 ×20. An implementation
of the algorithm of §4.2.4 found the rank to be 19, with deficiency 1. Hence
the system (3.5) is not structurally solvable. 2
Example 4.3.9. Recall the electrical network of Example 3.1.2 containing
mutual couplings. If we regard the set of the physical parameters {r
1
,r
2
,α,β}
as being algebraically independent over Q, assuming GA2, the coefficient
matrix, say A, of (3.3) is a mixed matrix with respect to (Q, F )forF =
Q(r
1
,r
2
,α,β), i.e., A ∈ MM(Q, F , 10, 10). It is expressed as A = Q + T
with

4.3 Structural Solvability of Systems of Equations 163
w
1
w
2
w
3
w
4
xu
31
u
32
u
33
u
41
u
42
u
43
u
51
u
52
u
53
u
61
u
62
u
63
u
71
u
72
u
u
61
1 −1
u
62
1 −1
u
63
1 −1
u 1 −1
y 1 −1
u
31
−11
u
32
−11
u
33
−11
u
41
1 −1
u
42
1 −1
u
43
1 −1
u
51
1 −1 −1
u
52
1 −1 −1
u
53
1 −11
u
71
1 −1 −1
u
72
1 −1 −1
u
61
−t
1
a
1
u
62
−t
2
a
2
u
63
−t
3
u
53
x
u −t
4
r
Fig. 4.12. LM-matrix associated with Jacobian matrix of (3.5) (chemical process
simulation in Example 3.1.3)
Q =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
00111
1000−1
01−100
100−11
011−10
0 −1
0 −1
0 −1
−10
0 −1
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
T =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
00000
00000
00000
00000
00000
r
1
0
r
2
0
0 α 0
β 00
00
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
164 4. Theory and Application of Mixed Matrices
Then we can apply Theorem 4.2.10 to check for the solvability of this electrical
network.
Or alternatively, we may treat A as if it were a layered mixed matrix,
A ∈ LM(Q, F ;5, 5, 10), as follows. On expressing A as
A =
Q
T
with
Q =
⎡
⎢
⎢
⎢
⎢
⎣
00111
1000−1
01−100
100−11
011−10
⎤
⎥
⎥
⎥
⎥
⎦
,
T =
⎡
⎢
⎢
⎢
⎢
⎣
r
1
−1
r
2
−1
0 α −1
β −10
0 −1
⎤
⎥
⎥
⎥
⎥
⎦
and conceptually multiplying the rows of T by algebraically independent
transcendentals, we can apply Theorem 4.2.2 or Theorem 4.2.3. We may take
J = {ξ
3
,ξ
4
,ξ
5
,η
3
,η
4
} for the subset that attains the maximum (=10) on the
right-hand side of (4.12). Therefore A is nonsingular.
The latter approach agrees with the established method for testing the
unique solvability of an electrical network (Iri [127, 128], Iri–Tomizawa [131,
132], Petersen [267], Recski [275, 276, 277]). It is remarkable in the case of an
electrical network that the matrix Q above, expressing the incidence relations
in the underlying graph, is totally unimodular over Z, and hence totally free
from rounding errors in the pivoting operations. 2
The structural solvability of two realistic problems in chemical engineering
is investigated below by the matroid-theoretic method under the realistic
assumption GA2.
Example 4.3.10 (Reactor-separator model). This example is taken
from the reactor-separator model (EV-6) of Yajima–Tsunekawa–Kobayashi
[344]. The original problem, involving 218 variables, is modified to the stan-
dard form (4.27) with 120 unknowns and as many equations; N = M =18
and K = 102 in the notation of (4.27). The Jacobian matrix in Fig. 4.13 is
sparse, containing 351 nonvanishing entries.
Before the matroid-theoretic method is considered, it is confirmed by
the graph-theoretic method (by Theorem 4.3.2) that the whole system of
equations is structurally solvable under the generality assumption GA1.
Of the 351 nonvanishing entries of the Jacobian matrix of size 120, 172
entries are rational constants (1 or −1) and the remaining 179 entries are
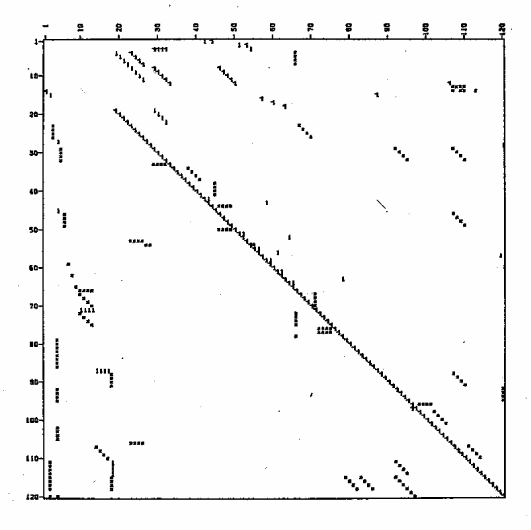
4.3 Structural Solvability of Systems of Equations 165
Fig. 4.13. Jacobian matrix of the reactor-separator model (Example 4.3.10)
regarded here as being algebraically independent, by assuming GA2. Ac-
cordingly, the Jacobian matrix A belongs to MM(Q, F ; 120, 120). Then the
maximum size of a common independent set I ∪J (I ⊆ Row(A),J ⊆ Col(A))
of M([I
120
| Q])
∗
and M([I
120
| T ]) is found to be 120 with |I| =91and
|J| = 29. Therefore this system of equations remains to be structurally solv-
able under the more realistic assumption GA2.
In passing we mention the M- and L-decompositions (cf. Remark 4.3.5).
This system is decomposed by the M-decomposition into 71 structurally solv-
able subproblems, of which only four components have more than one un-
known variable; more precisely, the four components have 25, 10, 9 and 9
unknowns, respectively. The L-decomposition, on the other hand, leads to 47
structurally solvable subproblems, the largest being of size 48. See Murota
[204, §11] for detailed data about these decompositions. 2
Example 4.3.11 (Hydrogen production system). This example arises
from an analysis of an industrial hydrogen production system. The standard
form (4.27) of equations with N = M =13andK = 531 is obtained; it
involves N + K = 544 unknowns and as many equations. Fig. 4.14 demon-

166 4. Theory and Application of Mixed Matrices
strates the sparsity of the Jacobian matrix A, which has 1464 nonvanishing
entries.
Fig. 4.14. Jacobian matrix of the hydrogen production system (Example 4.3.11)
The whole system is structurally solvable under GA1, as verified by the
graph-theoretic method of Theorem 4.3.2.
Under the generality assumption GA2, the 1464 nonvanishing entries of
the Jacobian matrix A are divided into 1142 rational constants (1 or −1) and
322 algebraically independent transcendentals. For a common independent
set I ∪ J (I ⊆ Row(A),J ⊆ Col(A)) of M([I
544
| Q])
∗
and M([I
544
| T ])
such that |J| is maximal, we have |I| = 455 and |J| = 89. It is noteworthy
that the maximum size of J is much smaller than term-rank T = 178. It
may also be remarked that no fractions are involved in the course of pivotal
transformations of Q-matrix, although Q has not been proved to be totally
unimodular.
We mention again the M- and L-decompositions (cf. Remark 4.3.5). The
M-decomposition yields 268 structurally solvable subproblems, while the L-
decomposition 234 subproblems. The size of an M-component varies from 1 to
104, whereas that of an L-component from 1 to 120. There is no substantial
4.4 Combinatorial Canonical Form of LM-matrices 167
difference between the two decompositions in this example. See Murota [204,
§11] for detailed data about these decompositions. 2
We will return to the above problems in §4.4.6 to illustrate the application
of a matroid-theoretic decomposition technique for systems of equations.
Notes. In Examples 4.3.8, 4.3.10, and 4.3.11, the problem data was provided
by J. Tsunekawa and S. Kobayashi of the Institute of Japanese Union of
Scientists and Engineers and the computation was done by M. Ichikawa [117].
4.4 Combinatorial Canonical Form of LM-matrices
4.4.1 LM-equivalence
For an LM-matrix A =
.
Q
T
/
∈ LM(K, F ; m
Q
,m
T
,n) we define an LM-
admissible transformation to be a transformation of the form:
P
r
SO
OI
Q
T
P
c
, (4.35)
where P
r
and P
c
are permutation matrices, and S is a nonsingular matrix over
the ground field K (i.e., S ∈ GL(m
Q
, K)). An LM-admissible transformation
brings an LM-matrix into another LM-matrix, since
SO
OI
Q
T
=
SQ
T
and SQ is again a matrix over K. Two LM-matrices are said to be LM-
equivalent if they are connected by an LM-admissible transformation. If A
is LM-equivalent to A, then Col(A
) may be identified with Col(A) through
the permutation P
c
.
The objective of this section is to consider a block-triangular decomposi-
tion of LM-matrices under the LM-admissible transformation (4.35). It will be
shown that there exists a canonical proper block-triangular form (“proper”
in the sense of §2.1.4) among the matrices LM-equivalent to a given LM-
matrix. The canonical form is called the combinatorial canonical form or
CCF for short.
In the special case where m
Q
= 0, the LM-admissible transforma-
tion (4.35) reduces to P
r
TP
c
, involving permutations only. Accordingly the
decomposition by means of the LM-admissible transformation reduces to
the Dulmage–Mendelsohn decomposition. In the other extreme case where
m
T
= 0, the transformation (4.35) reduces to P
r
SQP
c
, and the decomposi-
tion by means of (4.35) agrees with the ordinary Gauss–Jordan elimination in
matrix computation. Hence, the theory of CCF to be developed here amounts
to a natural amalgamation of the results on the DM-decomposition and the
LU-decomposition.
Example 4.4.1. Consider a 3 × 3 LM-matrix
168 4. Theory and Application of Mixed Matrices
A =
Q
T
=
⎛
⎝
11 0
12 3
0 t
1
t
2
⎞
⎠
,
where T = {t
1
,t
2
} is the set of algebraically independent parameters. This
matrix cannot be decomposed into smaller blocks by means of permutations
of rows and columns (DM-irreducible). However, by choosing S =
10
−11
and P
r
= P
c
= I in the LM-admissible transformation (4.35), we can obtain
a block-triangular decomposition:
¯
A =
SQ
T
=
⎛
⎝
1
10
13
t
1
t
2
⎞
⎠
.
Thus the LM-admissible transformation is more powerful than mere permu-
tations. 2
Example 4.4.2. Here is an example containing a “tail” (nonsquare diagonal
block as in the DM-decomposition). Recall the 4 × 5 LM-matrix
A =
Q
T
=
x
1
x
2
x
3
x
4
x
5
11110
02110
f
1
t
1
000t
2
f
2
0 t
3
00t
4
used in Examples 4.2.19 and 4.2.22. By choosing
S =
1 −1
01
,P
r
=
⎡
⎢
⎢
⎣
0100
1000
0010
0001
⎤
⎥
⎥
⎦
,P
c
=
⎡
⎢
⎢
⎢
⎢
⎣
00100
00010
10000
01000
00001
⎤
⎥
⎥
⎥
⎥
⎦
in the LM-admissible transformation (4.35), we obtain the CCF:
¯
A =
x
3
x
4
x
1
x
2
x
5
11020
1 −10
f
1
t
1
0 t
2
f
2
0 t
3
t
4
with a nonempty horizontal tail C
0
= {x
3
,x
4
}, a single square block C
1
=
{x
1
,x
2
,x
5
}, and an empty vertical tail C
∞
= ∅. Note the rank deficiency is
localized to the tail, and accordingly, this is a proper block-triangularization
in the sense of §2.1.4. 2

4.4 Combinatorial Canonical Form of LM-matrices 169
Example 4.4.3. Let us discuss a physical meaning of the LM-equivalence
with reference to the electrical network of Example 3.1.2. Consider an LM-
matrix
A =
Q
T
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
ξ
1
ξ
2
ξ
3
ξ
4
ξ
5
η
1
η
2
η
3
η
4
η
5
00 1 1 1 000 0 0
10 0 0−1000 0 0
01−10 0 000 0 0
00 0 0 0 100−11
00 0 0 0 011−10
r
1
0000t
1
00 0 0
0 r
2
0000t
2
000
00 0 0 0α 0 t
3
00
0 β 0 t
4
0 000 0 0
00 0 0 0 000 0t
5
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
,
where T = {r
1
,r
2
,α,β; t
1
, ···,t
5
} is the set of algebraically independent
parameters. This matrix is essentially the same as the coefficient matrix of
(3.3).
A block-triangular form under the LM-admissible transformation (4.35)
is obtained as follows. Choosing
S =
⎛
⎜
⎜
⎜
⎝
0 −10 00
00−100
11100
00 0−10
00 0−11
⎞
⎟
⎟
⎟
⎠
in (4.35) we first transform Q to
Q
= SQ =
⎛
⎜
⎜
⎜
⎜
⎝
ξ
1
ξ
2
ξ
3
ξ
4
ξ
5
η
1
η
2
η
3
η
4
η
5
−10 001 0 000 0
0 −1100 0 000 0
1 1 010 0 000 0
00000−1001−1
00000−1110−1
⎞
⎟
⎟
⎟
⎟
⎠
, (4.36)
and then permute the rows and the columns of
Q
T
with permutation
matrices P
r
and P
c
defined respectively by
170 4. Theory and Application of Mixed Matrices
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
0100000000
1000000000
0001000000
0010000000
0000100000
0000010000
0000001000
0000000100
0000000010
0000000001
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
,
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
0001000000
0000100000
1000000000
0000010000
0100000000
0000001000
0000000100
0000000010
0010000000
0000000001
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
to obtain an explicit block-triangular LM-matrix
¯
A = P
r
Q
T
P
c
=
ξ
3
ξ
5
η
4
ξ
1
ξ
2
ξ
4
η
1
η
2
η
3
η
5
1 −1
1 −1
1 −1 −1
1 11000
000−11 1−1
r
1
00t
1
00
0 r
2
00t
2
0
000α 0 t
3
0 βt
4
000
t
5
.
It turns out that this is the finest block-triangular matrix which is LM-
equivalent to A. Namely,
¯
A is the CCF of A.
The column set of
¯
A is partitioned into five blocks:
C
1
= {ξ
3
},C
2
= {ξ
5
},C
3
= {η
4
},C
4
= {ξ
1
,ξ
2
,ξ
4
,η
1
,η
2
,η
3
},C
5
= {η
5
}.
A partial order among the blocks:
C
5
↑
C
4
#↑$
C
1
C
2
C
3
(4.37)
is defined by the zero/nonzero structure of
¯
A. This partial order indicates,
for example, that the blocks C
1
and C
2
, having no order relation, could be
exchanged in position without destroying the block-triangular form provided
the corresponding rows are exchanged in position accordingly. This corre-
sponds to the fact that the entry in the first row of the column ξ
5
is equal to
0.
The matrix Q has been obtained from the Kirchhoff’s conservation laws.
In Example 3.1.3 we have chosen three nodes a, b, c in Fig. 3.2 for the KCL
(Kirchhoff’s current law) to obtain
