Murota K. Matrices and Matroids for Systems Analysis
Подождите немного. Документ загружается.


4.2 Rank of Mixed Matrices 141
Theorem 4.2.13 (K¨onig–Egerv´ary theorem for mixed matrix). Let
A = Q + T be a mixed matrix. Then there exist I ⊆ R and J ⊆ C such that
(i) |I|+ |J|−rank Q[I,J]=|R| + |C|−rank A,
(ii) rank T [I,J]=0.
Proof.Take(I,J) that attains the minimum on the right-hand side of (4.23).
Remark 4.2.14. Theorem 4.2.13 is a refinement of the previous result of
Hartfiel–Loewy [102] for a square mixed matrix, named the “determinan-
tal version of the Frobenius–K¨onig theorem,” and its extension to a general
rectangular mixed matrix by Murota [218]. The original proof of Hartfiel–
Loewy (for the square case) was quite involved, based on factorizations of
determinants. 2
Remark 4.2.15. As is naturally expected, the K¨onig–Egerv´ary-type result
(Theorem 4.2.13) is equivalent to the rank formula (4.23), under an obvious
inequality
rank A ≤ rank A[R, J]+rankA[R, C \ J]
≤ rank A[I,J]+rankA[R \ I,J]+rankA[R, C \J]
≤ rank Q[I,J]+|R \ I|+ |C \ J|
valid for (I,J) with T [I,J]=O (i.e., with I ∩
ˆ
Γ (R, J)=∅).
Furthermore, it is pointed out by Bapat [9] that Theorem 4.2.13 can be
proved independently of the rank formula using a fundamental property of a
general bimatroid. By Theorem 2.3.47 (applied to the bimatroid associated
with A), there exist I ⊆ R and J ⊆ C such that
(i) |I| + |J
|−rank A[I,J]=|R| + |C|−rank A,
(ii) rank A[I \{i},J \{j}]=rankA[I,J], ∀i ∈ I, ∀j ∈ J.
We claim that (ii) implies T [I,J]=O. Suppose, to the contrary, that T
ij
=0
for some i ∈ I and j ∈ J. Since rank A[I \{i},J \{j}]=rankA[I,J](=:r),
there exist I
⊆ I \{i} and J
⊆ J \{j} such that rank A[I
,J
]=|I
| =
|J
| = r. Consider the Laplace expansion of det A[I
∪{i},J
∪{j}]. It contains
a nonvanishing term T
ij
· det A[I
,J
], which is not cancelled out by virtue
of the algebraic independence of the nonzero entries of T . This implies a
contradiction that r =rankA[I,J] ≥ rank A[I
∪{i},J
∪{j}]=|I
| +1=
r +1. 2
Remark 4.2.16. When numerical values are substituted into the nonzero
entries of the T -part of a mixed matrix, the rank of the resulting numerical
matrix can possibly decrease. On the basis of Theorem 4.2.13 a systematic
procedure has been given by Geelen [92] that assigns numerical values so that
the rank remains the same. 2
Finally we mention the following fact in connection with the basic rank
identity (4.20).

142 4. Theory and Application of Mixed Matrices
Theorem 4.2.17. For a maximizer (I,J) in (4.20) that is minimal with
respect to set inclusion, we have |I| = |J| and det A[I,J] ∈ K
∗
,whereK
∗
=
K \{0}.
Proof. Suppose |I| > rank Q[I,J]. Then there exists i ∈ I such that
rank Q[I,J]=rankQ[I \{i},J]. This implies that (I \{i},J) is also a maxi-
mizer in (4.20), which contradicts the minimality of (I,J). Similarly for |J|.
Hence |I| = |J| =rankQ[I,J], that is, Q[I,J] is nonsingular, and a fortiori
A[I,J] is nonsingular, i.e., det A[I,J] =0.
Suppose det A[I,J] ∈ K. Then there exist nonempty I
⊆ I and
nonempty J
⊆ J such that both T [I
,J
]andQ[I \ I
,J \ J
] are non-
singular, which implies that (I \ I
,J \ J
) is also a maximizer in (4.20), a
contradiction.
A mixed matrix A with the property det A ∈ K
∗
will be investigated in
§4.6.1.
Notes. The rank formulas for mixed matrices (Lemma 4.2.7, Theorem 4.2.8,
Theorem 4.2.9, Theorem 4.2.10) are due to Murota–Iri [237, 238]. Theorem
4.2.17 is by Murota [198].
4.2.3 Reduction to Independent Matching Problems
We explain how the computation of rank A for an LM-matrix A =
.
Q
T
/
can
be reduced to solving an independent matching problem. This leads to an
efficient algorithm, to be described in §4.2.4, for computing the rank of an
LM-matrix with arithmetic operations in the ground field K.
Here and henceforth C
Q
= {j
Q
| j ∈ C} denotes a disjoint copy of
C = Col(A) (with j
Q
∈ C
Q
denoting the copy of j ∈ C), whereas R
Q
=
Row(Q), R
T
=Row(T ), |R
Q
| = m
Q
, |R
T
| = m
T
and |C| = n. Denote by
M(Q)=(C
Q
, I
Q
) the matroid associated with Q, where C
Q
= Col(Q)and
I
Q
is the family of independent sets, namely,
I
Q
= {J
Q
⊆ C
Q
| rank Q[R
Q
,J
Q
]=|J
Q
|}.
We consider an independent matching problem defined on a bipartite
graph G =(V
+
,V
−
; E) with V
+
= R
T
∪ C
Q
, V
−
= C and E = E
T
∪ E
Q
,
where
E
T
= {(i, j) | i ∈ R
T
,j ∈ C, T
ij
=0},E
Q
= {(j
Q
,j) | j ∈ C}.
The matroid M
+
=(V
+
, I
+
) attached to V
+
is the direct sum of the free
matroid on R
T
and M(Q)onC
Q
, i.e.,
I
+
= {I
+
⊆ V
+
| I
+
∩ C
Q
∈I
Q
},
whereas the free matroid M
−
=(V
−
, I
−
) (with I
−
=2
V
−
) is attached to
V
−
. The set of the end-vertices of a matching M will be designated as ∂M
(⊆ V ).
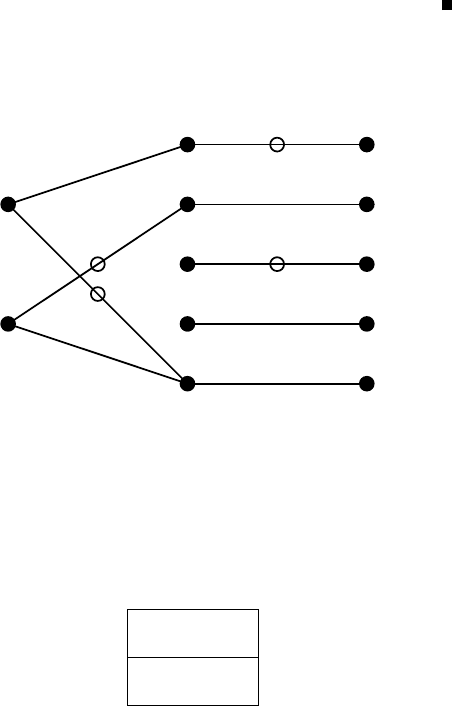
4.2 Rank of Mixed Matrices 143
We then have the following characterization of rank A in terms of the
maximum size of an independent matching.
Theorem 4.2.18. For an LM-matrix A, rank A coincides with the maximum
size of an independent matching in the independent matching problem defined
above. That is,
rank A = max{|M||M: independent matching}.
Proof. The proof is based on the basic rank identity of Theorem 4.2.2. Con-
sider J ⊆ C that attains the maximum on the right-hand side of (4.12).
We may assume that rank Q[R
Q
,J]=|J|. Then there exists an independent
matching M such that ∂M ∩C
Q
= J
Q
and |∂M ∩R
T
| = term-rank T [R
T
,C\
J], where J
Q
⊆ C
Q
is the copy of J. Hence follows rank A ≤|M|. Con-
versely, given an independent matching M, we put J
Q
= ∂M ∩C
Q
to obtain
rank Q[R
Q
,J]=|J| and term-rank T [R
T
,C \ J] ≥|∂M ∩ R
T
|. This shows
rank A ≥ rank Q[R
Q
,J] + term-rank T [R
T
,C \ J] ≥|M |.
R
T
CC
Q
E
T
E
Q
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
1
R
3
q
Fig. 4.1. Graph G (: arc in a maximum independent matching M)
Example 4.2.19. The independent matching problem associated with the
4 × 5 LM-matrix in Example 4.2.6:
A =
Q
T
=
x
1
x
2
x
3
x
4
x
5
11110
02110
f
1
t
1
000t
2
f
2
0 t
3
00t
4
144 4. Theory and Application of Mixed Matrices
is illustrated in Fig. 4.1. The columns and the rows are indexed as Col(A)=
C = {x
1
,x
2
,x
3
,x
4
,x
5
} and Row(T )=R
T
= {f
1
,f
2
} and accordingly
C
Q
= {x
1Q
,x
2Q
,x
3Q
,x
4Q
,x
5Q
}. A maximum independent matching M =
{(f
1
,x
5
), (f
2
,x
2
), (x
1Q
,x
1
), (x
3Q
,x
3
)} is marked by !.WehaverankA =
|M| = 4. Note also that J = {x
1
,x
3
}, corresponding to J
Q
= ∂M ∩ C
Q
=
{x
1Q
,x
3Q
}, attains the maximum on the right-hand side of (4.12). 2
The LM-surplus function p characterizing the rank of A in the identity
(4.19) of Theorem 4.2.5 is closely related to the cut function of the indepen-
dent matching problem. The rank functions ρ
+
and ρ
−
of M
+
and M
−
are
given by
ρ
+
(X)=|X ∩ R
T
| + ρ(X ∩ C
Q
),X⊆ V
+
,
ρ
−
(Y )=|Y |,Y⊆ V
−
.
For U ⊆ V
+
∪ V
−
, there is no arc going out of U if and only if Γ (J) ⊆ I
and J ⊆ K, where I = R
T
\ U , J = C \ U,andK (⊆ C) is the copy of
K
Q
= C
Q
\ U (⊆ C
Q
). Then the cut function κ(U) (cf. (2.71)) is given by
κ(U)=ρ
+
(V
+
\ U )+ρ
−
(V
−
∩ U )=|I|+ ρ(K)+|C \ J|, (4.25)
and its minimum can be computed as follows:
min
U
{κ(U) | U ⊆ V
+
∪ V
−
}
= min
I,J,K
{|I| + ρ(K)+|C \ J||Γ (J) ⊆ I,J ⊆ K}
= min
J
{|Γ (J)|+ ρ(J)+|C \ J||J ⊆ C}
= min
J
{γ(J)+ρ(J) −|J||J ⊆ C} + |C|
= min
J
{p(J) | J ⊆ C}+ |C|. (4.26)
This reveals the following relation between the minimizers of p and κ.
Lemma 4.2.20.
L
min
(p)={J ⊆ C | J = C \U, U ∈L
min
(κ)},
where L
min
(p) and L
min
(κ) denote the families of the minimizers of p :2
C
→
Z and κ :2
V
+
∪V
−
→ Z, respectively. 2
Remark 4.2.21. By combining Theorem 4.2.18, the above relation (4.26),
and the general min-max theorem for the independent matching problem
(Theorem 2.3.27 or (2.72)), we obtain
rank A = max
M: indep.
matching
|M| = min
U
κ(U) = min
J
p(J)+|C|.

4.2 Rank of Mixed Matrices 145
This argument affords an alternative proof of the rank formula of Theorem
4.2.5, though the min-max theorem for the independent matching problem is
almost equivalent to the matroid union/partition theorem of Edmonds used
in deriving Theorem 4.2.5. Note that the relation (4.26) has been derived
independently of Theorem 4.2.5. 2
4.2.4 Algorithms for the Rank
Algorithm for LM-matrices. An efficient (polynomial time) algorithm
is described here which computes the rank of an LM-matrix A =
.
Q
T
/
∈
LM(K, F ; m
Q
,m
T
,n). On the basis of Theorem 4.2.18 the algorithm solves
the associated independent matching problem by specializing the general al-
gorithmic scheme described in §2.3.5.
Recall that the associated independent matching problem is defined on
the bipartite graph G =(V
+
,V
−
; E)=(R
T
∪C
Q
,C; E
T
∪E
Q
), where R
T
=
Row(T ), C = Col(A), C
Q
is a disjoint copy of C (with j
Q
∈ C
Q
denoting the
copy of j ∈ C), and
E
T
= {(i, j) | i ∈ R
T
,j ∈ C, T
ij
=0},E
Q
= {(j
Q
,j) | j ∈ C}.
The algorithm works with a directed graph
˜
G =
˜
G
M
=(
˜
V,
˜
E) with vertex
set
˜
V = R
T
∪C
Q
∪C and arc set
˜
E = E
T
∪E
Q
∪E
+
∪M
◦
, where E
+
and M
◦
are defined and updated in the algorithm; E
+
represents the structure of the
matroid M(Q)andM
◦
expresses an independent matching M ⊆ E
T
∪E
Q
as
M
◦
= {a | a ∈ M} (a: reorientation of a).
It is noted that the arcs in E
+
have both ends in C
Q
and the arcs in M
◦
are
directed from C to R
T
∪ C
Q
, i.e., ∂
+
M
◦
⊆ C and ∂
−
M
◦
⊆ R
T
∪ C
Q
.
Since M is an independent matching, I = {i ∈ C | i
Q
∈ ∂
−
M
◦
∩ C
Q
} is
an independent set of M(Q), whereas we denote by J the set of elements of
C \ I which are dependent on I in M(Q). Namely,
rank Q[R
Q
,I]=|I|,J= {j ∈ C \ I | rank Q[R
Q
,I ∪{j}]=|I|}.
Besides the graph
˜
G we use a matrix (or two-dimensional array) P and
a vector (or one-dimensional array) base to implement the structure of the
matroid M(Q). The array P represents a matrix over K,ofsizem
Q
× n,
which is obtained from Q by row-transformations; we have P = Q at the
beginning of the algorithm (Step 1 below). The variable base is a vector of
size m
Q
, which represents a mapping (correspondence): R
Q
→ C ∪{0}.The
sets I and J are represented as
I = {i ∈ C | i = base[h] =0,h ∈ R
Q
},
J = {j ∈ C \ I |∀h : base[h]=0⇒ P [h, j]=0}.
146 4. Theory and Application of Mixed Matrices
For i ∈ I and j ∈ J, I −i+j is independent in M(Q) if and only if P [h, j] =0
for the h ∈ R
Q
such that i = base[h]. Optionally, it computes an m
Q
× m
Q
matrix S over K such that SQ = P . If such information is not needed, the
matrix S may simply be eliminated from the computation without any side
effect.
The entrance S
+
⊆
˜
V and the exit S
−
⊆
˜
V are defined by
S
+
=(R
T
\ ∂
−
M
◦
) ∪{j
Q
∈ C
Q
| j ∈ C \ (I ∪ J)},S
−
= C \ ∂
+
M
◦
.
The algorithm looks for a shortest path from the entrance S
+
to the exit S
−
to augment the matching M.
Algorithm for computing the rank of an LM-matrix A
Step 1:
M
◦
:= ∅; base[i]:=0(i ∈ R
Q
); P[i, j]:=Q
ij
(i ∈ R
Q
,j ∈ C);
S := unit matrix of order m
Q
.
Step 2:
I := {i ∈ C | i
Q
∈ ∂
−
M
◦
∩ C
Q
};
J := {j ∈ C \ I |∀h : base[h]=0⇒ P [h, j]=0};
S
+
T
:= R
T
\ ∂
−
M
◦
; S
+
Q
:= {j
Q
∈ C
Q
| j ∈ C \ (I ∪ J)};
S
+
:= S
+
T
∪ S
+
Q
; S
−
:= C \ ∂
+
M
◦
;
E
+
:= {(i
Q
,j
Q
) | h ∈ R
Q
,j ∈ J, P [h, j] =0,i= base[h] =0};
[
˜
E is updated accordingly]
If there exists in
˜
G =(
˜
V,
˜
E) a directed path from S
+
to S
−
then go to
Step 3; otherwise (including the case where S
+
= ∅ or S
−
= ∅) stop with
the conclusion that rank A = |M
◦
|.
Step 3:
Let L (⊆
˜
E) be (the set of arcs on) a shortest path from S
+
to S
−
(“shortest” in the number of arcs);
M
◦
:= (M
◦
\L) ∪{(j, i) | (i, j) ∈ L ∩ E
T
}∪{(j, j
Q
) | (j
Q
,j) ∈ L ∩ E
Q
};
If the initial vertex (∈ S
+
) of the path L belongs to S
+
Q
, then do the
following:
{Let j
Q
(∈ S
+
Q
⊆ C
Q
) be the initial vertex;
Find h such that base[h]=0andP [h, j] =0;
[j ∈ C corresponds to j
Q
∈ C
Q
]
base[h]:=j; w := 1/P [h, j];
P [k, l]:=P [k, l] − w × P [k, j] × P [h, l](k ∈ R
Q
\{h},l ∈ C \{j});
S[k,l]:=S[k,l] − w × P [k, j] × S[h, l](k ∈ R
Q
\{h},l ∈ R
Q
);
P [k, j]:=0 (k ∈ R
Q
\{h}) };
For all (i
Q
,j
Q
) ∈ L ∩ E
+
(in the order from S
+
to S
−
along L)dothe
following:
{Find h such that i = base[h]; [j ∈ C corresponds to j
Q
∈ C
Q
]
base[h]:=j; w := 1/P [h, j];
P [k, l]:=P [k, l] − w × P [k, j] × P [h, l](k ∈ R
Q
\{h},l ∈ C \{j});
S[k,l]:=S[k,l] − w × P [k, j] × S[h, l](k ∈ R
Q
\{h},l ∈ R
Q
);

4.2 Rank of Mixed Matrices 147
P [k, j]:=0 (k ∈ R
Q
\{h}) };
Go to Step 2. 2
In the above algorithm, ∂
+
M
◦
∩C is an independent set in M(Q)∨M(T ),
since I is independent in M(Q) and (∂
+
M
◦
∩C) \I is independent in M(T).
Since M(Q) ∨M(T )=M(A) by Theorem 4.2.3, we have rank A[R, ∂
+
M
◦
∩
C]=|M
◦
|. At each execution of Step 3 the size of M
◦
increases by one, and
at the termination of the algorithm we have the relation: rank A = |M
◦
|.
The updates of P in Step 3 are the standard pivoting operations on
P , which is a matrix over the subfield K. The sparsity of P should be
taken into account in actual implementations of the algorithm. Computa-
tional techniques developed for solving sparse linear programs can be uti-
lized here. As indicated in Step 3, pivoting operations are required for each
arc (i
Q
,j
Q
) ∈ L ∩E
+
. It is important to traverse the path L from S
+
to S
−
,
not from S
−
to S
+
, to avoid unnecessary fill-ins. See Murota–Scharbrodt
[241] for other implementation issues.
The above algorithm uses arithmetic operations in the subfield K only,
and, according to the result of Cunningham [43], runs in O(n
3
log n), where
m = m
Q
+ m
T
=O(n) is assumed for simplicity in this complexity bound.
The algorithm will be efficient enough for practical applications (see §4.4.6).
Theoretically (but not practically) the rank of an LM-matrix can be com-
puted in (n
2.62
) time, according to Gabow and Xu [84].
Example 4.2.22. The algorithm above is illustrated here for the 4 ×5LM-
matrix used in Example 4.2.19:
A =
Q
T
=
x
1
x
2
x
3
x
4
x
5
11110
02110
f
1
t
1
000t
2
f
2
0 t
3
00t
4
where Col(A)=C = {x
1
,x
2
,x
3
,x
4
,x
5
} and Row(T )=R
T
= {f
1
,f
2
}.We
work with a 2 × 5 matrix P ,a2× 2 matrix S,andavectorbase of size 2.
The copy of C is denoted as C
Q
= {x
1Q
,x
2Q
,x
3Q
,x
4Q
,x
5Q
}.
The flow of computation is traced below.
Step 1: M
◦
:= ∅;
base :=
r
1
0
r
2
0
,
P :=
x
1
x
2
x
3
x
4
x
5
r
1
11110
r
2
02110
,
S :=
10
01
.
Step 2: I := ∅; J := {x
5
};
S
+
T
:= {f
1
,f
2
}; S
+
Q
:= {x
1Q
,x
2Q
,x
3Q
,x
4Q
};
S
+
:= {f
1
,f
2
,x
1Q
,x
2Q
,x
3Q
,x
4Q
}; S
−
:= {x
1
,x
2
,x
3
,x
4
,x
5
};
E
+
:= ∅;
There exists a path from S
+
to S
−
. [See
˜
G
(0)
in Fig .4.2]
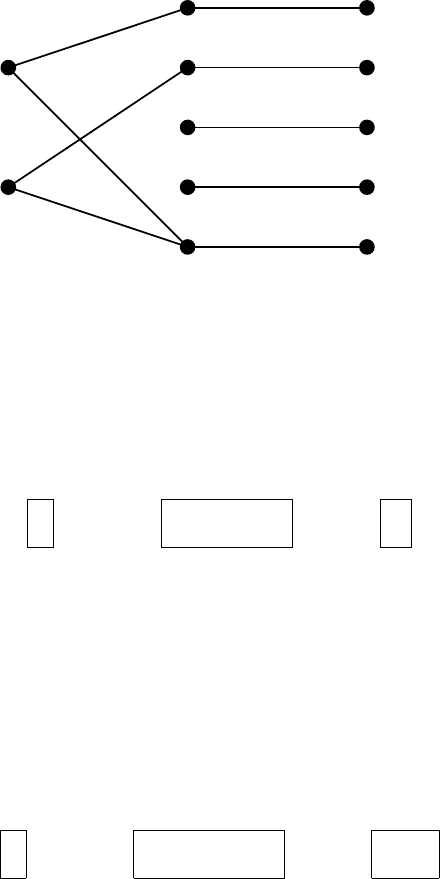
148 4. Theory and Application of Mixed Matrices
R
T
CC
Q
E
T
E
Q
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
+
+
−
−
−
−
−
+
+
+
+
1
R
3
q
Fig. 4.2. Graph
˜
G
(0)
(+: vertex in S
+
; −:vertexinS
−
)
Step 3: L := {(x
1Q
,x
1
)}; M
◦
:= {(x
1
,x
1Q
)};
The initial vertex x
1Q
of L is in S
+
Q
, and the matrices are updated (with
h = r
1
)to
base :=
r
1
x
1
r
2
0
,
P :=
x
1
x
2
x
3
x
4
x
5
r
1
11110
r
2
02110
,
S :=
10
01
.
Noting L ∩ E
+
= ∅ we return to Step 2.
Step 2: I := {x
1
}; J := {x
5
};
S
+
T
:= {f
1
,f
2
}; S
+
Q
:= {x
2Q
,x
3Q
,x
4Q
}; S
+
:= {f
1
,f
2
,x
2Q
,x
3Q
,x
4Q
};
S
−
:= {x
2
,x
3
,x
4
,x
5
};
E
+
:= ∅;
There exists a path from S
+
to S
−
. [See
˜
G
(1)
in Fig. 4.3]
Step 3: L := {(x
2Q
,x
2
)}; M
◦
:= {(x
1
,x
1Q
), (x
2
,x
2Q
)};
The initial vertex x
2Q
of L is in S
+
Q
, and the matrices are updated (with
h = r
2
)to
base :=
r
1
x
1
r
2
x
2
,
P :=
x
1
x
2
x
3
x
4
x
5
r
1
101/21/20
r
2
02 1 1 0
,
S :=
1 −1/2
01
.
Noting L ∩ E
+
= ∅ we return to Step 2.
Step 2: I := {x
1
,x
2
}; J := {x
3
,x
4
,x
5
};
S
+
T
:= {f
1
,f
2
}; S
+
Q
:= ∅; S
+
:= {f
1
,f
2
}; S
−
:= {x
3
,x
4
,x
5
};
E
+
:= {(x
1Q
,x
3Q
), (x
1Q
,x
4Q
), (x
2Q
,x
3Q
), (x
2Q
,x
4Q
)};
There exists a path from S
+
to S
−
. [See
˜
G
(2)
in Fig. 4.4]
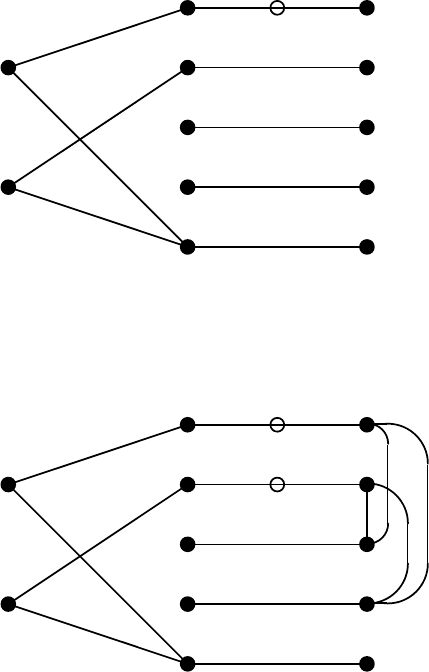
4.2 Rank of Mixed Matrices 149
R
T
CC
Q
E
T
E
Q
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
+
+
−
−
−
−
+
+
+
1
R
3
q
-
Fig. 4.3. Graph
˜
G
(1)
(:arcinM;+:vertexinS
+
; −:vertexinS
−
)
R
T
CC
Q
E
T
E
Q
E
+
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
+
+
−
−
−
1
R
3
q
-
-
?
?
?
?
Fig. 4.4. Graph
˜
G
(2)
(:arcinM;+:vertexinS
+
; −:vertexinS
−
)
Step 3: L := {(f
1
,x
5
)}; M
◦
:= {(x
1
,x
1Q
), (x
2
,x
2Q
), (x
5
,f
1
)};
The initial vertex f
1
∈ S
+
Q
and L ∩ E
+
= ∅, and therefore the matrices
remain unchanged and we return to Step 2.
Step 2: I := {x
1
,x
2
}; J := {x
3
,x
4
,x
5
};
S
+
T
:= {f
2
}; S
+
Q
:= ∅; S
+
:= {f
2
}; S
−
:= {x
3
,x
4
};
E
+
:= {(x
1Q
,x
3Q
), (x
1Q
,x
4Q
), (x
2Q
,x
3Q
), (x
2Q
,x
4Q
)};
There exists a path from S
+
to S
−
. [See
˜
G
(3)
in Fig. 4.5]
Step 3: L := {(f
2
,x
2
), (x
2
,x
2Q
), (x
2Q
,x
3Q
), (x
3Q
,x
3
)};
M
◦
:= {(x
1
,x
1Q
), (x
3
,x
3Q
), (x
5
,f
1
), (x
2
,f
2
)};
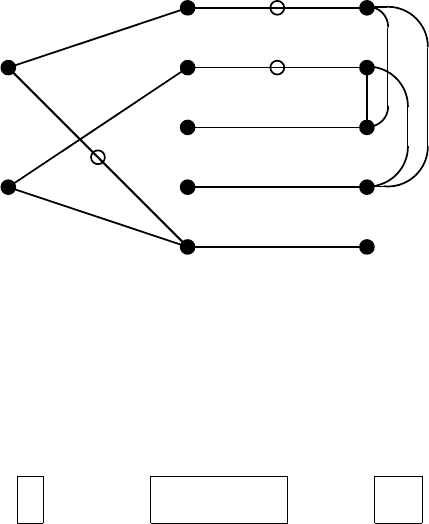
150 4. Theory and Application of Mixed Matrices
R
T
CC
Q
E
T
E
Q
E
+
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
+
−
−
1
R
3
q
-
-
I
?
?
?
?
Fig. 4.5. Graph
˜
G
(3)
(:arcinM;+:vertexinS
+
; −:vertexinS
−
)
The initial vertex f
2
∈ S
+
Q
and L ∩E
+
= {(x
2Q
,x
3Q
)}, and the matrices
are updated (with h = r
2
)to
base :=
r
1
x
1
r
2
x
3
,
P :=
x
1
x
2
x
3
x
4
x
5
r
1
1 −10 0 0
r
2
02110
,
S :=
1 −1
01
.
Step 2: I := {x
1
,x
3
}; J := {x
2
,x
4
,x
5
};
S
+
T
:= ∅; S
+
Q
:= ∅; S
+
:= ∅; S
−
:= {x
4
};
E
+
:= {(x
1Q
,x
2Q
), (x
3Q
,x
2Q
), (x
3Q
,x
4Q
)};
There exists no path from S
+
(= ∅)toS
−
;
We stop with the conclusion that rank A = |M
◦
| =4.
[See
˜
G
(4)
in Fig. 4.6]
2
Remark 4.2.23. It is easy to observe that the arcs in M, directed from
R
T
∪C
Q
to C, are never used in the shortest path from S
+
to S
−
, whereas the
reoriented arcs, implemented as M
◦
, are indispensable. This means that the
arcs of M could have been eliminated in the above algorithm for computing
the rank. They are included, however, for the consistency with the algorithm
for computing the CCF, to be presented in §4.4.4, in which the arcs of M are
necessary. 2
Algorithm for Mixed Matrices. The rank of a mixed matrix A = Q + T
can be computed by applying the above algorithm to the associated LM-
matrix
˜
A =
.
˜
Q
˜
T
/
of (4.4). Adaptation to the special form of
˜
A results in
some simplifications in the algorithm. Put R =Row(A)andC = Col(A).
