Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

3.1 Mixed Matrix for Modeling Two Kinds of Numbers 111

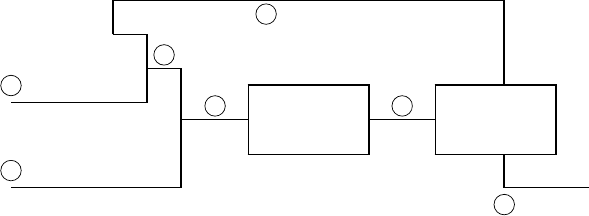
Example 3.1.3 (Ethylene dichloride production system). Consider

a hypothetical system (Fig. 3.3) for the production of ethylene dichloride

), which is slightly modiﬁed from an example used in “Users’ Man-

ual of Generalized Interrelated Flow Simulation” of “The Service Bureau

Co.”

reactor

+Cl

−→ C

90 % conv. of C

puriﬁcation

chlorine feed

100 mol Cl

ethylene feed

100 mol C

recycle

product

Fig. 3.3. Hypothetical ethylene dichloride production system of Example 3.1.3

Feeds to the system are 100 mol/h of pure chlorine (Cl

) (stream 1), and

100 mol/h of pure ethylene (C

) (stream 2). In the reactor, 90% of the

input ethylene is converted into ethylene dichloride according to the reaction

formula

+Cl

→ C

. (3.4)

At the puriﬁcation stage, the product ethylene dichloride is recovered and

the unreacted chlorine and ethylene are separated for recycle. The degree of

puriﬁcation is described in terms of component recovery ratios a

, a

and

of chlorine, ethylene and ethylene dichloride, respectively, which indicate

the ratios of the amounts recovered in stream 6 of the respective components

over those in stream 5.

We now consider the following problem.

[Problem] Given the component recovery ratios a

and a

of chlo-

rine and ethylene, determine the recovery ratio x = a

of ethylene

dichloride with which a speciﬁed production rate y mol/h of ethylene

dichloride is realized.

Let u

, u

and u

mol/h be the component ﬂow rates of chlorine, ethy-

lene and ethylene dichloride in stream i, respectively. The system of equations

to be solved may be put in the following form, where u is an auxiliary variable

in the reactor and r (= 0.90) is the conversion ratio of ethylene:

112 3. Physical Observations for Mixed Matrix Formulation

str3=str1+str6: u

= u

+ 100,

= u

(j =2, 3);

str4=str2+str3: u

= u

+ 100,

= u

(j =1, 3);

reactor: u = ru

= u

− u (j =1, 2),

= u

+ u,

puriﬁcation: u

= a

(j =1, 2),

= xu

= u

− u

(j =1, 2),

y = u

− u

(3.5)

This is a system of linear/nonlinear equations in unknown variables x, u

and u

, where the equation “u

= xu

” in the puriﬁcation is the only

nonlinear equation. We may regard a

(j =1, 2) and r (= 0.90) as inaccurate

and independent numbers. It should be noted in this example that, in the

chemical reaction formula of (3.4), we encounter accurate numbers, ±1, as

the integer coeﬃcients in the reaction formula, which are sometimes called

the “stoichiometric coeﬃcients.” The Jacobian matrix J of (3.5) is shown in

Fig. 3.4, and the solvability of (3.5) will be discussed in §4.3.3. 2

y 1 −1

−11

1 −1

1 −1 −1

1 −11

−1

x −1

1 −1 −1

u r −1

Fig. 3.4. Jacobian matrix of (3.5) (chemical process simulation in Example 3.1.3)

As illustrated by the examples above, the accurate numbers often ap-

pear in equations for conservation laws such as Kirchhoﬀ’s laws, the law of

conservation of mass, energy or momentum, and the principle of action and

reaction, where the nonvanishing coeﬃcients are either 1 or −1, representing

the underlying topological incidence relations. Another typical example is the

integer coeﬃcients, i.e., the stoichiometric coeﬃcients, in chemical reactions.

3.1 Mixed Matrix for Modeling Two Kinds of Numbers 113

If we consider a gyrator in electrical networks, which has the element

characteristic represented by







0 r





the ratio r

is exactly equal to −1. Thus, accurate numbers arise also

as ratios of inaccurate numbers, or in other words, as numbers representing

mutual dependence among quantities which may be inaccurate by themselves.

(Electrical networks containing gyrators are treated in §7.3.5.)

When we deal with dynamical systems, we encounter another example

of accurate numbers which represent the deﬁning relations such as those

between velocity v and position x and between current ξ and charge Q:

v =1·

,ξ=1·

Typical accurate numbers have been illustrated in Fig. 1.4.

To sum up, we can distinguish between accurate numbers and inaccurate

numbers. We may alternatively refer to the numbers of the ﬁrst kind as “ﬁxed

constants” and to those of the second kind as “system parameters.” For easy

reference we reiterate this distinction below:

Accurate numbers (ﬁxed constants): Numbers accounting for various sorts of

conservation laws such as Kirchhoﬀ’s laws which, stemming from topo-

logical incidence relations, are precise in value (often ±1).

Inaccurate numbers (system parameters): Numbers representing independent

physical parameters such as resistances in electrical networks and masses

in mechanical systems which, being contaminated with noise and other

errors, take values independent of one another.

In the above, we have explained informally what we mean by “two kinds

of numbers.” We now formulate this intuitive concept in more mathematical

terms referring to a pair of nested ﬁelds.

Let us denote by D the (multi)set of ﬁnitely many numbers characterizing

a system in question. Typically, for a linear system, the set of entries of the

coeﬃcient matrix may be taken for D. As the basic assumption we postulate

that the numbers in D are contained in a ﬁeld F , i.e.,

Basic Assumption: D⊆F , (3.6)

where it is assumed that F contains Q (the ﬁeld of rational numbers).

In addition to the ﬁeld F we consider a subﬁeld K of F :

Q ⊆ K ⊆ F (3.7)

with the intention that accurate numbers should belong to K and inaccurate

ones to F \ K. Accordingly, the set D is divided into two disjoint subsets

(multisets) as

114 3. Physical Observations for Mixed Matrix Formulation

D = Q∪T (3.8)

with

Q = D∩K, T = D\K. (3.9)

Our physical intuition that inaccurate numbers are independent of one an-

other can be translated into a mathematical statement:

Generality Assumption: T is algebraically independent over K. (3.10)

Assuming the algebraic independence of T is equivalent to regarding the

members of T as independent parameters, and therefore to considering the

family of systems parametrized by those parameters in T .

We have so far assumed that the subﬁeld K was given a priori. In practical

situations, however, the choice of K is in some sense at our disposal and

the statement (3.10) is adopted as a mathematical assumption in system

modeling. That is, how to choose the subﬁeld K in a real problem is not a

matter of mathematics but is determined by how we model that problem. In

contrast, the underlying ﬁeld F is just a mathematical formality and it may

be chosen to be suﬃciently large.

For instance, in Example 3.1.1 above we may choose K = Q, F =

Q(r

) and assume that T = {r

} satisﬁes (3.10).

In Example 3.1.2, we may take K = Q, F = Q(g

,α,β)andT =

,α,β}. A reasonable choice in Example 3.1.3 would be K = Q,

F = Q(a

,r,x,u

)andT = {a

,r,x,u

Here are three generality assumptions that may possibly be adopted in

system modeling. The ﬁrst is

GA1: The nonvanishing elements of D are algebraically independent

over Q.

This requires that (3.10) should hold for K = Q and T = D\{0}.The

generality assumption GA1 seems to be too stringent to be literally satis-

ﬁed in practical situations, but is convenient for graph-theoretic methods for

structural analysis such as those described in §1.1.2 and §4.3.2. The second

GA2: Those elements of D which do not belong to the rational num-

ber ﬁeld Q are algebraically independent over Q.

This requires that (3.10) should hold for K = Q and T = D\Q. The gener-

ality assumption GA2 is appropriate in many cases, including Examples 3.1.1

to 3.1.3 above, and will be adopted mostly in this book. The third is

GA3: Those elements of D which do not belong to the real number

ﬁeld R are algebraically independent over R.

This requires that (3.10) should hold for K = R and T = D\R.The

generality assumption GA3 will be useful in dealing with a system of lin-

ear/nonlinear equations, where D denotes the set of partial derivatives (en-

tries of the Jacobian matrix). Taking notice of the fact that the derivatives

3.1 Mixed Matrix for Modeling Two Kinds of Numbers 115

of linear functions are (real) constants, we classify the partial derivatives D

into constants and nonconstants; the latter standing for nonlinearity. This

classiﬁcation conforms to the above choice of K = R. See also Remark 1.3.1.

It is important to recognize here that a generality assumption is con-

cerned with the property of a mathematical description of a real system, and

not of the system itself. The assumption GA2, for example, is often justiﬁed

when the system in question is described by a collection of elementary re-

lations among elementary variables rather than by a compact sophisticated

representation. In Example 3.1.3, for instance, the auxiliary variable u in the

reactor of (3.5) could have been eliminated, the reactor being then described

more compactly by

= u

− ru

(j =1, 2),u

= u

+ ru

If the system were so described, the assumption GA2 is no longer valid even

if we may assume that r is independent of other quantities. In fact, the three

occurrences of one and the same r themselves could never be independent of

each other. The issue of mathematical description against generality assump-

tion will be considered again for dynamical systems in §3.1.2.

Remark 3.1.4. In the above argument we have assumed that the subﬁeld

K is chosen from physical considerations in mathematical modeling. From

the mathematical point of view, however, we may think of the following

problem: Given D⊆F , ﬁnd a subﬁeld K and a bipartition D = Q∪T such

that Q⊆K and T is algebraically independent over K. It is not diﬃcult to

see that there exist a largest subset T and a smallest subﬁeld K that satisfy

these conditions, and they are given by

T = {t ∈D|t is transcendental over Q(D\{t})}, (3.11)

K = Q(D\T). (3.12)

The expressions (3.11) and (3.12) can be derived from a matroid-theoretic

consideration as follows (see §2.3.2 for matroid-theoretic terms). Let M be the

algebraic matroid (see Example 2.3.10) deﬁned on D with respect to algebraic

independence over Q. For a given T , (3.12) is an obvious choice of the smallest

K to meet the condition that Q = D\T ⊆K. Then the condition (3.10) is

equivalent to the statement that T is independent in the contraction of M

to T . This statement is tantamount to saying that T consists of coloops of

M. It follows, therefore, that the largest T is given by (3.11). 2

Remark 3.1.5. Some comments would be in order here on the mutual re-

lations among the generality assumptions GA1, GA2 and GA3 above. First

of all, GA2 is weaker than GA1; that is, if D satisﬁes GA1, it satisﬁes GA2,

too. No other implications exist, as exempliﬁed below, where F = R(x, e

)

and T of (3.11) is also given. Note that the algebraic independence of

,x,e

√

, e

√

} over Q follows from Theorem 3.1.6 below.

116 3. Physical Observations for Mixed Matrix Formulation

D GA1 GA2 GA3 T

,x,e

√

, e

√

} yes yes yes {e

,x,e

√

, e

√

}

,x,e

√

x, e

√

} yes yes no {e

,x,e

√

x, e

√

}

,x,π,1} no yes yes {e

,x,π}

{x, π, π

√

2} no no yes {x}

,x,πx,1} no yes no {e

,x,πx}

,x,πx,π} no no no {e

}

This example is given for mathematical completeness, and not for physical

signiﬁcance. 2

Theorem 3.1.6 (Lindemann–Weierstrass theorem). Let y

, ···,y

algebraic numbers over Q that are linearly independent over Q. Then the set

{exp y

, ···, exp y

} is algebraically independent over Q.

Proof. See, e.g., Jacobson [148, 149].

3.1.2 Mixed Matrix and Mixed Polynomial Matrix

The distinction of two kinds of numbers can be embodied in the concept

of mixed matrices. It is generalized to another concept of mixed polynomial

matrices to deal with dynamical systems.

Consider a matrix A over a ﬁeld F and denote by D the set of its entries.

With reference to a subﬁeld K of F , the set D is divided into two parts,

D = Q∪T by (3.9), and accordingly, the matrix A is expressed as A = Q+T ,

where T is the set of the nonzero entries of T . The generality assumption

(3.10) then amounts to an assumption of the algebraic independence over K

of the nonzero entries of T . This leads to the following formal deﬁnition.

Let K be a subﬁeld of a ﬁeld F .Anm×n matrix A over F (i.e., A

∈ F )

is called a mixed matrix with respect to (K, F )if

A = Q + T, (3.13)

where

(M-Q) Q is an m × n matrix over K (i.e., Q

∈ K), and

(M-T) T is an m ×n matrix over F (i.e., T

∈ F ) such that the set

T of its nonzero entries is algebraically independent over K.

We usually assume

=0 ⇒ Q

to make the decomposition (3.13) unique. The class of m × n mixed ma-

trices with respect to (K, F ) is denoted as MM(K, F ; m, n) (or simply as

MM(K, F )) and the subﬁeld K will be called the ground ﬁeld.

Mixed matrices are useful also in dealing with linear time-invariant dy-

namical systems. In this case, we encounter a ﬁeld composed of, say, the

3.1 Mixed Matrix for Modeling Two Kinds of Numbers 117

Laplace transforms, or a ﬁeld consisting of operators such as Heaviside’s and

Mikusi´nski’s.

Speciﬁcally, suppose that a dynamical system is written in the descriptor

form (Katayama [155], Luenberger [182, 183]):

= A x + B u, (3.14)

where x is an n-dimensional vector called the descriptor-vector, u is an m-

dimensional input-vector, and F , A and B are n × n, n × n,andn × m

matrices, respectively. The Laplace transform of the equation (3.14) gives a

frequency domain description:

sF x = A x + B u, or



A − sF B







= 0, (3.15)

where x(0) = 0, u(0) = 0 is assumed (see Remark 1.1.1 for the Laplace

transform).

Suppose further that the generality assumption GA2 is acceptable. Then

the matrices F , A and B are mixed matrices with ground ﬁeld Q:

F = Q

+ T

,A= Q

+ T

,B= Q

+ T

such that the set of the nonvanishing entries of [T

| T

] is algebraically

independent over Q.

The coeﬃcient matrix D(s)=[A − sF | B] in the frequency domain

description is a polynomial matrix (a matrix pencil) with the expression

D(s)=D

+ sD

where the coeﬃcient matrices, D

and D

, are mixed matrices expressed as

=[A | B]=[Q

| Q

]+[T

| T

=[−F | O]=[−Q

| O]+[−T

| O].

Such matrix as D(s) is called a mixed polynomial matrix (a formal deﬁnition

is given later).

The matrix D(s)=[A −sF | B] is also a mixed matrix with ground ﬁeld

K = Q(s), since the expression

D(s)=Q(s)+T (s) (3.16)

with

Q(s)=[Q

− sQ

| Q

],T(s)=[T

− sT

| T

]

satisﬁes the conditions (M-Q) and (M-T), in spite of the occurrences of the

symbol s in both of the matrices Q(s)andT (s).

118 3. Physical Observations for Mixed Matrix Formulation

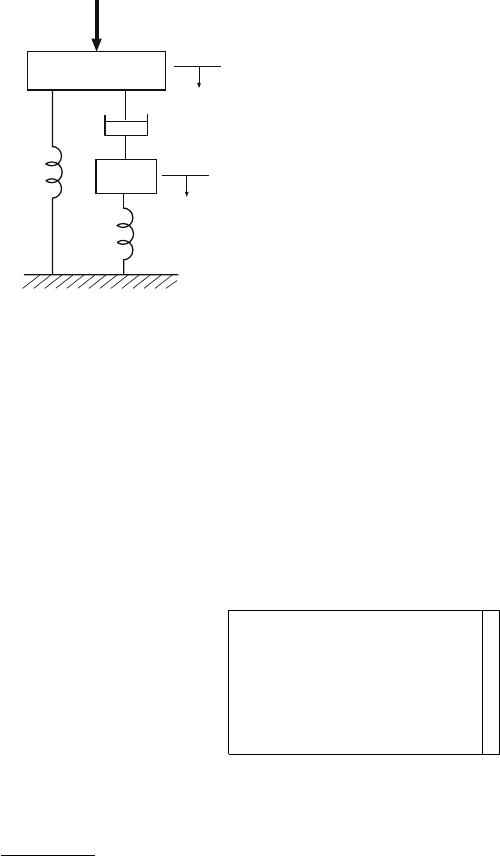
Example 3.1.7. Consider the mechanical system

in Fig. 3.5 consisting of

two masses m

and m

, two springs k

and k

, and a damper f ; u is the

force exerted from outside. We may choose x =(x

)asthe

descriptor-vector, where x

(resp. x

) is the vertical displacement (down-

wards) of mass m

(resp. m

), x

(resp. x

) is its velocity, x

is the force by

the damper f,andx

is the relative velocity of the two masses.

Fig. 3.5. A mechanical system of Exam-

ple 3.1.7

Then the system can be expressed in the descriptor form (3.14) with

F =

⎡

⎢

⎣

10 0 000

01 0 000

00m

000

00 0m

00 0 000

1 −10 000

⎤

⎥

⎦

,A=

⎡

⎢

⎣

001000

000100

−k

000−10

0 −k

00 1 0

0000−1 f

000001

⎤

⎥

⎦

,B=

⎡

⎢

⎣

⎤

⎥

⎦

. (3.17)

The matrix D(s)=[A − sF | B] is given as

D(s)=

−s 01 0000

0 −s 01000

−k

0 −sm

0 −101

0 −k

0 −sm

100

00 0 0−1 f 0

−ss 00010

If we regard {m

,f} as independent free parameters, i.e., as being

algebraically independent, the additive decomposition D(s)=Q(s)+T (s)in

(3.16) is given by

This mechanical system has been considered in §1.2.2.

3.1 Mixed Matrix for Modeling Two Kinds of Numbers 119

Q(s)=

−s 010000

0 −s 01 0 00

0000−101

0000100

0000−100

−ss 00 0 10

, (3.18)

T (s)=

00 0 0000

−k

0 −sm

0000

0 −k

0 −sm

000

00 0 00f 0

00 0 0000

. (3.19)

In this way the mechanical system can be described by means of a mixed

polynomial matrix with an appropriate choice of variables and equations.

The mechanical system could be described more compactly in the stan-

dard form (

A − sI

)

x +

Bu = 0 in terms of a four-dimensional state-vector

x =(x

) and the input-vector u =(u). In such a compact rep-

resentation, however, the generality assumptions will not be acceptable. In

fact, the coeﬃcient matrix

[

A − sI

B]=

−s 01 00

0 −s 010

−k

0 −f/m

− sf/m

1/m

0 −k

f/m

−f/m

− s 0

may not be regarded as a mixed matrix.

This mechanical system will be considered again in Example 3.2.2. 2

The above argument can be extended to a linear time-invariant dynamical

system described by a polynomial matrix

A(s)=



k=0

The variable s here is primarily intended to mean the variable for the Laplace

transform for continuous-time systems, though it could be interpreted as

the variable for the z-transform for discrete-time systems (see Chen [33],

Zadeh–Desoer [350] for the z-transform). In such reprepresentation, it is often

justiﬁed to assume that the coeﬃcient matrices A

(k =0, 1, ···,N)are

expressed in the form

= Q

+ T

(k =0, 1, ···,N)

such that

120 3. Physical Observations for Mixed Matrix Formulation

(MP-Q1) Q

(k =0, 1, ···,N) are matrices over K,and

(MP-T) T

(k =0, 1, ···,N) are matrices over F such that the set

T of their nonzero entries is algebraically independent over K.

Then A(s) is split accordingly into two parts:

A(s)=Q(s)+T (s) (3.20)

with

Q(s)=



k=0

,T(s)=



k=0

Such a matrix A(s) will be called a mixed polynomial matrix with respect to

(K, F ). Obviously, each A

is a mixed matrix with respect to (K, F ). Also

note that A(s) is a mixed matrix with respect to (K(s), F (s)) in spite of the

occurrences of the symbol s in both of the matrices Q(s)andT (s).

In §3.2 we will discuss more on the mixed polynomial matrices from the

viewpoint of the dimensional analysis to arrive at the concept of physical

matrices.

Notes. This section is based on Murota–Iri [237, 238] as well as Murota

[204].

3.2 Algebraic Implication of Dimensional Consistency

3.2.1 Introductory Comments

The concept of physical dimensions would be counted among the most fun-

damental in recognizing the nature of physical quantities. The principle of

dimensional homogeneity claims that any equation describing a physical phe-

nomenon must be consistent with respect to physical dimensions. This princi-

ple constitutes the basis of dimensional analysis, which has long been known

to scientists and engineers, and has proved to be fruitful in various ﬁelds (de

Jong [46], Huntley [116], Langhaar [169], Schouten [289, Chap. VI]). It is

important to notice that we cannot talk of dimensional homogeneity before

we recognize the diﬀerence in the nature of quantities from the viewpoint of

physical dimensions.

Suppose a physical system is described by a system of equations, which

may in turn be expressed by a matrix when linearized if necessary. With

each entry of the matrix is associated a physical dimension in a physically

consistent manner.

It is pointed out in the present section that, by virtue of the principle of

dimensional homogeneity, the physically-dimensioned coeﬃcient matrix de-

scribing a physical system enjoys a kind of total unimodularity in a certain