Murota K. Matrices and Matroids for Systems Analysis
Подождите немного. Документ загружается.

80 2. Matrix, Graph, and Matroid
Since |B
1
\ B
| = |B \ B
|−1, the above claim contradicts our choice of
(B,B
) ∈D. Therefore we conclude D = ∅, completing the proof of the the-
orem. (See also Brualdi [23], Kung [167], Welsh [333] for alternative proofs.)
In connection to dual matroids we have seen in §2.3.2 another exchange
property
8
(BM
+
)ForB,B
∈Band for u ∈ B \ B
, there exists v ∈ B
\ B
such that B
+ u − v ∈B.
The next lemma shows that (BM
+
) also implies the simultaneous exchange
property (BM
±
).
Lemma 2.3.12. For B⊆2
V
, (BM
+
)=⇒ (BM
±
).
Proof. This is an immediate corollary to Lemma 2.3.11, since (BM
+
)forB
is equivalent to (BM
−
)forB
∗
= {V \ B | B ∈B}, and (BM
±
)forB is
equivalent to (BM
±
)forB
∗
.
We mention a weaker statement on simultaneous exchange:
(BM
±w
) For distinct B, B
∈B, there exist u ∈ B \B
and v ∈ B
\B
such that B −u + v ∈Band B
+ u − v ∈B.
The following fact was observed by Kelmans [156] (according to White [339])
and independently by Tomizawa [314].
Lemma 2.3.13. For B⊆2
V
, (BM
±w
)=⇒ (BM
−
).
Proof.TakeB, B
∈Band u ∈ B \ B
.By(BM
±w
) there exist u
1
∈ B \ B
and v
1
∈ B
\ B such that B − u
1
+ v
1
∈Band B
+ u
1
− v
1
∈B.Ifu
1
= u,
(BM
−
) is satisfied with v = v
1
. Otherwise, put B
= B
+ u
1
− v
1
∈B,for
which u ∈ B \ B
and |B
\B| = |B
\B|−1. Again by (BM
±w
) there exist
u
2
∈ B \B
and v
2
∈ B
\B such that B −u
2
+v
2
∈Band B
+u
2
−v
2
∈B.
If u
2
= u,(BM
−
) is satisfied with v = v
2
. Otherwise, continue the above
argument to eventually obtain a valid v ∈ B \B
.
The above lemmas imply the following theorem, stating the equivalence
among exchange properties. This means that any one of (BM
+
), (BM
−
),
(BM
±
), (BM
±w
) serves as an axiom of the basis family of a matroid.
Theorem 2.3.14. For B⊆2
V
, the exchange properties (BM
+
), (BM
−
),
(BM
±
), (BM
±w
) are equivalent.
Proof. Obviously, (BM
±
) ⇒ (BM
−
), (BM
±
) ⇒ (BM
+
) and (BM
±
) ⇒
(BM
±w
). We have (BM
−
) ⇒ (BM
±
) by Lemma 2.3.11, and (BM
+
) ⇒ (BM
±
)
by Lemma 2.3.12. Finally, (BM
±w
) ⇒ (BM
−
) by Lemma 2.3.13.
8
At first sight (BM
+
) here may appear different from the one in §2.3.2, but they
are identical through a change of notation B ↔ B
and u ↔ v.
2.3 Matroid 81
Remark 2.3.15. In the proof of Lemmas 2.3.11 and 2.3.12, we intentionally
avoided referring to rank functions. This is because the exchange proper-
ties play the major role in the argument of valuated matroids in §5.2. The
equivalence of (BM
±
) and (BM
±w
) remains valid for their generalizations in
valuated matroids (see Theorem 5.2.25) and the present proof technique is
generalized to prove it. 2
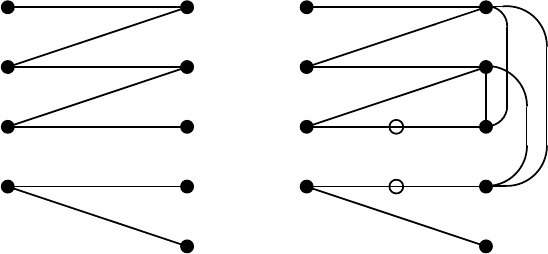
The simultaneous exchange property has an important consequence, as
observed by Brualdi [23]. For B ∈Band B
⊆ V we define the exchangeability
graph, denoted G(B, B
), as a bipartite graph (B \ B
,B
\ B; A)havingthe
vertex bipartition (B \B
,B
\ B) and the arc set
A = {(u, v) | u ∈ B \ B
,v ∈ B
\ B, B − u + v ∈B}. (2.66)
Lemma 2.3.16 (Perfect-matching lemma). Let B ∈B.IfB
is also a
base, then G(B, B
) has a perfect matching.
Proof. For any u
1
∈ B \B
there exists v
1
∈ B
\B such that B −u
1
+ v
1
∈B
and B
2
:= B
+ u
1
−v
1
∈B. By the same argument applied to (B,B
2
), there
exist u
2
∈ (B \B
) \{u
1
} and v
2
∈ (B
\B) \{v
1
} such that B −u
2
+ v
2
∈B
and B
3
:= B
2
+u
2
−v
2
= B
+{u
1
,u
2
}−{v
1
,v
2
}∈B. Repeating this process
we obtain B − u
i
+ v
i
∈B(i =1, ···,m), where m = |B \ B
| = |B
\ B|,
B \ B
= {u
1
, ···,u
m
} and B
\ B = {v
1
, ···,v
m
}.
The converse of the above statement is not always true, as follows.
Example 2.3.17. Consider the matroid M =(V,B) defined by a matrix
u
1
u
2
v
1
v
2
1011
0111
on the column set V = {u
1
,u
2
,v
1
,v
2
}.TakeB = {u
1
,u
2
} and B
=
{v
1
,v
2
}. Then B ∈Band B
∈B, whereas G(B,B
) is a complete bipar-
tite graph, admitting two perfect matchings, M
1
= {(u
1
,v
1
), (u
2
,v
2
)} and
M
2
= {(u
1
,v
2
), (u
2
,v
1
)}. 2
A partial converse of Lemma 2.3.16 holds in the following form.
Lemma 2.3.18 (Unique-matching lemma). Let B ∈Band B
⊆ V
with |B
| = |B|. If there exists exactly one perfect matching in G(B,B
),
then B
∈B.
Proof. The proof is given later based on a series of lemmas below.
First we note the following fact, rephrasing the existence of a unique
perfect matching with reference to suitable orderings of the elements of B \B
and B
\ B.

82 2. Matrix, Graph, and Matroid
Lemma 2.3.19. For B ∈Band B
⊆ V with |B
\ B| = |B \ B
| = m, the
graph G(B,B
) has a unique perfect matching if and only if there exist some
indexings of the elements of B \ B
and B
\ B,sayB \ B
= {u
1
, ···,u
m
}
and B
\ B = {v
1
, ···,v
m
}, such that B − u
i
+ v
i
∈B(1 ≤ i ≤ m) and
B − u
i
+ v
j
∈B(1 ≤ i<j≤ m).
Proof. This is immediate from the properties of the DM-decomposition de-
scribed in Theorem 2.2.22. Note that there exists a unique perfect matching
if and only if the tails are empty and each consistent DM-component is com-
posed of a single arc.
Lemma 2.3.20. Let B ∈Band u, u
◦
,v,v
◦
be four distinct elements with
{u, u
◦
}⊆B, {v, v
◦
}⊆V \ B,andputB
= B −{u, u
◦
} + {v, v
◦
}.IfM =
{(u, v), (u
◦
,v
◦
)} is the unique perfect matching in G(B,B
), then B
∈B.
Proof.PutB
◦
= B−u
◦
+v
◦
and B
∗
= B−u+v. By applying the simultaneous
exchange axiom to (B
◦
,B
∗
) with u ∈ B
◦
\ B
∗
we obtain B
∗
− v
+ u ∈B
and B
◦
+ v
− u ∈Bfor some v
∈ B
∗
\ B
◦
= {u
◦
,v}.Ifv
= u
◦
,wehave
B
∗
− u
◦
+ u = B − u
◦
+ v ∈Band B
◦
+ u
◦
− u = B − u + v
◦
∈B,which
means that M
= {(u
◦
,v), (u, v
◦
)} is another perfect matching in G(B, B
),
a contradiction to the uniqueness of M. Therefore we must have v
= v,and
then B
= B
◦
+ v − u ∈B.
Lemma 2.3.21. Let B ∈Band B
⊆ V with |B
| = |B|. If there exists
exactly one perfect matching M in G(B, B
), then for any (u
◦
,v
◦
) ∈ M it
holds that B
◦
≡ B −u
◦
+v
◦
∈Band there exists exactly one perfect matching
in G(B
◦
,B
).
Proof. The first assertion, B
◦
∈B, is obvious. Using the notation in Lemma
2.3.19 we have M = {(u
i
,v
i
) | i =1, ···,m} and (u
◦
,v
◦
)=(u
k
,v
k
) for some
k.Fori = k, j = k, put
B
ij
= B
◦
− u
i
+ v
j
= B −{u
i
,u
◦
} + {v
j
,v
◦
}.
Since G(B,B
ii
) has a unique perfect matching {(u
i
,v
i
), (u
◦
,v
◦
)},wehave
B
ii
∈Bby Lemma 2.3.20. We also claim that B
ij
∈Bif i<j.Tosee
this, suppose B
ij
∈B. Then Lemma 2.3.16 implies the existence of a perfect
matching in G(B,B
ij
), which is either M
1
= {(u
i
,v
j
), (u
◦
,v
◦
)} or M
2
=
{(u
i
,v
◦
), (u
◦
,v
j
)}.ButM
1
is possible only if i ≥ j and M
2
is possible only
if i ≥ k ≥ j. Hence G(B
◦
,B
) meets the condition in Lemma 2.3.19.
We are now in the position to prove the unique-matching lemma.
(Proof of Lemma 2.3.18) The proof is by induction on m = |B \B
|.The
case of m = 1 is obvious. So assume m ≥ 2. Take any (u
◦
,v
◦
) contained
in the unique perfect matching, and put B
◦
= B − u
◦
+ v
◦
. Lemma 2.3.21

2.3 Matroid 83
shows that B
◦
∈Band G(B
◦
,B
) has a unique perfect matching. Then the
induction hypothesis yields B
∈B. 2
As a corollary to the unique-matching lemma we obtain an exchange-
augmentation property for independent sets. Recall that I denotes the family
of independent sets of the matroid M =(V,B, I,ρ).
Lemma 2.3.22. Suppose that {u
1
, ···,u
m
}⊆I ∈Iand {v
0
,v
1
, ···,v
m
}⊆
V \ I,whereu
i
(1 ≤ i ≤ m) and v
j
(0 ≤ j ≤ m) are distinct. If I + v
0
∈I,
I + v
i
∈I(1 ≤ i ≤ m), I − u
i
+ v
i
∈I(1 ≤ i ≤ m) and I − u
i
+ v
j
∈I
(1 ≤ i<j≤ m), then I −{u
1
, ···,u
m
} + {v
0
,v
1
, ···,v
m
}∈I.
Proof.PutB = I + v
0
and B
= I −{u
1
, ···,u
m
}+ {v
0
,v
1
, ···,v
m
}. Then B
is a base of the truncation of M,sayM
=(V,B
), with rank M
= |I|+1. We
claim that B −u
i
+v
i
∈B
(1 ≤ i ≤ m)andB −u
i
+v
j
∈B
(1 ≤ i<j≤ m).
The former follows from
ρ(B − u
i
+ v
i
) ≥ ρ(I + v
0
+ v
i
)+ρ(I − u
i
+ v
i
) − ρ(I + v
i
)
=(|I| +1)+|I|−|I| = |I| +1,
whereas the latter is obvious from I − u
i
+ v
j
∈I(1 ≤ i<j≤ m).
Then Lemma 2.3.18 together with Lemma 2.3.19 implies that B
= B −
{u
1
, ···,u
m
} + {v
1
, ···,v
m
} belongs to B
, and hence to I.
Remark 2.3.23. In the case where the matroid is defined by a matrix, the
unique-matching lemma is a restatement of an obvious fact that a triangular
matrix having nonzero diagonal elements is nonsingular. Let M =(V,B)be
a matroid defined by a matrix A with V = Col(A) and rank A = |R|, where
R =Row(A). For B ∈Bdefine
˜
A = A[R, B]
−1
A, where it is noted that
Row(
˜
A) can be identified with B while Col(
˜
A)=V . Then B − u + v ∈Bif
and only if (u, v)entryof
˜
A is distinct from zero. For B
⊆ V with |B
| =
|B| = |R|, the graph G(B, B
) has a unique perfect matching if and only if the
rows (B \B
) and the columns (B
\B) of the submatrix
˜
A[B \B
,B
\B]can
be rearranged so that the resulting matrix may be a triangular matrix with
nonzero diagonal entries. If this is the case, the submatrix
˜
A[B \ B
,B
\ B]
is nonsingular, which corresponds to the nonsingularity of A[R, B
], i.e., the
condition B
∈B. 2
Remark 2.3.24. The unique-matching lemma reveals a key property un-
derlying the (unweighted or linear-weighted) matroid intersection algorithm,
to be explained later. In the literature (e.g., Iri–Tomizawa [133, Lemma 2],
Krogdahl [164], Lawler [171, Lemma 3.1 of Chap. 8], and Schrijver [291, The-
orem 4.3]) this fact is stated often with an explicit reference to the orderings
of the elements just as in Lemma 2.3.19 and Lemma 2.3.22, and is accordingly
referred to as “no-shortcut lemma” (cf. Kung [167] for this name). We have
adopted the present form, referring to the uniqueness of a perfect matching,
because this is suitable for its extension to valuated matroids in §5.2. 2

84 2. Matrix, Graph, and Matroid
2.3.5 Independent Matching Problem
The matroid intersection problem and its extensions will play a major role
in this book. The problem may be described as follows:
[Matroid intersection problem]
Given a pair of matroids M
1
and M
2
defined on a common ground
set V , find a common independent set of maximum size.
In this section we feature an equivalent variant of the matroid intersec-
tion problem called the independent matching problem, which is defined as
follows. Suppose we are given a bipartite graph G =(V
+
,V
−
; A) and two ma-
troids M
+
=(V
+
, B
+
, I
+
,ρ
+
)andM
−
=(V
−
, B
−
, I
−
,ρ
−
). Here, (V
+
,V
−
)
is the bipartition of the vertex set of G, A is the arc set of G; M
+
is a ma-
troid on V
+
with the family of bases B
+
, the family of independent sets I
+
,
and the rank function ρ
+
; and similarly for M
−
. Arcs are directed from V
+
to V
−
and therefore the initial vertex ∂
+
a ∈ V
+
and the terminal vertex
∂
−
a ∈ V
−
for each a ∈ A.
A matching M(⊆ A) is called an independent matching if
∂
+
M ∈I
+
,∂
−
M ∈I
−
, (2.67)
where ∂
+
M (resp., ∂
−
M) denotes the set of vertices in V
+
(resp., V
−
)in-
cident to M.Thatis,M(⊆ A) is an independent matching if and only if
|M| = |∂
+
M| = |∂
−
M| and the sets of end-vertices of M, i.e., ∂
+
M and
∂
−
M, are independent in M
+
and M
−
, respectively. The independent match-
ing problem is to find an independent matching M of maximum cardinality:
[Independent matching problem]
Find a matching M(⊆ A) that maximizes |M| subject to the con-
straint that ∂
+
M ∈I
+
and ∂
−
M ∈I
−
.
The matroid intersection problem above is a special case of the inde-
pendent matching problem, in which V
+
and V
−
are disjoint copies of V ,
M
+
M
1
, M
−
M
2
,andA = {(v
+
,v
−
) | v ∈ V }, where v
+
∈ V
+
and
v
−
∈ V
−
denote the copies of v ∈ V .
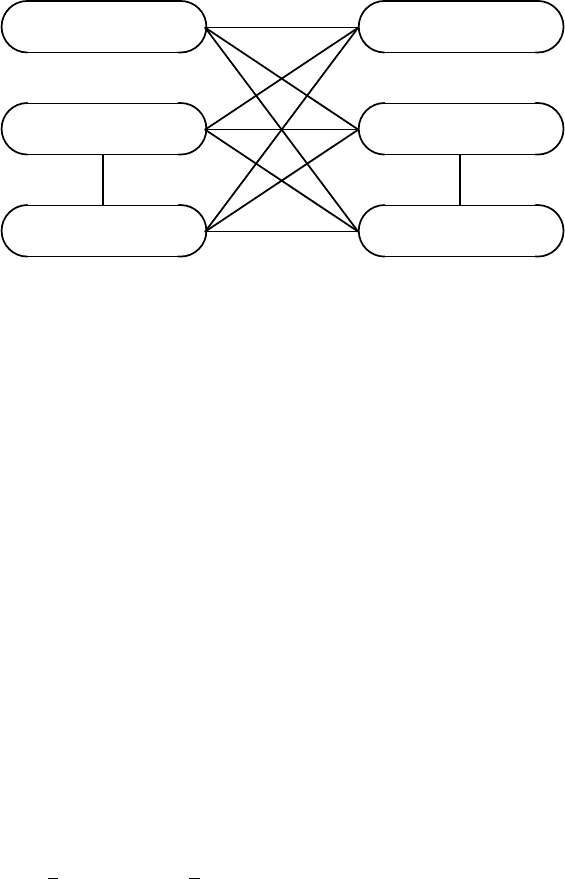
Example 2.3.25. Here is an example of the independent matching problem.
Consider a bipartite graph G =(V
+
,V
−
; A), shown in Fig. 2.8(a), with V
+
=
{x
1
,x
2
,x
3
,x
4
}, V
−
= {y
1
,y
2
,y
3
,y
4
,y
5
},andA = {(x
1
,y
1
), (x
2
,y
1
), (x
2
,y
2
),
(x
3
,y
2
), (x
3
,y
3
), (x
4
,y
4
), (x
4
,y
5
)}. The matroid M
+
is assumed to be a free
matroid on V
+
, whereas M
−
is a linear matroid defined by the matrix
y
1
y
2
y
3
y
4
y
5
11100
12010
00001
.
2.3 Matroid 85
Then M = {(x
3
,y
3
), (x
4
,y
4
)} is an independent matching with ∂
+
M =
{x
3
,x
4
} and ∂
−
M = {y
3
,y
4
} being independent in M
+
and M
−
, respec-
tively. Another matching M
= {(x
2
,y
2
), (x
3
,y
3
), (x
4
,y
4
)} is not an indepen-
dent matching, since ∂
−
M = {y
2
,y
3
,y
4
} is not independent in M
−
. 2
V
+
V
−
(a) Graph G
x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4
y
5
-
1
-
1
-
-
q
V
+
V
−
A
−
(b) Auxiliary graph
˜
G
M
x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4
y
5
+
+
−
-
1
-
1
-
-
q
?
?
?
?
Fig. 2.8. Graph G and auxiliary graph
˜
G
M
(:arcinM;+:vertexinS
+
; −:
vertex in S
−
)
The objective of this section is twofold:
1. To establish an extension of the min-max duality for bipartite matchings,
which has been formulated as the K¨onig–Egerv´ary theorem and the Hall–
Ore theorem, to that for independent matchings.
2. To give an efficient algorithm for finding a maximum independent match-
ing.
We shall prove the min-max duality for independent matchings by showing
the validity of the algorithm.
Let us recall the K¨onig–Egerv´ary theorem (Theorem 2.2.15). It states
that the maximum size of a matching is equal to the minimum size of a
cover, where a cover means a pair (U
+
,U
−
) with U
+
⊆ V
+
and U
−
⊆ V
−
such that ∂
+
a ∈ U
+
or ∂
−
a ∈ U
−
for each a ∈ A, and the size of (U
+
,U
−
)
is defined to be |U
+
| + |U
−
|. We also recall that the inequality
|M|≤|U
+
| + |U
−
| (2.68)
is an obvious relation valid for any matching M and any cover (U
+
,U
−
).
For a cover (U
+
,U
−
) we define the rank of (U
+
,U
−
)by

86 2. Matrix, Graph, and Matroid
ρ
+
(U
+
)+ρ
−
(U
−
),
with reference to the rank functions of the respective matroids M
+
and M
−
.
The obvious relation (2.68) is extended as follows.
Lemma 2.3.26. The inequality
|M|≤ρ
+
(U
+
)+ρ
−
(U
−
) (2.69)
holds true for any independent matching M and any cover (U
+
,U
−
).
Proof. Since (U
+
,U
−
)isacover,M canbeexpressedasM = M
+
∪ M
−
with ∂
+
M
+
⊆ U
+
and ∂
−
M
−
⊆ U
−
. Then
|M
+
| = |∂
+
M
+
| = ρ
+
(∂
+
M
+
) ≤ ρ
+
(U
+
),
|M
−
| = |∂
−
M
−
| = ρ
−
(∂
−
M
−
) ≤ ρ
−
(U
−
),
and the addition of these yields
|M|≤|M
+
| + |M
−
|≤ρ
+
(U
+
)+ρ
−
(U
−
).
The duality in the independent matching problem consists in the assertion
that the equality holds in (2.69) for some M and (U
+
,U
−
). We say (U
+
,U
−
)
is a minimum cover if it attains the minimum in (2.70) below.
Theorem 2.3.27.
max{|M||M : independent matching}
= min{ρ
+
(U
+
)+ρ
−
(U
−
) | (U
+
,U
−
) : cover}. (2.70)
Proof. Lemma 2.3.26 shows max |M|≤min{ρ
+
(U
+
)+ρ
−
(U
−
)}. The equality
is proven later in Lemma 2.3.32 along with the validity of an algorithm for
computing this common value.
It is sometimes convenient to recast Theorem 2.3.27 into different forms.
For U ⊆ V
+
∪ V
−
define the cut capacity of U by
κ(U)=
ρ
+
(V
+
\ U )+ρ
−
(V
−
∩ U )(∃a ∈ A : ∂
+
a ∈ U, ∂
−
a ∈ U)
+∞ (∃a ∈ A : ∂
+
a ∈ U, ∂
−
a ∈ U).
(2.71)
Noting that κ(U ) is finite if and only if (V
+
\ U, V
−
∩ U) is a cover, we can
rewrite Theorem 2.3.27 to
max{|M||M: independent matching} = min{κ(U) | U ⊆ V
+
∪ V
−
}. (2.72)
The function κ to be minimized is submodular in U.
Another form of Theorem 2.3.27 refers to a function Γ :2
V
−
→ 2
V
+
defined by

2.3 Matroid 87
Γ (Y )={u ∈ V
+
|∃v ∈ Y :(u, v) ∈ A},Y⊆ V
−
. (2.73)
Since (U
+
,U
−
) is a cover if and only if Γ (V
−
\ U
−
) ⊆ U
+
, the right-hand
side of (2.70) can be rewritten as
min{ρ
+
(U
+
)+ρ
−
(U
−
) | (U
+
,U
−
): cover}
= min{ρ
+
(Γ (V
−
\ U
−
)) + ρ
−
(U
−
) | U
−
⊆ V
−
}
= min{ρ
+
(Γ (Y )) + ρ
−
(V
−
\ Y ) | Y ⊆ V
−
}.
Therefore Theorem 2.3.27 can be expressed as
max{|M||M: independent matching}
= min{ρ
+
(Γ (Y )) + ρ
−
(V
−
\ Y ) | Y ⊆ V
−
}. (2.74)
Again the function ρ
+
(Γ (Y ))+ρ
−
(V
−
\Y ) to be minimized is submodular in
Y . These alternative expressions (2.71) and (2.74) reveal the submodularity
inherent in the problem at the sacrifice of the symmetry apparent in the
original expression (2.70).
The duality result above implies a number of important consequences.
First of all, if both M
+
and M
−
are free matroids, for which ρ
+
(U
+
)=
|U
+
| and ρ
−
(U
−
)=|U
−
|, the identity (2.70) reduces to the K¨onig–Egerv´ary
theorem (Theorem 2.2.15), whereas (2.74) reduces to the Hall–Ore theorem
(Theorem 2.2.17).
Next, consider the case where M
−
is free (and M
+
is general). The ex-
pression (2.74) in this case takes the form
max{|M||M: matching with ∂
+
M ∈I
+
}
= min{ρ
+
(Γ (Y )) + |V
−
\ Y ||Y ⊆ V
−
}. (2.75)
We call this the Rado–Perfect theorem (cf. Rado [274], Perfect [266]).
Thirdly, the matroid intersection theorem of Edmonds [68, 70] can also
be derived from Theorem 2.3.27.
Theorem 2.3.28 (Matroid intersection theorem). For two matroids
M
i
=(V,I
i
,ρ
i
)(i =1, 2) it holds that
max{|I||I ∈I
1
∩I
2
} = min{ρ
1
(X)+ρ
2
(V \ X) | X ⊆ V }.
Proof.LetV
+
and V
−
be disjoint copies of V and put A = {(v
+
,v
−
) | v ∈ V },
where v
+
∈ V
+
and v
−
∈ V
−
denote the copies of v ∈ V . Consider an
independent matching problem on (V
+
,V
−
; A) with M
+
M
1
and M
−
M
2
. Then the assertion follows from Theorem 2.3.27.
We now turn to the algorithm for computing an independent matching
of the maximum size. The algorithm, starting with the empty matching M,
finds a sequence of independent matchings M with |M| =0, 1, 2, ···with the
88 2. Matrix, Graph, and Matroid
V
+
S
+
∂
+
M
cl
+
(∂
+
M) \ ∂
+
M
V
−
S
−
∂
−
M
cl
−
(∂
−
M) \ ∂
−
M
A
◦
-
s
w
3
-
s
-
3
7
M
◦
A
+
? A
−
6
Fig. 2.9. Auxiliary graph for the independent matching problem
aid of an auxiliary graph
˜
G
M
=(
˜
V,
˜
A; S
+
,S
−
) that has vertex set
˜
V ,arcset
˜
A, entrance vertex set S
+
and exit vertex set S
−
(see Fig. 2.9). The vertex
set
˜
V is given by
˜
V = V
+
∪ V
−
,
whereas S
+
, S
−
and
˜
A are defined with reference to independent matching
M, as follows. The entrance S
+
and the exit S
−
are defined by
S
+
= V
+
\ cl
+
(∂
+
M),S
−
= V
−
\ cl
−
(∂
−
M),
where
cl
+
(X)={v ∈ V
+
| ρ
+
(X ∪{v})=ρ
+
(X)},X⊆ V
+
,
cl
−
(X)={v ∈ V
−
| ρ
−
(X ∪{v})=ρ
−
(X)},X⊆ V
−
,
in accordance with (2.63). The arc set
˜
A consists of four disjoint parts:
˜
A = A
◦
∪ M
◦
∪ A
+
∪ A
−
,
where
A
◦
= {a | a ∈ A} (copy of A),
M
◦
= {a | a ∈ M } (a: reorientation of a),
A
+
= {(u, v) | u ∈ ∂
+
M,v ∈ cl
+
(∂
+
M) \ ∂
+
M,∂
+
M − u + v ∈I
+
},
A
−
= {(v, u) | u ∈ ∂
−
M,v ∈ cl
−
(∂
−
M) \ ∂
−
M,∂
−
M − u + v ∈I
−
}.
Note that
˜
V = V
+
∪ V
−
is partitioned into six disjoint parts with possible
additional connections by M
◦
∪ A
+
∪ A
−
.
2.3 Matroid 89
Example 2.3.29 (Continued from Example 2.3.25). The auxiliary graph
˜
G
M
=(
˜
V,
˜
A; S
+
,S
−
) for the independent matching M = {(x
3
,y
3
), (x
4
,y
4
)}
is depicted in Fig. 2.8(b), where S
+
= {x
1
,x
2
}, S
−
= {y
5
}, A
◦
= A, M
◦
=
{(y
3
,x
3
), (y
4
,x
4
)}, A
+
= ∅,andA
−
= {(y
1
,y
3
), (y
1
,y
4
), (y
2
,y
3
), (y
2
,y
4
)}. 2
The algorithm for the independent matching problem reads as follows.
Algorithm for independent matching problem
Starting with the empty matching M , repeat (i)–(ii) below:
(i) Find a shortest path P (in the number of arcs) from S
+
to S
−
in
˜
G
M
. [Stop if there is no path from S
+
to S
−
.]
(ii) Update M to
M =(M \{a ∈ M | a ∈ P ∩ M
◦
}) ∪ (P ∩ A
◦
).
2
The validity of the algorithm is shown by the lemmas after the example
below.
Example 2.3.30. In the auxiliary graph
˜
G
M
in Fig. 2.8(b), we can take
P = {(x
1
,y
1
), (y
1
,y
4
), (y
4
,x
4
), (x
4
,y
5
)} as a shortest path from S
+
to S
−
.
Then the matching is updated to M = {(x
1
,y
1
), (x
3
,y
3
), (x
4
,y
5
)} in Step (ii)
of the algorithm, and the auxiliary graph changes to
˜
G
M
shown in Fig. 2.10.
The entrance is S
+
= {x
2
}, whereas the exit S
−
is empty, and therefore, no
path exists from S
+
to S
−
. Then the algorithm terminates in Step (i). It will
be shown in Example 2.3.34 that
M is a maximum independent matching. 2
V
+
V
−
A
−
x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4
y
5
+
-
1
-
1
-
-
q
i
6
6
6
?
Fig. 2.10. Auxiliary graph
˜
G
M
(:arcinM;+:vertexinS
+
)
