Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

50 2. Matrix, Graph, and Matroid

Given a sublattice L of 2

, take any maximal ascending chain of L:

(= min L)

⊂

=

⊂

=

⊂

=

···

⊂

=

(= max L), (2.22)

where X

∈L(k =0, 1, ···,b), and put

= X

\ X

k−1

(k =1, ···,b), (2.23)

∞

= V \ X

Then the family of the “intervals” (diﬀerence sets) {V

| k =1, ···,b} is

uniquely determined independently of the choice of the chain. A partial order

 is introduced on {V

| k =1, ···,b} by

 V

⇐⇒ [V

⊆ X ∈L ⇒ V

⊆ X]. (2.24)

In this way, a sublattice L determines a pair of a partition {V

; V

, ···,V

; V

∞

}

of V and a partial order  on {V

, ···,V

}, which will be denoted by

P(L)=({V

; V

, ···,V

; V

∞

}, ). (2.25)

Note that V

= ∅ for k =1, ···,b, whereas V

and V

∞

are distinguished

blocks that can be empty. By (2.24) the indexing of the blocks is consistent

with the partial order in the sense that V

 V

⇒ k ≤ l.

It is often convenient to extend the partial order onto {V

∞

}∪{V

k =1, ···,b} by deﬁning

 V

∞

(∀k). (2.26)

We adopt this convention unless otherwise stated.

Remark 2.2.6. In the above argument we have constructed the partition

; V

, ···,V

; V

∞

} with reference to a particular maximal chain of L. There

is another way of construction of P(L)fromL that refers to join-irreducible

elements instead of a maximal chain. An element Z ∈Lis said to be join-

irreducible if Z = Z



∪ Z



with Z





∈Lmeans Z



= Z or Z



= Z.

Let {Z

| k =1, ···,b} be the family of all the join-irreducible elements

of L distinct from min L.ForeachZ

there exists a unique element of L,

say Y

, that lies immediately below Z

(i.e., Y

⊂ Z

and ∃X ∈Lsuch

that Y

⊂ X ⊂ Z

). Deﬁne V

= Z

\ Y

for k =1, ···,b, V

= min L and

∞

= V \max L. Then {V

; V

, ···,V

; V

∞

} forms a partition of V . A partial

order  is induced on {V

| k =1, ···,b} by [V

 V

⇐⇒ Z

⊆ Z

]. It

is known that this construction coincides with the one deﬁned by (2.23) and

(2.24). 2

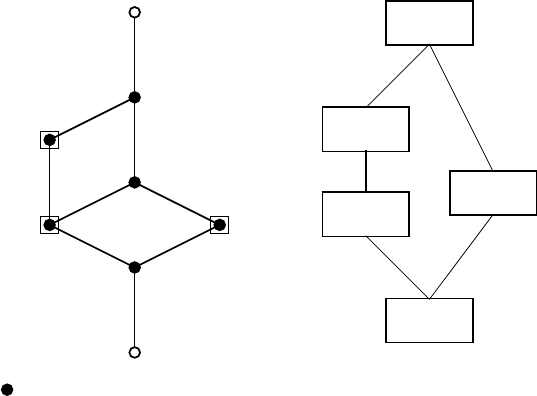
2.2 Graph 51

{1, 2, 3, 4, 5, 6, 7}

{1, 2, 3, 4, 5, 6}

{1, 2, 4, 5, 6}

{1, 2, 3, 4, 5}

{1, 2, 4, 5}{1, 2, 3}

{1, 2}

∅

∈L; 2: join-irreducible =minL

∞

4, 5

1, 2

P(L)

Fig. 2.6. Representation of a sublattice by partially ordered blocks

Example 2.2.7. Let L be a sublattice of 2

indicated by • in Fig. 2.6, where

V = {1, 2, 3, 4, 5, 6, 7}. We have min L = {1, 2} and max L = {1, 2, 3, 4, 5, 6}.

A maximal chain (2.22) with

= {1, 2},X

= {1, 2, 4, 5},X

= {1, 2, 4, 5, 6},X

= {1, 2, 3, 4, 5, 6}

yields V

= {1, 2}, V

= {4, 5}, V

= {6}, V

= {3}, V

∞

= {7}. The partial or-

der P(L) is depicted also in Fig. 2.6. There are three join-irreducible elements

distinct from min L, i.e., Z

= {1, 2, 4, 5}, Z

= {1, 2, 4, 5, 6}, Z

= {1, 2, 3},

indicated by 2 in Fig. 2.6, and the immediately-below elements Y

are

= {1, 2}, Y

= {1, 2, 4, 5}, Y

= {1, 2}. Note that Z

corresponds to

as V

= Z

\ Y

for k =1, 2, 3. 2

Conversely, suppose we are given P =({V

; V

, ···,V

; V

∞

}, ), a pair of

a partition of V with two distinguished subsets V

and V

∞

and a partial order

 on {V

, ···,V

}. Deﬁne L(P) ⊆ 2

L(P)={X ⊆ V | (i) V

⊆ X ⊆ V \ V

∞

;

(ii) X ∩ V

= ∅,V

 V

(1 ≤ k, l ≤ b) ⇒ V

⊆ X}, (2.27)

which implies that X ∈L(P) can be expressed as X =



k∈I∪{0}

for some

I ⊆{1, ···,b}. Then L = L(P) forms a sublattice of 2

with min L = V

and

max L = V \ V

∞

Example 2.2.8. For the P in Fig. 2.6, L(P) consists of six elements: V

{1, 2}, V

∪ V

= {1, 2, 4, 5}, V

∪ V

= {1, 2, 3}, V

∪ V

= {1, 2, 4, 5, 6},

∪ V

= {1, 2, 3, 4, 5}, V

∪ V

= {1, 2, 3, 4, 5, 6}. 2

52 2. Matrix, Graph, and Matroid

Remark 2.2.9. For a partially ordered set P =(S, ) in general, T ⊆ S is

called an order ideal (or simply ideal)if[s  t ∈ T ⇒ s ∈ T ]. The family

of order ideals of P =(S, ) forms a sublattice of 2

(with respect to set

inclusion). With this general terminology, we may say that L(P) is isomorphic

to the lattice of order ideals of ({V

, ···,V

}, ). 2

Birkhoﬀ’s representation theorem states, roughly, that the mappings

Φ : L →P(L) of (2.25) and Ψ : P →L(P) of (2.27) establish a one-to-

one correspondence between the class of sublattices Λ = {L} and that of

partitions Π = {P}. To make the statement more precise we need some

more notation.

We denote by Λ(V ; V

∞

) the collection of the sublattices of 2

that have

as the minimum element and V \V

∞

as the maximum, where V

∩V

∞

= ∅,

i.e.,

Λ(V ; V

∞

)={L | L: sublattice of 2

, min L = V

, max L = V \ V

∞

(2.28)

For L

, L

∈ Λ(V ; V

∞

), L

∧L

will mean the sublattice L

∩L

,and

∨L

the sublattice generated by L

∪L

. The family Λ(V ; V

∞

) forms

a lattice (Λ(V ; V

∞

), ∨, ∧) (in the sense of Remark 2.2.14) with respect to

∧ and ∨ thus deﬁned.

We denote by

Π(V ; V

∞

)={P | P =({V

; V

, ···,V

; V

∞

}, )} (2.29)

the collection of the pairs of a partition {V

; V

, ···,V

; V

∞

} of V with two

distinguished subsets V

and V

∞

and a partial order  on {V

, ···,V

}.A

partial order, denoted also as , can be introduced on Π(V ; V

∞

) with

respect to the reﬁnement relation as follows. For P

=({V

; {V

(1)

}; V

∞

}, 

=({V

; {V

(2)

}; V

∞

}, 

) ∈ Π(V ; V

∞

), we say P

P

if and only if

(i) {V

(1)

} is a reﬁnement of {V

(2)

} as a partition of V \ (V

∪ V

∞

that is, any V

(1)

is contained in some V

(2)

,and

(ii) V

(1)

⊆ V

(2)

, V

(1)

⊆ V

(2)

, V

(1)



(1)

=⇒ V

(2)



(2)

It is easy to see that the partially ordered set (Π(V ; V

∞

), ) thus deﬁned

forms a lattice (Π(V ; V

∞

), ∨, ∧), in which P

∨P

is the ﬁnest common

aggregation of P

and P

∧P

is the coarsest common reﬁnement of

and P

We are now ready to state Birkhoﬀ’s representation theorem.

Theorem 2.2.10 (Birkhoﬀ’s representation theorem). Let V

and V

∞

be disjoint subsets of V . The two families Λ(V ; V

∞

) and Π(V ; V

∞

)

are in one-to-one correspondence to each other through mutually inverse

mappings, Φ : Λ(V ; V

∞

) → Π(V ; V

∞

) and Ψ : Π(V ; V

∞

) →

Λ(V ; V

∞

), deﬁned by Φ : L →P(L) of (2.25) and Ψ : P →L(P) of (2.27),

2.2 Graph 53

respectively. Moreover, for L

, L

∈ Λ(V ; V

∞

) and P

, P

∈ Π(V ; V

∞

)

it holds that

P(L

∧L

)=P(L

) ∨P(L

), P(L

∨L

)=P(L

) ∧P(L

L(P

∧P

)=L(P

) ∨L(P

), L(P

∨P

)=L(P

) ∧L(P

Remark 2.2.11. Theorem 2.2.10 above, referring to two distinguished sub-

sets V

and V

∞

, is slightly diﬀerent from the standard statement of Birkhoﬀ’s

representation theorem. This is for convenience in our subsequent applica-

tions. The essence, however, lies in the case of V

= V

∞

= ∅. 2

Concerning the partial order, we introduce the following additional nota-

tion:

≺ V

⇐⇒ V

 V

and V

= V

; (2.30)

≺· V

⇐⇒



(i) V

≺ V

and

(ii) ∃ V

such that V

≺ V

;

(2.31)

V

 =



≺V

. (2.32)

Example 2.2.12. In Example 2.2.7 (see Fig. 2.6) it holds that V

≺· V

and

≺· V

, while V

≺· V

is not true. We have V

 = ∅, V

 = V

= {1, 2},

V

 = V

∪ V

= {1, 2, 4, 5}, V

 = V

= {1, 2}, V

∞

 = V

∪ V

{1, 2, 3, 4, 5, 6}. Note that V

 = Y

for k =1, 2, 3. 2

So far we have considered how a sublattice L of 2

induces a decompo-

sition of the ground set V into partially ordered blocks. We now go on to

explain how a submodular function f is decomposed into minors on those

blocks if it is modular on L. With reference to the maximal chain (2.22) we

deﬁne f

→ R by

(Y )=f (Y ),Y⊆ V

(Y )=f (X

k−1

∪ Y ) − f(X

k−1

),Y⊆ V

(k =1, ···,b), (2.33)

∞

(Y )=f (X

∪ Y ) − f(X

),Y⊆ V

∞

Obviously, each f

→ R is a submodular function.

The following theorem is sometimes called the Jordan–H¨older-type theo-

rem for submodular functions, after an analogous statement in module theory.

Theorem 2.2.13. Assume that f :2

→ R is submodular and a sublattice

L⊆2

is an f-skeleton, as in (2.19) and (2.20).Letf

(k =1, ···,b) be

deﬁned by (2.33) with reference to a maximal chain of L.Fork =1, ···,b,it

holds that

(Y )=f (V

∪Y ) − f(V

),Y⊆ V

In particular, the family {(V

) | k =1, ···,b} is determined independently

of the choice of a maximal chain.

54 2. Matrix, Graph, and Matroid

Proof. Noting X

k−1

⊇V

, we put W = X

k−1

\V

. Then f

(Y )=f (V

∪

Y ∪ W ) − f (V

∪W ). It follows from the submodularity (2.20) of f that

f(V

∪V

) − f(V

∪Y ) ≥ f(V

∪V

∪ W ) − f(V

∪Y ∪ W ),

f(V

∪Y ) − f(V

) ≥ f(V

∪Y ∪ W ) − f (V

∪W ). (2.34)

Addition of these yields

f(V

∪V

) − f(V

) ≥ f(V

∪V

∪ W ) − f(V

∪W ).

The inequality here is an equality by the modularity of f on L, since V

∪V

V

, V

∪V

∪ W (= X

)andV

∪W (= X

k−1

) all belong to L by

Birkhoﬀ’s representation theorem. Therefore, we have an equality also in

(2.34).

Remark 2.2.14. In abstract terms a lattice is a triple L =(S, ∨, ∧)ofa

nonempty set S and two binary operations ∨ and ∧ on S (called “join” and

“meet” respectively) such that x∨x = x, x∧x = x; x∨y = y ∨x, x∧y = y ∧x;

x∨(y ∨z)=(x ∨y)∨z, x∧(y ∧z)=(x ∧y)∧z; x∧(x∨y)=x, x∨(x∧y)=x

for x, y, z ∈ S. A lattice L =(

S, ∨, ∧) gives rise to a partially ordered set

P =(S, ) with  deﬁned by [x  y ⇐⇒ x ∨y = y]. Such partially ordered

set P =(S, ) enjoys a nice property that for x, y ∈ S there exist a (unique)

minimum element among {z ∈ S | x  z, y  z} (denoted as sup{x, y})and

a (unique) maximum element among {z ∈ S | z  x, z  y} (denoted as

inf{x, y}). Conversely, a partially ordered set P =(S, ) such that sup{x, y}

and inf{x, y} exist for any x, y ∈ S induces a lattice L =(S, ∨, ∧) with ∨ and

∧ deﬁned by x∨y =sup{x, y

} and x∧y =inf{x, y}. A lattice L =(S, ∨, ∧)is

called distributive if x ∧(y ∨z)=(x∧y)∨(x∧z), x∨(y ∧z)=(x∨y)∧(x∨z).

See Birkhoﬀ [12] and Aigner [4] for lattice theory. 2

Notes. The general decomposition principle given as Theorem 2.2.13 is due

to Iri [129], Nakamura [245], and Nakamura–Iri [247]. This is an outcome

of a series of successive generalizations of the concept of principal partitions

for graphs and matroids. See also Kishi–Kajitani [157, 158, 159], Ohtsuki–

Ishizaki–Watanabe [254], Ozawa [260, 262] for principal partitions of graphs,

and Bruno–Weinberg [25], Iri [126], Nakamura–Iri [246], Narayanan–Vartak

[249], Tomizawa [313], Tomizawa–Fujishige [316] for principal partitions of

matroids. In this book we shall make use of this decomposition principle in

a number of places. For example, it underlies the Dulmage–Mendelsohn de-

composition of bipartite graphs (§2.2.3), the min-cut decomposition for inde-

pendent matching problems (§2.3.5), the M-decomposition of graphs (§4.3.2),

and the combinatorial canonical form of layered mixed matrices (§4.4). An-

other general decomposition principle for submodular functions, called the

principal structure, is described in §4.9.2.

2.2 Graph 55

2.2.3 Dulmage–Mendelsohn Decomposition

This section is devoted to a comprehensive account of the Dulmage–Mendel-

sohn decomposition (or the DM-decomposition for short), a unique decom-

position of a bipartite graph with respect to maximum matchings due to

Dulmage–Mendelsohn [63, 64, 65, 66]. A standard reference for matching the-

ory, with emphasis on structures rather than algorithms, is Lov´asz–Plummer

[181].

Let G =(V

−

; A)beabipartite graph with vertex set consisting of

two disjoint parts V

and V

−

and with arc set A, where arcs are directed

from V

to V

−

.ForM (⊆ A) in general, we denote by ∂

M (resp., ∂

−

the set of vertices in V

(resp., V

−

) incident to arcs in M .Alsoweput

∂M = ∂

M ∪ ∂

−

A matching M is a subset of A such that no two arcs in M share a

common vertex incident to them. In other words, M is a matching if and

only if |M| = |∂

M| = |∂

−

M|. A matching of maximum size (cardinality)

is called a maximum matching. The size of a maximum matching in G is

denoted by ν(G). A matching with ∂

M = V

and ∂

−

M = V

−

is called

a perfect matching.AnarcofG is said to be admissible if it is contained in

some maximum matching in G.

A cover is a pair (U

−

)ofU

⊆ V

and U

−

⊆ V

−

such that no arcs

exist between V

and V

−

. The size of a cover (U

−

) is deﬁned

to be |U

| + |U

−

| and a cover of minimum size is called a minimum cover.

We denote by C(G) the family of minimum covers of G.

A duality relation exists between the maximum matchings and the mini-

mum covers.

Theorem 2.2.15 (K¨onig–Egerv´ary). For a bipartite graph we have

max{|M||M : matching} = min{|U

| + |U

−

||(U

−

) : cover}. (2.35)

Proof. This is a special case of Theorem 2.3.27.

To rewrite Theorem 2.2.15 into another form we deﬁne Γ :2

→ 2

−

and γ :2

→ Z by

Γ (X)={v ∈ V

−

|∃u ∈ X :(u, v) ∈ A},X⊆ V

, (2.36)

γ(X)=|Γ (X)|,X⊆ V

, (2.37)

where Γ (X) denotes the set of vertices in V

−

adjacent to some vertex in

X (⊆ V

). In passing we note the following fundamental properties.

Lemma 2.2.16. For X, Y ⊆ V

it holds that

Γ (X ∪ Y )=Γ (X) ∪ Γ (Y ),Γ(X ∩ Y ) ⊆ Γ (X) ∩ Γ (Y ),

γ(X)+γ(Y ) ≥ γ(X ∪ Y )+γ(X ∩ Y ).

56 2. Matrix, Graph, and Matroid

Proof. The ﬁrst claim is easy to verify, while the second follows from

|Γ (X ∪Y )|+|Γ (X ∩Y )|≤|Γ (X)∪Γ (Y )|+|Γ (X)∩Γ (Y )| = |Γ (X)|+|Γ (Y )|.

The second expression of the duality is given in terms of γ as follows.

Theorem 2.2.17 (Hall–Ore).

max{|M||M: matching} = min{γ(X) −|X||X ⊆ V

} + |V

|. (2.38)

Proof. This follows from Theorem 2.2.15 and the fact that (U

−

) is a cover

if and only if Γ (V

\ U

) ⊆ U

−

The function

(X)=γ(X) −|X|,X⊆ V

, (2.39)

appearing in the above identity is called the surplus function in Lov´asz–

Plummer [181], and −p

is the deﬁciency according to Ore [256].

Lemma 2.2.18. The surplus function p

(X) of (2.39) is submodular, i.e.,

(X)+p

(Y ) ≥ p

(X ∪ Y )+p

(X ∩ Y ).

Proof. This is immediate from the submodularity of γ in Lemma 2.2.16.

We may say that the second expression (2.38) for the duality reveals

the submodularity inherent in the problem at the sacriﬁce of the symmetry

apparent in the ﬁrst expression (2.35). On the basis of the submodularity of

we shall derive the DM-decomposition.

Example 2.2.19. The above theorems are illustrated here for the bipartite

graph G =(V

−

; A) in Fig. 2.7, where V

= {u

, ···,u

} and V

−

, ···,v

}. In Theorem 2.2.15,

M = {(u

), (u

)}

is a maximum matching of size |M| =6,and

−

)=({u

}, {v

})

is a minimum cover of size |U

| + |U

−

| = 6. In Theorem 2.2.17, the

surplus function p

(X)=γ(X) −|X| takes the minimum value −1at

X = {u

}, for example, and hence the right-hand side of (2.38) is

equal to 6. It is mentioned in advance that the four subgraphs G

, G

∞

, indicated by vertical broken lines in Fig. 2.7, are the components of the

DM-decomposition to be derived below. 2

2.2 Graph 57

−

∞

−

∞

min. inconsistent

component

(horizontal tail)

consistent components max. inconsistent

component

(vertical tail)

Fig. 2.7. DM-decomposition

The family of subgraphs G

=(V

−

; A

) in the DM-decomposition is

constructed as follows. In view of the minimax relation (2.38) it is natural to

look at the family of the minimizers of surplus function p

min

)={X ⊆ V

| p

(X) ≤ p

(Y ), ∀Y ⊆ V

}, (2.40)

which forms a sublattice of 2

by virtue of the submodularity of p

(cf. Lemma 2.2.18 and Theorem 2.2.5). According to the Jordan–H¨older-

type theorem for submodular functions (§2.2.2), the sublattice L

min

) de-

termines

P(L

min

)) = ({V

; V

, ···,V

; V

∞

}, ), (2.41)

a pair of a partition of V

and a partial order . Here V

= ∅ for k =

1, ···,b, whereas V

and V

∞

are distinguished blocks that can be empty.

In accordance with (2.23) we may assume V

= X

, V

= X

\ X

k−1

(k =1, ···,b), V

∞

= V

\ X

for a maximal chain (X

| k =0, 1, ···,b)of

L = L

min

) (cf. (2.22)). Deﬁne

−

= Γ (X

−

= Γ (X

) \ Γ (X

k−1

)(k =1, ···,b), (2.42)

−

∞

= V

−

\ Γ (X

)

58 2. Matrix, Graph, and Matroid

to obtain a partition (V

−

; V

−

, ···,V

−

; V

−

∞

)ofV

−

, which is determined inde-

pendently of the chosen maximal chain by the following lemma. The notation

V

 is deﬁned in (2.32).

Lemma 2.2.20. V

−

= Γ (V

) \ Γ (V

)(k =1, ···,b).

Proof. Theorem 2.2.13 implies |V

−

| = γ(X

k−1

∪V

) −γ(X

k−1

)=γ(V

∪

) − γ(V

). Since V

−

= Γ (X

k−1

∪ V

) \ Γ (X

k−1

)=Γ (V

) \ Γ (X

k−1

)

and Γ (V

∪V

) \ Γ (V

)=Γ (V

) \ Γ (V

), it follows that |V

−

| =

|Γ (V

) \ Γ (X

k−1

)| = |Γ (V

) \ Γ (V

)|,inwhichΓ(X

k−1

) ⊇ Γ (V

).

Therefore, V

−

= Γ (V

) \ Γ (V

).

The arc set A of G is partitioned accordingly as

A =



∞



k=0



∪

⎛

⎝



k=l

⎞

⎠

= {a ∈ A | ∂

a ∈ V

,∂

−

a ∈ V

−

} (k =0, 1, ···,b,∞),

= {a ∈ A | ∂

a ∈ V

,∂

−

a ∈ V

−

} (k = l; k, l =0, 1, ···,b,∞).

Thus we have obtained the family of subgraphs G

=(V

−

; A

)(k =

0, 1, ···,b,∞), which we call the DM-components. Furthermore we deﬁne

 G

if and only if V

 V

in P(L

min

)), where it is emphasized that

 G

∞

for any k. We call G

the horizontal tail (or the minimal

inconsistent component), G

∞

the vertical tail (or the maximal inconsistent

component) and the others G

(k =1, ···,b)theconsistent components.

Example 2.2.21. For the graph in Fig. 2.7 it can be veriﬁed that

min

)={{u

}, {u

}}.

This yields (2.41) with b =2,V

= {u

}, V

= {u

}, V

= {u

∞

= {u

} and the partial order: V

 V

∞

for k =1, 2. Hence the

four subgraphs G

, G

∞

, indicated by vertical broken lines in Fig. 2.7

with the partial order G

 G

∞

for k =1, 2. The identity in Lemma

2.2.20 for k =2reads{v

} = {v

}\{v

}. 2

The DM-decomposition reveals the structure of a bipartite graph with

respect to maximum matchings and minimum covers, as follows. Recall the

notation ν(G) for the size of a maximum matching in G and C(G) for the

family of minimum covers of G.

Theorem 2.2.22 (Dulmage–Mendelsohn decomposition). Let G

−

; A

)(k =0, 1, ···,b,∞) be the DM-components of a bipartite graph

G =(V

−

; A).

2.2 Graph 59

(1) For 1 ≤ k ≤ b (consistent components): ν(G

)=|V

| = |V

−

C(G

)={(V

, ∅), (∅,V

−

)},andeacha ∈ A

is admissible in G

;

For k =0(horizontal tail): ν(G

)=|V

−

|, |V

−

| < |V

| if V

−

= ∅, C(G

{(∅,V

−

)},andeacha ∈ A

is admissible in G

;

For k = ∞ (vertical tail): ν(G

∞

)=|V

∞

|, |V

∞

| < |V

−

∞

| if V

∞

= ∅, C(G

∞

{(V

∞

, ∅)},andeacha ∈ A

∞

is admissible in G

∞

(2) The partial order  among the components G

is represented by the

existence of arcs:

= ∅ unless G

 G

(1 ≤ k, l ≤ b); (2.43)

= ∅ if G

≺· G

(1 ≤ k, l ≤ b). (2.44)

(3) The minimum covers of G are in one-to-one correspondence with the

order ideals:

C(G)={(



k∈I



k∈I

−

) |{G

| k ∈ I} : order ideal },

where

I = {0, 1, ···,b,∞} \ I, and it is emphasized that 0 ∈ I and ∞ ∈ I if

I corresponds to an order ideal.

(4) M (⊆ A) is a maximum matching of G if and only if M ⊆



∞

k=0

and M ∩ A

is a maximum matching of G

for k =0, 1, ···,b,∞.

Proof. We prove (1), (3), (2) and (4). First note from (2.42) that

= ∅ (k>l). (2.45)

(1) [Size of vertex sets] Since V

∈L

min

), we have

0=p

(∅) ≥ min p

= p

)=γ(V

) −|V

| = |V

−

|−|V

If the equality holds here, then p

(∅) = min p

, which implies V

= ∅ and

therefore V

−

= ∅.Fork =1, ···,b, we have min p

= γ(X

k−1

) −|X

k−1

| =

γ(X

)−|X

|, which means |V

| = |V

−

| by (2.42). If V

∞

= ∅, then p

) >

min p

= p

), i.e., γ(V

)−|V

| >γ(X

)−|X

|. Combination of this with

−

|≥γ(V

), |V

−

∞

| = |V

−

|−γ(X

), |V

∞

| = |V

|−|X

| yields |V

−

∞

| > |V

∞

[Size of maximum matchings] For k =0, 1, ···,b, put Y



l=0

−

and

let G

(k)

be the subgraph of G induced on X

∪Y

. It follows from (2.45) and

Theorem 2.2.17 that

ν(G

(k)

) = min{p

(X) | X ⊆ X

} + |X

| = |Y

which implies ν(G

)=|V

−

| for k =0, 1, ···,b. Since A

∞k

= ∅ for k =

0, 1, ···,b by (2.45) and ν(G

(b)

)=|Y

|,wehave

∞

|≥ν(G

∞

) ≥ ν(G) −|Y

| = min p

+ |V

|−|Y

| = |V

|−|X

| = |V

∞