Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

40 2. Matrix, Graph, and Matroid

2.1.4 Block-triangular Forms

We distinguish two kinds of block-triangular decompositions for matrices.

The one employs a simultaneous permutation of rows and columns and the

other uses two independent permutations.

The ﬁrst block-triangular decomposition is deﬁned for a square matrix

A such that Row(A) and Col(A) have a natural one-to-one correspondence

ψ : Col(A) → Row(A). Let (C

, ···,C

) be a partition of C = Col(A)into

disjoint blocks and (R

, ···,R

) the corresponding partition of R =Row(A)

with R

= ψ(C

)fork =1, ···,b. We say that A is block-triangularized with

respect to (R

, ···,R

) and (C

, ···,C

)if

A[R

]=O for 1 ≤ l<k≤ b.

If this is the case, we can bring A into an explicit upper block-triangular form

A = PAP

in the ordinary sense by using a permutation matrix P , where

it is tacitly assumed that Row(A) = Col(A)={1, 2, ···,n} and ψ(j)=j for

j =1, 2, ···,n. For a general ψ, however,

A = PAP

should be replaced by

A = PAΨ

−1

with another permutation matrix Ψ representing ψ.

A partial order is induced among the blocks {C

| k =1, ···,b} in a

natural manner by the zero/nonzero structure of a block-triangular matrix

A. The partial order  is the reﬂexive and transitive closure of the relation

deﬁned by: C

 C

if A[R

] = O.

Usually we want to ﬁnd a ﬁnest partition of C as well as the corresponding

one of R for which a given matrix A is block-triangularized. This problem

can be treated successfully by means of a graph-theoretic method, as will be

explained in §2.2.1.

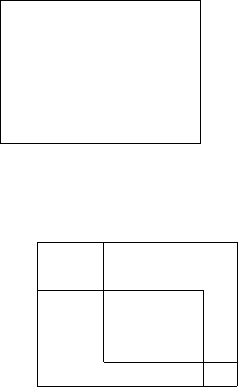
Example 2.1.14. For a 6 × 6 matrix

A =

123456

1 a

2 a

3 a

4 a

5 a

6 a

(2.11)

the ﬁnest block-triangular decomposition is given by

PAP

461253

4 a

6 a

1 a

2 a

5 a

3 a

(2.12)

2.1 Matrix 41

with R

= C

= {4, 6}R

= C

= {1, 2, 5}R

= C

= {3}. 2

The second block-triangular decomposition is deﬁned for a matrix A of

any size, where no correspondence between Col(A)andRow(A) is assumed.

Let (C

; C

, ···,C

; C

∞

) and (R

; R

, ···,R

; R

∞

), where b ≥ 0, be partitions

of C = Col(A)andR =Row(A), respectively, into disjoint blocks such that

| < |C

| or |R

| = |C

| =0,

| = |C

| > 0fork =1, ···,b,

∞

| > |C

∞

| or |R

∞

| = |C

∞

| =0.

(2.13)

We say that A is block-triangularized with respect to (R

; R

, ···,R

; R

∞

)

and (C

; C

, ···,C

; C

∞

)if

A[R

]=O for 0 ≤ l<k≤∞. (2.14)

The submatrices A[R

]andA[R

∞

] are called the horizontal tail and

the vertical tail, respectively. Clearly, if A is block-triangularized in this sense,

we can put it into an explicit upper block-triangular form

A = P

in the

ordinary sense by using certain permutation matrices P

and P

A partial order is induced among the blocks {C

| k =1, ···,b} in a

similar manner by the zero/nonzero structure of a block-triangular matrix

A. The partial order  is the reﬂexive and transitive closure of the relation

deﬁned by: C

 C

if A[R

] = O. It is often convenient to extend the

partial order onto {C

∞

}∪{C

| k =1, ···,b} by deﬁning

 C

∞

(∀k). (2.15)

We adopt this convention unless otherwise stated.

Usually we want to ﬁnd ﬁnest partitions of R and C for which a given

matrix A is block-triangularized. This problem can be treated successfully by

another graph-theoretic method, called the Dulmage–Mendelsohn decompo-

sition, to be explained in §2.2.3.

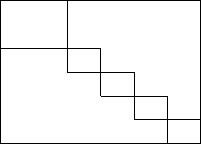
Example 2.1.15. If a transformation of the form

A = P

is applicable

to the matrix A of Example 2.1.14, the ﬁnest block-triangular decomposition

using two permutation matrices is given by

465213



. (2.16)

This consists of ﬁve blocks (R

)=({4



, 6



}, {4, 6}), (R

)=({2



}, {5}),

)=({1



}, {2}), (R

)=({5



}, {1}), (R

)=({3



}, {3}) with

partial order C

 C

, C

 C

. 2

42 2. Matrix, Graph, and Matroid

Remark 2.1.16. The two kinds of decompositions above are closely related

as follows, and this fact seems to cause complications and confusions in the

literature. A considerable number of papers propose or describe a “two-stage

method,” so to speak, that ﬁrst chooses ψ : Col(A) → Row(A) such that

ψ(j),j

=0(j ∈ Col(A)) and then ﬁnds the ﬁnest decomposition of the ﬁrst

kind with respect to the chosen ψ. This amounts to a decomposition under

a transformation P

= PA(Ψ

−1

), where Ψ is the permutation matrix

representing ψ. The following points are emphasized here concerning this

“two-stage method.”

(1) The decomposition produced by the “two-stage method” depends ap-

parently on the choice of ψ. The resulting decomposition, however, is not

aﬀected by the nonuniqueness of ψ, but coincides with the ﬁnest decompo-

sition under a transformation of the form P

(see the algorithm for the

DM-decomposition in §2.2.3). In this sense, the “two-stage method” is fully

justiﬁed from the mathematical point of view.

(2) Still, the “two-stage method” seems to lack in philosophical soundness.

The invariance (or insensitivity) of the resulting decomposition to the choice

of ψ indicates that the “two-stage method” based on PAΨ

−1

should be

recognized in a diﬀerent manner, more intrinsically without reference to ψ.

It can be said that the “two-stage method” is not so much a decomposition

concept as an algorithmic procedure for computing the (ﬁnest) decomposition

under transformations of the form P

. 2

In applications of the second block-triangularization technique it is often

required to impose an additional condition

rank A[R

] = min(|R

|, |C

|)fork =0, 1, ···,b,∞ (2.17)

on the diagonal blocks in the decomposition. If this is the case, A is said

to be properly block-triangularized with respect to (R

; R

, ···,R

; R

∞

)and

; C

, ···,C

; C

∞

). Note that the additional condition (2.17) is of numerical

nature, while the condition (2.14) refers to the zero/nonzero structure only.

Not every matrix has a proper block-triangular form. Consider, for ex-

ample, A =





, which can never be properly block-triangularized for any

partitions. The term-rank is the key concept for the statement of a necessary

and suﬃcient condition for the existence of a proper block-triangular form.

Proposition 2.1.17. A matrix A can be put in a proper block-triangular

form with a suitable choice of partitions of R and C,ifandonlyifrank A =

term-rank A.

Proof. This will be proven later as an immediate corollary of Proposition

2.2.26.

In this book we often encounter questions of the following type:

2.2 Graph 43

A class of matrices and a class of “admissible transformations” for

the class of matrices are speciﬁed. Given a matrix A belonging to the

class, can we transform it to a proper block-triangular matrix

A by

means of an admissible transformation?

By Proposition 2.1.17 this question is equivalent to:

Given a matrix A, can we transform it by means of an admissible

transformation to a matrix

A such that rank

A = term-rank

A ?

The simplest problem of this kind is the case where the class of matrices

comprises all the matrices and any equivalence transformation (

A = S

with nonsingular S

and S

) is admissible. In this case the answer is in the

aﬃrmative and the proper block-triangular matrix

A is given by the rank

normal form of A, i.e.,

A =





with I

denoting the identity matrix of

size r =rankA. Other instances of such questions, more of combinatorial

nature, include: the Dulmage–Mendelsohn decomposition of generic matrices

(§2.2.3), the combinatorial canonical form of layered mixed matrices (§4.4),

the combinatorial canonical form of matrices with respect to pivotal trans-

formations (Remark 4.7.10), and the decomposition of generic partitioned

matrices (§4.8.4).

2.2 Graph

Graphs are convenient tools to represent the structures of matrices and sys-

tems. Decompositions of graphs, when combined with appropriate physical

interpretations, lead to eﬀective decomposition methods for matrices and sys-

tems.

2.2.1 Directed Graph and Bipartite Graph

Let G =(V,A)beadirected graph with vertex set V and arc set A. For an

arc a ∈ A, ∂

a denotes the initial vertex of a, ∂

−

a the terminal vertex of a,

and ∂a = {∂

a, ∂

−

a} the set of vertices incident to a.Foravertexv ∈ V ,

v means the set of arcs going out of v, δ

−

v the set of arcs coming into v,

and δv = δ

v ∪ δ

−

v the set of arcs incident to v.Theincidence matrix of G

is a matrix with row set indexed by V and column set by A such that, for

v ∈ V and a ∈ A, the (v,a)entryisequalto1ifv = ∂

a,to−1ifv = ∂

−

and to 0 otherwise, where, for an arc a with ∂

a = ∂

−

a, the corresponding

column is set to zero.

For V



(⊆ V )the(vertex-)induced subgraph,orthesection graph,onV



is a graph G



=(V



) with A



= {a ∈ A | ∂

a ∈ V



,∂

−

a ∈ V



}. We also

denote G



by G \V



, where V



= V \V



, saying that G



is obtained from G

by deleting the vertices in V



44 2. Matrix, Graph, and Matroid

For two vertices u and v, we say that v is reachable from u on G,which

we denote as u

∗

−→ v, if there exists a directed path from u to v on G.Based

on the reachability we deﬁne an equivalence relation ∼ on V by: u ∼ v ⇐⇒

∗

−→ v and v

∗

−→ u]. In fact it is straightforward to verify (i) [reﬂexivity]

v ∼ v, (ii) [symmetry] u ∼ v ⇒ v ∼ u, and (iii) [transitivity] u ∼ v, v ∼

w ⇒ u ∼ w. Accordingly, the vertex set V is partitioned into equivalence

classes {V

}

, called strongly connected components (or strong components,

in short). Namely, two vertices u and v belong, by deﬁnition, to the same

strong component if and only if u

∗

−→ v and v

∗

−→ u. A partial order  can

be deﬁned on the family {V

}

of strong components by

 V

⇐⇒ v

∗

−→ v

on G for some v

∈ V

and v

∈ V

Each strong component V

determines a vertex-induced subgraph G

)ofG, also called a strong component of G.Thepartial order 

is induced naturally on the family of strong components {G

}

by: G

 G

⇐⇒ V

 V

. The decomposition of G into partially ordered strong compo-

nents {G

}

is referred to as the strong component decomposition of G.An

eﬃcient algorithm of complexity O(|A|) is known for the strong component

decomposition (see Aho–Hopcroft–Ullman [1, 2], Tarjan [310]).

For an n × n matrix A =(A

| i, j =1, ···,n) we can represent the

zero/nonzero pattern of the matrix in terms of a directed graph

G =(V,

with V = {1, ···,n} and

A = {(j, i) | A

=0}. The strong component de-

composition of the graph G corresponds to a (ﬁnest possible) block-triangular

decomposition of the matrix A by means of a simultaneous permutation of

the rows and the columns.

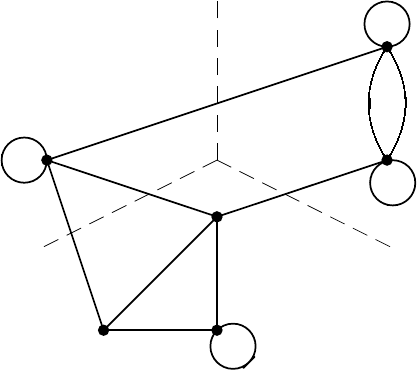
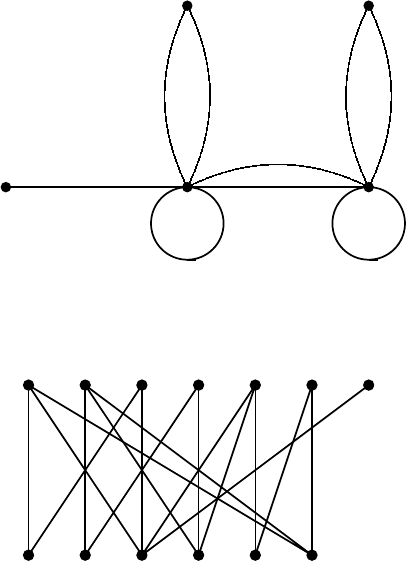
Example 2.2.1. For the matrix A of (2.11) the zero/nonzero structure can

be represented by a directed graph G of Fig. 2.1. The graph has three strong

components, V

= {4, 6}, V

= {1, 2, 5}, V

= {3}, with V

 V

.The

strong component decomposition of G yields a block-triangular form given in

(2.12), where V

corresponds to R

= C

for k =1, 2, 3. 2

In applications of linear algebra it is often crucial to recognize the relevant

transformations associated with a matrix. For example, we can talk of the

Jordan canonical form of A only if A is subject to similarity transformations,

SAS

−1

with nonsingular S. This is the case when A corresponds to a mapping

in a single vector space. If a matrix A corresponds to a mapping between a

pair of diﬀerent vector spaces, it is subject to equivalence transformations,

with nonsingular matrices S

and S

. In this case, it is meaningless

to consider the Jordan canonical form of A, whereas it is still sound to talk

about the rank of A. Consider, for instance, a state-space equation

x =

Ax + Bu for a dynamical system. The matrix A here is subject to similarity

transformations, and B to equivalence transformations. It should be clear

This graph is called the Coates graph in Chen [34].

2.2 Graph 45







Fig. 2.1. Strong component decomposition (Example 2.2.1)

that even if B happens to be square, having as many rows as columns, it is

meaningless to consider the Jordan canonical form of B.

Such distinctions in the nature of matrices should be respected also in the

combinatorial analysis of matrices. As we have observed, the decomposition

of a matrix A through the strong component decomposition of the associated

graph gives the ﬁnest block-triangularization under a transformation of the

form PAP

= PAP

−1

with a permutation matrix P . For this decomposition

method to be applicable it is assumed tacitly that the matrix in question

represents a mapping in a single vector space and is subject to similarity

transformations, so that the structure of the matrix can in turn be represented

by the associated graph deﬁned above.

For a matrix A under equivalence transformations, on the other hand, a

natural transformation of a combinatorial nature will be given by P

with

two permutation matrices P

and P

. For such a matrix there is no reason for

restricting P

to be the inverse of P

, and accordingly the strong component

decomposition does not make much sense. Note that the associated graph

itself is not very meaningful, since the associated graph does not remain

isomorphic when the matrix A changes to P

The structure of such a matrix A (subject to equivalence transformations)

can be better represented by another graph G =(V,

A) with V = Col(A) ∪

Row(A)and

A = {(j, i) | A

=0}. By deﬁnition, each arc has the initial

vertex in Col(A) and the terminal vertex in Row(A), and therefore this graph

is a bipartite graph. Recall that, in general, a graph G =(V,

A) is called a

bipartite graph if the vertex set V can be partitioned into two disjoint parts,

say V

and V

−

,insuchawaythat|∂a ∩V

| = |∂a ∩V

−

| = 1 for all a ∈

46 2. Matrix, Graph, and Matroid

We write G =(V

−

;

A) for a bipartite graph and often assume ∂

a ∈ V

and ∂

−

a ∈ V

−

for a ∈

A. In this notation the bipartite graph associated

with a matrix A is G =(V

−

;

A) with V

= Col(A)andV

−

=Row(A).

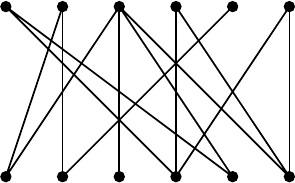
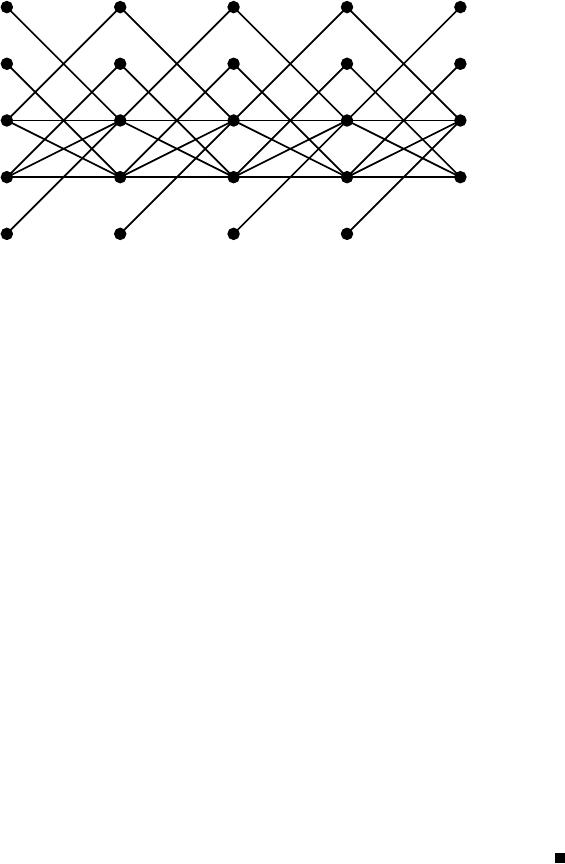
Example 2.2.2. In case the matrix A of (2.11) in Example 2.1.14 represents

a mapping between a pair of diﬀerent vector spaces, the structure of A is

expressed more appropriately by a bipartite graph, shown in Fig. 2.2. 2

−

123456



Fig. 2.2. Bipartite graph representation (Example 2.2.2)

The decomposition under a transformation of the form P

will be

treated in §2.2.3 as the Dulmage–Mendelsohn decomposition.

Remark 2.2.3. For a nonzero entry A

of a matrix A, the associated bi-

partite graph, as deﬁned above, has an arc (j, i) directed from column j to

row i. This convention makes sense when we consider signal-ﬂow graphs and

is often found in the literature of engineering. It is also legitimate to direct

an arc from row i to column j. In this book we use whichever convention is

more convenient in the context. 2

Let us dwell on the distinction of the two kinds of graph representations

by referring to the two kinds of descriptions of dynamical systems introduced

in §1.2.2, namely, the standard form of state-space equations (1.20):

x =

Ax +

and the descriptor form (1.22):

x =

Ax +

Bu.

The matrix

A in the standard form has a natural one-to-one correspondence

between Row(

A) and Col(

A), since the ith equation describes the dynamics

2.2 Graph 47

of the ith variable. The matrix

A in the descriptor form, on the other hand,

has no such natural correspondence between Row(

A) and Col(

A). In other

words, the concept of “diagonal” is meaningful for the matrix

A and not

for the matrix

A. Mathematically,

A is subject to similarity transformations,

−1

,and

A to equivalence transformations, S

Accordingly, the standard form (1.20) is represented by a directed graph

G =(V, A) called the signal-ﬂow graph.

The vertex set V and the arc set A

are deﬁned by

V = X ∪ U, X = {x

, ···,x

},U= {u

, ···,u

A = {(x

) |

=0}∪{(u

) |

=0}.

The natural graphical representation of the descriptor form (1.22), on the

other hand, is the bipartite graph G =(V

−

;

A) associated with the

matrix D(s)=[

A − s

F |

B], where s is an indeterminate. Namely, V

Col(D)=X ∪U stands for the set of variables and V

−

=Row(D) for the set

of equations, say {e

, ···,e

}, and the arcs correspond to the nonvanishing

entries of D(s), i.e.,

A = {(x

) |

=0or

=0}∪{(u

) |

=0}.

It is sometimes convenient to assign weight 1 to arc (x

) with

=0and

weight 0 to the other arcs.

The above distinction between standard form and the descriptor form im-

plies, in particular, that the ﬁnest decomposition of

A is obtained through the

strong component decomposition, whereas that of

A is through the Dulmage–

Mendelsohn decomposition.

For the standard form (1.20) another graph representation is sometimes

useful. For k ≥ 1thedynamic graph of time-span k is deﬁned to be G

∪ U

k−1

) with



t=0

= {x

| i =1, ···,n} (t =0, 1, ···,k),

k−1



t=0

= {u

| j =1, ···,m} (t =0, 1, ···,k−1),

k−1

= {(x

t+1

) |

=0;t =0, 1, ···,k− 1}

∪{(u

t+1

) |

=0;t =0, 1, ···,k− 1}.

Example 2.2.4. The graph representations are illustrated for the mechan-

ical system treated in §1.2.2 (see also Fig. 1.5). The signal-ﬂow graph rep-

resenting the standard form (1.21) and the bipartite graph associated with

The signal-ﬂow graph deﬁned here is diﬀerent from the Mason graph (Chen [34]),

which is sometimes called the signal-ﬂow graph, too.

48 2. Matrix, Graph, and Matroid

u x

? ?



Fig. 2.3. Signal-ﬂow graph of the mechanical system of Fig. 1.5

−

Fig. 2.4. Bipartite graph of the mechanical system of Fig. 1.5

the descriptor form (1.23) are given in Figs. 2.3 and 2.4, respectively. The

dynamic graph of time-span k = 4 for (1.21) is also depicted in Fig. 2.5. 2

2.2.2 Jordan–H¨older-type Theorem for Submodular Functions

We describe here a general decomposition principle of submodular functions,

known as the Jordan–H¨older-type theorem for submodular functions. We

shall make essential use of this general framework in a number of diﬀerent

places in this book. Recall that we have already encountered in §2.1.3 a

typical submodular function, the rank function ρ of (2.6) associated with a

matrix.

Let V be a ﬁnite set, L (= ∅)beasublattice of the boolean lattice 2

X, Y ∈L ⇒ X ∪ Y,X ∩ Y ∈L, (2.18)

2.2 Graph 49

t =0 t =1 t =2 t =3 t =4



Fig. 2.5. Dynamic graph G

of the mechanical system of Fig. 1.5

and f :2

→ R be a submodular function:

f(X)+f(Y ) ≥ f(X ∪ Y )+f(X ∩ Y ),X,Y⊆ V. (2.19)

We say that L is an f-skeleton if, in addition, f is modular on L:

f(X)+f(Y )=f (X ∪Y )+f(X ∩ Y ),X,Y∈L. (2.20)

The decomposition principle applies to a pair of a submodular function

f and an f -skeleton L. In principle, an f-skeleton L can be speciﬁed quite

generally, but in our subsequent applications it is often derived from f itself

as the family of the minimizers, as follows (Ore [257]).

Theorem 2.2.5. For a submodular function f :2

→ R, the family of the

minimizers:

min

(f)={X ⊆ V | f(X) ≤ f(Y ), ∀Y ⊆ V } (2.21)

forms a sublattice of 2

, and moreover it is an f-skeleton.

Proof.Letα denote the minimum value of f.ForX,Y ∈L

min

(f)wehave

2α = f(X)+f(Y ) ≥ f(X ∪ Y )+f(X ∩ Y ) ≥ 2α,

which shows f(X ∪Y )=f(X ∩ Y )=α, i.e., X ∪ Y,X ∩ Y ∈L

min

(f).

First we consider a representation of a sublattice L of 2

, independent of

a submodular function f. This is a fundamental result from lattice theory,

called Birkhoﬀ’s representation theorem, which shows a one-to-one correspon-

dence between sublattices of 2

and pairs of a partition of V into blocks with

a partial order among the blocks. This correspondence is given as follows.