Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

4.2 Rank of Mixed Matrices 151

−



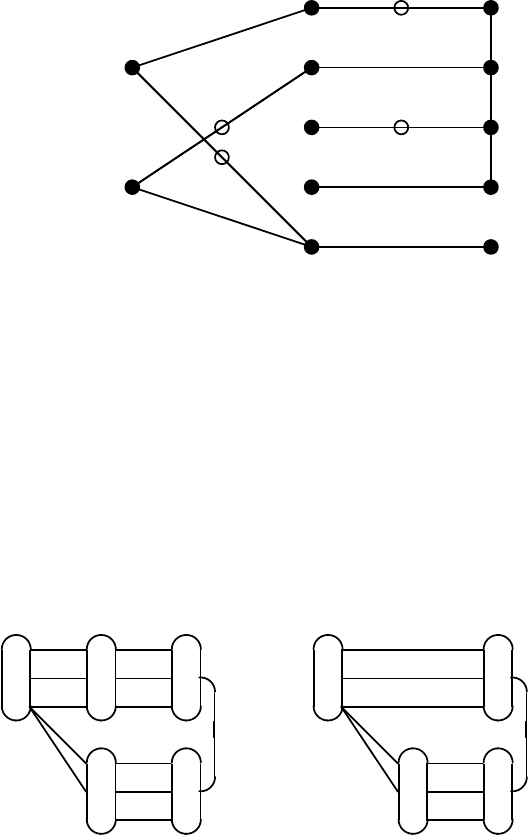
Fig. 4.6. Graph

(4)

(:arcinM; S

= ∅, −:vertexinS

−

)

The vertex set in the general algorithm for

A would consist of three disjoint

parts, say

∪

C, where

corresponds to R  Row(

T ), and

C and

are copies of R ∪ C  Col(

A).

First we exploit the structure of the matrix

Q. In the matroid M(

Q), the

column set corresponding to R is a basis because of the identity submatrix.

Let

be the set of arcs, from

C, connecting the corresponding copies

of R. Then we may take

as the initial independent matching.

C C



⇒

(0)



(0)

+(0)

Initial graph G

(0)

Fig. 4.7. Auxiliary graph for a mixed matrix

Next, by virtue of the diagonal matrix contained in the matrix

T ,the

underlying graph can be simpliﬁed: the arcs in

may be contracted (see

Fig. 4.7). Namely, we may work on a graph with the vertex set consisting of

152 4. Theory and Application of Mixed Matrices

four disjoint parts, R

∪C

∪R

∪C

, where R

=Row(Q), C

= Col(Q),

=Row(T ), and C

= Col(T ). We denote by ϕ

: R ∪ C → R

∪ C

and ϕ

: R ∪ C → R

∪ C

the obvious one-to-one correspondences. The

copies of i ∈ R in R

and R

are written as i

and i

, respectively, that is,

= ϕ

(i)andi

= ϕ

(i). Similarly, we write j

= ϕ

(j)andj

= ϕ

(j).

The initial graph, say G

(0)

, has the arc set E

∗(0)

∪ E

+(0)

, where E

∗(0)

(0)

∪ E

(0)

∪ E

(0)

and

(0)

= {(i

) | i ∈ R},

(0)

= {(j

) | j ∈ C},

(0)

= {(i

) | T

=0,i∈ R, j ∈ C},

+(0)

= {(i

) | Q

=0,i∈ R, j ∈ C}.

The initial matching

turns into an empty matching in the graph G

(0)

and a shortest path L is sought from S

= R

to S

−

= C

in G

(0)

at the

ﬁrst stage of the algorithm.

At a general stage, we maintain I ⊆ R, J ⊆ C and a matching M ⊆

(0)

in (R

; E

(0)

) such that ∂

M ⊆ ϕ

(I), ∂

−

M ⊆ ϕ

(J), and

Q ≡

Q[R \ I,C \ J] is nonsingular. This means that I ∪ (C \ J) is independent

in M(

Q) and (R \ I) ∪ ϕ

−1

(∂

−

M) is independent in M(

T ), and therefore,

R ∪ (C \ J) ∪ ϕ

−1

(∂

−

M) is independent in M(

A). Noting

Q =



R \ II C\ JJ

R \ II

∗

QQ[R \ I,J]

IOI

∗

Q[I,C \ J] Q[I,J]



where I

∗

denotes an identity matrix of appropriate size, let P be the pivotal

transform of Q with pivot

Q. Namely,

P =



R \ IJ

C \ J

−1

Q[R \ I,J]

I −Q[I,C \ J]

−1

Q[I,J] − Q[I,C \ J]

−1

Q[R \ I,J]



where R

≡ Row(P )  I ∪ (C \ J)andC

≡ Col(P )  (R \ I) ∪ J.The

one-to-one correspondence between R

∪C

and R ∪C, which changes with

(I,J), is represented by σ : R

∪ C

→ R ∪ C in the algorithm below. We

start the algorithm with I = R, J = C, M = ∅,andP = Q.

The matching M,thesetsI and J and the structure of P are represented

by a graph G =(V, E) with vertex set V = R

∪ C

∪ R

∪ C

and arc set

E = E

∗

∪ E

, where E

∗

= E

∪ E

∪ M

◦

and

= {(i

) | i ∈ I}∪{(j

) | j ∈ C \J},

= {(i

) | i ∈ R \ I}∪{(j

) | j ∈ J},

4.3 Structural Solvability of Systems of Equations 153

= E

(0)

\ M,

◦

= {a | a ∈ M } (a: reorientation of a),

= {(i

) | P

=0,i∈ (C \ J) ∪ I,j ∈ (R \ I) ∪ J}.

Note that I = {i ∈ R | (i

) ∈ E}, J = {j ∈ C | (j

) ∈ E},and

M = {(i

) | (j

) ∈ E}. The entrance S

and the exit S

−

are deﬁned

= {i

∈ R

| i ∈ I}\∂

−

◦

−

= {j

∈ C

| j ∈ J}\∂

◦

and a shortest path L is sought from S

to S

−

in G.

Algorithm for computing the rank of a mixed matrix A = Q + T

Step 1:

∗

:= {(i

) | i ∈ R}∪{(j

) | j ∈ C}

∪{(i

) | T

=0,i∈ R, j ∈ C};

P [i, j]:=Q

(i ∈ R, j ∈ C); σ(i):=i (i ∈ R ∪ C);

Step 2:

I := {i ∈ R | (i

) ∈ E

∗

}; J := {j ∈ C | (j

) ∈ E

∗

};

◦

:= {(j

) ∈ E

∗

};

:= {i

∈ R

| i ∈ I}\∂

−

◦

; S

−

:= {j

∈ C

| j ∈ J}\∂

◦

;

:= {(i

) | P [σ

−1

(i),σ

−1

(j)] =0,i∈ I ∪(C \ J),j ∈ (R \ I) ∪J};

E := E

∗

∪ E

;

If there exists in G =(V,E) a directed path from S

to S

−

then go to

Step 3; otherwise (including the case where S

= ∅ or S

−

= ∅) stop with

the conclusion that rank A = |M

◦

| + |C \ J|.

Step 3:

Let L (⊆ E) be (the set of arcs on) a shortest path from S

to S

−

(“shortest” in the number of arcs);

∗

:= (E

∗

\ L) ∪{a | a ∈ L ∩ E

∗

}; [Reverse arcs in L ∩ E

∗

]

For all (i

) ∈ L ∩ E

(in the order from S

to S

−

along L)dothe

following:

{h := σ

−1

(i); g := σ

−1

(j); σ(h):=j; σ(g):=i;

w := 1/P [h, g]; P [h, g]:=w;

P [k, g]:=−w × P [k, g](k ∈ R

\{h});

P [h, l]:=w × P [h, l](l ∈ C

\{g});

P [k, l]:=P [k, l] −w × P [k, g] × P [h, l](k ∈ R

\{h},l ∈ C

\{g})

};

Go to Step 2. 2

4.3 Structural Solvability of Systems of Equations

4.3.1 Formulation of Structural Solvability

The unique solvability of a system of linear equations is obviously equivalent

to the nonsingularity of the coeﬃcient matrix. In this section we consider the

154 4. Theory and Application of Mixed Matrices

solvability of a system of linear/nonlinear equations from a combinatorial

structural point of view. A mathematical formalism is given to the intuitive

idea that a system of linear/nonlinear equations has a structure that admits a

unique solution in general. The notion of “structural solvability” in its crude

form seems to have been proposed ﬁrst by Iri–Tsunekawa–Yajima [135] along

with a graph-theoretic criterion for checking it. The present formulation is

due to Iri–Tsunekawa–Murota [134] and Murota–Iri [237, 238].

We consider a system of equations in the following “standard form” with

unknowns x

(j =1, ···,N)andu

(k =1, ···,K), and parameters y

(i =

1, ···,M):

= f

(x, u)(i =1, ···,M),

= g

(x, u)(k =1, ···,K),

(4.27)

where f

(i =1, ···,M)andg

(k =1, ···,K) are assumed to be suﬃciently

smooth real-valued functions. This form is most natural and convenient when

treating a physical/engineering system represented by a set of functional

relations among elementary state variables, where, for arbitrarily given values

of y-variables, the values of x-andu-variables are adjusted so that all the

equations may be satisﬁed.

We are concerned with whether the system (4.27) of equations has a

structure which admits a unique solution. In the following we assume that

M = N, since the number of equations must usually be equal to the number

of unknowns in order for (4.27) to have a unique solution. We denote the

Jacobian matrix of (4.27) with respect to x and u by

J(x, u)=



J[f,x] J[f,u]

J[g,x] J[g, u] − I



, (4.28)

where

J[f,x]=



∂f

∂x



,J[f, u]=



∂f

∂u



J[g,x]=



∂g

∂x



,J[g, u]=



∂g

∂u



Suppose that (4.27) has a solution (x, u)=(

u) for some y =

y.It

follows from the implicit-function theorem (cf., e.g., Spivak [302]) that, if

det J(

u) =0, (4.29)

(4.27) has a unique solution (x, u) around (

u) in accordance with an ar-

bitrary perturbation of y in a neighborhood of

y. It should be noted also

that, from the computational point of view, the condition (4.29) guarantees

the feasibility of a Newton-like iterative method for the numerical solution of

(4.27) with x

(j =1, ···,N)andu

(k =1, ···,K) as unknowns.

The above condition (4.29), however, depends not only on the functional

forms of f

and g

but also on particular values of (

u), which are usually

4.3 Structural Solvability of Systems of Equations 155

not known before we start numerical computation. Furthermore, it is diﬃcult

to distinguish numerically the “exact zero” from a “very small” number due

to the existence of rounding errors. Hence, we will consider an alternative

condition that the Jacobian, as a function in x

(j =1, ···,N)andu

(k =

1, ···,K), does not vanish identically:

det J(x, u) =0.

More precisely, we shall regard the partial derivatives of functions f

and

as elements of a ﬁeld F which is an extension of the rational number ﬁeld

Q. That is, denoting by

D = {∂f

/∂x

,∂f

/∂u

,∂g

/∂x

,∂g

/∂u

i =1, ···M ; j =1, ···,N; k, l =1, ···,K}

the collection of partial derivatives of f

and g

, we adopt

Basic Assumption: D⊆F .

This assumption is literally valid, for example, if f

and g

are rational func-

tions of x

(j =1, ···,N)andu

(l =1, ···,K), in which case the ﬁeld of all

rational functions in x

(j =1, ···,N)andu

(l =1, ···,K) may be taken as

the ﬁeld F . We say that the system (4.27) of equations is structurally solvable

if the Jacobian matrix J(x, u) of (4.28), as a matrix over F , is nonsingular,

i.e., if

det J(x, u) =0 inF . (4.30)

The structural solvability condition (4.30) implies a one-to-one correspon-

dence between x

(j =1, ···,N)andy

(i =1, ···,M) in the following (struc-

tural) sense. The submatrix J[g, u] −I is term-nonsingular under a plausible

assumption that the diagonal entries of J[g,u] are distinct from one (see

§2.1.3 for the terminology of “term-nonsingular”). This means further that

J[g,u]−I is likely to be nonsingular. Then, by the implicit-function theorem,

the second subsystem of (4.27):

= g

(x, u)(k =1, ···,K) (4.31)

can be solved for u

= u

(x)(k =1, ···,K). (4.32)

Substitution of (4.32) into the ﬁrst subsystem of (4.27) yields a system of

equations

= f

(x, u(x)) (i =1, ···,M) (4.33)

in unknowns x

(j =1, ···,N). The Jacobian matrix J[y,x] of (4.33) is given

J[y,x]=J[f,x] − J[f,u](J[g, u] − I)

−1

J[g,x] (4.34)

156 4. Theory and Application of Mixed Matrices

as long as J[g, u] − I is nonsingular. In fact, this expression is derived from

the relations among the diﬀerentials of (4.27):

dy = J[f,x]dx + J[f,u]du,

du = J[g, x]dx + J[g, u]du

through elimination of du. If (4.27) is structurally solvable (4.30), the Ja-

cobian matrix J[y,x] above is nonsingular by a formula in matrix algebra

(cf. Proposition 2.1.7):

det





= det D · det[A − BD

−1

(where A and D are square matrices and det D = 0), and hence x

(j =

1, ···,N)andy

(i =1, ···,M) are in one-to-one correspondence, at least

locally.

In the following we consider combinatorial characterizations of the struc-

tural solvability under two diﬀerent generality assumptions, GA1 and GA2

introduced in §3.1.1. Generality assumption GA1 leads to a graph-theoretic

method in §4.3.2, whereas GA2 to a matroid-theoretic method in §4.3.3.

4.3.2 Graphical Conditions for Structural Solvability

The structure of a system of equations in the standard form (4.27) can be

expressed in terms of a graph with vertices corresponding to variables (i.e.,

unknowns (x, u) and parameters y) and arcs representing the existence of

the explicit direct functional dependence. To be concrete, we consider the

vertex set X ∪ U ∪ Y , where X = {x

, ···,x

}, U = {u

, ···,u

} and

Y = {y

, ···,y

}. The functional dependence y

= f

(x, u) is expressed by a

set of arcs coming into y

from those x

and u

which eﬀectively appear in f

In a similar manner, the functional dependence u

= g

(x, u) is expressed

by a set of arcs coming into u

from x

and u

appearing eﬀectively in g

The graph thus obtained may be regarded as a kind of signal-ﬂow graph

representing the causal relation among variables, or the ﬂow of information

in the system. This graph is called the representation graph (Iri–Tsunekawa–

Murota [134]) of the system of equations. When it is acyclic, it is also called

the computational graph (Bauer [10]), in which emphasis is laid on the aspect

that it represents the order of successive function evaluations according to

which the values of y

are computed from those of x

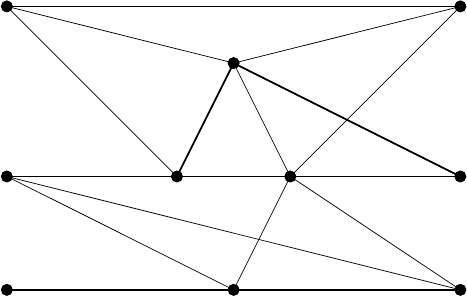
Example 4.3.1. For a system of equations:

= f

),u

= g

= f

),u

= g

= f

),u

= g

the representation graph G is shown in Fig. 4.8. 2

4.3 Structural Solvability of Systems of Equations 157





s



Fig. 4.8. Representation graph of Example 4.3.1 (linking arcs in thick lines)

By the deﬁnition of the sets X, Y ,andU, the representation graph of a

system of equations in the standard form satisﬁes the following properties:

i) Each vertex x

∈ X has no in-coming arcs, and vice versa.

ii)Each vertex y

∈ Y has no out-going arcs. (Some of the vertices of U may

possibly have no out-going arcs.)

Note that the representation graph expresses nothing more than the existence

of functional dependence among variables, concrete functional forms being

disregarded.

The objective of this section is to translate the structural solvability con-

dition (4.30) into a condition on the representation graph under the generality

assumption

GA1: The nonvanishing elements of D are algebraically independent

over Q

about the collection D of the partial derivatives. Structural solvability under

GA1 is equivalent to generic solvability when the nonvanishing elements of D

are regarded as independent parameters. It is also noted that the structural

solvability under GA1 is equivalent to the nonsingularity of J[y, x] of (4.34)

since GA1 guarantees the nonsingularity of J[g, u] − I.

The generality assumption GA1 can be partly justiﬁed as follows. When

the system of equations describes a physical system, the functions f

and g

represent element characteristics which cannot be free from noises and/or

errors. Hence the nonvanishing partial derivatives of f

and g

, even when

they are constant (i.e., when the functions are linear), are so “general” that

they do not satisfy any polynomial relation with integer coeﬃcients. Thus

we are led to GA1. It is admitted at the same time that concrete numerical

158 4. Theory and Application of Mixed Matrices

data stored in a computer with a ﬁnite number of digits cannot satisfy this

assumption in the rigorous mathematical sense, and that the assumption is

sometimes too stringent to be satisﬁed in practical problems.

The structural solvability (4.30) under GA1 is equivalent to the existence

of a Menger-type perfect linking in G as follows (see §2.2.4 for Menger-type

linkings).

Theorem 4.3.2. A system of equations in the standard form (4.27) is struc-

turally solvable under GA1 if and only if there exists on the representation

graph G =(X ∪ U ∪ Y,A; X, Y ) a Menger-type perfect linking from X to Y .

Proof. First, the diagonal entries of J[g,u]−I are distinct from zero by GA1.

Next, J(x, u) of (4.28) is nonsingular if and only if it is term-nonsingular. This

follows from Proposition 2.1.12 when combined with a simple observation

that multiplication of the last K rows of J(x, u) by algebraically independent

numbers yields a matrix with algebraically independent nonvanishing entries.

It remains to show the equivalence of the term-nonsingularity of J(x, u)

and the existence of a Menger-type perfect linking.

Suppose J(x, u) is term-nonsingular. Fix a bijection π : X ∪ U → Y ∪U

such that J

π(v)v

=0(∀ v ∈ X ∪ U). Obviously M = N.Foreachx

∈ X

(1 ≤ j ≤ N) determine a sequence u

, ···,u

m(j)

∈ U and y

σ(j)

∈ Y by

π(x

)=u

, π(u

)=u

, ···, π(u

m(j)−1

)=u

m(j)

,andπ(u

m(j)

)=y

σ(j)

Such sequences for diﬀerent j have no vertex in common, and the collection

of such sequences gives a Menger-type perfect linking in G.

Conversely, suppose that there exists a Menger-type perfect linking in G,

and let U



(⊆ U ) denote the set of u-vertices lying on the linking. Then M =

N and the linking gives a bijection π : X ∪U



→ Y ∪U



such that J

π(v)v

=0

(∀ v ∈ X ∪U



). The bijection π can be extended to π : X ∪U → Y ∪U such

that J

π(v)v

=0(∀ v ∈ X ∪U) by deﬁning π(v)=v for v ∈ U \U



. This shows

the term-nonsingularity of J(x, u).

The above criterion for structural solvability was put to practical use in a

chemical process simulator developed in Japan in the seventies (IJUSE [121],

ITPA [118], ITPA–IJUSE [119, 120], and Sebastian–Noble–Thambynayagam–

Wood [293]). See Murota [204, §10] for an account of other graph-theoretic

techniques employed there.

Example 4.3.3. Recall the system of equations in Example 4.3.1. As shown

in Fig. 4.8, there exists a Menger-type perfect linking: x

→ y

, x

→ u

→

→ y

, x

→ u

→ y

, in the representation graph G. Hence, by Theorem

4.3.2, this system of equations is structurally solvable under GA1. 2

Next we turn to another example which is not structurally solvable. This

motivates us to look at minimum separators as the reason for the failure of

structural solvability.

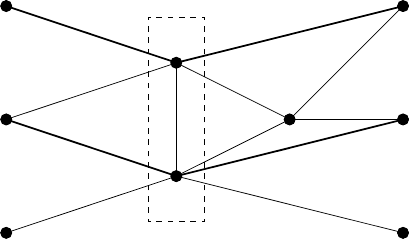
4.3 Structural Solvability of Systems of Equations 159

Example 4.3.4. A system of equations:

= f

),u

= g

= f

),u

= g

= f

),u

= g

)

has the representation graph G shown in Fig. 4.9, in which there is a path

from any x

(j =1, 2, 3) to any y

(i =1, 2, 3). However, since a maximum

linking from X = {x

} to Y = {y

} is of size 2, not a perfect

linking, Theorem 4.3.2 reveals that this system is not structurally solvable.

min separator





Fig. 4.9. Representation graph of Example 4.3.4 (linking arcs in thick lines)

An intuitive interpretation of this fact would be that three degrees of

freedom at the entrance X are reduced to two of the intermediate variables,

and u

, and, as a result, it is not possible in general to adjust the values

of x

and x

so as to make y

and y

equal to arbitrarily prescribed

values.

More precisely, we may say the following, referring to Menger’s theorem

(Theorem 2.2.31). In the representation graph G of Fig. 4.9, {u

} is a

minimum separator of (X, Y ). The cardinality of a minimum separator in

the representation graph of the system (4.27) of equations may be inter-

preted as the eﬀective degrees of freedom of the system. Thus, for a system

of equations not necessarily structurally solvable, a minimum separator in its

representation graph can reveal where the inconsistency comes from. 2

Remark 4.3.5. Theorem 4.3.2, as well as the argument in Example 4.3.4,

suggests that some meaningful decomposition of a system of equations

should be obtained through a decomposition of its representation graph

based on maximum linkings and minimum separators. In fact, this idea has

been worked out by Murota [196, 205] and the obtained decomposition is

160 4. Theory and Application of Mixed Matrices

named “Menger-decomposition” (or “M-decomposition” for short). The M-

decomposition is constructed as follows. The linking problem can be formu-

lated as a network ﬂow problem (see §2.2.4), maximum linkings corresponding

to maximum ﬂows and minimum separators to minimum cuts. On the other

hand, the submodularity (2.52) of the cut capacity function of a network

leads to a canonical decomposition with respect to minimum cuts, accord-

ing to the Jordan–H¨older-type theorem for submodular functions explained

in §2.2.2. The essence of the M-decomposition is a straightforward combina-

tion of these two results. See Murota [196, 197, 205] as well as Murota [204,

§8, §11] for details about M-decomposition and its application to systems of

equations, and van der Woude [327] for its application to control theoretic

problems. Another decomposition of the representation graph is also proposed

by Iri–Tsunekawa–Yajima [135], and is named “L-decomposition” by Iri–

Tsunekawa–Murota [134]; see also Murota [204, §8, §11] for L-decomposition.

Remark 4.3.6. The structural solvability for systems of equations with de-

grees of freedom is discussed by Sugihara [304, 305]. This is closely related

to the combinatorial analysis of rigidity in statics, as expounded in Recski

[277]. 2

4.3.3 Matroidal Conditions for Structural Solvability

With the aid of the combinatorial characterizations of the rank of a mixed

matrix, we can deal with the structural solvability of a system of equations

(4.27) under more realistic generality assumptions such as

GA2: Those elements of D which do not belong to the rational num-

ber ﬁeld Q are algebraically independent over Q,and

GA3: Those elements of D which do not belong to the real number

ﬁeld R are algebraically independent over R,

where D denotes the collection of the partial derivatives of the equations.

Recall that the generality assumptions GA2 and GA3 have been introduced

in §3.1.1 on the basis of the physical observation on the two kinds of numbers.

To be speciﬁc, we assume GA2 (and GA3 can be treated similarly). The

set D is divided into two parts, D = Q∪T with Q = D∩Q and T = D\Q.

Accordingly, the Jacobian matrix A = J(x, u) is expressed as A = Q + T ,

which is, by GA2, a mixed matrix with respect to (Q, F ).

The following theorem gives a matroid-theoretic criterion for the struc-

tural solvability of the system (4.27) of equations under the realistic assump-

tion GA2.

Theorem 4.3.7. Let the Jacobian matrix A

= J(x, u) of (4.28) be decom-

posed into two parts, A = Q + T , such that Q is a matrix over Q and the

nonzero entries of T do not belong to Q. Then the system (4.27) of equations