Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

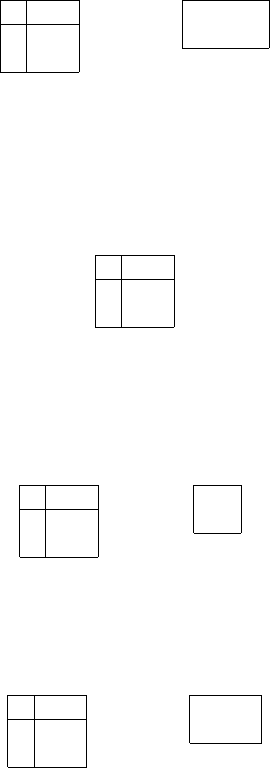
4.4 Combinatorial Canonical Form of LM-matrices 201

1/41/2

−3/21

The CCF

has two square blocks C

= {x

} and C

= {x

} with no

order relation between them.

The transformation matrix S = S

is not a matrix over Z. However, a

transformation over Z can be constructed easily by putting S = S

=4· S

which yields another CCF:

16 32

It is noted, however, that the transformation with S = S

is not invertible

over Z since S

, with det S

= 16, is not unimodular.

Restricting S to a unimodular matrix over Z, we may take S =

S below

(with det

S =1)totransformA to a block-triangular matrix

A, where

A =

1 36

816

S =

−11

−32

The order relation of the blocks in

A is given by: C

= {x

}C

= {x

This matrix

A has the same diagonal blocks as yet another CCF of A,

below, that is obtained with S = S

, where

816

1/81/4

−32

A concrete instance of Theorem 4.4.19 with D being a ring of univariate

polynomials will be given in Example 6.3.10.

Notes. The content of Theorem 4.4.19 was observed by Murota [216] in the

case where D is a ring of univariate polynomials, whereas the present form

is found in Murota [218]. We consider some variants and extensions of the

CCF later in §4.6, §4.7, §4.8, and §4.9. It is mentioned in this connection that

a hierarchical decomposition of discrete systems possessing group symmetry

has been investigated in Murota [217] by combining the combinatorial method

for the CCF and the conventional group representation theory.

202 4. Theory and Application of Mixed Matrices

4.5 Irreducibility of LM-matrices

In this section we investigate into a concept of irreducibility for LM-matrices.

Most of the results below are natural extensions of those concerning DM-

irreducibility (or full indecomposability) for generic matrices treated in §2.2.3.

4.5.1 Theorems on LM-irreducibility

With respect to the LM-admissible transformation (4.35) we can deﬁne a

concept of irreducibility for LM-matrices. An LM-matrix A ∈ LM(K, F )is

deﬁned to be LM-reducible if it can be decomposed into smaller submatri-

ces by means of the LM-admissible transformation (4.35). Otherwise, A is

called LM-irreducible. In other words, A is LM-reducible if there exists a

DM-reducible matrix A



that is LM-equivalent to A,andA is LM-irreducible

if any LM-matrix A



that is LM-equivalent to A is DM-irreducible. An LM-

irreducible matrix is DM-irreducible, and not conversely. Note that an LM-

matrix A is LM-irreducible if Row(A)=∅ or Col(A)=∅, since the whole

matrix A is a (horizontal or vertical) tail. On the other hand, a zero ma-

trix A = O with Row(A) = ∅ and Col(A) = ∅ is LM-reducible, since it can

be decomposed into the horizontal tail with (R

)=(∅, Col(A)) and the

vertical tail with (R

∞

)=(Row(A), ∅).

From Theorem 4.4.4 we obtain the following characterization of LM-

irreducibility in terms of the lattice L

min

(p) of the minimizers of the LM-

surplus function p. This is a kind of “dual” characterization of the LM-

irreducibility in contrast to the “primal” characterization (deﬁnition) in terms

of the indecomposability with respect to the LM-admissible transformation.

Theorem 4.5.1. Let A ∈ LM(K, F ) be an LM-matrix.

(a) In case |R| < |C|: A is LM-irreducible ⇐⇒ L

min

(p)={C};

(b) In case |R| = |C|: A is LM-irreducible ⇐⇒ L

min

(p)={∅,C};

min

(p)={∅}. 2

The validity of the algorithm for CCF in §4.4.4 yields a characterization

of the LM-irreducibility in terms of the graph

G used in the algorithm. In

particular, we mention the case of square LM-matrices.

Theorem 4.5.2. A square LM-matrix A is LM-irreducible (and hence non-

singular) if and only if in Step 4 of the algorithm of §4.4.4 both V

and V

∞

are empty and R

∪ C is contained in a single strong component of

G. 2

The following theorem refers to the rank of submatrices of an LM-

irreducible matrix. This is an extension of Theorem 2.2.24 for a generic ma-

trix.

Theorem 4.5.3. Let A ∈ LM(K, F ) be LM-irreducible.

(a) In case |R| < |C|: rank A[R, C \{j}]=|R| (∀j ∈ C);

(b) In case |R| = |C|: rank A[R\{i},C\{j}]=|R|−1(∀i ∈ R, ∀j ∈ C);

]=|C| (∀i ∈ R).

4.5 Irreducibility of LM-matrices 203

Proof. See the proof of (B4) of Theorem 4.4.4.

As immediate corollaries we obtain the following properties of a nonsin-

gular irreducible LM-matrix. We regard the determinant of A ∈ LM(K, F )

as a polynomial in T (=set of nonzero entries of T ) with coeﬃcients from the

ground ﬁeld K, that is, det A ∈ K[T ].

Theorem 4.5.4. Let A ∈ LM(K, F ) be nonsingular and LM-irreducible.

(1) A

−1

is completely dense, i.e., (A

−1

)

=0for all (j, i).

(2) Each element of T appears in det A.

Proof. (1) This follows from Theorem 4.5.3(b), since (A

−1

)

= det A[R \

{i},C \{j}]/ det A.

(2) If t ∈Tis the (i, j)entryofA, det A contains t·det A[R\{i},C\{j}] =

0, which is not cancelled out.

The converse of Theorem 4.5.4(1) does not hold true. That is, a nonsin-

gular LM-matrix A may possibly be LM-reducible even if (A

−1

)

= 0 for all

(j, i).

Example 4.5.5. Consider an LM-matrix A and its CCF

A =





1 −10

10 1

0 t

A =

1 −10

0 11

0 t

where t

and t

are indeterminates over K = Q. Every minor of order two of

A is nonsingular and hence (A

−1

)

= 0 for all (j, i). But A is LM-reducible

with its CCF splitting into two blocks. 2

The following theorem (Murota [207]) states that the combinatorial irre-

ducibility (namely LM-irreducibility) is essentially equivalent to the algebraic

irreducibility of the determinant as a polynomial in T over K.Thisisanex-

tension of Theorem 2.2.28 for a generic matrix.

Theorem 4.5.6. Let A ∈ LM(K, F ) be a nonsingular LM-matrix. If A is

LM-irreducible, det A is irreducible as a polynomial in T over K. Conversely,

if det A is an irreducible polynomial, then in the CCF of A, there is at most

one diagonal block that contains elements of T and all the other diagonal

blocks are 1 × 1 matrices over K.

Proof. The proof of the ﬁrst half is given later in §4.5.2. The second half

follows easily from Theorem 4.4.4 and Theorem 4.5.4(2).

Remark 4.5.7. If two square LM-matrices A

(k)

∈ LM(K, F )(k =1, 2) are

LM-equivalent, being connected by an LM-admissible transformation (4.35),

they have an identical determinant up to a constant factor: det A

(1)

= c ·

204 4. Theory and Application of Mixed Matrices

det A

(2)

with c ∈ K

∗

= K \{0}. The converse of this statement, however, is

not true. For example, the LM-matrices

(1)

⎡

⎢

⎣

100110

010011

001101

00t

0 t

00t

⎤

⎥

⎦

(2)

⎡

⎢

⎣

100101

010110

001011

00t

0 t

00t

⎤

⎥

⎦

have an identical determinant (both being LM-irreducible). However, these

matrices are not LM-equivalent. Thus, the determinant does not characterize

the LM-equivalence.

In this connection we mention an observation of Ryser [285] that a fully

indecomposable (DM-irreducible) matrix is determined, up to scaling, by the

determinant of its formal incidence matrix. To be precise, let B

(k)

(k =1, 2)

be two fully indecomposable square matrices over K,andM

(k)

(k =1, 2) be

the formal incidence matrices deﬁned by M

(k)

= B

(k)

with indeterminates

. Then, B

(1)

= D

(2)

for some nonsingular diagonal matrices D

and

over K if and only if det M

(1)

= c · det M

(2)

for some c ∈ K

∗

. 2

A minor (=subdeterminant) of A ∈ LM(K, F ) is also a polynomial in T

over K.Letd

(T ) ∈ K[T ] denote the kth determinantal divisor of A, i.e.,

the greatest common divisor of all minors of order k as polynomials in T over

K. Note that d

(T ) ∈ K

∗

means d

(T ) is a nonzero “constant” free from

any variables in T .

Theorem 4.5.8. Let A ∈ LM(K, F ) be LM-irreducible.

(a) In case |R| < |C|: d

(T ) ∈ K

∗

for k =1, ···, |R|;

(b) In case |R| = |C|: d

(T ) ∈ K

∗

for k =1, ···, |R|−1;

(T ) ∈ K

∗

for k =1, ···, |C|.

Proof. We prove (b), while (a) and (c) can be proven similarly. By the Laplace

expansion (Proposition 2.1.2), d

k−1

(T ) divides d

(T )fork =2, ···, |R|−1,

and hence it suﬃces to show that d

(T ) is free from any t ∈T for k = |R|−1.

Suppose t appears at position (i, j). It follows from Theorem 4.5.3(b) that

δ ≡ det A[R\{i},C\{j}] = 0. Obviously δ does not contain t, and, a fortiori,

(T ) does not contain t, since d

(T ) is a divisor of δ.

The determinantal divisors of a general (possibly reducible) LM-matrix

can be expressed in terms of the CCF as follows.

Theorem 4.5.9. Let d

(T ) denote the kth determinantal divisor of A ∈

LM(K, F ) for k =1, ···,r,wherer =rankA.Thend

(T ) ∈ K

∗

for k =

1, ···,r − 1,andd

(T ) is decomposed into irreducible factors (in the ring

K[T ])as

4.5 Irreducibility of LM-matrices 205

(T )=α ·



l∈I

det

A[R

where α ∈ K

∗

,and

A[R

](l ∈ I) are the LM-irreducible square blocks in

the CCF of A that contain an element of T .

Proof. The claim follows from Theorems 4.4.4, 4.5.6 and 4.5.8.

4.5.2 Proof of the Irreducibility of Determinant

The proof of the ﬁrst half of Theorem 4.5.6 is given below. Assume that A is

nonsingular and LM-irreducible, and suppose that det A is decomposed as

det A = f

· f

(4.70)

with f

∈ K[T ] \K (k =1, 2). For k =1, 2, we denote by T

(= ∅) the subset

of T consisting of the indeterminates appearing in f

. Since det A is linear in

each element of T and since Theorem 4.5.4(2) holds, {T

, T

} is a nontrivial

partition of T , i.e., T

∩T

= ∅ and T

∪T

= T .Put

= {i ∈ R

| T

∈T

},C

= {j ∈ C | T

∈T

} (k =1, 2). (4.71)

Then we have R

= ∅, C

= ∅ (k =1, 2) and

T 1

∩ R

T 2

= ∅,R

T 1

∪ R

T 2

= R

∩ C

= ∅,C

∪ C

= C,

where the ﬁrst and the third relation are obvious, the second relation R

T 1

∪

T 2

= R

is due to the fact that the matrix T has no zero row because of

the nonsingularity of A, and the last relation C

∪ C

= C follows from the

fact that the matrix T has no zero column because of the LM-irreducibility

of A.

We claim that

T [R

T 1

]=O, T[R

T 2

]=O. (4.72)

For, if there exist i ∈ R

T 1

, j ∈ C

such that T

= 0, the indeterminate T

must appear in det A by Theorem 4.5.4(2), which contradicts the deﬁnitions

(4.71). Thus we have the ﬁrst assertion in (4.72). Similarly for the second.

By Lemma 4.2.1 there exists

J ⊆ C such that

Q[R

J]andT[R

,C \

J] are nonsingular. (4.73)

Fixing arbitrarily a one-to-one correspondence ϕ : R

→

J and choosing

S = Q[R

−1

in the LM-admissible transformation (4.35), we may assume

Q[R

J]=I. It should be noted here that the LM-admissible transformation

changes the determinant only by a factor in K \{0}.Put

206 4. Theory and Application of Mixed Matrices

= C

J (k =1, 2),C

= C

T 1

∪ C

T 2

(= C \

J),

= C

∩

J (k =1, 2),C

= C

∪ C

J),

= ϕ

−1

)(k =1, 2),R

= R

∪ R

(k =1, 2).

Then we see that T [R

] is nonsingular for k =1, 2 by (4.72) and (4.73),

and that |R

| = |C

| (k =1, 2) and R

∪ R

= R

. Hence we can extend

ϕ : R

→

J to ϕ : R → C in such a way that

i,ϕ(i)

=1 (i ∈ R

),T

i,ϕ(i)

=0 (i ∈ R

). (4.74)

Hence we have the following picture of the matrix A:

T 1

T 2

IQ[R

T 1

] OQ[R

T 2

]

T 1

T [R

T 1

] T [R

T 1

] OO

OQ[R

T 1

] IQ[R

T 2

]

T 2

OOT[R

T 2

] T [R

T 2

]

, (4.75)

where the diagonal submatrices are all nonsingular.

By the Laplace expansion of (4.75) with respect to the rows of R

T 2

obtain

det A =



⊆C

± det A[R \ R

T 2

,C \ J

] · det T [R

T 2

in which no similar terms appear among the nonvanishing terms for distinct

. Consider the particular term for J

= C

T 2

. By (4.74), det T [R

T 2

]

contains a nonvanishing term τ =

i∈R

T 2

i,ϕ(i)

, which, multiplied by

det A[R \ R

T 2

,C \ C

T 2

] = det A[R

], appears in det A. In other words,

if we think of det A as a polynomial in T

over K[T

], the coeﬃcient of τ is

equal to det A[R

]. On the other hand, since the term τ is contained in

of (4.70) with a nonzero coeﬃcient, say c



,inK, the coeﬃcient of τ in

· f

is equal to c



· f

∈ K[T

]. Therefore, we see that

= c

· det A[R

],c

∈ K.

Similarly we have

= c

· det A[R

],c

∈ K.

That is,

det A = c

· det A[R

] · det A[R

] = det A[R

] · det A[R

(4.76)

where we see c

= 1 from (4.75).

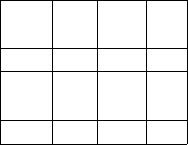
4.5 Irreducibility of LM-matrices 207

Remark 4.5.10. Before proceeding further, we explain our intuition be-

hind the rigorous arguments that follow, though this remark is not neces-

sary from the mathematical logical point of view. Since A is LM-irreducible,

Q[R

T 1

] is not a zero matrix (see (4.75)), that is, there exist i

∈ R

∈ C

T 1

such that Q

= 0. Since A[R \{i

},C \{j

}] is nonsingular by

Theorem 4.5.3, we have a nonzero term :



i∈R

i,σ(i)



i∈R

i,σ(i)



i∈R

i,σ(i)

involving Q

in the usual expansion of det A into the sum of products,

where σ : R → C is a permutation, or a one-to-one correspondence such that

σ(i

)=j

One might be tempted to claim that this contradicts (4.76) based on the

observation that this term cannot appear on the right hand side of (4.76)

since i

∈ R

⊆ R

and σ(i

)=j

∈ C

T 1

⊆ C

. This reasoning, however, is

not rigorous since this term may or may not be cancelled out by similar terms.

In fact, the following example of an LM-irreducible matrix demonstrates that

such cancellation does occur:

A =

T 1

T 2

10 1 00 1

01 1 00 1

T 1

00 0

001

(∗)

10 1

00 1 01 1

T 2

00 0 y

where R

= {r

},R

T 1

= {r

},R

= {r

},R

T 2

= {r

}; C

},C

T 1

= {c

},C

= {c

},C

T 2

= {c

}. If we choose i

= r

= c

(at the position (∗)), we have

det A[R \{i

},C \{j

}]=x

+ x

These terms, however, are cancelled out and do not appear in

det A = −x

− x

+ x

A rather sophisticated argument below is to overcome this complication in

deriving a contradiction. It is noted in passing that det A aboveisanirre-

ducible polynomial in Q[x

]. 2

Associated with the matrix A of (4.75), we deﬁne, with reference to ϕ,a

graph G =(V, E) with vertex set V = R

∪C and arc set E = E

∪E

where

208 4. Theory and Application of Mixed Matrices

= {(ϕ(i),j) | i ∈ R

,j ∈ C

=0},

= {(i, j) | i ∈ R

,j ∈ C, T

=0},

= {(ϕ(i),i) | i ∈ R

Note that by (4.72) there exist no arcs between R

T 1

and C

nor between

T 2

and C

. Also note that (i) a vertex of R

has exactly one in-coming arc,

which is in E

, (ii) a vertex of C

has exactly one out-going arc, which is

in E

, (iii) the arcs coming into a vertex of C

belong to E

, whereas the

arcs going out of a vertex of C

belong to E

The graph G is strongly connected by the LM-irreducibility of A and

Theorem 4.5.2, since G is obtained from the graph

G in the CCF-algorithm

of §4.4.4 by identifying the corresponding copies of C. Therefore, there exists

in G a directed simple cycle which contains both a vertex of C

and a vertex

of C

. Choose such a directed cycle H having the minimum number of arcs,

and let E

(⊆ E) denote the set of arcs in H. We index the arcs of E

∩E

in such a way that

, ···,e

(= e

)

appear in this order along the cycle H, ∂

∈ C

,and∂

−

∈ C

, where,

for e ∈ E in general, ∂

e and ∂

−

e designate the initial and terminal vertices.

Note here that {∂

,∂

−

}⊆C (= C

∪C

)forr =1, ···,msince e

∈ E

From among the arcs e

, ···,e

, we pick up those which connect from

to C

or from C

to C

, and denote them as

ˆe

, ˆe

, ···, ˆe

ˆm

(= ˆe

where they are indexed again along H and ˆe

ˆm

= e

; put

E = {ˆe

, ···, ˆe

ˆm

Note that ˆm is even and that



∂

ˆe

∈ C

,∂

−

ˆe

∈ C

(s: odd)

∂

ˆe

∈ C

,∂

−

ˆe

∈ C

(s: even)

for s =1, ···, ˆm.

With reference to ϕ we deﬁne

= ϕ

−1

(∂

) ∈ R

= ∂

−

r−1

∈ C

(r =1, ···,m),

= ϕ

−1

(∂

ˆe

) ∈ R

= ∂

−

ˆe

s−1

∈ C

(s =1, ···, ˆm).

This means

=(ϕ(i

),j

r+1

)(r =1, ···,m), ˆe

=(ϕ(

s+1

)(s =1, ···, ˆm).

Here and below the indices r and s are to be understood with modulo m and

modulo ˆm, respectively. We further deﬁne r(s)(s =1, ···, ˆm)byj

r(s)

(s =1, ···, ˆm), and put

4.5 Irreducibility of LM-matrices 209

−

= {i

| r(s) ≤ r ≤ r(s +1)− 1} (s =1, ···, ˆm),

−

= ϕ(I

−

)={ϕ(i

) | r(s) ≤ r ≤ r(s +1)− 1} (s =1, ···, ˆm),

= {j

| r(s) ≤ r ≤ r(s +1)− 1} (s =1, ···, ˆm);

−



s:odd

−



s:even

−

∪

−

= {i

| r =1, ···,m},

−



s:odd

−



s:even

−

∪

−

= {ϕ(i

) | r =1, ···,m},



s:odd



s:even

∪

= {j

| r =1, ···,m}.

Then the end vertices of the arcs of E

∩ E

are partitioned into ˆm (≥

2) disjoint “blocks” J

∪ J

−

(s =1, ···, ˆm), the consecutive blocks being

connected by arcs of

E. Also note that



⊆ C

T 1

−

⊆ C

(s: odd)

⊆ C

T 2

−

⊆ C

(s: even)

for s =1, ···, ˆm.

With the notation above we now make key observations which are con-

sequences of the minimality of the chosen cycle H. The ﬁrst observation is

that

e ∈ E

,ϕ(i

)=∂

e ∈ J

−



= ∂

−

e ∈ J

⇒ r



≤ r +1. (4.77)

This states that there are no “forward” arcs in E

within each block. The

second observation is that

e ∈ E

,∂

e ∈ J

−

,∂

−

e ∈ J



,s= s



⇒ e ∈

E. (4.78)

This says that the arcs of

E are the only arcs of E

connecting vertices in

diﬀerent blocks.

In terms of matrix Q, (4.77) and (4.78) are rephrased as follows:



=0,i

∈ I

−



∈ J

⇒ r



≤ r +1, (4.79)

that is, Q[I

−

] is in a lower-left Hessenberg form for each s;and



=0,i

∈ I

−



∈ J



,s= s



⇒



= s + 1 (mod ˆm)



= r +1=r(s



) (mod m).

(4.80)

In addition, we have

r+1

=0 (r =1, ···,m) (4.81)

that correspond to arcs of E

∩ E

In the case of ˆm = 4, for example, Q[

−

] looks as follows

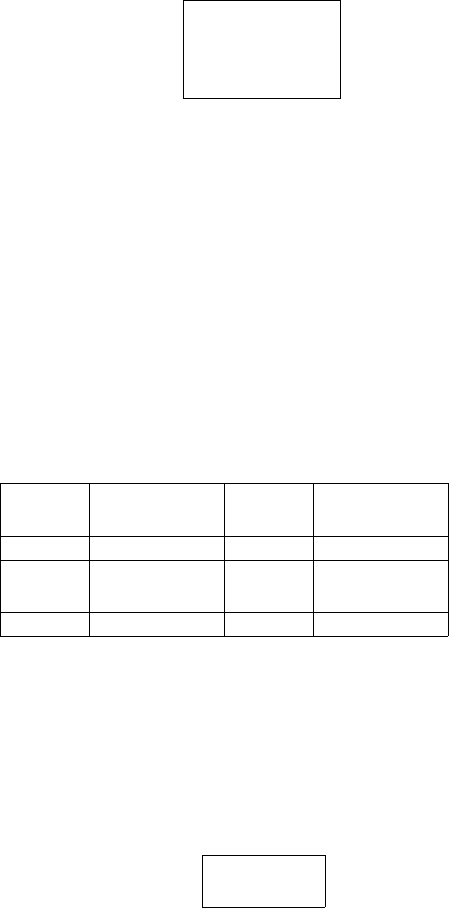
210 4. Theory and Application of Mixed Matrices

−

OOH

−

OOH

, (4.82)

where the rows are indexed by i

, ···,i

in this order, and the columns

by j

, ···,j

in this order. For each s =1, ···, ˆm, H

= Q[I

−

]is

a lower-left Hessenberg matrix with nonzero upper subdiagonal entries that

correspond to arcs in (E

∩E

) \

E,andD

s,s+1

= Q[I

−

s+1

] contains the

only one nonzero entry in the lower-left corner that corresponds to an arc in

It follows from (4.79), (4.80), and (4.81) (also (4.82)) that

det Q[

−

] = det Q[

−

] · det Q[

−

]+α (4.83)

with α = ±

r=1

r+1

=0.

By introducing

−

,and

(k =1, 2) into (4.75), we obtain the

following more detailed picture:

A =

T 1

T 2

−

IOQ[∗] Q[∗] OO Q[∗] Q[∗]

−

OI Q[∗] Q[1, 1] OO Q[∗] Q[1, 2]

T 1

T [∗] T [#] T [#] T [∗] OO OO

OO Q[∗] Q[∗] IOQ[∗] Q[∗]

−

OO Q[∗] Q[2, 1] OI Q[∗] Q[2, 2]

T 2

OO OOT [∗] T[#] T [#] T [∗]

← C

∗

→←C

∗

→

. (4.84)

Here

= R

−

= C

−

= C

(k =1, 2);

T [∗]andT [#] are each a submatrix of T ; Q[∗] denotes a submatrix of Q,and

Q[k, l]=Q[

−

](k, l =1, 2) are submatrices of Q[

−

] of (4.82), i.e.,

−

Q[1, 1] Q[1, 2]

−

Q[2, 1] Q[2, 2]

. (4.85)

Since H is a directed cycle and E

is a matching in G,

∗

=(E

\ E

) ∪{(j, i) | i ∈ R

,j ∈ C, (i, j) ∈ E

∩ E

}

is again a matching of size |R

|. This implies that T [R

∗

]isnonsin-

gular for k =1, 2, where