Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.

92
O
2
A
1
2
a
2
≡
f
O
a
A
2
A
1
A
1
1
r
i
2
f
Å
i
1
≡
O
1
p
2
p
1
Î
A
1
2
i
2
A
1
a
a
2
r
f
Å
A
O
2
i
A
2
f
Å
A
1
1
i
1
≡
O
1
A
1
r
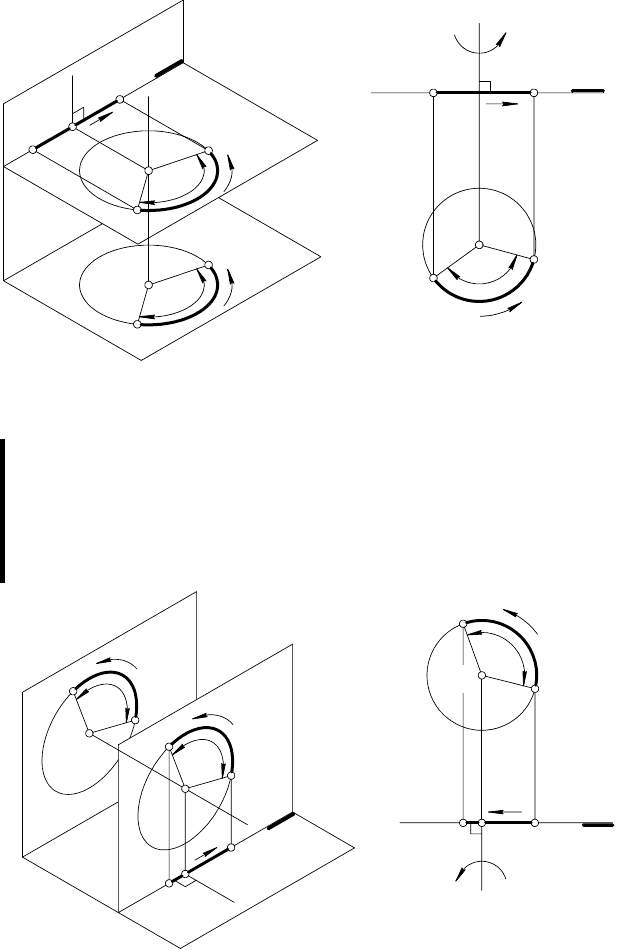
а б
Рис. 98
Из приведенных рассуждений следует:
при вращении точки вокруг фронтально проецирующей оси ее
фронтальная проекция перемещается по окружности с центром
в точке, являющейся проекцией оси вращения, радиусом равным
расстоянию между фронтальными проекциями точки и оси;
а горизонтальная проекция — по прямой, перпендикулярной гори-
зонтальной проекции оси вращения.
Î
A
1
2
i
1
A
1
b
b
1
A
O
1
i
A
2
A
1
1
i
2
≡
O
2
A
1
f Å
f Å
p
1
p
2
x
O
1
A
1
1
b
1
≡
h
O
b
A
1
A
2
A
1
2
i
1
i
2
≡
O
2
f Å
а б
Рис. 99
93
Зная, как перемещаются проекции точки при ее вращении
вокруг прямой, перпендикулярной плоскости проекций, осуще-
ствляют перемещение любой геометрической фигуры из задан-
ного положения в частное путем ее поворота вокруг оси i ⊥ π
1
(или π
2
).
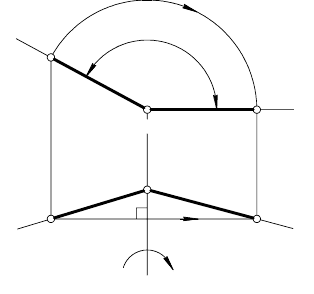
ЗАДАЧА. Отрезок прямой
общего положения перевести в
положение горизонтали
(рис. 100).
РЕШЕНИЕ.
1.
Сначала выбирают ось вра-
щения i. В данном примере
ось ( i ⊥ π
2
) проходит через
один из концов отрезка
[ АВ ] — точку В.
2.
Определяют угол и направ-
ление вращения. Величина
угла ϕ° определится после
того, как будет проведена
прямая
1
2
m
, занимающая положение фронтальной проекции
горизонтали (
1
2
m
⊥ B
1
B
2
).
3.
При переводе отрезка [ АВ ] в новое положение [ А
1
В
1
] во-
круг оси i ⊥ π
2
достаточно повернуть только точку А. При
вращении точки А ее фронтальная проекция А
2
перемещает-
ся по дуге окружности О (O
2
, r) до положения
1
2
1
2
mA ∈
, а го-
ризонтальная А
1
— по прямой, перпендикулярной i
1
, до пе-
ресечения с линией связи (
1
1
1
2
AA
). Точка В ∈ i и не меняет
своего положения:
2
1
2
BB ≡
и
1
1
1
BB ≡
. Отрезок [ А
1
В
1
] ⊂
⊂ m
1
|| π
1
занимает положение горизонтали.
7.2. ВРАЩЕНИЕ ВОКРУГ ОСИ ПАРАЛЛЕЛЬНОЙ ПЛОСКОСТИ
ПРОЕКЦИЙ (ВРАЩЕНИЕ ВОКРУГ ЛИНИИ УРОВНЯ)
Способ вращения вокруг линии уровня позволяет повернуть
заданную плоскую геометрическую фигуру до положения, па-
раллельного одной из плоскостей проекций, и получить проек-
Рис. 100
O
1
B
1
2
≡
B
2
≡
i
2
≡
O
2
A
1
2
A
2
m
2
m
1
B
1
1
≡
B
1
m
1
1
A
1
1
A
1
i
1
m
1
2
f
Å
r
94
цию фигуры на параллельную плоскость, конгруэнтную самой
фигуре (оригиналу). Это позволяет определить все метрические
характеристики оригинала.
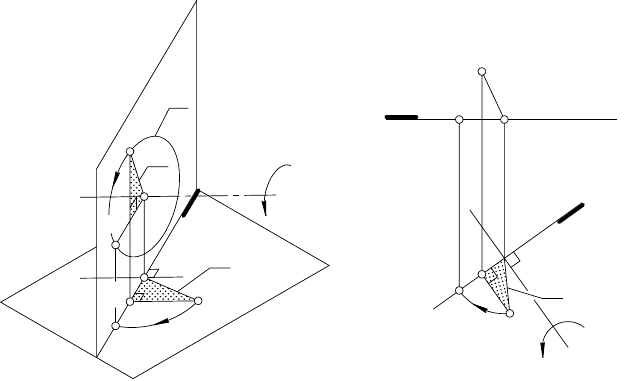
При вращении оригинала вокруг принадлежащей ему гори-
зонтали, его переводят в положение, параллельное π
1
; вращая
оригинал вокруг его фронтали — в положение, параллельное π
2
.
Каждая точка в плоскости оригинала при вращении пере-
мещается по окружности, расположенной в плоскости перпен-
дикулярной оси вращения. Центр окружности вращения нахо-
дится на оси вращения, а ее радиус равен расстоянию от оси до
вращающейся точки. Если за ось вращения взять горизонталь h
(рис. 101), то окружность с, являющаяся траекторией движения
точки, на π
1
спроецируется в отрезок прямой, перпендикуляр-
ной горизонтальной проекции h
1
горизонтали h. На плос-
кость π
2
окружность c проецируется в эллипс, построение кото-
рого можно не выполнять. На эпюре (рис. 102) изображают
плоскость вращения точки (плоскость β), не изображая при
этом проекции окружности с. Чтобы определить новое положе-
ние точки при повороте ее вокруг горизонтали h, находят центр
вращения (точка О) и радиус вращения R (см. рис. 101
и 102).
p
1
O
2
A
1
2
a
2
A
2
h
2
h
1
A
1
A
0
A
1
1
R
2
2
O
1
2
A
h
1
A
1
1
A
0
A
1
O
1
A
1
O
R
b
2
c
R
1
1
1
b
1
≡
h
0
b
h
2
b
1
≡
h
0
b
Рис. 101 Рис. 102
Центр вращения находится в точке О пересечения оси вра-
щения h с плоскостью β. Радиус вращения определяют с помо-
щью прямоугольного треугольника
0
1
1
AAO
(см. 2.7.). Новое по-

95
ложение
1
1
A
точки А после ее поворота до плоскости
α (А
1
, h) || π
1
находится в конце отрезка [О
1
1
1
A
] = R, отложенно-
го от центра О
1
на следе плоскости h
0
β
≡ β
1
. Точку
1
1
A
можно
построить с помощью дуги
1
10
AA
окружности О (О
1
, R
).
Проанализировав приведенные рассуждения, определяют
порядок построений, необходимых для поворота одной точки
оригинала вокруг линии уровня:
1)
провести ось вращения (горизонталь или фронталь) принад-
лежащую плоскости оригинала;
2)
через заданную точку провести плоскость ее вращения, пер-
пендикулярно оси;
3)
найти центр вращения, как точку пересечения оси с плоско-
стью вращения точки;
4)
определить величину радиуса вращения с помощью прямо-
угольного треугольника;
5)
в плоскости вращения точки, от центра вращения, отло-
жить отрезок, равный величине радиуса вращения.
Рассмотрим пример.
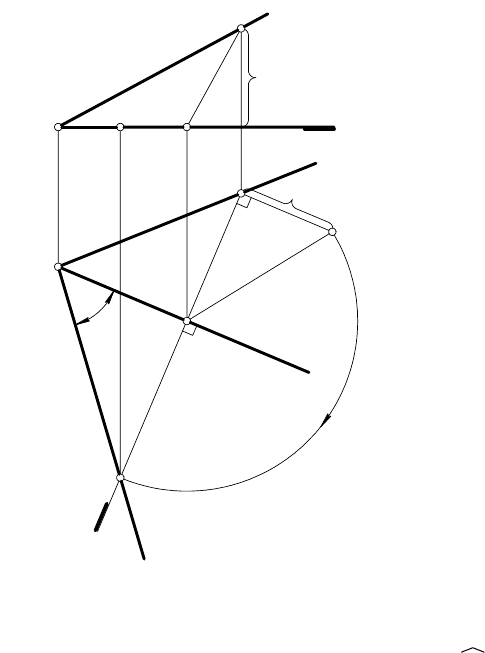
ЗАДАЧА. Определить величину угла между прямыми
m и h (рис. 103).
РЕШЕНИЕ.
1.
За ось вращения выбирают горизонталь h. Она принадлежит
плоскости α (m I h);
2.
На второй стороне угла выбирают произвольную точку В и
вращают ее вокруг оси h до положения плоскости
δ
|| π
1
. Для
осуществления поворота проводят плоскость вращения точ-
ки В
: В ⊂ β ⊥ h;
3.
Определяют центр вращения О = β I h;
4.
Находят величину радиуса вращения R = [O
1
В
0
] с помощью
прямоугольника О
1
В
1
В
0
. В
U
О
1
В
1
В
0
катет О
1
В
1
— горизон-
тальная проекция радиуса R = |ОВ |, а катет В
1
В
0
равен
∆z = z
B
— z
0
. Гипотенуза [О
1
В
0
] равна радиусу вращения R
точки В.
5.
В плоскости β от точки О откладывают отрезок [
1
1
OB
] = R.
На эпюре проекцию
1
1
B
точки после поворота определяют с
помощью дуги
1
10
BB
окружности О (О
1
, R ):
h
0
β
I О (О
1
, R) =
1
1
B
.
96
O
1
B
1
B
1
1
O
2
h
0
b
≡
b
1
A
1
2
≡
A
2
B
0
B
1
2
h
2
≡
h
1
2
≡
d
2
≡
m
1
2
B
2
h
1
≡
h
1
1
f
Å
m
2
D
z = z
b
- z
0
R
D
z = z
b
- z
0
m
1
A
1
1
≡
A
1
m
1
1
Рис. 103
6.
Точка А остается неподвижной (А ∈ h). Поэтому
1
1
A
≡ А
1
. Со-
единяя точки
1
1
A
и
1
1
B
, получают величину угла ϕ° = mh.
97
Лекция 8 (2 часа)
Тема «Кривые линии»
План
1.
Основные понятия и определения.
2.
Пространственные кривые и свойства их проекций
3.
Конические сечения. Ортогональные проекции окружности.
8.1. ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Линии занимают в начертательной геометрии особое поло-
жение. С их помощью решают многие научные и инженерные
задачи. Линии используют при конструировании поверхностей
различных технических форм.
Представляя линию траекторией перемещения точки, ее
рассматривают как непрерывное множество всех принадлежа-
щих ей точек.
Линии подразделяют на алгебраические (окружность, эл-
липс, парабола, гипербола и др
.), если в декартовой системе
осей координат они определяются алгебраическими уравнения-
ми, и трансцендентные (синусоида, спираль Архимеда, циклои-
да и др.), если их уравнения трансцендентны.
Линии, все точки которых не принадлежат одной плоскости,
называют пространственными.
Порядок алгебраической пространственной кривой опреде-
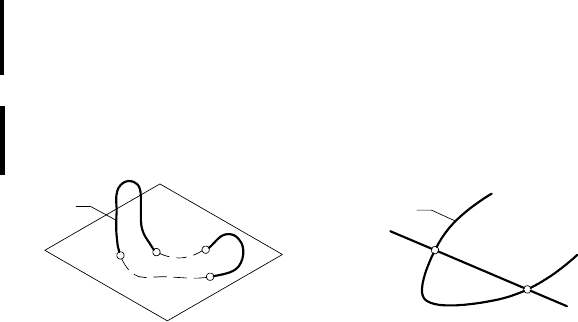
ляется числом ее точек пересечения с плоскостью (рис. 104, а).
Линии, у
которых все точки принадлежат одной плоскости, на-
зывают плоскими.
p
1
l
1
2
3
4
l
1
2
a
а б
Рис. 104
98
Порядок плоской алгебраической кривой определяется чис-
лом ее точек пересечения с прямой линией (рис. 104, б).
8.2. КРИВЫЕ И СВОЙСТВА ИХ ПРОЕКЦИЙ
Для определения ортогональных проекций кривой строят
проекции ряда ее точек и соединяют между собой их одно-
именные проекции в той последовательности, в какой они рас-
полагались на оригинале. Проекциями плоских и пространст-
венных кривых являются линии плоские (см. 1.5., свойство 1а).
При задании кривой ее проекциями показывают хотя бы одну
точку, принадлежащую
кривой (рис. 105), так как по проекциям
l
1
и l
2
нельзя судить о форме кривой l.
l
2
l
1
A
2
A
1
À
2
Ñ
2
1
2
Ì
2
B
2
B
1
M
1
1
1
≡
2
1
Ñ
1
A
1
2
2
Рис. 105 Рис. 106
По двум ортогональным проекциям кривой не всегда сразу
можно ответить на вопрос о том, какой кривой (плоской или
пространственной) соответствуют данные проекции. Чтобы оп-
ределить, плоская или пространственная кривая линия задана
на эпюре, выясняют, принадлежат ли все точки кривой одной
плоскости: если принадлежат — кривая плоская, если не все
принадлежат — пространственная. Заданная
на рис. 106
кривая l — пространственная, так как точка М, взятая на кри-
вой, не принадлежит плоскости, определяемой точками А, В и С
этой кривой. Плоскую кривую образуют движением точки в
плоскости.
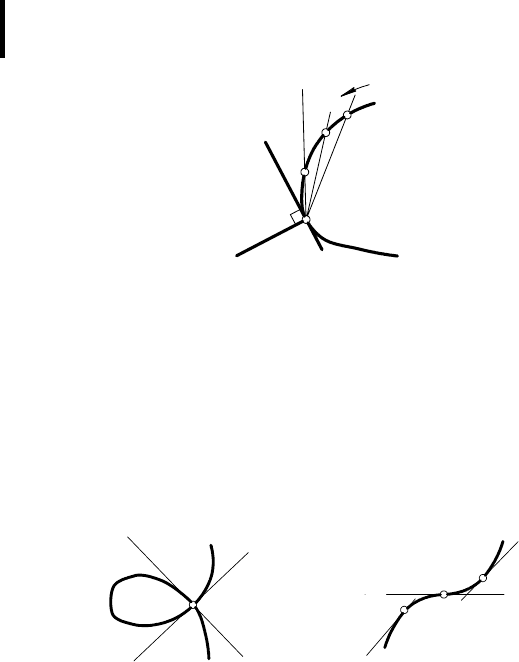
Каждому положению точки на кривой соответствует, вообще
говоря, единственная касательная к этой кривой. Эта касатель-
ная t
M
есть предельное положение секущей ММ
1
(рис. 107) при
перемещении точки М
1
по кривой l до ее совпадения с точкой
М.
Предельное положение секущей в точке М называется касатель-
ной к кривой l в точке М.
99
Прямая n
М
, перпендикулярная к касательной t
M
в данной точке
М, называется нормалью кривой l в данной точке M.
M
1
2
1
M
n
M
t
M
l
Рис. 107
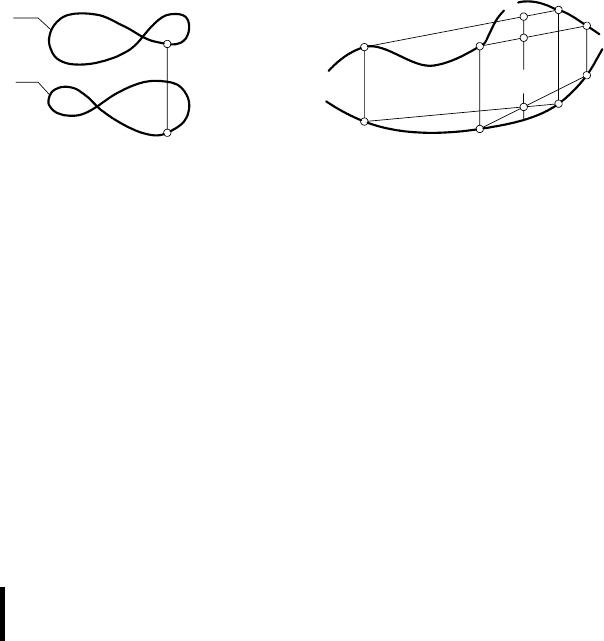
Кривые имеют обыкновенные и особые точки. На рис. 108, а
представлен пример такой особой точки М, где кривая сама се-
бя пересекает. Такую точку называют узловой точкой кривой.
Точка перегиба N на кривой l получается там (рис. 108, б),
где касательная, огибающая кривую, меняет свое направление.
Точка перегиба N не является особой, но
в этой точке кривая
имеет особую касательную t
N
.
M
t
M
1
l
t
M
2
K
N
t
N
а б
Рис. 108
При построении ортогональных проекций кривых необхо-
димо знать те свойства этих кривых, которые сохраняются при
проецировании.
Свойства кривых, инвариантные относительно
ортогонального проецирования
1.
Касательная к кривой проецируется в касательную к ее про-
екции.
l
100
2.
Несобственным точкам кривой соответствуют несобственные
точки ее проекции.
При проецировании плоских кривых, в дополнение к отме-
ченным, справедливы следующие свойства:
3.
Порядок проекции алгебраической кривой (в общем случае)
равен порядку самой кривой.
4.
Число узловых точек на проекции кривой, вообще говоря,
равно числу узловых точек самой кривой.
Из пространственных кривых в технике широкое примене-
ние находят винтовые линии.
1 2
1
≡
0
1
1 1
1
0
2
π
• d
1 2
0
1 1
0
1 0
0
9
0
8
0
7
0
6
0
5
0
4
0
3
0
2
0
1
0
1 2
1
1 1
1
1 0
1
9
1
8
1
7
1
6
1
5
1
4
1
3
1
2
1
1
1
0
1
≡
0
0
1
2
2
2
3
2
4
2
5
2
6
2
7
2
8
2
9
2
1 0
2
1 1
2
1 2
2
i
2
1 0
1
9
1
8
1
7
1
6
1
5
1
4
1
3
1
2
1
1
1
d
i
1
P
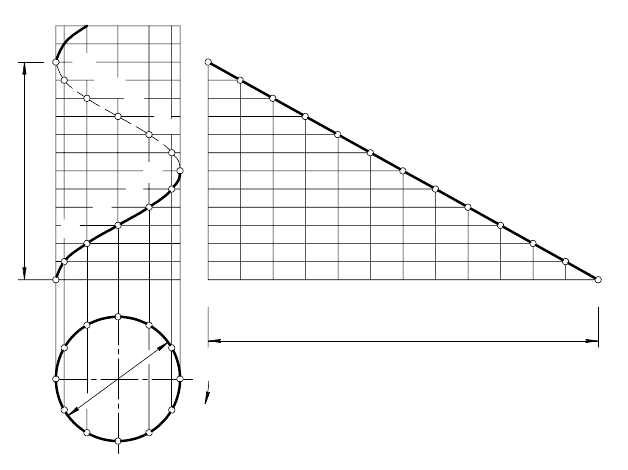
Рис. 109
Цилиндрическая винтовая линия (гелиса) — пространствен-
ная кривая, представляющая собой траекторию точки, выпол-
няющей винтовое движение. Винтовое движение включает в
себя одновременно равномерное поступательное движение точ-
ки по прямой и равномерное вращательное движение этой пря-
мой с точкой вокруг оси i, которой прямая параллельна
(рис. 109). Если ось i винтовой линии перпендикулярна
гори-

101
зонтальной плоскости проекций, то горизонтальная проекция
винтовой линии есть окружность, фронтальная — синусоида.
Величина Р перемещения точки в направлении оси, соответст-
вующая одному ее обороту вокруг оси, называется шагом винто-
вой линии.
Для построения проекций цилиндрической винтовой линии
(гелисы), предварительно строят проекции прямого кругового
цилиндра (рис. 109). Окружность основания цилиндра (горизон-
тальную проекцию гелисы) делят на равные части. На такое же
число равных частей делят шаг (на фронтальной проекции). Из
точек деления окружности проводят вертикальные линии связи,
а через точки деления шага — горизонтальные
прямые. Отмеча-
ют точки 0
2
, 1
2
, 2
2
, … 12
2
, в которых пересекаются соответст-
венные прямые, и соединяют их между собой плавной кривой.
Полученная кривая линия (синусоида) — фронтальная про-
екция гелисы.
Гипотенуза треугольника 12
1
12
0
0
0
(рис. 109) является раз-
верткой гелисы на протяжении шага. Т. е. цилиндрическая вин-
товая линия на развертке обращается в прямую линию. Такая
кривая линия соединяет две точки цилиндрической поверхности
(например, 0 и 12 ) кратчайшим путем и называется геодезиче-
ской линией.
8.3. КОНИЧЕСКИЕ СЕЧЕНИЯ. ОРТОГОНАЛЬНЫЕ
ПРОЕКЦИИ ОКРУЖНОСТИ
Кривые второго порядка (окружность, эллипс, гипербола и
парабола) находят большое применение в практике техническо-
го проектирования. Эти кривые являются коническими сече-
ниями (см. 10.4.).
Ортогональные проекции окружности
Окружность — плоская кривая второго порядка является ча-
стным случаем эллипса. Она определяется центром О и радиу-
сом R: О
(О, R ). На чертеже обычно ставят размер диаметра ок-
ружности. Ортогональные проекции окружности меняются в
зависимости от расположения ее плоскости по отношению к
плоскости проекций.
Если плоскость окружности параллельна плоскости проек-
ций (α || π
1
, рис. 110, а), то на эту плоскость проекций окруж-
