Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.

62
ные проекции пересекаются в точке i
2
, являющейся фронталь-
ной проекцией линии их пересечения i : δ
2
≡ f
0
δ
I
α
2
≡ f
0
α
= i
2
⇒
⇒ δ I α = i.
p
2
p
1
d
2
≡
f
0
d
i
2
a
2
≡
f
0
a
i
1
i
a
d
i
1
i
2
d
2
≡
f
0
d
a
2
≡
f
0
a
а б
Рис. 67
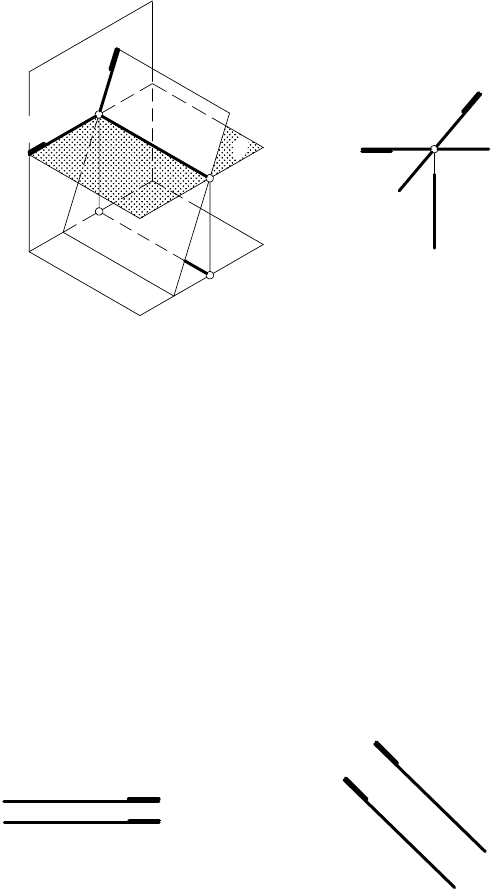
При определении на эпюре взаимного расположения плос-
костей, необходимо обращать внимание не только на располо-
жение проекций или следов, но и на их обозначение. Напри-
мер, на рис. 68 заданы плоскости α (α
1
≡ h
0
α
) и β ( β
2
≡ f
0
β
). Их
проекции параллельны α
1
|| β
2
, а плоскости пересекаются:
α I β = l. Это объясняется тем, что α
1
— горизонтальная проек-
ция плоскости α, а β
2
— фронтальная проекция β, т. е. проек-
ции не одноименные.
Фронтально проецирующая плоскость γ и горизонтально
проецирующая плоскость δ на рис. 69 имеют параллельные про-
екции (γ
2
|| δ
1
), но в пространстве пересекаются по прямой
а (а
1
, а
2
), проекции которой совпадают с одноименными проек-
циями этих плоскостей:
γ I δ = а (а
1
, а
2
) ∧ а
1
≡ δ
1
, а
2
≡ γ
2
.
b
2
≡
f
0
b
≡
l
2
a
1
≡
h
0
a
≡
l
1
g
2
≡
a
2
d
1
≡
a
1
Рис. 68 Рис. 69
63
4.3. ПЛОСКОСТЬ ЧАСТНОГО ПОЛОЖЕНИЯ И ПЛОСКОСТЬ
ОБЩЕГО ПОЛОЖЕНИЯ
Очевидно, что плоскость частного положения и плоскость
общего положения всегда пересекаются. Линия пересечения
принадлежит обеим плоскостям. Поэтому одна проекция линии
пересечения определяется без дополнительных построений: она
совпадает с вырожденной одноименной проекцией (или одно-
именным следом) плоскости частного положения. Вторую про-
екцию линии пересечения определяют как проекцию прямой,
принадлежащей плоскости общего положения
.
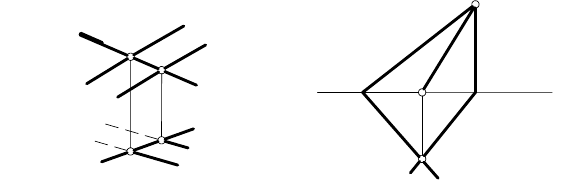
На рис. 70 построена линия пересечения l плоскости общего
положения α (а || b) с фронтально проецирующей плоскостью β.
Ее фронтальная проекция l
2
совпадает с фронтальной проекци-
ей плоскости β
2
, а горизонтальная проекция определена с по-
мощью точек 1 и 2, принадлежащих плоскости α: 1 ∈ а ⊂ α,
2 ∈ b ⊂ α.
Если плоскости заданы следами (рис. 71), то одна проекция
линии пересечения совпадает со следом плоскости частного по-
ложения (а
1
≡ h
0
δ
), а фронтальная проекция этой линии строит-
ся с помощью ее следов H
a
и F
a
: а
2
(
22
aa
FH
).
b
1
a
2
b
2
a
1
l
2
≡
b
2
≡
f
0
b
2
2
1
2
l
1
1
1
2
1
F
a
≡
F
a
2
a
2
H
a
2
x
g
x
f
0
d
H
a
≡
H
a
1
d
1
≡
h
0
d
≡
à
1
x
d
≡
F
a
1
h
0
g
f
0
g
Рис. 70 Рис. 71
4.4. ПРЯМАЯ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ.
АЛГОРИТМ ПОСТРОЕНИЯ ТОЧКИ ПЕРЕСЕЧЕНИЯ
ПРЯМОЙ С ПЛОСКОСТЬЮ
Точку пересечения прямой и плоскости общего положения
определяют с помощью дополнительных построений, основан-
64
ных на построении линии пересечения плоскости частного по-
ложения с плоскостью общего положения (см. 4.3.).
При любом задании прямой и плоскости общего положения
дополнительные построения для определения точки пересече-
ния одинаковы и выполняются в определенном порядке, отра-
женном в алгоритме (рис. 72, а и б ).
Алгоритм построения точки пересечения прямой с плоскостью
1. Заключить прямую в плоскость частного положения:
l ⊂ α
2. Построить линию пересечения заданной плоскости с плоско-
стью частного положения:
γ I
α
= (12 )
3. Определить точку пересечения заданной прямой с линией пере-
сечения плоскостей:
K = l I (12 )
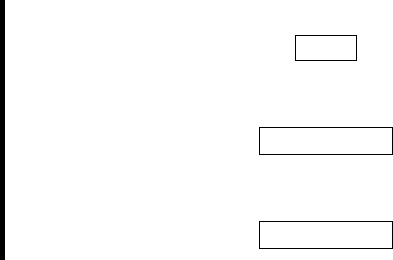
На рис. 72, а дано аксонометрическое изображение и гори-
зонтальная проекция плоскости γ (UABC), и прямой l, пересе-
кающихся в точке K, а также горизонтально проецирующей
плоскости α (α
1
≡ h
0
α
), в которую заключена прямая l.
На эпюре построения выполнены в соответствии с алгорит-
мом (рис. 72, б ). Ниже приводится символическая запись этих
построений:
1. l ⊂ α ⊥ π
1
⇔ α
1
≡ l
1
;
2. γ (UABC ) I α = (12 ) ⇒
⎪
⎩
⎪
⎨
⎧
⎩
⎨
⎧
γ⊂⊂
γ⊂⊂
αγ=
);(
);(
)(
;)(
2222222
2222222
22
1111111
CBACA2
CBABA1
21
)CB(A21 I
3. l I (12 ) = K ⇒
⎪
⎩
⎪
⎨
⎧
⊂
=
.lK
K21l
11
2222
;)(I
Видимость прямой l относительно плоскости γ (
U
ABC ) оп-
ределена на рис. 72, б с помощью конкурирующих точек 1 и 3,
4 и 5 (см. 2.3.), одна из которых принадлежит прямой, а другая
— плоскости.
65
Границами видимости проекций прямой являются проекции
точки пересечения прямой с плоскостью K
1
и K
2
.
Видимость горизонтальной проекции прямой l определена с
помощью горизонтально конкурирующих точек 1 и 3.
Точка 1 принадлежит плоскости γ (
U
ABC ), а точка 3 лежит
на прямой l. Видна горизонтальная проекция 1
1
, так как точка 1
расположена выше точки 3 (направление взгляда на чертеже
обозначено стрелкой). Точка 1 лежит на плоскости, поэтому
прямая l
1
не видна слева от точки K
1
(прямая расположена под
плоскостью).
A
1
C
1
C
2
1
1
1
Â
1
Â
À
1
2
l
K
2
K
1
h
0
a
≡
a
1
≡
l
1
p
1
a
A
1
Â
1
C
1
A
2
Â
2
C
2
1
1
≡
( 3
1
)
( 4
2
)
≡
5
2
2
1
4
1
5
1
2
2
3
2
1
2
K
1
K
2
l
2
a
1
≡
l
1
а б
Рис. 72
Аналогично определяется видимость фронтальной проекции
прямой с помощью фронтально конкурирующих точек 4 и 5.
Точка 4 принадлежит плоскости (4 ⊂ [BC
] ⊂ γ ), а точка 5 лежит
на прямой l. Видна проекция 5
2
, так как точка 5 ближе к на-
блюдателю, чем точка 4. Значит проекция l
2
видна справа от
точки K
2
(прямая l на этом участке расположена перед
плоскостью).
4.5. ДВЕ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ.
АЛГОРИТМ ПОСТРОЕНИЯ ТОЧКИ, ПРИНАДЛЕЖАЩЕЙ
ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Две плоскости пересекаются по прямой линии, для опреде-
ления которой достаточно найти две точки, принадлежащие од-
новременно каждой из заданных плоскостей.
66
Общую точку заданных плоскостей строят в определенном
порядке: вводят третью вспомогательную плоскость частного
положения, находят линии пресечения вспомогательной плос-
кости с каждой из плоскостей (см. 4.3.), отмечают точку пересе-
чения построенных линий.
Повторив предложенные операции, получают вторую точку
линии пересечения плоскостей.
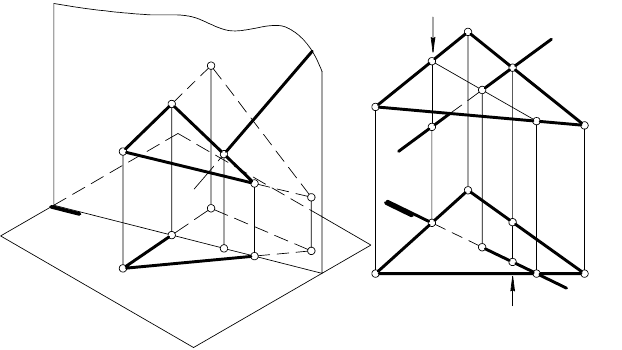
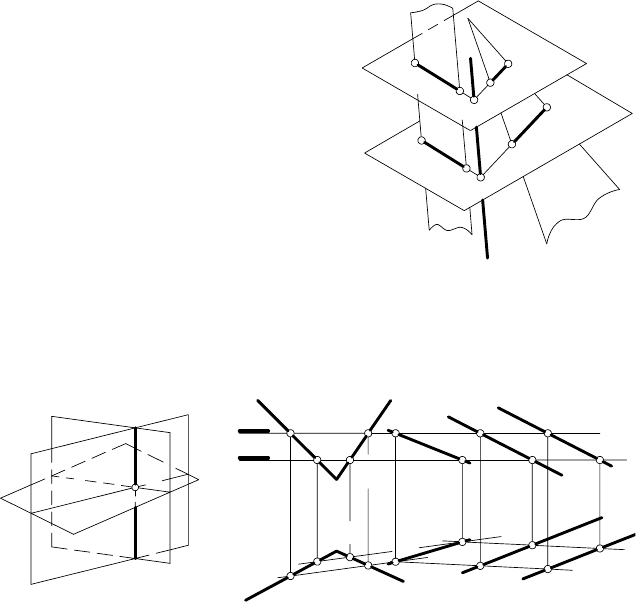
На рис. 73 дано аксонометрическое изображение и символи-
ческое описание построения
линии пересечения плоскостей
γ (a || b) и δ (с I d ):
1. α
1
|| π
1
;
2. α
1
I γ = (12 );
3. α
1
I δ = (34 );
4. (12 )
I (34 ) = K
1
;
5. α
2
|| π
1
;
6. α
2
I γ = (56 );
7. α
2
I δ = (78 );
8. (56 )
I (78 ) = K
2
;
9. K
1
U K
2
= K
1
K
2
.
Каждая из двух точек, принад-
лежащих линии пересечения
плоскостей, строится в одном и
том же порядке, отраженном в
алгоритме (рис. 74).
a
b
g
j
n
j
m
j
K
j
1
1
5
1
6
1
2
1
b
1
a
1
m
1
n
1
K
2
1
K
1
1
K
2
2
K
1
2
7
1
8
1
4
1
3
1
4
2
8
2
7
2
3
2
5
2
1
2
2
2
6
2
m
2
n
2
b
2
a
2
g
1
2
g
2
2
Рис. 74 Рис. 75
Рис. 73
g
d
a
1
a
2
K
1
1
2
3
4
5
6
7
8
a
b
c
d
K
2
67
Алгоритм построения точки, принадлежащей линии пересечения
двух плоскостей
1. Ввести вспомогательную секущую плоскость частного поло-
жения:
γ
j-
2. Определить линии пересечения вспомогательной плоскости ча-
стного положения с каждой из заданных плоскостей:
m
j
=
γ
j
I α n
j
=
γ
j
I β-
3. Найти точку пересечения полученных линий:
K
j
= m
j
I n
j-
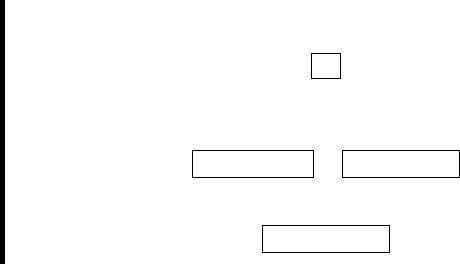
ЗАДАЧА. Построить проекции линии пересечения плос-
костей α (a I b) и β (m || n) (рис. 75).
РЕШЕНИЕ.
1.
Вводится вспомогательная плоскость γ
1
|| π
1
.
2.
Определяются линии пересечения: (12 ) — плоскости γ
1
с
плоскостью α (a I b) и (34 ) — плоскости γ
1
с
плоскостью β (m || n).
3.
Находится точка пересечения линий:
K
1
= (12 )
I (34 ).
Горизонтальная проекция K
1
1
определяется как точка пере-
сечения 1
1
2
1
с 3
1
4
1
, а фронтальная проекция
1
2
K
— по верти-
кальной линии связи на
1
2
γ
, так как точка K принадлежит
вспомогательной плоскости γ
1
.
4.
Вводится вспомогательная плоскость γ
2
|| π
1
.
5.
Строятся линии пересечения:
(56 ) = γ
2
I α ;
(78 ) = γ
2
I β ;
6.
Определяется точка пересечения построенных линий:
K
2
= (56 )
I (78 ) ⇒
⎪
⎩
⎪
⎨
⎧
γ∈
=
.K
8765K
2
2
2
2
1111
2
1
);()( I
7.
Одноименные проекции точек соединяют между собой и
получают проекции линии пересечения плоскостей:
K
1
U K
2
= (K
1
K
2
)
(
2
2
1
2
2
1
1
1
, KKKK
).
68
Линию пересечения плоскостей с помощью двух принадле-
жащих ей точек можно построить также, определяя каждую из
них, как точку пересечения прямой одной плоскости с другой
плоскостью (см. 4.4.).
4.6. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ И ПЛОСКОСТИ.
ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
Согласно признаку перпендикулярности прямой и плоско-
сти: прямая перпендикулярна плоскости, если она перпендикулярна
двум пересекающимся прямым этой плоскости.
Для построения проекций перпендикуляра к плоскости на
эпюре, в плоскости проводят две ее главные линии: горизонталь
и фронталь.
Теорема. Если прямая перпендикулярна к плоскости, то горизон-
тальная проекция этой прямой перпендикулярна горизонтальной
проекции горизонтали, а фронтальная проекция прямой — фрон-
тальной проекции фронтали той же плоскости.
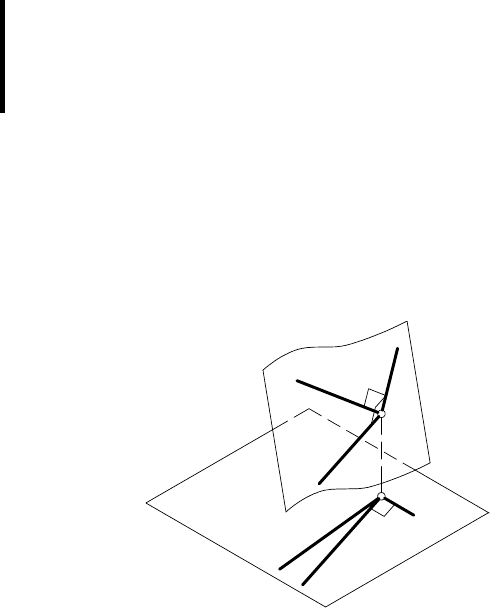
На рис. 76 показана прямая l, перпендикулярная плоско-
сти α. Пусть прямая l пересекает плоскость α в точке А. Если в
плоскости α провести через точку A горизонталь h, то на осно-
вании теоремы об ортогональных проекциях прямого угла
(см. 3.2.) h
1
⊥
l
1
. Аналогичны рассуждения и для фронтали f,
проведенной в плоскости α через точку A. Прямой угол между
фронталью f и прямой l проецируется прямым на плоскость π
2
,
поэтому l
2
⊥ f
2
.
a
A
1
p
1
f
1
h
1
l
1
A
h
f
l
Рис. 76

69
Справедлива и обратная теорема:
если проекции прямой перпендикулярны одноименным проекциям
горизонтали и фронтали плоскости, то такая прямая перпенди-
кулярна этой плоскости.
Действительно, если горизонтальная проекция горизонтали
плоскости перпендикулярна горизонтальной проекции прямой,
то горизонталь перпендикулярна самой прямой (см. теорему об
ортогональной проекции прямого угла 3.2.). На основании той
же теоремы можно утверждать, что и фронталь плоскости пер-
пендикулярна этой прямой. Значит прямая перпендикулярна
двум пересекающимся прямым (h I f ), расположенным в плос-
кости, и
поэтому перпендикулярна к данной плоскости.
Взаимно перпендикулярные плоскости
Из стереометрии известно, что
две плоскости взаимно перпендикулярны, если одна из них прохо-
дит через перпендикуляр к другой.
Это положение позволяет строить взаимно перпендикуляр-
ные плоскости на эпюре с помощью проведения перпендикуля-
ра к одной из них.
a
b
d
g
n
Рис. 78
Через перпендикуляр к плоскости проходит бесконечное
множество плоскостей, перпендикулярных данной плоскости
(рис. 78). Искомую плоскость выбирают из этого множества,
определяя ее положение общим для всех плоскостей перпенди-
куляром n и еще каким-нибудь элементом, принадлежащим
этой плоскости (см. 3.3.).

70
ЗАДАЧА. Построить плоскость α, перпендикулярную
плоскости
U
ABC и проходящую через прямую l (рис. 79).
A
1
A
2
B
2
B
1
C
2
C
1
1
1
2
1
f
1
h
1
f
2
2
2
1
2
D
2
D
1
m
1
l
1
l
2
m
2
Рис. 79
РЕШЕНИЕ.
1.
В плоскости
U
ABC проводят h и f.
Горизонталь проведена через точку A и пересекает (BC ) в
точке 1.
Фронталь определена точками С и 2.
2.
На прямой l выбирают произвольную точку D:
D
2
∈ l
2
D
1
∈ l
1
⎭
⎬
⎫
⇒ D ∈ l.
3.
Через точку D проводят перпендикуляр m к плоскости
U
ABC:
D
1
∈ m
1
⊥ h
1
D
2
∈ m
2
⊥ f
2
⎭
⎬
⎫
⇒ D ∈ m ⊥
U
ABC.
4.
Плоскость α, перпендикулярная к плоскости
U
ABC, прохо-
дящая через l, определена на эпюре двумя пересекающимися
прямыми m и l
: α (m I l ) ⊥
U
ABC.

71
Лекция 5 (2 часа)
Тема «Многогранники»
План
1.
Многогранники и их расположение на эпюре.
2.
Сечение многогранника плоскостью.
3.
Алгоритм построения точек пересечения многогранника с
прямой линией.
4.
Взаимное пересечение многогранников.
5.1. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ МНОГОГРАННИКОВ
Многогранником называют пространственную фигуру, ограни-
ченную замкнутой поверхностью, состоящей из плоских много-
угольников, каждая сторона которых принадлежит одновременно
двум из них.
Многоугольники называют гранями, их стороны — ребрами,
а вершины — вершинами многогранника. Совокупность всех
граней многогранника образует его поверхность.
Далее будут рассматриваться только выпуклые многогранни-
ки.
Многогранник, все грани которого располагаются по одну сторо-
ну от плоскости каждой из них, называются выпуклыми.
Пирамида — многогранник, в основании которого лежит произ-
вольный многоугольник, а боковые грани — треугольники с общей
вершиной.
На рис. 80, а дано наглядное изображение пирамиды
SABCDE, а на рис. 80, б — ее ортогональные проекции.
На эпюре многогранники задают проекциями их ребер и
вершин. Видимость ребер определяют с помощью конкурирую-
щих точек (рис. 80, б
). Крайние ребра многогранников всегда
видимы.
Призма — многогранник, у которого основания — два равных и
взаимно параллельных многоугольника, а боковые грани — парал-
лелограммы.
