Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.

52
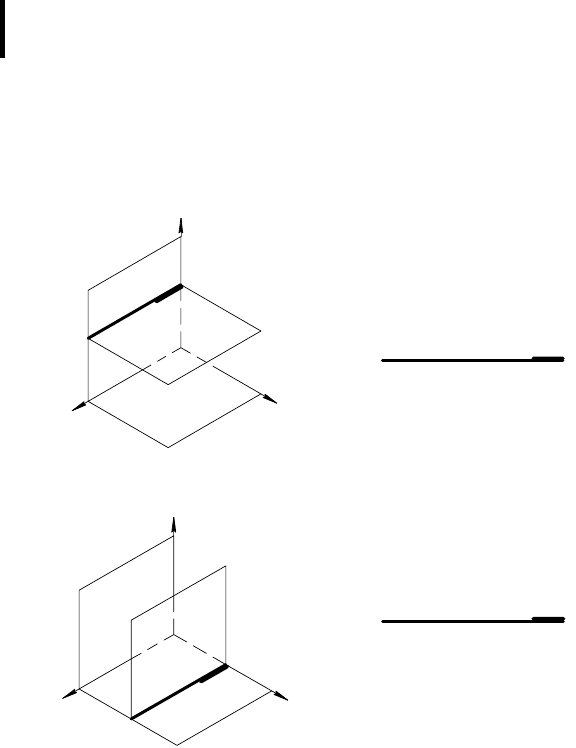
Профильно проецирующую плоскость можно задать на эпю-
ре одной ее вырожденной в прямую проекцией, совпавшей с ее
профильным следом (рис. 52, в).
Плоскости уровня
Плоскость, параллельная одной из плоскостей проекций, называ-
ется плоскостью уровня.
Плоскости уровня различают в зависимости от того, какой
плоскости проекций каждая из них параллельна: π
1
, π
2
или π
3
.
1. Горизонтальная плоскость δ ||
π
1
(рис. 53, а и б ). Горизон-
тальную плоскость задают на эпюре одной, вырожденной в
прямую, фронтальной проекцией, совпавшей с ее фронтальным
следом δ
2
≡ f
0
δ
.
x
y
z
p
1
Î
p
2
d
d
2
≡
f
0
d
d
2
≡
f
0
d
а б
Рис. 53
x
y
z
p
1
Î
p
2
e
1
≡
h
0
e
e
e
1
≡
h
0
e
а б
Рис. 54

53
x
y
z
p
1
Î
p
2
p
3
x
x
2
≡
f
0
x
x
2
≡
f
0
x
x
1
≡
h
0
x
а б
Рис. 55
2. Фронтальная плоскость ε
||
π
2
(рис. 54, а и б
). Фронталь-
ную плоскость задают на эпюре вырожденной в прямую гори-
зонтальной проекцией, совпавшей с ее горизонтальным следом
ε
1
≡ h
0
ε
.
3. Профильная плоскость уровня ξ || π
3
(рис. 55, а и б
).
Профильную плоскость задают на эпюре одной из ее вырож-
денных в прямую проекций: фронтальной — совпавшей с ее
фронтальным следом ξ
2
≡ f
0
ξ
(рис. 55, б
) или горизонтальной —
совпавшей с ее горизонтальным следом ξ
1
≡ h
0
ξ
(рис. 55, а).
3.6. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
Главные линии плоскости — это линии уровня, принадле-
жащие плоскости, и линии наибольшего наклона этой плоско-
сти к плоскостям проекций:
1. Горизонталь — прямая, принадлежащая плоскости и парал-
лельная горизонтальной плоскости проекций.
2. Фронталь — прямая, принадлежащая плоскости и параллельная
фронтальной плоскости проекций.
3. Линия наибольшего наклона плоскости к горизонтальной плос-
кости проекций (линия ската) — прямая, принадлежащая
плоскости и перпендикулярная к горизонтали этой плоскости.
4. Линия наибольшего наклона плоскости к фронтальной плоско-
сти проекций — прямая, принадлежащая плоскости и перпен-
дикулярная к фронтали этой плоскости.
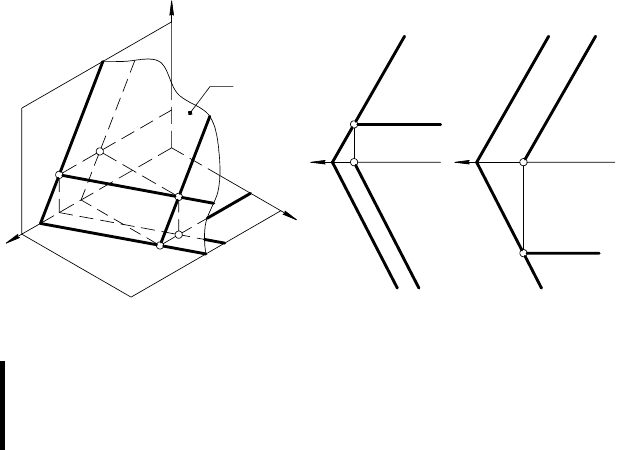
54
На рис. 56, а изображены горизонталь h и фронталь f, при-
надлежащие плоскости α, заданной следами. Горизонтальный
след плоскости α — h
0
α
= α I π
1
, а ее фронтальный след —
f
0
α
=α I π
2
.
Любая горизонталь плоскости (по определению) параллель-
на π
1
и принадлежит этой плоскости, следовательно, все гори-
зонтали одной плоскости параллельны ее горизонтальному сле-
ду h
0
α
.
Рассуждая аналогично о фронталях плоскости, приходим к
выводу: все фронтали одной плоскости параллельны ее фронталь-
ному следу и параллельны между собой.
На рис. 56, б даны проекции горизонтали h (h
1
, h
2
), принад-
лежащей плоскости α (
f
0
α
I h
0
α
):
⎪
⎩
⎪
⎨
⎧
≡
≡
⇔
α
αα
α
.||
;||
||
2
1
02
001
0
xhh
hhh
hh
Î
p
2
x
y
z
p
1
h
h
1
h
2
f
2
f
1
f
h
0
a
f
0
a
x
f
0
a
h
1
f
2
x
h
0
a
f
1
h
2
f
0
a
1
≡
h
0
a
2
h
0
a
≡
h
0
a
1
f
0
a
≡
f
0
a
2
X
a
X
a
X
a
F
h
≡
F
h
2
H
f
≡
H
f
1
a
f
0
a
1
≡
h
0
a
2
F
h
H
f
H
f
2
F
h
1
а б в
Рис. 56
Горизонтальная проекция горизонтали плоскости параллельна
горизонтальному следу этой плоскости, а фронтальная проекция
горизонтали параллельна оси х.
Проекции фронтали, расположенной в плоскости
α (f
0
α
I h
0
α
), показаны на рис. 56, в:
⎪
⎩
⎪
⎨
⎧
≡
≡
⇔
αα
α
α
.||
;||
||
002
01
0
2
1
fff
xff
ff
55
Горизонтальная проекция фронтали плоскости параллельна оси х,
а фронтальная проекция фронтали плоскости параллельна фрон-
тальному следу этой плоскости.
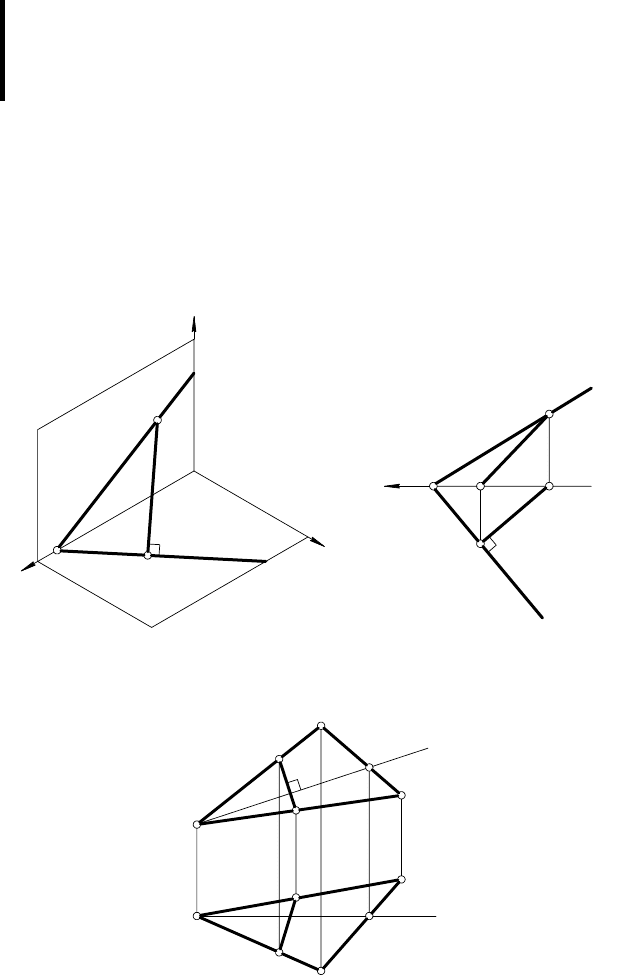
Линия наибольшего наклона n плоскости α к плоскости π
1
(линия ската) построена на рис. 57, а. Прямая n принадлежит
плоскости α (h
0
α
I f
0
α
), так как две ее точки F
n
и H
n
принадлежат
этой плоскости, и перпендикулярна горизонтальному следу
плоскости h
0
α
. На эпюре (рис. 57, б
) угол между горизонталь-
ным следом и линией n спроецировался прямым на π
1
(см. 3.2.):
1
001 αα
≡⊥ hhn
.
Î
p
2
x
y
z
p
1
x
X
a
f
O
a
h
0
a
n
X
a
H
n
2
F
n
1
F
n
≡
F
n
2
n
1
n
2
h
0
a
≡
h
0
a
1
f
0
a
≡
f
0
a
2
H
n
≡
H
n
1
F
n
≡
F
n
2
H
n
≡
H
n
1
а б
Рис. 57
A
1
C
1
B
1
B
2
A
2
C
2
D
1
1
1
E
1
E
2
f
1
1
2
D
2
f
2
Рис. 58

56
Линия наибольшего наклона [DE ] плоскости β (UАВС
) к
плоскости проекций π
2
построена на рис. 58. Порядок построе-
ния:
f ⊂ β (UАВС )
β ⊃ [DE ] ⊥ f .
Итак, линию наибольшего наклона плоскости к плоскости проек-
ций π
1
(или π
2
) определяют следующие построения:
1. Провести произвольную горизонталь (или фронталь), принадле-
жащую данной плоскости.
2. Провести произвольный перпендикуляр к горизонтали (или
фронтали), расположенный в этой плоскости.
3.7. УГОЛ НАКЛОНА ПЛОСКОСТИ К ПЛОСКОСТИ ПРОЕКЦИЙ
Углом наклона плоскости к плоскости проекций называют
двугранный угол, образованный этой плоскостью и плоскостью
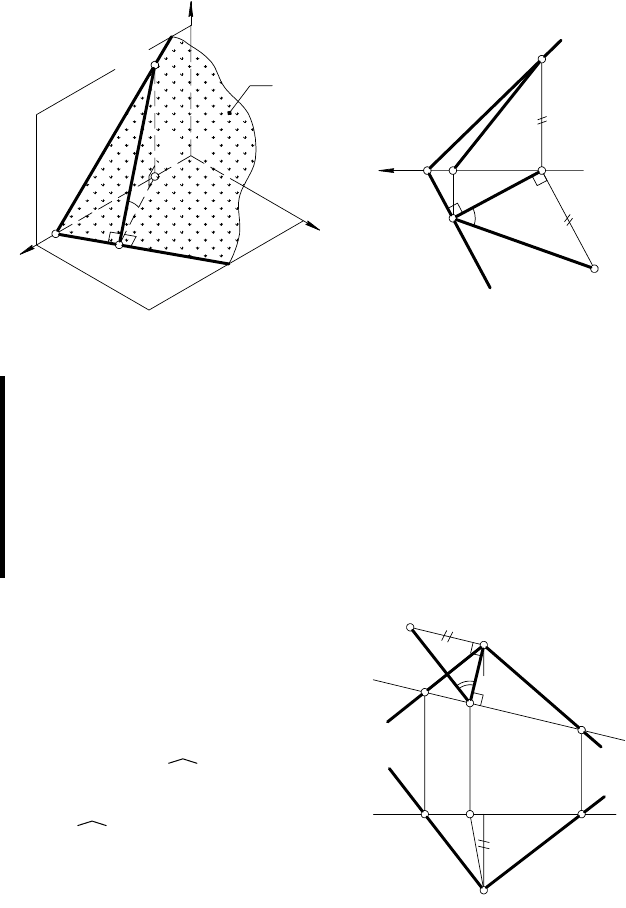
проекций. На рис. 59, а угол наклона плоскости β к плоско-
сти π
1
— двугранный угол, образованный плоскостями β и π
1
.
Горизонтальный след плоскости β —
ребро этого двугранного
угла, а полуплоскости β и π
1
, находящиеся по одну сторону от
ребра h
0
β
— его грани. Двугранный угол измеряется его линей-
ным углом.
Как известно, линейным углом двугранного угла называют
угол, образованный двумя перпендикулярами к ребру, проведенными
из одной его точки и расположенными в гранях.
Линейный угол ВАВ
1
образуют отрезок [АВ], линии наи-
большего наклона плоскости β к плоскости проекций π
1
, и его
ортогональная проекция на плоскость π
1
— А
1
В
1
.
Угол α° = ВАВ
1
на эпюре (рис. 59, б
) строят с помощью
прямоугольного треугольника (см. 2.7.), определяя угол наклона
отрезка [АВ] ⊥
h
0
β
к плоскости проекций π
1
.
57
Î
p
2
x
y
z
p
1
x
B
0
X
b
A
≡
A
1
b
f
0
b
h
0
b
B
1
A
≡
A
1
B
≡
B
2
A
2
X
b
a Å
B
1
a Å
f
0
b
h
0
b
B
≡
B
2
а б
Рис. 59
Угол наклона плоскости общего положения к плоскости проек-
ций π
1
(или π
2
) определяют с помощью следующих построений:
1. В данной плоскости общего положения проводят ее линию наи-
большего наклона к плоскости π
1
(или π
2
) и берут на ней произ-
вольный отрезок.
2. С помощью прямоугольного треугольника определяют угол на-
клона выбранного отрезка к плоскости проекций π
1
(или π
2
).
На рис. 60 определен угол на-
клона β° плоскости α (а I b) к
плоскости проекций π
2
. Порядок
построения:
1. а) f (12
) ⊂ α (а I b);
б) α ⊃ [АВ
] ⊥ f.
2. а) UА
2
В
2
А
0
(А
0
А
2
В
2
= 90°),
| А
0
А
2
| = ∆y = | y
A
— y
B
|;
б) А
0
В
2
А
2
= β°.
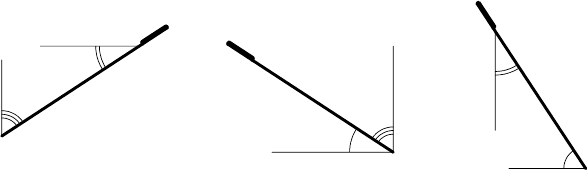
Углы наклона α°, β° и γ° про-
ецирующих плоскостей к плоско-
стям проекций определяют без
дополнительных построений
(рис. 61, а, б и в) посредством про-
A
1
B
2
A
2
1
1
b
2
f
1
1
2
a
2
f
2
B
1
A
0
b Å
2
1
2
2
b
1
a
1
Рис. 60
58
ведения вертикальной и горизонтальной линий в произвольно
выбранных точках, расположенных на вырожденных в прямую
проекциях.
g Å
d
1
b Å
b Å
a Å
x
3
a Å
g Å
e
2
а б в
Рис. 61
59
Лекция 4 (2 часа)
Тема «Позиционные и метрические задачи»
План
1. Прямая и плоскость частного положения.
2. Две плоскости частного положения.
3. Плоскость частного положения и плоскость общего положения.
4. Прямая и плоскость общего положения. Алгоритм построе-
ния точки пересечения прямой с плоскостью.
5. Две плоскости общего положения. Алгоритм построения
точки, принадлежащей линии пересечения двух плоскостей (по-
верхностей).
6. Перпендикулярность
прямых и плоскостей.
4.1. ПРЯМАЯ И ПЛОСКОСТЬ ЧАСТНОГО ПОЛОЖЕНИЯ
Плоскость частного положения задают на эпюре одной (вы-
рожденной в прямую линию) проекцией, совпадающей с ее од-
ноименным следом (см. 3.5.).
Для определения взаимного расположения любой прямой и плос-
кости, занимающей частное положение относительно плоско-
стей проекций, достаточно сравнить положение одной пары их
одноименных проекций.
Возможны три случая:
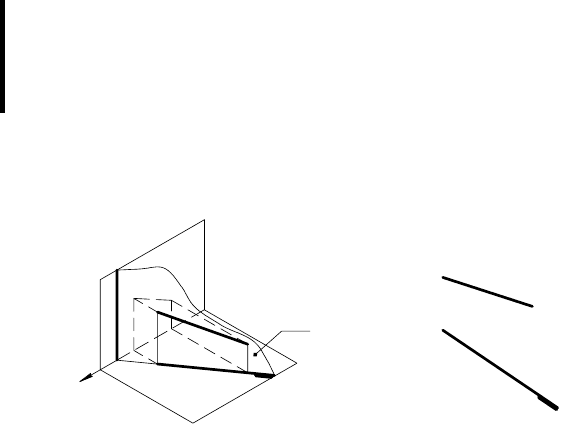
1. Одноименные проекции прямой и плоскости совпадают:
c
1
≡ α
1
, тогда в пространстве прямая принадлежит плоскости
(рис. 62, а и б );
x
p
1
Î
a
1
= h
0
a
= c
1
x
a
c
2
a
c
a
1
= h
0
a
= c
1
c
2
p
2
а б
Рис. 62
60
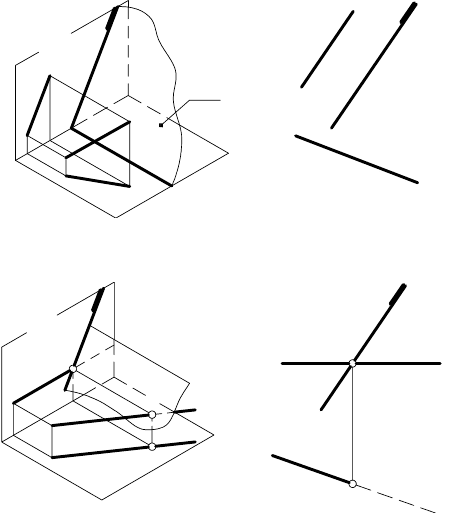
2. Одноименные проекции прямой и плоскости параллель-
ны:
α
2
|| β
2
— прямая а параллельна плоскости β (рис. 63, а и б );
3. Одноименные проекции прямой и плоскости пресекают-
ся: l
2
I γ
2
= K
2
(рис. 64, а и б ) — в пространстве прямая l пересе-
кает плоскость γ в точке K.
a
b
b
2
≡
f
0
b
a
2
a
a
1
p
1
p
2
a
1
a
2
b
2
≡
f
0
b
а б
Рис. 63
g
g
2
≡
f
0
g
p
1
p
2
K
1
K
K
2
l
2
l
1
l
l
1
K
1
K
2
l
2
g
2
≡
f
0
g
а б
Рис. 64
4.2. ДВЕ ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Две плоскости в пространстве могут занимать относительно
друг друга три положения (см. 1.3., табл. 5):
1. Быть параллельными;
2. Совпадать (частный случай параллельности, если расстоя-
ние между плоскостями равно 0);
3. Пересекаться.
61
Взаимное расположение двух плоскостей, занимающих частное
положение относительно плоскостей проекций, определяют на
эпюре по расположению их одноименных проекций:
1. Если одноименные проекции плоскостей параллельны, то и
плоскости параллельны;
2. Если одноименные проекции плоскостей совпадают, то и плос-
кости совпадают;
3. Если одноименные проекции плоскостей пересекаются, то и
плоскости пересекаются.
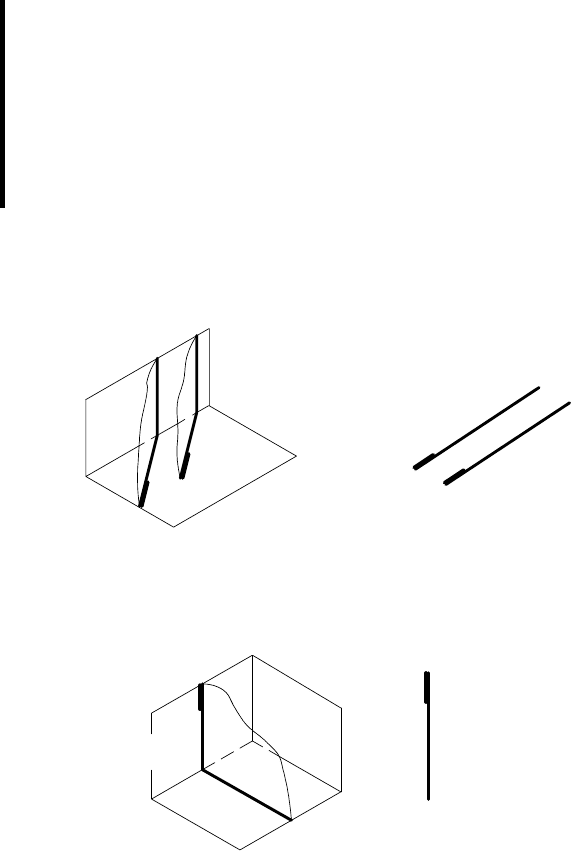
На рис. 65, а дано наглядное изображение параллельных
между собой горизонтально проецирующих плоскостей: α || β, а
на рис. 65, б плоскости α и β изображены на эпюре. Горизон-
тальные проекции плоскостей, совпавшие с их горизонтальны-
ми следами — параллельны: α
1
≡ h
0
α
|| β
1
≡ h
0
β
.
p
1
p
2
a
b
b
1
≡
h
0
b
a
1
≡
h
0
a
x
Î
b
1
≡
h
0
b
a
1
≡
h
0
a
а б
Рис. 65
На рис. 66, а дано аксонометрическое изображение про-
фильных плоскостей, совпадающих между собой: γ ≡ δ, а на
рис. 66, б эти плоскости изображены на эпюре: γ
2
≡ f
0
γ
≡ δ
2
≡ f
0
δ
.
p
1
p
2
x
p
3
g
≡
d
g
2
≡
f
0
g
≡
d
2
≡
f
0
d
g
2
≡
f
0
g
≡
d
2
≡
f
0
d
а б
Рис. 66
Аксонометрическое изображение пересекающихся горизон-
тальной плоскости δ и фронтально проецирующей плоскости α
дано на рис. 67, а: δ I α = i. На эпюре (рис. 67, б ) их фронталь-
