Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.

22
параллельную проекцию трех равных и взаимно перпендикулярных
отрезков
Ο
х, Оy, Оz, выходящих из некоторой точки простран-
ства.
На основании теоремы Польке системы аксонометрических
осей (см. рис. 11), а также отношение коэффициентов искаже-
ния по ним, могут быть заданы совершенно произвольно.
Между коэффициентами искажения и углом ϕ, образован-
ным направлением проецирования с плоскостью π
0
, существует
следующая зависимость:
ϕ+=++
2222
ctg2
000
zyx
KKK
. (1)
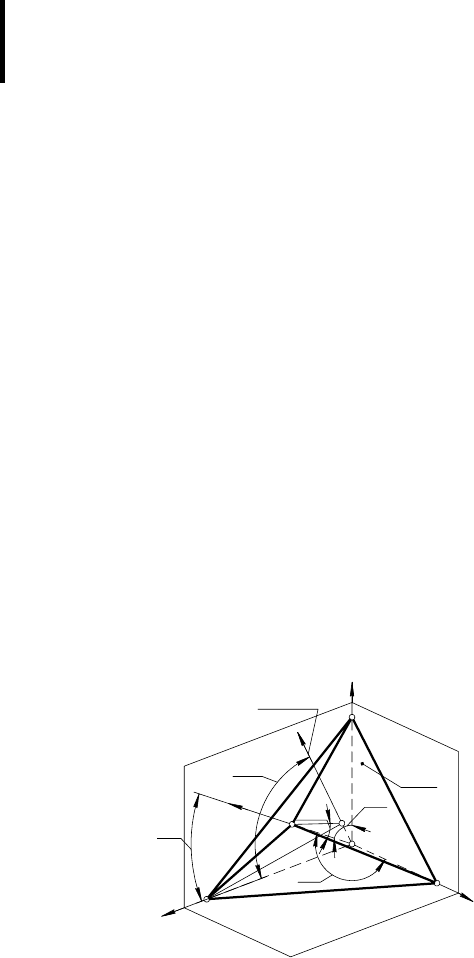
Для доказательства этого равенства обратимся к рис. 13, на
котором изображена прямоугольная система координат xyz и
плоскость аксонометрических проекций π
0
. Плоскость π
0
пере-
секает координатные оси в точках A, B и С, а плоскости проек-
ций — по прямым AВ, AС и ВС являющимися следами этой
плоскости. В связи с этим UABC называют треугольником сле-
дов. Направление проецирования задано отрезком ОО
0
, причем
точка О
0
является проекцией начала координат О на плос-
кость π
0
.
Отрезки О
0
A, О
0
В и О
0
С представляют собой аксонометри-
ческие оси координат. Угол ϕ, который образует направление
проецирования с плоскостью проекций π
0
, измеряется углом
ОО
0
D. Сторона О
0
D этого угла служит ортогональной проекци-
ей направления проецирования ОО
0
на плоскость π
0
. Точка D
является основанием перпендикуляра, опущенного из начала
координат О на плоскость проекций π
0
.
y
x
A
B
C
O
O
0
a
D
s
f Å
g
b
a
1
z
p
0
y
0
z
0
x
0
n
Ö
p
0
Рис. 13
23
Обозначим углы, образованные направлением проецирова-
ния ОО
0
с осями координат в пространстве, соответственно бу-
квами α, β, γ, а углы, образованные перпендикуляром ОD с те-
ми же осями, через α
1
, β
1
, γ
1
(на рис. 13 углы β
1
и γ
1
не обозна-
чены).
Для прямоугольной аксонометрии, когда ϕ° = 90°, сумма
квадратов коэффициентов искажения равна 2.
Стандартные аксонометрические проекции
Согласно стандарту из прямоугольных аксонометрических
проекций рекомендуется применять прямоугольные изометрию
и диметрию. Известно, что в прямоугольной аксонометрии
сумма квадратов коэффициентов искажения равна 2. Но в изо-
метрии
222
000
zyx
KKK ==
и, следовательно, 3
2
0
x
K
= 2, откуда
0
x
K = .,820
3
2
≈
Таким образом, в прямоугольной изометрии размеры пред-
мета по всем трем измерениям в направлениях осей x, y, и z со-
кращаются на 18%. Стандарт рекомендует изометрическую про-
екцию строить без сокращения по осям координат (брать при-
веденные коэффициенты искажения
000
zyx
KKK
=
=
=1), что
соответствует увеличению изображения относительно оригинала
в 1,22 раза.
При построении прямоугольной диметрической проекции
сокращение длин по оси y
0
принимают вдвое больше, чем по
двум другим, т. е. полагают, что
00
zx
KK = , а
00
50
xy
K,K
=
.
Тогда будем иметь:
2502
22
00
=+
xx
K,K
,
откуда
9
8
2
0
=
x
K и
940
0
,K
x
≈
, а 470
0
,K
y
≈ .
В практических построениях от таких дробных коэффициентов
обычно отказываются, вводя масштаб увеличения, определяе-
мый соотношением
061
940
1
,
,
= , и тогда приведенные коэффи-
циенты искажения по осям x
0
и z
0
равны единице, а по оси y
0
вдвое меньше: y = 0,5. Расположение осей прямоугольной изо-
метрии и диметрии показано соответственно на рис. 14 и 15.
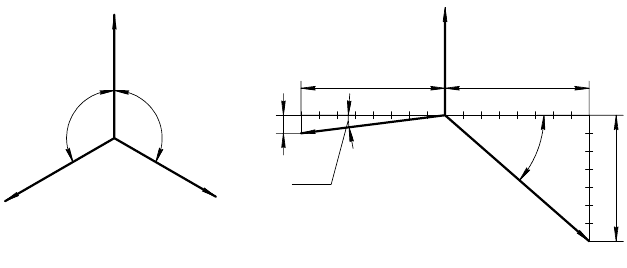
24
Î
0
x
0
y
0
z
0
1
8 8
7
=
4
1
Å
=
7
Å
Î
0
y
0
z
0
x
0
K
x
Î
:
K
y
Î
:
K
z
Î
= 1
:
1
:
1
1
2
0
Å
1
2
0
Å
K
x
Î
:
K
y
Î
:
K
z
Î
= 1
:
0 , 5
:
1
Рис. 14 Рис. 15
25
Лекция 2 (2 часа)
Тема «Проецирование точки и прямой»
План
1. Проецирование точки на две плоскости проекции.
2. Алгоритм построения 3-ей проекции точки.
3. Конкурирующие точки.
4. Проецирование прямой.
5. Принадлежность точки прямой линии.
6. Прямые частного положения.
7. Определение натуральной величины отрезка прямой ли-
нии и углов его наклона к плоскости проекций.
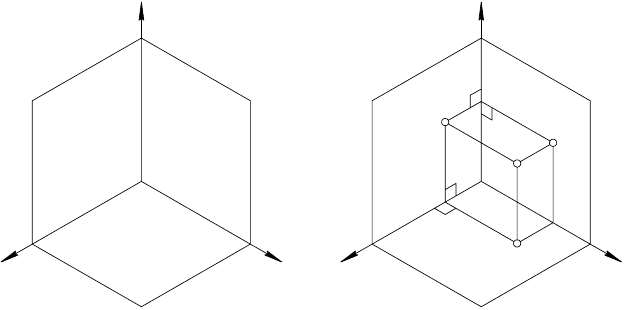
2.1. ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ ПЛОСКОСТИ
ПРОЕКЦИЙ
При проецировании оригинал располагают преимуществен-
но в первом октанте (рис. 16). Наблюдатель находится над
плоскостью π
1
, перед плоскостью π
2
и слева от плоскости π
3
.
Î
p
2
x
y
z
p
3
p
1
Î
x
y
z
A
A
1
A
3
A
2
x
ó
z
z
z
ó
ó
x
x
z
ó
p
2
p
3
p
1
A
z
A
x
A
y
Рис. 16 Рис. 17
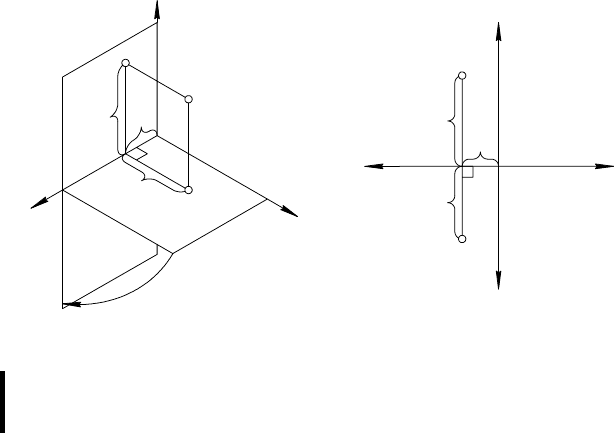
Возьмем в пространстве точку А и спроецируем ее ортого-
нально на плоскости π
1
, π
2
и π
3
(рис. 17).
26
Проводя через точку А проецирующие лучи, перпендикуляр-
ные π
1
, π
2
и π
3
, получим на этих плоскостях проекции точки А
(см. 1.5., свойство 1):
А
1
— горизонтальная проекция точки А;
А
2
— фронтальная проекция точки А;
А
3
— профильная проекция точки А.
Положение точки в пространстве определяется тремя коор-
динатами (x, y, z), показывающими величины расстояний, на
которые точка А удалена от плоскостей проекций. Отрезки:
[АА
3
] ≅ [ОА
x
] = х — абсцисса точки А;
[АА
2
] ≅ [ОА
y
] = у — ордината точки А;
[АА
1
] ≅ [ОА
z
] = z — аппликата точки А.
Конгруэнтность отрезков следует из равенства противопо-
ложных ребер в гранях прямоугольного параллелепипеда
АА
2
А
z
А
3
А
1
А
x
OА
y
(рис. 17).
Как уже отмечалось, положение точки в пространстве впол-
не определяется двумя ее проекциями (см. 1.4.3.). Обычно рас-
сматривают горизонтальную А
1
и фронтальную А
2
проекции
точки.
На рис. 18, а дано наглядное изображение точки А в прямо-
угольной изометрической проекции (см. 1.6.), а на рис. 18, б —
эпюр той же точки.
Î
x
y
z
A
A
1
A
2
ó
z
x
A
x
A
x
A
1
x
ó
z
A
2
y
Î
z
x
y
p
2
p
1
а б
Рис. 18
Эпюром точки называется чертеж, состоящий из двух (или бо-
лее) ее ортогональных проекций, связанных между собой.
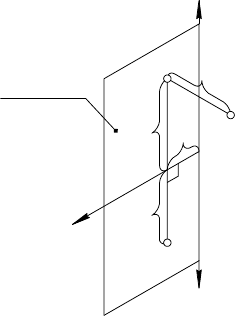
27
Проекции точки А
1
и А
2
на эпюре связаны общим перпенди-
куляром к оси x, проходящим через точку А
x
. Действительно,
если А
x
есть точка пересечения плоскости АА
1
А
x
А
2
с осью x
(риc. 18, а), а (А
1
А
x
) и (А
2
А
x
) — прямые, по которым эта плос-
кость пересекает плоскости проекций π
1
и π
2
, то А
1
А
x
⊥
А
2
А
x
⊥
x.
Это следует из того, что плоскость АА
1
А
x
А
2
перпендикулярна
плоскости π
1
(АА
1
⊥ π
1
) и π
2
(АА
2
⊥
π
2
), а значит перпендикулярна
линии их пересечения — оси x.
Прямые на эпюре, перпендикулярные координатным осям и
проходящие через две проекции одной точки, называют линиями
связи:
(А
1
А
2
) — вертикальная линия связи (рис. 18, б
),
(А
2
А
3
) — горизонтальная линия связи (рис. 21, а и б
).
При построении эпюра точки (рис. 18, б
) по ее наглядному
изображению (рис. 18, а) координаты точки А не искажаются,
так как в прямоугольной изометрической проекции приведен-
ные коэффициенты искажения по осям равны единице:
000
zyx
KKK == =1 (см. 1.6.).
Фронтальная проекция точки А остается на месте, т. е.
плоскость π
2
совмещается с плоскостью чертежа, а горизонталь-
ная вращается вместе с плоскостью π
1
вокруг оси x (как показа-
но на рис. 18, а) до совмещения с плоскостью π
2
. Положение
горизонтальной проекции А
1
на эпюре определяется координа-
тами x и y, а фронтальной проекции А
2
— координатами x и z;
т. е. если заданы две ортогональные проекции точки, то извест-
ны и координаты точки x, y, z, определяющие ее положение в
пространстве.
Эпюр точки на рис. 18, б — обра-
тимый чертеж (см. 1.4.). По этому
чертежу можно восстановить ориги-
нал, в данном случае точку А. Дей-
ствительно, пусть
π
2
совмещена с
плоскостью чертежа (рис. 19). Фрон-
тальная проекция А
2
не изменила
своего положения при переходе от
пространственной модели к эпюру.
Восстановив из точки А
2
перпенди-
куляр к плоскости чертежа
([А
2
А] ⊥
π
2
) и отложив на нем от точ-
ки А
2
отрезок [А
2
А] ≅ [А
x
А
1
] = у, полу-
чим в пространстве оригинал — про-
ецируемую точку А.
Рис.19
Î
x
y
z
A
A
2
ó
z
x
A
x
A
1
Ï ë î ñ ê î ñ ò ü
÷ å ð ò å æ à
p
2
p
1
y
28
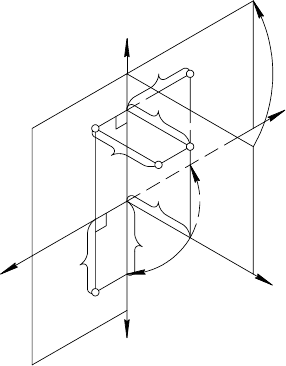
2.2. АЛГОРИТМ ПОСТРОЕНИЯ ТРЕТЬЕЙ
ПРОЕКЦИИ ТОЧКИ
При преобразовании про-
странственной модели в плоский
чертеж, профильная проекция А
3
будет вращаться вместе с про-
фильной плоскостью проекций
π
3
вокруг оси z и займет к концу
преобразования положение на
луче [А
2
А
z
) ⊥ z (рис. 20). Это за-
ключение следует из того, что
плоскость АА
2
А
z
А
3
проходит через
[АА
2
] ⊥
π
2
и [АА
3
] ⊥
π
3
, а значит,
перпендикулярна к оси z — ли-
нии пересечения этих плоско-
стей. Откуда: [А
2
А
z
] ⊥ z и
[A
3
A
z
] ⊥ z.
Расстояние от оси z до точ-
ки А
3
на эпюре равно ординате
точки А
([А
2
А]
≅ [А
z
А
3
] = y, см. 2.1.).
Исходя из сказанного выше, построение на эпюре профиль-
ной (горизонтальной) проекции точки по заданным горизон-
тальной (профильной) и фронтальной, можно выполнить, как
показано на рис. 21, а и б.
На рис. 21, а связь между горизонтальной проекцией А
1
и
профильной проекцией А
3
точки А установлена с помощью от-
резков [А
1
А
y
], [А
3
А
y
] и дуги окружности с центром в точке О,
радиусом [ОА
y
], а на рис. 21, б связь между проекциями уста-
новлена с помощью ломаной линии А
1
А
0
А
3
. Точка А
0
лежит на
биссектрисе угла, образованного осями у, расположенными в
плоскостях π
1
(O ⊂ у ⊥ х) и π
2
(O ⊂ у ⊥ z).
Биссектрису (ОА
0
) называют постоянной прямой чертежа
или постоянной прямой эпюра Монжа и обозначают k.
Положение профильной проекции точки А
3
определяется
координатами y и z точки A.
Рис. 20
Î
x
y
z
A
A
2
ó
A
x
A
1
p
2
p
1
y
A
3
A
y
A
y
A
y
ó
ó
ó
ó
ó
p
3
p
3
y
A
3
A
z
29
A
x
A
1
A
2
y
Î
z
x
y
A
3
A
y
z y
y
A
y
A
z
A
x
A
1
A
2
y
Î
z
x
y
A
3
A
y
z y
y
A
y
A
z
A
0
k
x x
а б
Рис. 21
Итак, положение точки в пространстве вполне определяется
заданием двух ее ортогональных проекций:
или А (А
1
, А
2
);
или А (А
2
, А
3
);
или А (А
1
, А
3
), так как сочетание любых двух ортогональных
проекций точки определяет значение трех ее координат x, y, z
(рис. 21, а и б
):
А
1
(x, y);
А
2
(x, z);
А
3
(y, z).
Следовательно, по двум любым
заданным ортогональным проекци-
ям точки всегда можно построить
ее третью ортогональную проек-
цию. При построении третьей про-
екции точки необходимо учиты-
вать, что при ортогональном про-
ецировании проекции точки на
эпюре расположены на линиях свя-
зи, перпендикулярных осям x, y
или z
:
А
1
А
2
⊥ x;
А
2
А
3
⊥ z;
А
1
А
3
⊥ y; (распадается на два от-
резка [А
1
А
y
] ⊥
у ⊂ π
1
и
[А
3
А
y
]
⊥
y ⊂ π
3
).
A
x
A
1
A
2
y
Î
z
x
y
A
3
A
z
y
y
Рис. 22

30
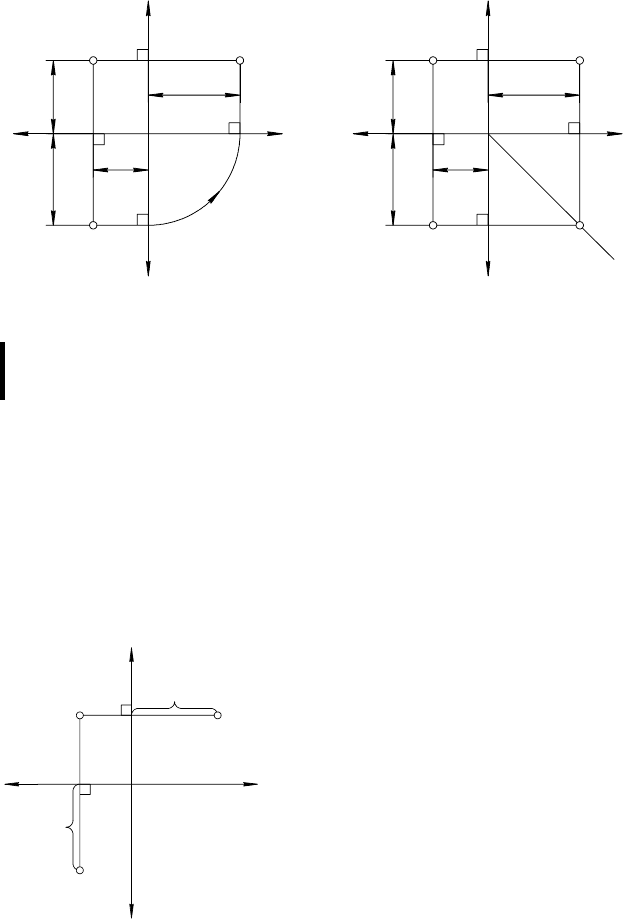
Чаще всего строят профильную проекцию фигуры, а, зна-
чит, и профильные проекции точек, ей принадлежащих. При
этом неоднократно повторяются одни и те же построения, ко-
торые можно представить в виде следующего алгоритма
(рис. 22):
1. Через фронтальную проекцию точки провести линию связи
перпендикулярно оси z
(А
2
А
3
) ⊥
z
2. Замерить расстояние, равное ординате точки, и отложить
его (с учетом знака) от оси z по проведенной линии связи
y = [А
1
А
x
] = [А
z
А
3
]
2.3. КОНКУРИРУЮЩИЕ ТОЧКИ
Точки в пространстве могут либо совпадать, либо не совпа-
дать (см. табл. 1 и 5, 1.3.). Если точки в пространстве совпадают
(А ≡ В), то на эпюре их одноименные проекции совпадают
А
1
≡ В
1
, А
2
≡ В
2
(рис. 44).
G
2
≡
( H
2
)
H
1
G
1
A
2
≡
B
2
C
1
A
1
≡
B
1
x
C
2
D
1
D
2
F
2
E
2
( F
1
)
≡
E
1
O
Рис. 23
У двух различных точек в пространстве не совпадает хотя бы
одна пара одноименных проекций. На рис. 23 даны проекции
точек C, D, E, F, G и H, которые в пространстве не совпадают
одна с другой. У точек C и D различны обе пары одноименных
проекций, а точки E, F и G, H
имеют пару совпавших одно-
именных проекций.
Точки, имеющие одну пару совпавших одноименных проекций,
называются конкурирующими.
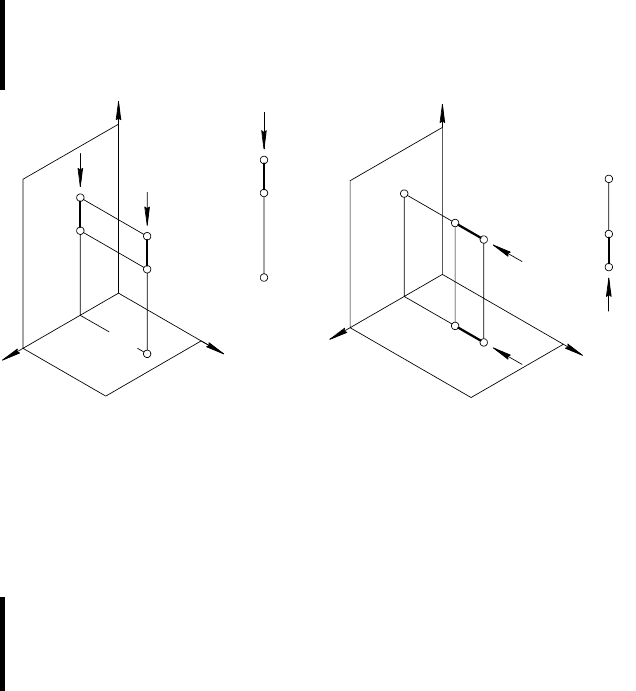
31
Если совпадают горизонтальные проекции точек E
1
и
F
1
(рис. 23), то точки E и F называют горизонтально конкури-
рующими. Точки G и H называют фронтально конкурирующими,
так как G
2
≡ H
2
(рис. 23).
Конкурирующие точки расположены на проецирующих лу-
чах: (EF ] ⊥ π
1
, а (GH ] ⊥ π
2
. С помощью
конкурирующих точек
определяют видимость на чертежах.
С помощью горизонтально конкурирующих точек А и В
(рис. 24) решают вопрос о взаимной видимости горизонтальных
проекций точек на эпюре, т. е. видна А
1
или В
1
. Для решения
вопроса обращаются к фронтальным проекциям точек:
Если на эпюре заданы горизонтально конкурирующие точки, то
видна горизонтальная проекция той точки, у которой фронталь-
ная проекция расположена выше.
Î
p
2
x
y
z
p
3
p
1
Î
x
y
z
D
D
1
D
2
≡
( C
2
)
p
2
p
1
C
C
1
B
2
B
A
2
A
B
2
A
2
A
1
≡
( B
1
)
C
1
D
1
A
1
≡
( B
1
)
D
2
≡
( C
2
)
Рис. 24 Рис. 25
Проекцию невидимой точки условно заключают в скобки.
На рис. 24 видна А
1
, так как А
2
выше B
2
, а значит, в простран-
стве точка А выше точки В и ее проекция А
1
закрывает проек-
цию В
1
.
На рис. 25 определена видимость фронтальных проекций
точек С и D.
У двух фронтально конкурирующих точек на эпюре видна
фронтальная проекция той точки, у которой горизонтальная
проекция расположена ниже.
