Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.


12
В проективном пространстве (SB)
I
π
1
=
∞1
B (рис. 1) и, сле-
довательно, фиксированный аппарат проецирования (S
∧
π
1
) по-
зволяет строить проекции для любой точки этого пространства.
Таким образом, любая проекция представляет собой геометри-
ческое место (множество) точек пересечения проецирующих
лучей с плоскостью.
1.4.1. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Метод центрального проецирования — общий случай метода
проекций. Аппарат проецирования этого метода был рассмотрен
в 1.4. (рис. 1). S — центр проецирования является собственной
точкой пространства. A
1
— центральная проекция точки A на
плоскость π
1
. Для любой точки A центральную проекцию строят
по следующему алгоритму:
1. A U S = ( AS )
2. (AS ) I π
1
= A
1
Так как через две различные точки (A и S ) проходит единст-
венная прямая, можно сделать вывод: при заданном аппарате
проецирования каждая точка пространства имеет только одну
центральную проекцию.
Обратное утверждение (каждой центральной проекции точки
однозначно соответствует точка в пространстве) не имеет места.
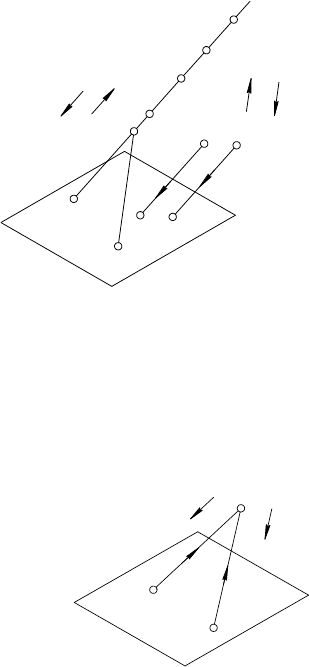
Из рис. 1 видно, что точка A
1
может быть центральной про-
екцией точек A, A
1
, A
2
, A
3
,…A
n
, принадлежащих прямой (AS ).
Поэтому одна центральная проекция точки не определяет по-
ложения самой точки в пространстве.
Чтобы определить положение точки необходимо иметь две
ее центральные проекции, полученные при проецировании этой
точки из двух различных центров S и S
/
(рис. 1). Имея две цен-
тральные проекции A
1
и
/
1
A можно определить положение точ-
ки A в пространстве. Для этого достаточно провести прямые
(A
1
S ) и (
/
1
A S
/
) и отметить точку их пересечения:
( A
1
S ) I (
/
1
A
S
/
) = A.
На рис. 1 показано также определение точки C по ее цен-
тральным проекциям
1
C и
/
1
C .
13
1.4.2. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Параллельное проецирование является частным случаем
центрального проецирования, когда центр проекций помещен в
несобственную точку
∞
S . Положение несобственной точки за-
дают направлением s (рис. 3).
Проекция определяется по тому же алгоритму, что и в слу-
чае центрального проецирования:
1. A
U
∞
S = (A
∞
S ) ∨ (AA
1
) || s
;
2. (A
∞
S ) I π
1
= A
1
∨ (AA
1
) I π
1
= A
1
.
Соединить точку A с цен-
тром
∞
S — значит провести
прямую AA
1
параллельную на-
правлению s.
Очевидно, что при таком
расположении центра проек-
ций все проецирующие прямые
будут параллельны между со-
бой (BB
1
) || (CC
1
) ||…|| (A
∞
S )
||
s,
так как имеют общую несобст-
венную точку, совпадающую с
центром проекций.
Параллельность проеци-
рующих прямых определяет
название — параллельное про-
ецирование, а полученные с его помощью проекции — парал-
лельными проекциями.
Являясь частным случаем центрального проецирования, па-
раллельное проецирование сохраняет все его свойства, поэтому
каждая точка пространства при заданном аппарате проецирова-
ния
будет иметь только одну парал-
лельную проекцию.
Обратное утверждение, как и в
случае центрального проецирования,
места не имеет, так как точка A
1
(рис. 3) может быть параллельной
проекцией любой точки A
1
, A
2
,
A
3
… A
n
, принадлежащей прямой
(A
1
∞
S ).
Для определения положения точки
в пространстве необходимо иметь две
Рис. 3
p
1
B
B
/
1
s
s
/
B
1
Рис.4
p
1
A
A
/
1
S
È
A
1
s
A
1
A
3
A
2
A
n
S
/
È
s
/
B
1
C
1
B
C
14
ее параллельные проекции, полученные при двух различных на-
правлениях проецирования.
Положение точки A (рис. 3) определяется пересечением
прямых, проведенных через A
1
и
/
1
A параллельно соответст-
вующим направлениям s и s
/
. На рис. 4 показано построение в
пространстве точки В по известным ее параллельным проекци-
ям В
1
и
/
1
B .
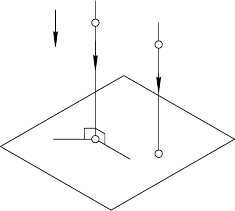
1.4.3. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Параллельное (косоугольное) проецирование называется
прямоугольным или ортогональным (от слова orthoqonios — пря-
моугольный, если направление проецирования перпендикуляр-
но плоскости проекций (s ⊥ π
1
рис. 5).
Прямоугольную (ортогональную)
проекцию точки строят по известному
алгоритму (см. 1.4.2.):
1. (AA
1
)
⊥ π
1
;
2. (AA
1
) I π
1
= A
1
.
Как уже отмечалось, (см. 1.4.2.),
положение точки в пространстве оп-
ределяют две ее параллельные проек-
ции. Через точку можно провести
только одну прямую, перпендикуляр-
ную к плоскости, поэтому для полу-
чения двух проекций одной точки
при ортогональном проецировании
вводят вторую плоскость проекций
π
2
(π
2
= π
1
) (рис. 6).
При ортогональном проецировании плоскости проекций π
1
и π
2
располагают перпендикулярно друг другу (π
1
⊥π
2
).
Множество точек пространства {A, B, C, …} проецируют ор-
тогонально на обе плоскости проекций. Множество
{A
1
, B
1
, C
1
, …} образует поле проекций плоскости π
1
, называемое
горизонтальной плоскостью проекций, а множество
{A
2
, B
2
, C
2
, …} — поле проекций плоскости π
2
, называемое фрон-
тальной плоскостью проекций.
При фиксированном положении плоскостей π
1
и π
2
каждой
точке пространства A соответствует упорядоченная пара точек
(A
1
, A
2
) на полях проекций: A ⇒ (A
1
, A
2
).
p
1
B
B
1
A
A
1
s
Рис. 5

15
Справедливо и обратное утвержде-
ние — упорядоченной паре точек полей
проекций соответствует единственная
точка пространства (A
1
, A
2
) ⇒ A, т. е.
A ⇔ (A
1
, A
2
).
Отмеченное свойство ортогонально-
го проецирования лежит в основе по-
строения чертежа, так как обеспечивает
его обратимость и простоту графиче-
ских построений (см. 1.4.).
Ортогональное проецирование ши-
роко применяется в технике при вы-
полнении машиностроительных черте-
жей.
1.5. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО
ПРОЕЦИРОВАНИЯ
При проецировании оригинала на плоскость одни его части
искажаются по форме и размерам, а другие — и на проекции
остаются без изменения. Например, прямая линия при проеци-
ровании на плоскость остается прямой; точка, лежащая на пря-
мой, проецируется в точку, лежащую на проекции той же пря-
мой и т. д.
Свойства оригинала
, которые не изменяются в процессе
проецирования, называют независимыми или инвариантными
(инварианты) относительно выбранного способа проецирования.
Чем больше количество инвариантов имеет метод проециро-
вания, тем проще построение проекций, удобнее осуществление
процесса обратимости чертежа.
Инвариантные свойства имеет любой из способов проециро-
вания. Эти свойства являются опорными при выявлении гео-
метрической характеристики изображенного пространственного
объекта.
Рассмотрим инвариантные свойства ортогонального (прямо-
угольного) проецирования:
1. Проекция точки есть точка:
A → A
1
Рис.6
p
2
p
1
B
B
1
A
A
2
B
2
A
1
16
2. Если фигура Ф
1
принадлежит фигуре Ф
2
, то проекция фигу-
ры Ф
1
принадлежит проекции фигуры Ф
2
:
Ф
1
⊂ Ф
2
⇒
1
2
Ф ⊂
2
1
Ф
Это свойство называют свой-
ством инцидентности (см. 1.3.,
табл. 3).
Свойство 1 следует из по-
строения проекций точки
(см. 1.4.). Через каждую точку A
проходит единственная прямая
(AA
1
), которая пересекает плос-
кость проекций π
1
в единствен-
ной точке A
1
(рис. 5).
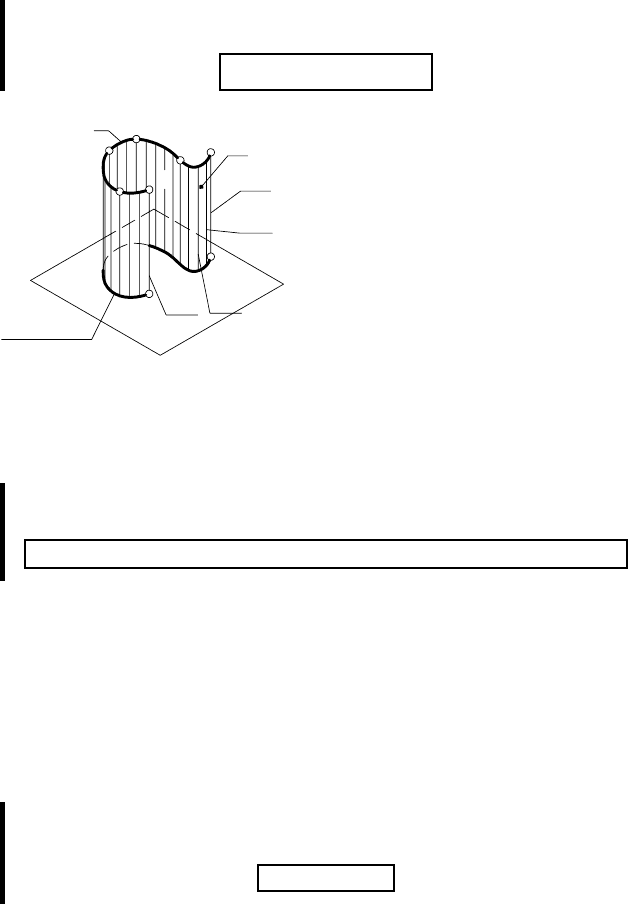
При проецировании линии l,
проецирующие лучи проходящие
через каждую из ее точек, обра-
зуют поверхность α
{а
1
, а
2
,а
3
, … а
n
}, называемую проецирующей
(рис. 7).
Из свойства 1 имеем:
1 а. Проекция проецирующей поверхности есть линия пересечения
этой поверхности с плоскостью проекций:
α{a
1
, a
2
, a
3
, … a
n
} ∧ (a
1
||, a
2
||, a
3
||,…|| a
n
⊥π
1
) ⇒ α
1
= α I π
1
= h
0
α
Проекция проецирующей поверхности α
1
(рис. 7), представ-
ляющая собой геометрическое место (множество) точек пересе-
чения проецирующих лучей с плоскостью π
1
(см. 1.4.), принад-
лежит и поверхности α и плоскости π
1
, т. е. α
1
= α I π
1
.
Линия пересечения плоскости (поверхности) с плоскостью
проекций называется ее следом (см. 1.3.). В данном случае h
0
α
—
горизонтальный след поверхности α, который совпадает с ее,
вырожденной в линию, горизонтальной проекцией:
h
0
α
=
α
I
π
1
=
α
1
.
1 б. Проекция прямой на плоскость есть прямая линия, в частном
случае (когда прямая перпендикулярна плоскости) — точка.
l → l
1
∨ → H
1
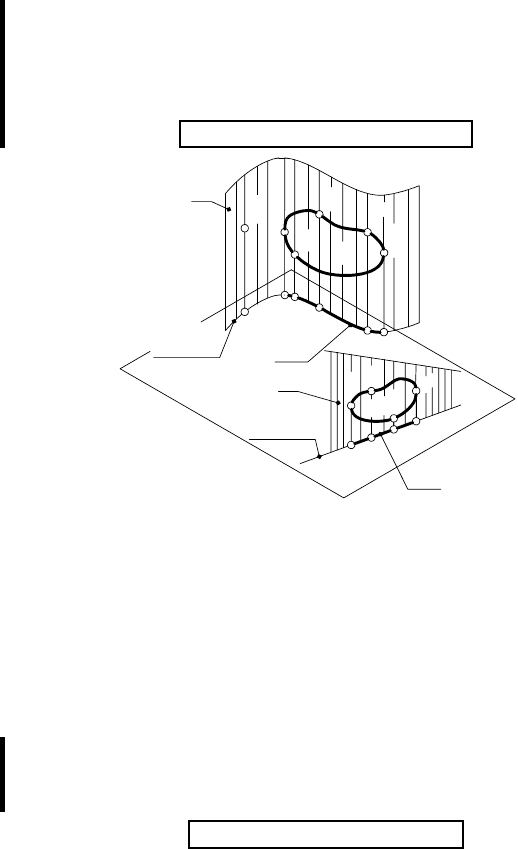
При проецировании прямой линии (AВ ) (рис. 8) проеци-
рующие лучи образуют плоскость α. Из свойства 1а следует:
α
1
= α I π
1
, но две плоскости пересекаются по прямой, поэтому
α
1
— прямая.
Рис. 7
p
1
A
A
1
B
1
B
a
a
1
≡
h
O
a
≡
l
1
a
1
a
2
a
3
a
n
l
17
Из свойства 2 имеем:
2 а. Если фигура Ф принадлежит плоскости α, перпендикулярной
плоскости проекций π
1
(или проецирующей поверхности α), то
проекция этой фигуры принадлежит соответствующему следу
плоскости α (или проецирующей поверхности α):
(Ф ⊂ α)
∧
(α ⊥ π
1
) ⇒
Ф
1
⊂ h
0
α
p
1
E
P
P
1
E
1
C
1
B
1
C
B
a
1
≡
h
O
a
C
E
B
K
A
P
B
1
P
1
K
1
A
1
C
1
E
1
Ô
1
Ô
a
a
Ô
Ô
1
a
1
≡
h
O
a
Рис. 9
В данном случае (рис. 9), π
1
— горизонтальная плоскость
проекций, следовательно, соответствующий след плоскости α —
горизонтальный (h
0
α
).
Из свойства 1а:
(Ф ⊂ α) ∧ (α ⊥ π
1
) ⇒ Ф
1
⊂ α I π
1
= h
0
α
,
следовательно:
(Ф ⊂α) ∧ (α⊥π
1
) ⇒ Ф
1
⊂ h
0
α
.
2 б. Если фигура Ф принадлежит плоскости α, параллельной
плоскости проекций π
1
, то проекция этой фигуры Ф
1
на плос-
кость π
1
конгруэнтна самой фигуре.
(Ф ⊂ α) ∧ (α || π
1
) ⇒ Ф
1
≅ Ф
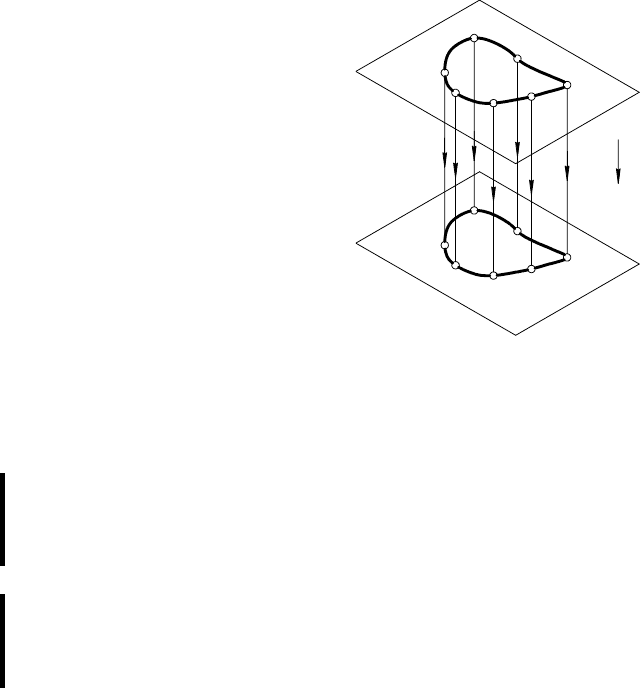
18
Действительно, пусть α || π
1
и
Ф ⊂ α, а Ф
1
— ортогональная
проекция Ф (рис. 10). При дви-
жении плоскости α параллельно
самой себе по направлению
s ⊥ π
1
, на расстояние | AA
1
| фигу-
ры Ф и Ф
1
совместятся всеми
своими точками, так как
|AA
1
| = |BB
1
| = |СС
1
| = … = |NN
1
| =
= | απ
1
|, как отрезки параллельных
прямых, заключенные между па-
раллельными плоскостями. Фигу-
ры, совпадающие при совмеще-
нии всеми своими точками со-
гласно определению (см. 1.3.)
конгруэнтны, т. е. Ф
≅
Ф
1
.
Свойства ортогонального проецирования лежат в основе
решения задач начертательной геометрии. Множество всех за-
дач, решаемых графическим путем, условно можно разделить на
позиционные и метрические.
Позиционными называют задачи, в результате решения которых
можно получить ответ на вопрос об инцидентности заданных
геометрических фигур.
Метрическими называют задачи, решение которых связано с на-
хождением линейных и угловых характеристик геометрических
фигур.
Решение позиционных задач базируется на инвариантном
свойстве 2 ортогонального проецирования, а решение метриче-
ских задач на свойстве 2б.
1.6. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Аксонометрические изображения широко применяются бла-
годаря хорошей наглядности и простоте построений.
Слово «аксонометрия» в переводе с греческого означает из-
мерение по осям. Аксонометрический метод может сочетаться и
с параллельным, и центральным проецированием при условии,
что предмет проецируется вместе с координатной системой.
p
1
B
1
A
1
C
1
a
D
1
E
1
N
1
M
1
B
A
C
D
E
N
M
Ô
1
Ô
s
Рис. 10
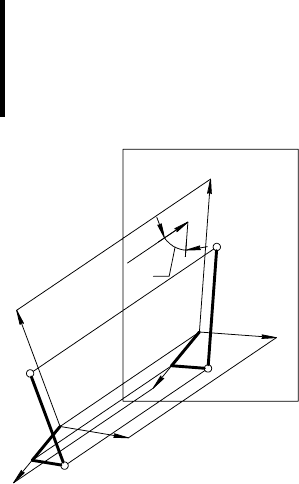
19
Сущность метода параллельного аксонометрического проециро-
вания заключается в том, что предмет относят к некоторой
системе координат и затем проецируют параллельными лучами
на плоскость вместе с координатной системой.
На рис. 11 показана точка A,
отнесенная к системе прямо-
угольных координат xyz, s опре-
деляет направление проециро-
вания на картинную плос-
кость π
0
(плоскость аксономет-
рических проекций).
Для создания аксонометри-
ческой (в нашем случае парал-
лельной) проекции точки A
проведем через нее проеци-
рующий луч (параллельный на-
правлению s) и найдем пересе-
чение его с плоскостью π
0
в
точке A
0
. Это построение пока-
зывает, что при заданном на-
правлении проецирования каж-
дой точке A пространства на
плоскости проекций соответст-
вует определенная точка A
0
.
Но обратно, как известно, утверждать нельзя. Действитель-
но, каждой точке A
0
на плоскости π
0
соответствует любая точка
проецирующего луча (A
0
A].
Для того чтобы устранить эту неопределенность и обеспе-
чить взаимную однозначность между точками пространства и
точками картинной плоскости, поступают следующим образом:
на плоскость π
0
проецируют не только точку A, но и одну из ее
ортогональных проекций (обычно горизонтальную проек-
цию A
1
).
Аксонометрическую проекцию
0
1
A горизонтальной проекции
точки A принято называть вторичной проекцией. Этот термин
хорошо выражает тот факт, что точка
0
1
A
получается в результа-
те двух последовательных проецирований.
Рассмотрев рис. 11, можно сделать вывод о том, что если за-
даны система координат xyz, направление проецирования s и
плоскость π
0
, то аксонометрическая проекция точки и ее вторич-
Рис. 11
Î
x
y
z
A
1
A
Î
0
z
0
A
0
x
0
A
0
1
y
0
p
0
s
f

20
ная проекция однозначно определяют положение точки в про-
странстве. Действительно, проведя через вторичную проекцию
0
1
A точки A прямую, параллельную s и определив точку пересе-
чения этой прямой с координатной плоскостью xOy найдем го-
ризонтальную проекцию A
1
точки A. Положение же точки A в
пространстве определяется пересечением двух прямых A
0
A и
A
1
A, первая из которых проходит через A
0
параллельно s, а вто-
рая — через A
1
перпендикулярно плоскости xOy.
На плоскости картины π
0
(рис. 11) показана и аксонометри-
ческая проекция осей координат — плоская система x
0
y
0
z
0
. В
общем случае длина отрезков осей координат в пространстве не
равна длине их проекций.
Искажение отрезков осей координат при их проецировании
на плоскость π
0
характеризуется, так называемым, коэффициен-
том искажения.
Коэффициентом искажения называется отношение длины аксо-
нометрической проекции отрезка оси к его истинной длине.
Так, коэффициент искажения по оси x
0
:
0
x
K
Ох
хО
00
=
, по
оси y
0
:
0
y
K
,
Оy
yО
00
=
и по оси z
0
:
0
z
K
Оz
zО
00
=
(см. рис. 11).
В зависимости от соотношения коэффициентов искажения
аксонометрические проекции могут быть:
1) изометрическими, если коэффициенты искажения по
всем трем осям равны между собой; в этом случае
000
zyx
KKK ==
;
2) диметрическими, если коэффициенты искажения по двум
любым осям равны между собой, а по третьей — отличаются от
первых двух;
например,
000
zyx
KKK
=
=
;
3) триметрическими, если все три коэффициента искажения
по осям различны, т.е. когда
000
zyx
KKK
=
=
.
Аксонометрические проекции различаются также и по тому
углу ϕ (рис. 11), который образуется проецирующим лучом с
плоскостью проекций π
0
. Если ϕ° = 90°, то аксонометрическая
проекция называется косоугольной, а если ϕ° = 90° — прямо-
угольной.

21
Естественно, что изометрические, диметрические и тримет-
рические проекции могут быть как прямоугольными, так и ко-
соугольными.
Зная коэффициент искажения и
свойства взаимного расположения
точек, линий и плоских фигур, ко-
торые сохраняются при их парал-
лельном проецировании можно по-
строить аксонометрическое изобра-
жение точки A. Это изображение
определяется как граничная точка
координатной ломаной, состоящей
из отрезков
0
A
x
,
0
A
y
,
0
A
z
, отложен-
ных от начала аксонометрических
осей О
0
на соответствующих прямых
параллельных этим осям (рис. 12)
или совпадающих с ними:
00
1
00
0
AAAO
x
.
Построение координатной ломаной требует измерения трех
прямоугольных координат точки x, y, z, перевода их при помо-
щи коэффициентов искажения в аксонометрические и вычерчи-
вания этой ломаной, при построении которой попутно строится
и одна из вторичных проекций
0
1
A
точки A.
Основная теорема аксонометрии
При построении параллельной аксонометрической проекции
можно произвольно выбрать плоскость проекций π
0
и направ-
ление проецирования. Очевидно, любое изменение взаимного
положения осей координат и плоскости проекций и всякое из-
менение положения аксонометрических осей вызовет как изме-
нение положения аксонометрических осей, так и коэффициен-
тов искажения по ним.
Геометр XIX века К. Польке в 1853 г., изучая вопрос о том,
в какой зависимости находятся направления
аксонометрических
осей и коэффициенты искажения по ним от направления про-
ецирования и положения плоскости проекций, пришел к сле-
дующему выводу.
Теорема Польке. Три произвольно выбранных отрезка
Ο
0
х
0
, О
0
y
0
,
О
0
z
0
на плоскости π
0
, выходящие из одной точки, представляют
Рис. 12
Î
0
x
0
y
0
z
0
A
0
1
A
0
x
0
A
z
0
A
y
0
A
A
0
x
0
