Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.

32
2.4. ПРОЕЦИРОВАНИЕ ПРЯМОЙ ЛИНИИ
Согласно известной аксиоме евклидовой геометрии через
две различные точки проходит единственная прямая, поэтому
на эпюре прямую можно задать проекциями двух принадлежа-
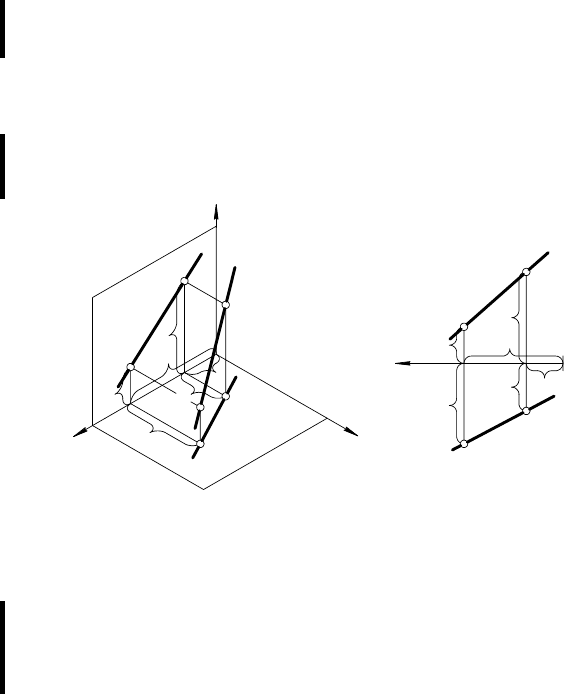
щих ей точек. На рис. 26, а заданы точки А
(А
1
, А
2
) и В
(В
1
, В
2
),
принадлежащие прямой l. Соединив одноименные проекции
точек, получим проекции прямой l
1
и l
2
:
А
1
U В
1
= А
1
В
1
= l
1
;
А
2
U В
2
= А
2
В
2
= l
2
;
Эпюром прямой называется чертеж, состоящий из двух или
более ее ортогональных проекций, связанных между собой.
На основании инвариантного свойства 1 б (см. 1.5) проек-
ция прямой в общем случае есть прямая, поэтому прямую мож-
но задать двумя ее проекциями а (а
1
, а
2
) рис. 26.
Точка пересечения прямой с плоскостью проекций называется ее
следом.
A
1
A
2
Î
x
Î
p
2
x
y
z
p
1
B
A
1
B
2
ó
A
z
A
B
1
l
1
l
2
l
A
z
B
x
B
ó
B
x
A
A
2
B
2
B
1
l
2
l
1
ó
A
ó
B
x
B
x
A
z
B
z
A
а б
Рис. 26
На рис. ?? построены следы прямой b: горизонтальный след
Н
b
= b I π
1
и фронтальный след F
b
= b I π
2
.
Прямая, наклоненная к плоскостям проекций π
1
, π
2
и π
3
под про-
извольными углами (отличными от 0
° и 90
°), называется прямой
общего положения.
На эпюре проекции прямой общего положения наклонены к
оси х под углами, не равными 0° или 90° (рис. 26, 27).
33
a
2
a
1
Рис. 27
Прямую называют восходящей, если по мере удаления от наблю-
дателя она повышается.
На эпюре проекции восходящей прямой направлены в одну
сторону (ориентированы одинаково). На рис. 26 даны проекции
восходящей прямой.
Прямая называются нисходящей, если по мере удаления от на-
блюдателя она понижается.
На эпюре проекции нисходящей прямой направлены в раз-
ные стороны (ориентированные противоположно). Прямая
а (а
1
, а
2
) на рис. 27 — нисходящая.
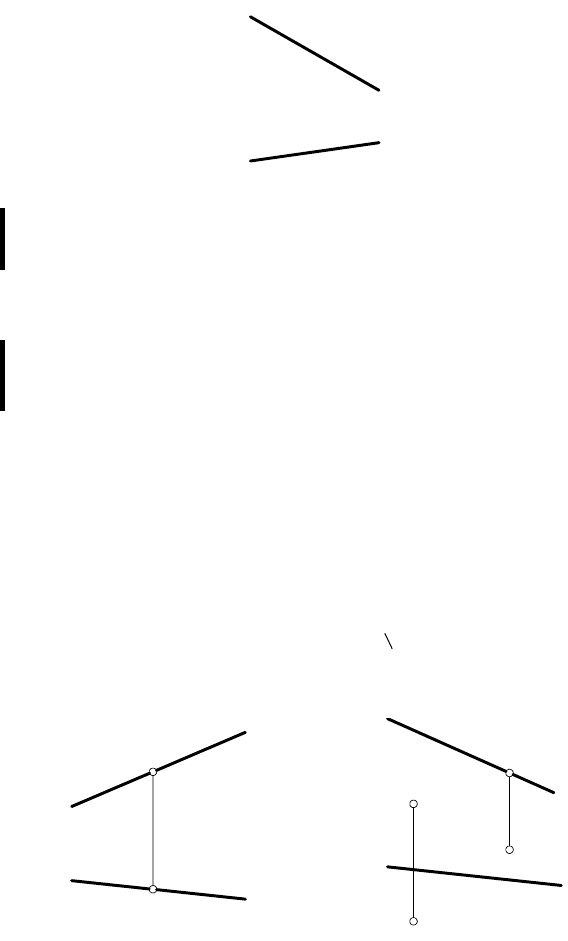
2.5. ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПРЯМОЙ ЛИНИИ
Возможны два случая взаимного расположения точки и
прямой (см. 1.3., табл. 5):
— точка принадлежит прямой А ∈ l (рис. 28).
— точка не принадлежит прямой А ∈ l (рис. 29).
Если в пространстве точка А принадлежит прямой l
,
то, согласно инвариантному свойству ортогонального проециро-
l
2
l
1
A
1
A
2
l
2
l
1
B
1
B
2
A
1
A
2
Рис. 28 Рис. 29
34
вания 2 (см. 1.5.), ее проекции на эпюре принадлежат одно-
именным проекциям прямой (рис. 28):
⎩
⎨
⎧
∈
∈
⇔∈
.
;
22
11
lA
lA
lA
Если хотя бы одна из проекций точки не принадлежит од-
ноименной проекции прямой, то данная точка в пространстве
не принадлежит прямой (рис. 29):
⎩
⎨
⎧
∈
∈
⇔∈
.
;
22
11
lA
lA
lA
⎩
⎨
⎧
∈
∈
⇔∈
.
;
22
11
lB
lB
lB
2.6. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ
Прямые в пространстве могут занимать относительно плос-
костей проекций общее положение (см. 2.4.) или частное поло-
жение.
Прямой частного положения (относительно плоскостей проек-
ций) называют прямую параллельную или перпендикулярную од-
ной из плоскостей проекций.
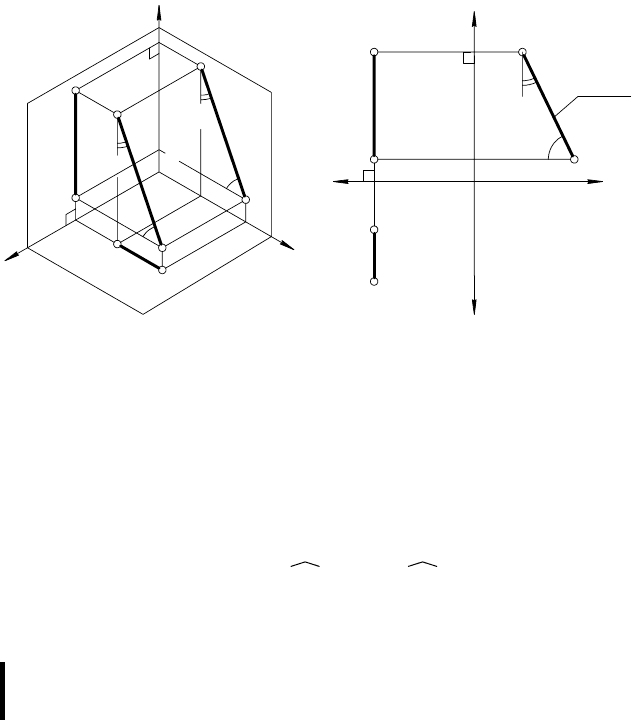
Прямые уровня
Прямая параллельная одной из плоскостей проекций, называется
прямой уровня.
Прямых уровня три вида:
а) горизонталь h
||
π
1
(рис. 30, а и б
);
Фронтальная проекция h
2
любой горизонтали h параллельна
оси x (рис. 30, а) или (в безосной системе) перпендикулярна
вертикальной линии связи (рис. 30, б
). Проецирующая плос-
кость горизонтали АА
2
В
2
В параллельна плоскости проекций π
1
(рис. 30, а). Согласно инвариантному свойству 2
б (см. 1.5.), от-
резок [АВ
] горизонтали h и углы ее наклона β° = h π
2
и γ° = h π
3
проецируются на плоскость проекций
π
1
, в натуральную вели-
чину
(рис. 30,
б
).
б) фронталь f
||
π
2
(рис. 31, а и б
);
35
A
1
A
2
Î
p
2
x
y
z
p
1
B
B
2
B
1
h
2
h
1
B
1
A
2
A
1
A
h
2
b Å
b Å
g Å
g Å
g Å
|
A B
|
h
1
h
b Å
B
2
а б
Рис. 30
Проецирующая плоскость АА
1
В
1
В фронтали f (рис. 31, а) па-
раллельна плоскости проекций π
2
, а [АВ ] ∈ f (рис. 31, б
) про-
ецируется на π
2
в натуральную величину: |
АВ | = |
А
2
В
2
|
(см. свойство 2 б, 1.5.). Углы наклона фронтали к плоскостям
проекций π
1
и π
2
на основании того же свойства проецируются
на π
2
без искажения: α° = f π
1
; β° = f π
2
. У любой фронтали го-
ризонтальная проекция f
1
параллельна оси х (рис. 31, а) или
перпендикулярна вертикальной линии связи (рис. 31, б
).
A
1
A
2
B
2
B
1
g Å
|
A B
|
a Å
p
2
p
1
B
B
1
A
2
A
1
A
g Å
f
1
B
2
a Å
a Å
z
y
x
f
2
f
Î
g Å
f
1
f
2
а б
Рис. 31
36
в) профильная прямая (АВ)
||
π
3
(рис. 32, а и б
).
Î
p
2
x
y
z
p
1
B
B
1
A
2
A
1
A
b Å
a Å
B
2
b Å
a Å
A
3
B
3
A
1
A
2
B
2
B
1
b Å
|
A B
|
a Å
y
z
x
y
Î
B
3
A
3
а б
Рис. 32
Горизонтальная и фронтальная проекции профильной пря-
мой совпадают с направлением вертикальных линий связи
(рис. 32, б
). Проецирующие плоскости А
1
АВВ
1
и А
2
АВВ
2
совпа-
дают (А
1
АВВ
1
= А
2
АВВ
2
) и образуют одну плоскость параллель-
ную плоскости π
3
(рис. 32, а). По свойству 2 б (см. 1.5.) отрезок
профильной прямой [АВ] и углы наклона этой прямой к плос-
костям проекций π
1
и π
2
проецируются на π
3
в натуральную ве-
личину:
|А
3
В
3
| = | АВ |; α° = AB π
1
; β° = AB π
2
(рис. 32, б
).
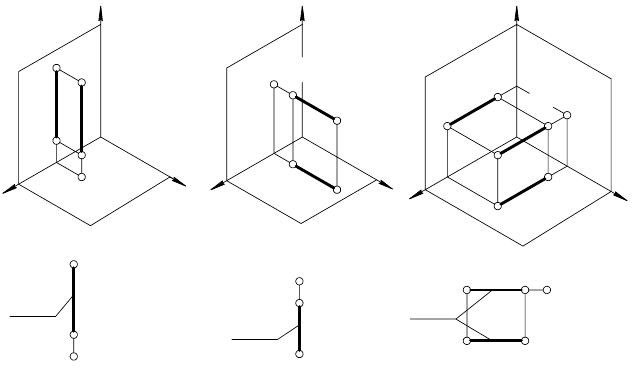
Проецирующие прямые
Прямая, перпендикулярная одной из плоскостей проекций, назы-
вается проецирующей прямой.
Проецирующих прямых три вида:
а) горизонтально проецирующая прямая i ⊥
π
1
(рис. 33, а и б ).
Все свои точки прямая i проецирует в одну точку на плоскость
π
1
(i
1
— вырожденная в точку проекция прямой i
).
На рис. 33, б i
1
≡ А
1
≡ В
1
≡ H
i
, где H
i
— горизонтальный след
(см. 2.4.) прямой i: H
i
= i I
π
1
. На фронтальную плоскость про-
екций отрезок этой прямой проецируется без искажения
|
А
2
В
2
| = |
АВ |;
37
Î
p
2
x
y
z
p
1
B
A
2
A
1
≡
B
1
≡
i
1
≡
H
i
A
B
2
A
1
A
2
B
2
B
1
Î
p
2
x
y
z
p
1
x
y
z
p
1
B
A
2
A
3
≡
B
3
≡
i
3
≡
P
3
A
A
1
B
1
i
i
1
i
2
i
A
B
A
2
≡
B
2
≡
i
2
≡
F
i
Î
i
2
B
2
i
i
1
p
2
A
1
B
1
A
1
≡
B
1
≡
i
1
≡
H
i
|
A B
|
i
2
A
2
B
2
A
2
≡
B
2
≡
i
2
≡
F
i
|
A B
|
B
1
A
1
A
3
≡
B
3
≡
i
3
≡
P
3
i
1
i
1
i
2
|
A B
|
a
б б
a
б
a
Рис. 33 Рис. 34 Рис. 35
б) фронтально проецирующая прямая i ⊥ π
2
(рис. 34, а и б
).
Все точки этой прямой на π
2
проецируются в одну (вырожден-
ная в точку проекция прямой): i
2
≡ A
2
≡ B
2
≡ F
i
,
где F
i
— фронталь-
ный след прямой i : F
i
= i I
π
2
. Горизонтальная проекция любо-
го отрезка фронтально проецирующей прямой равна длине са-
мого отрезка: | А
1
В
1
| = | АВ |;
в) профильно проецирующая прямая i ⊥ π
3
(рис. 35, а и б
).
Профильная проекция прямой i
3
совпадает с профильными
проекциями всех принадлежащих ей точек (вырождается в точ-
ку): i
3
≡ A
3
≡ B
3
≡ P
i
, где P
i
— профильный след прямой: P
i
= i I π
3
.
Фронтальная и горизонтальная проекции любого отрезка про-
фильно проецирующей прямой равны между собой, а их длина
равна длине самого отрезка: | А
2
В
2
| = | А
1
В
1
| = | АВ |.
На проецирующих прямых лежат конкурирующие точ-
ки (см. 2.3.).
2.7. ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА
ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ
Отрезки прямых, занимающих частное положение относи-
тельно плоскостей проекций, проецируются в натуральную ве-
личину хотя бы на одну из плоскостей проекций (см. 2.6.) Отре-
зок прямой общего положения проецируется с искажением на
любую плоскость проекций. Зависимость длины проекции тако-
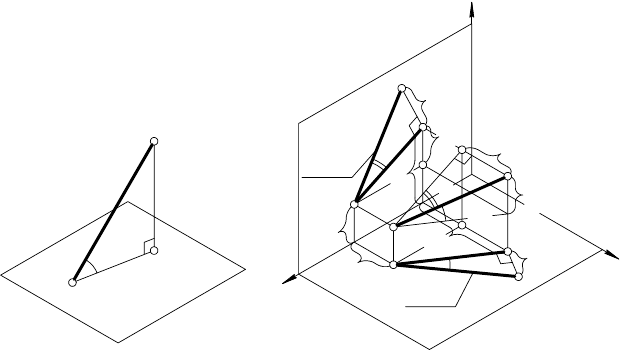
38
го отрезка от его истинной величины может быть выражена из
прямоугольного треугольника АBB
1
(рис. 36): | А
1
В
1
| =
= | АВ |
·
cos
α. Угол α — угол наклона отрезка АB к плоскости π
1
(в курсе элементарной геометрии углом наклона прямой к
плоскости называют угол, образованный этой прямой и
ее ортогональной проекцией на данную плоскость, т. е.
α° = ВА
1
В
1
).
B
B
1
A
≡
A
1
a Å
p
1
y
x
z
A
2
B
2
A
1
B
B
0
|
A B
|
|
A B
|
B
|
1
D
y
B
|
D
y =
|
y
B
- y
A
|
z
A
B
0
D
z =
|
z
B
- z
A
|
B
| |
a Å
B
| |
2
y
B
y
A
p
1
b Å
A
a Å
p
2
D
z
b Å
B
1
D
z
z
B
Рис. 36 Рис. 37
Величина фронтальной проекции отрезка |
А
2
В
2
| = |
АВ |
·
cos
β
(рис. 37), где β° — угол наклона отрезка [АВ] к плоскости про-
екций π
2
, а | А
3
В
3
|
=
| АВ |
·
cos
γ, где γ°
— угол наклона пря-
мой
(АВ
]
к
плоскости
проекций
π
3
.
В начертательной геометрии натуральную величину отрезка
и углов его наклона к плоскостям проекций π
1
, π
2
и π
3
опреде-
ляют построением.
Пусть в пространстве задан отрезок АВ
(рис. 37). Построим
его ортогональные проекции
[А
1
В
1
] и [А
2
В
2
]
на плоскости про-
екций π
1
и π
2
. В проецирующей плоскости А
2
В
2
ВА через точку А
проведем [АВ
/
] параллельно А
2
В
2
. Получим прямоугольный
UАВ
/
В. Угол АВ
/
В — прямой, так как (ВВ
2
] ⊥
π
2
, а
[АВ
/
] ||
[А
2
В
2
]
. В UАВ
/
В гипотенуза является натуральной вели-
чиной [АВ ], катет [АВ
/
] равен | А
2
В
2
|, так как А
2
В
2
В
/
А — прямо-
угольник (стороны попарно параллельны и все углы прямые); а
катет [ВВ
/
] равен разности расстояний концов отрезка [АВ ] до

39
плоскости проекций π
2
, т. е. разности ординат точек А и В:
|
/
1
1
BB
| = | y
А
— y
В
| = ∆y
.
На эпюре длины катетов легко определить: | АB
/
| = | А
2
B
2
| и
|
/
BB
| = |
/
1
1
BB
|. По двум катетам строят UА
2
В
2
В
0
с прямым углом
в точке В
2
(или А
2
) и определяют натуральную величину отрезка
[АВ] как гипотенузу | А
2
В
0
|. Угол β° между гипотенузой и проек-
цией [А
2
В
2
] — угол наклона прямой (АВ) к плоскости проек-
ций π
2
.
Натуральную величину отрезка [АВ] и угол
α
его наклона к
плоскости π
1
определяют на эпюре с помощью его горизонталь-
ной проекции [А
1
В
1
] (рис. 37), являющейся одним катетом пря-
моугольного UА
1
В
1
В
0
, равного UАВВ
//
. Тогда второй ка-
тет [В
1
В
0
] равен разности расстояний концов отрезка [АВ] до
плоскости π
1
, т. е. разности аппликат точек А и В :
| В
1
В
0
| = |ВВ
//
| = | z
В
— z
A
| = ∆z
.
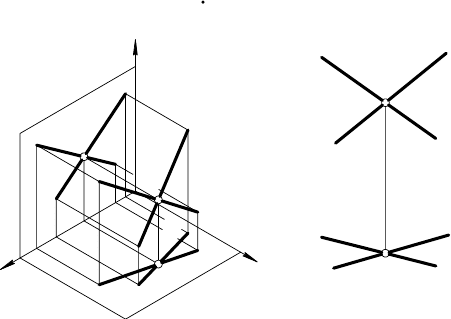
Для определения на эпюре угла наклона отрезка прямой
общего положения к плоскости π
3
строят прямоугольный тре-
угольник, одним из катетов которого является проекция отрезка
на плоскость π
3
, а вторым ∆x концов отрезка (рис. 38).
Рассмотренный способ построения натуральной величины
отрезка называют способом прямоугольного треугольника
(рис. 38).
D
z
a Å
A
2
B
2
B
3
A
3
A
0
x
y
z
y
Î
B
1
A
1
B
0
D
z
D
y
B
0
D
y
|
A B
|
b Å
|
A B
|
|
A B
|
D
x
D
x
B
|
1
g Å
Рис. 38

40
Для графического определения на эпюре Монжа натуральной ве-
личины отрезка прямой общего положения и углов его наклона к
плоскостям проекций π
1
, π
2
и π
3
, строят прямоугольный тре-
угольник по двум катетам, за один из которых выбирают гори-
зонтальную, фронтальную или профильную проекцию, а за другой
катет — соответственно разность аппликат (∆z), ординат (∆y)
или абсцисс (∆x) концов отрезка. Гипотенуза треугольника равна
натуральной величине отрезка, а угол между гипотенузой и про-
екцией отрезка на плоскость π
1
, π
2
или π
3
равен углу наклона
этого отрезка к плоскости π
1
, π
2
или π
3
.
41
Лекция 3 (2 часа)
Тема «Прямая и плоскость»
План
1. Взаимное расположение прямых.
2. Теорема об ортогональных проекциях прямого угла.
3. Способы задания плоскости.
4. Принадлежность прямой и точки плоскости.
5. Плоскости общего и частного положения.
6. Главные линии плоскости.
7. Угол наклона плоскости к плоскости проекции.
3.1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
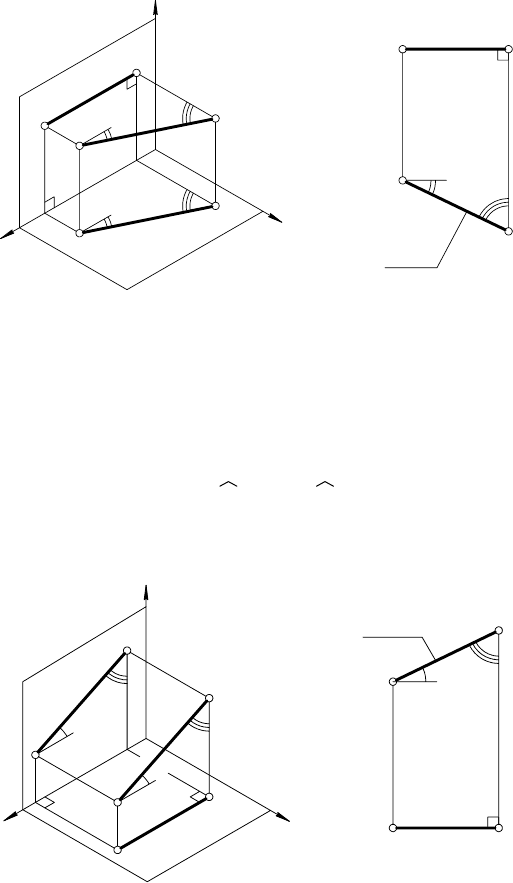
Взаимодействие двух прямых определяется наличием или
отсутствием у этих прямых общей точки:
— если прямые а и b имеют действительную общую точку,
то a I b = К ;
— если прямые а и b имеют несобственную общую точку, то
a I b = К
∞
и а || b ;
— если же прямые не имеют общих точек, то это скрещи-
вающиеся прямые a – b (см. 1.3., табл. 5).
p
2
p
1
z
y
x
a
2
Î
b
2
K
2
a
1
b
1
a
K
1
b
K
K
2
K
1
a
2
b
1
b
2
a
1
а б
Рис. 39
