Мота А.Н. Конспект лекций по начертательной геометрии

122

проекция совпадает с α

2

. С помощью вертикальной линии

связи, определяют 1

2

∈

α

2

. Высших точек две — 14 и 15. Они

принадлежат высшей параллели поверхности вращения и

находятся без дополнительных построений. Точка А (А

1

, А

2

)

— граница видимости фронтальной проекции сечения, лежит

на главном меридиане (в плоскости λ). Граничные точки ви-

димости горизонтальной проекции сечения (8 и 9 ) располо-

жены на экваторе.

2.

Для построения промежуточных точек — 2, 3, 4, 5, 6, 7, … , 13

используют ряд вспомогательных горизонтальных секущих

плоскостей γ, γ

1

… , γ

6

, которые пересекают искомую поверх-

ность вращения по параллелям, проецирующимся на π

1

в

окружности. Горизонтальные проекции промежуточных то-

чек 2

1

, 3

1

, 4

1

, 5

1

… 13

1

определяют на пересечении δ

1

с соот-

ветствующей параллелью. По вертикальным линиям связи

на плоскостях γ, γ

1

… , γ

6

находят фронтальные проекции то-

чек 2

2

, 3

2

, 4

2

, 5

2

… 13

2

.

3.

Горизонтальная проекция сечения l

1

принадлежит δ

1

, а фрон-

тальная l

2

представляет собой кривую линию, которую полу-

чают, соединяя между собой фронтальные проекции постро-

енных точек. Сечение l поверхности Ф (g, i

) плоскостью δ

определено на эпюре двумя своими проекциями:

l

(l

1

, l

2

) = Ф (g, i

) I δ

.

Построение сечения конической поверхности вращения

Поверхность прямого кругового конуса занимает особое ме-

сто среди других поверхностей вращения, так как она служит

носителем кривых второго порядка: эллипса, окружности, пара-

болы и гиперболы. Покажем, что все эти кривые могут быть

получены в результате сечения конуса вращения плоскостью

того или иного положения (отчего эти кривые и получили на-

звание

конических сечений).

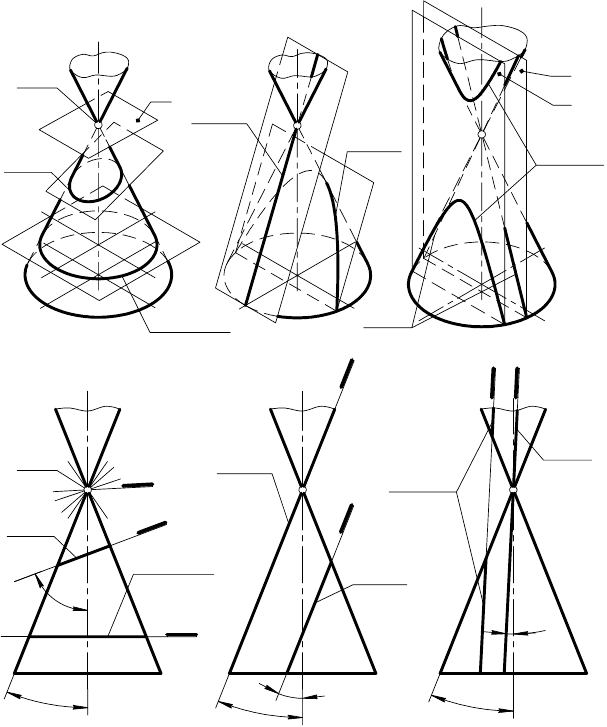
На рис. 131, а показаны положения секущей плоскости для

получения эллипса (плоскость α

2

), окружности (плоскость α

1

) и

одна из плоскостей (принадлежащих связке плоскостей), прохо-

дящих через вершину конической поверхности и пересекающих

эти поверхности по двум мнимым прямым, пересекающимся в

действительной точке (плоскость α

3

). На рис. 131, б показаны

положения секущей плоскости для получения параболы (плос-

кость β

1

) и плоскость β

2

, имеющая с конической поверхностью

123

общую прямую (две совпавшие прямые). На рис. 131, в изобра-

жена плоскость γ

1

, пересекающая конус по гиперболе, и плос-

кость γ

2

, в сечении которой образуются две пересекающиеся пря-

мые.

b

1

b

2

f

Å

y

Å

Ý ë ë è ï ñ

Ò î ÷ ê à

Î ê ð ó æ í î ñ ò ü

Ä â î é í à ÿ

ï ð ÿ ì à ÿ

b

1

2

b

2

a

1

2

a

2

a

3

2

Ò î ÷ ê à

Ý ë ë è ï ñ

Î ê ð ó æ í î ñ ò ü

Ä â î é í à ÿ

ï ð ÿ ì à ÿ

Ï ð à á î ë à

a

1

a

2

f

Å

y

Å

f

Å

y

Å

Ã è ï å ð á î ë à

Ä â å

ï ð ÿ ì û å

g

2

g

1

2

y Å

<

f Å

y Å

=

f Å

y Å

>

f Å

Ã è ï å ð á î ë à

a

3

g

1

g

2

Ä â å

ï ð ÿ ì û å

а б в

г д е

Рис. 131

На рис. 131, г, д, е приведены фронтальные проекции по-

верхности прямого кругового конуса, следы фронтально про-

ецирующих секущих плоскостей и указан вид получаемой в се-

чении кривой. Этот рисунок демонстрирует признаки, обеспе-

124

чивающие получение в сечении той или иной кривой второго

порядка. Так, если обозначить угол наклона образующей кони-

ческой поверхности к его оси через ϕ°, а угол между секущей

плоскостью и той же осью через ψ°, то можно утверждать, что

при ψ°

> ϕ° (рис. 131, г) в сечении получается эллипс (в частном

случае, если ψ° = 90° — окружность), при ψ°

= ϕ° (рис. 131, д) —

парабола и при ψ°

< ϕ° (рис. 131, е) — гипербола.

Если секущая плоскость занимает общее положение по от-

ношению к плоскостям проекций, то целесообразно с помощью

способов преобразования привести ее в проецирующее положе-

ние и свести решение задачи к одному из случаев, рассмотрен-

ных ранее (см. рис. 131, г, д, е).

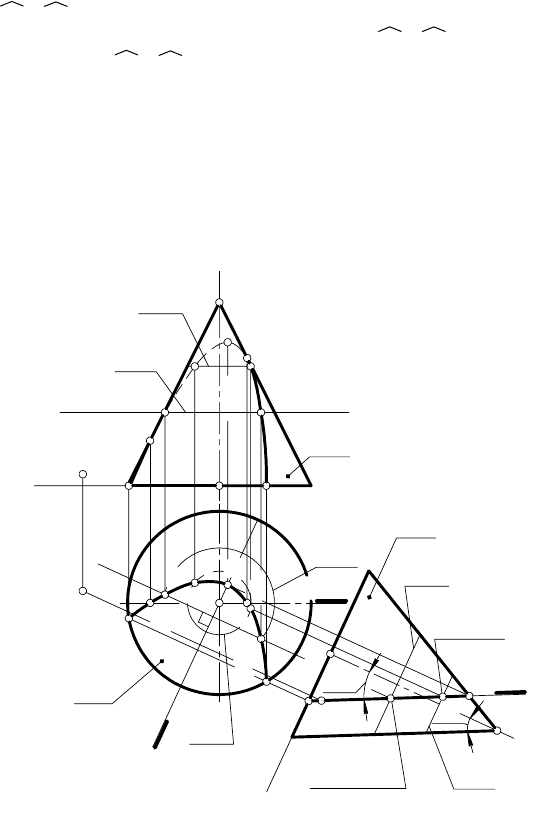
ЗАДАЧА. Построить проекции сечения конуса вращения

δ плоскостью общего положения α (h, K ) (рис. 132).

p

2

p

1

x

A

2

S

2

E

2

4

2

1

2

3

2

h

2

h

1

2

d

2

h

2

K

2

B

2

D

2

C

2

g

1

≡

h

0

g

h

1

h

2

1

d

1

h

1

B

1

C

1

2

1

D

1

3

1

A

1

E

1

4

1

O

1

≡

S

1

b

2

p

3

x

1

p

1

B

3

≡

C

3

K

1

K

3

h

1

≡

1

3

≡

2

3

≡

4

3

A

3

a

3

S

3

h

2

3

h

1

3

O

3

O

2

d

3

y Å

j Å

Рис. 132

125

РЕШЕНИЕ.

1.

Чтобы определить кривую в сечении конуса, выполняют

замену плоскости π

2

на π

3

, так чтобы плоскость π

3

была

перпендикулярна к плоскости α ( h, K ):

1

2

π

x

→

1

3

1

π

x

;

π

3

⊥ h ∈ α, x

1

⊥ h

1

, и строят α

3

и δ

3

.

2.

Сравнивают величины углов ψ° и ϕ° и определяют по какой

кривой второго порядка плоскость α (h, K) пересекает δ. Так

как ψ° = ϕ°, то в сечении будет парабола (рис. 131, д).

3.

Строят горизонтальную проекцию параболы, определив про-

екции A

1

, B

1

, C

1

, D

1

, E

1

и 1

1

, 2

1

, 3

1

и 4

1

точек A, B, C, D, E и

1, 2, 3 и 4. Высшая точка A лежит в плоскости β, проходя-

щей через ось вращения конуса и перпендикулярной гори-

зонтали h ⊂ α. Низшие точки B и C расположены на осно-

вании конуса. Точки D и E, являющиеся граничными точ-

ками видимости

для фронтальной проекции, определяются с

помощью главной меридиональной плоскости конуса γ

(γ

1

≡ h

0

γ

).

4.

Строят фронтальную проекцию параболы, определив проек-

ции A

2

, B

2

, C

2

, D

2

, E

2

и 1

2

, 2

2

, 3

2

и 4

2

. Проекции промежуточ-

ных точек 1, 2, 3 и 4 определяют с помощью проведения па-

раллелей h

1

и h

2

.

При сечении сферы плоскостью получается окружность, ор-

тогональные проекции которой строятся аналогично проекциям

окружностей, рассмотренных в 8.3.

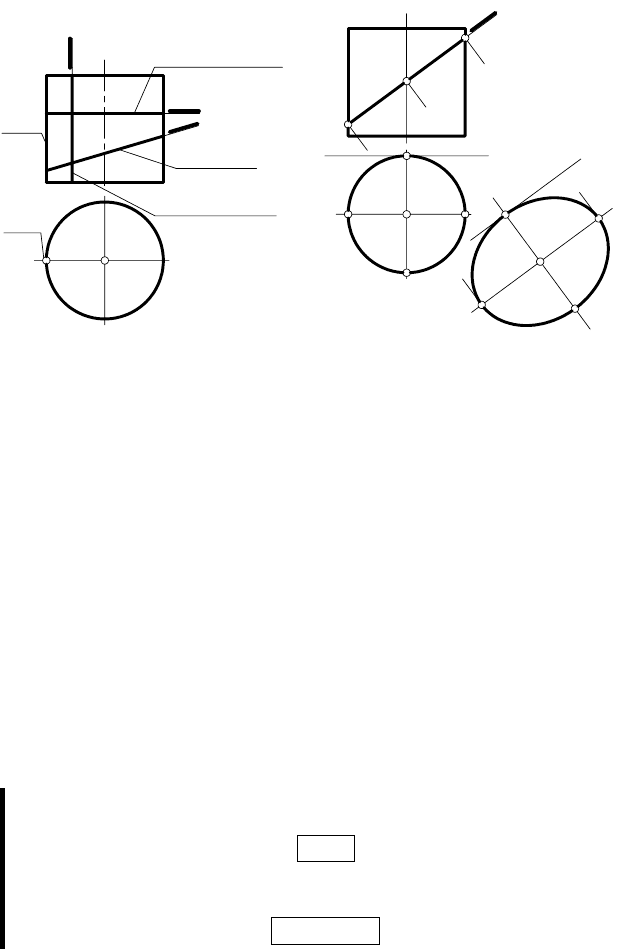
Цилиндр вращения может пересекаться плоскостью по ок-

ружности, эллипсу или двум образующим (рис. 133).

На рис. 134 показано построение сечения цилиндра враще-

ния фронтально проецирующей плоскостью β. Линией пересе-

чения является эллипс, большой осью которого служит

отре-

зок [AB ], а малой — отрезок [CD ]. Натуральный вид эллипса

определен с помощью замены плоскости π

1

на π

3

|| β.

Построение линии пересечения цилиндра вращения плоско-

стью общего положения сводится к случаям, рассмотренным на

рис. 133, с помощью одного из способов преобразования черте-

жа, обращающего секущую плоскость в плоскость частного по-

ложения.

126

g

1

g

2

a

1

2

a

2

a

3

2

i

2

i

1

ý ë ë è ï ñ

î ê ð ó æ í î ñ ò ü

ä â å ï ð ÿ ì û å

B

2

O

1

A

1

C

1

B

1

D

1

b

2

A

2

O

2

x

p

2

p

1

p

2

p

3

x

1

C

3

A

3

D

3

B

3

Рис. 133 Рис. 134

10.5. АЛГОРИТМ ПОСТРОЕНИЯ ТОЧКИ ПЕРЕСЕЧЕНИЯ

ПРЯМОЙ С ПОВЕРХНОСТЬЮ (a I Ф)

Рассмотрим общий случай решения задачи по определению

точек пересечения (встречи) линии с поверхностью. Частные

случаи этой задачи были рассмотрены ранее:

1)

пересечение прямой с плоскостью (см. 4.4.);

2)

пересечение прямой с поверхностью многогранника

(см. 5.3.).

Если заданы произвольные прямая и поверхность, то для

определения точек их пересечения необходимо выполнить сле-

дующие построения: заключить данную прямую во вспомога-

тельную плоскость; определить линию пересечения вспомога-

тельной плоскости с заданной поверхностью; отметить точки

пересечения данной прямой с линией пересечения плоскости и

поверхности.

Приведенные построения могут быть записаны в

виде алгоритма:

1. Заключить данную прямую во вспомогательную плоскость:

l ⊂ γ

2. Определить линию пересечения вспомогательной плоскости с

заданной поверхностью:

γ

I α

= m

127

3. Найти точки пересечения заданной прямой с линией пересече-

ния поверхности со вспомогательной плоскостью:

M

1

, M

2

, = l I m

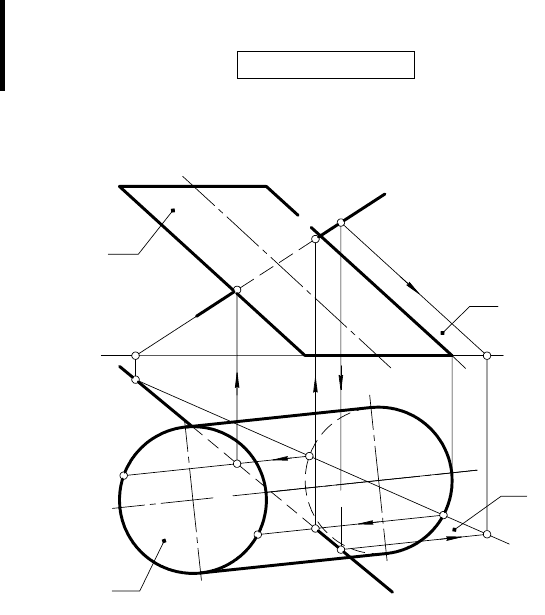
ЗАДАЧА. Построить точки встречи прямой l с поверхно-

стью эллиптического цилиндра α с круговым основанием

(рис. 135).

a

2

K

1

2

1

2

1

K

2

g

1

l

1

K

1

2

1

3

1

K

2

1

g

1

g

2

H

a

≡

H

a

1

x

l

2

h

0

g

a

1

H

a

2

a

2

g

2

H

l

≡

H

l

1

H

l

2

a

1

2

/

1

3

/

1

Рис. 135

РЕШЕНИЕ.

1. Чтобы получить рациональное решение прямую l заключают

в плоскость γ общего положения, параллельную образующей

цилиндра g. Тогда плоскость γ пересечет боковую поверх-

ность цилиндра по двум прямым — его образующим. Для

этого на прямой l берут произвольную точку 1 и через нее

проводят прямую a || g.

2. Определяют линию пересечения плоскости

γ и цилиндра α:

γ I α = 22

/

∧ 33

/

. Для этого находят горизонтальные следы

на H

a

и H

l

прямых a и l и проводят горизонтальный след h

0

γ

плоскости γ. Этот след, как и нижнее основание цилиндра α,

расположен в плоскости π

1

и пересекает окружность основа-

ния в точках 2 и 3 (на рис. 135 показаны только горизон-

128

тальные проекции 2

1

и 3

1

этих точек). Через точки 2

1

и 3

1

проводят горизонтальные проекции

/

11

22

и

/

11

33

образую-

щих цилиндра 22

/

и 33

/

, по которым его пересекает плос-

кость γ.

3. Отмечают точки

1

K

и

2

1

K

пересечения проекций образую-

щих

/

11

22

и

/

11

33

с горизонтальной проекцией l

1

прямой l.

Фронтальные проекции

1

2

K

и

2

K

искомых точек пересече-

ния определяют на l

2

с помощью линий связи.

129

Лекция 11 (2 часа)

Тема «Построение линии пересечение поверхностей

(Ф

I

Ф

1

)»

План

1.

Способ вспомогательных секущих плоскостей.

2.

Способ концентрических сфер.

В общем случае линией взаимного пересечения поверхно-

стей является пространственная кривая линия, которая может

распадаться на отдельные части, в том числе и плоские

(см. 10.4.).

Порядок построения линии взаимного пересечения поверх-

ностей аналогичен порядку построения линии пересечения по-

верхности плоскостью.

Для построения точек кривой пересечения поверхностей ис-

пользуют

алгоритм (см. 10.3.).

11.1. СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ

Рассмотрим случай, при котором в качестве секущих по-

верхностей γ

j

берут плоскости (см. 10.3., рис. 129). Тогда поль-

зуются не отдельными плоскостями, а пучком плоскостей, при-

чем ось пучка может быть как собственной, так и несобствен-

ной прямой.

Рассмотрим определение линии пересечения поверхностей с

помощью пучка плоскостей, ось которого несобственная пря-

мая. В этом случае плоскости пучка будут параллельны, и спо-

соб построения линии пересечения называют способом парал-

лельных секущих плоскостей. Использовать такой способ мож-

но тогда, когда секущие плоскости пересекают обе поверхности

по графически простым линиям (окружностям или

прямым).

Примером может служить построение линии пересечения

сферической и конической поверхностей.

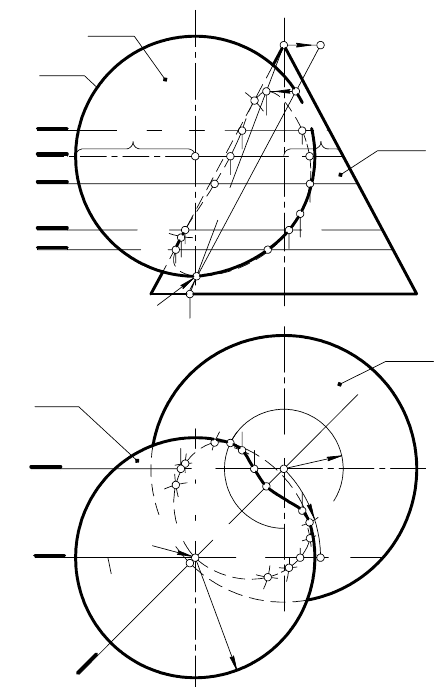
ЗАДАЧА. Построить линию взаимного пересечения по-

верхности сферы Ф с поверхностью конуса вращения Ф

1

(рис. 136).

130

S

2

S

1

2

i

2

Ô

2

Ô

1

2

A

2

A

1

2

3

2

4

2

b

5

2

b

3

2

b

1

2

b

2

b

4

2

O

2

R

r

D

2

C

2

5

2

6

2

7

2

8

2

1 1

2

1 2

2

r

A

1

9

2

1 0

2

1 0

1

9

1

4

1

C

1

S

1

3

1

D

1

6

1

5

1

8

1

7

1

1 2

1

1 1

1

i

1

≡

1

≡

B

1

≡

B

1

≡

O

1

≡

i

1

2

1

m

1

m

1

a

1

a

3

1

a

2

1

Ô

1

Ô

1

2

1

2

≡

1

2

≡

B

1

2

≡

B

2

m

1

2

F

1

F

2

R

S

1

Рис. 136

РЕШЕНИЕ.

В данном примере обе поверхности рассекаются горизон-

тальными плоскостями уровня β

1

, β

2

, β

3

, … по графически про-

стым линиям — окружностям.

Порядок построения:

1.

Находят экстремальные точки: A — самая высокая, B — самая

низкая. Эти точки расположены в плоскости α

1

, проходящей

через оси вращения поверхностей сферы и конуса, и явля-

ются точками пересечения меридиана сферы с образующей

131

конуса S2. Для построения точек A и B использован способ

вращения вокруг прямой i ⊥ π

1

(i — ось вращения сферы).

Меридиан сферы m, лежащий в плоскости α

1

, вращают во-

круг оси i до положения главного меридиана, и одновремен-

но с ним вращают вокруг той же оси образующую конуса S2

до положения, параллельного π

2

. Для этого достаточно по-

вернуть одну точку S образующей (S2 ), так как точка

1 = (S2 )

I

i лежит на оси вращения (1 ≡1

1

). При вращении

точки S вокруг i получают точку S

1

(

1

S

,

1

2

S

). Точки S

1

и 1 ≡

1

определяют положение образующей (S

1

2

1

). Совмещенный

с главным меридиан m

1

и образующая (S

1

2

1

) пересекаются в

точках A

1

и B

1

(фронтальные проекции

1

2

A и

1

2

B ). Обратным

вращением (S

1

2

1

) → (S2 ) находят фронтальные проекции A

2

и B

2

≡

1

2

B

≡1

2

≡

1

2

1

и горизонтальные проекции A

1

, B

1

≡

1

B

.

2.

Определяют границы видимости: точки, лежащие на очерке

одной из поверхностей, в данном случае на очерке сферы.

Точки, являющиеся границами видимости горизонталь-

ной проекции линии пересечения поверхностей, лежат на

одноименной проекции экватора сферы (точки C

1

и D

1

). Для

построения этих точек применяют алгоритм:

а) вводят секущую плоскость β

1

;

б) строят линии пересечения плоскости β

1

с поверхно-

стями сферы Ф (параллель радиуса R ) и конуса Ф

1

(параллель радиуса r );

в) определяют точки пересечения построенных линий

(точки C и D ).

Границы видимости фронтальной проекции линии пере-

сечения лежат на фронтальной проекции главного меридиа-

на сферы, так как сфера находится ближе к наблюдателю,

чем конус. На π

2

видна часть линии пересечения, располо-

женная в передней части сферы (перед плоскостью α

3

). Точ-

ки, являющиеся границей видимости, B

1

и F

1

лежат в плос-

кости α

3

. Точка B построена ранее, как самая низкая точка,

а точку F, в данной задаче, определяют после того, как со-

единят найденные ранее точки горизонтальной проекции

линии пересечения поверхностей.

3.

Определяют достаточное (для построения линии пересечения

поверхностей) количество промежуточных точек 3, 4, 5, 6, 7,

8, 9, 10, 11, 12. Точки строят, применяя алгоритм (см. по-

Мота А.Н. Конспект лекций по начертательной геометрии

Подождите немного. Документ загружается.