Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics
Подождите немного. Документ загружается.


Substituting values into the expression for T
2
T
2
5
10.79 lbmol2a4.96
Btu
lbmol ? 8R
b14608R21 10.21 lbmol2a4.99
Btu
lbmol ? 8R
b15408R2
10.79 lbmol2a4.96
Bt
u
lbmol ? 8R
b1 10.21 lbmol2a4.99
Btu
lbmol ? 8R
b
5 4778R
(b) The final mixture pressure p
2
can be determined using the ideal gas equation of state, p
2
5 nRT
2
/
V, where n
is the total number of moles of mixture and V is the total volume occupied by the mixture. The volume V is the
sum of the volumes of the two tanks, obtained with the ideal gas equation of state as follows
V 5
n
N
2
RT
N
2
p
N
2
1
n
O
2
RT
O
2
p
O
2
where p
N
2
5 2 atm is the initial pressure of the nitrogen and p
O
2
5
1
atm is the initial pressure of the oxygen.
Combining results and reducing
p
2
5
1n
N
2
1 n
O
2
2T
2
a
n
N
2
T
N
2
p
N
2
1
n
O
2
T
O
2
p
O
2
b
Substituting values
p
2
5
11.0 lbmol214778
R2
c
10.79 lbmol214608R
2
2 atm
1
10.21 lbmol215408R2
1 atm
d
5 1.62 atm
(c) Reducing the closed system form of the entropy balance
S
2
2 S
1
5
#
2
1
a
d
Q
T
b
b
0
1 s
where the entropy transfer term drops out for the adiabatic mixing process. The initial entropy of the system,
S
1
, is the sum of the entropies of the gases at the respective initial states
S
1
5 n
N
2
s
N
2
1T
N
2
, p
N
2
21 n
O
2
s
O
2
1T
O
2
, p
O
2
2
The final entropy of the system, S
2
, is the sum of the entropies of the individual components, each evaluated at
the final mixture temperature and the partial pressure of the component in the mixture
S
2
5 n
N
2
s
N
2
1T
2
, y
N
2
p
2
21 n
O
2
s
O
2
1T
2
, y
O
2
p
2
2
Collecting the last three equations
s 5 n
N
2
3s
N
2
1T
2
, y
N
2
p
2
22 s
N
2
1T
N
2
, p
N
2
24
1 n
O
2
3s
O
2
1T
2
, y
O
2
p
2
22 s
O
2
1T
O
2
, p
O
2
24
Evaluating the change in specific entropy of each gas in terms of a constant specific heat
c
p
, this becomes
s 5 n
N
2
ac
p, N
2
ln
T
2
T
N
2
2 R ln
y
N
2
p
2
p
N
2
b
1 n
O
2
ac
p, O
2
ln
T
2
T
O
2
2 R ln
y
O
2
p
2
p
O
2
b
The required values for
c
p
can be found by adding R to the c
y
values found previously (Eq. 3.45)
c
p, N
2
5 6.95
Bt
u
lbmol ? 8R
,
c
p, O
2
5 6.98
Bt
u
lbmol ? 8R
12.4 Analyzing Systems Involving Mixtures 723
c12IdealGasMixtureandPsychrometr723 Page 723 6/29/10 11:54:30 AM user-s146c12IdealGasMixtureandPsychrometr723 Page 723 6/29/10 11:54:30 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
724 Chapter 12 Ideal Gas Mixture and Psychrometric Applications
Determine the total volume of the final mixture, in ft
3
.
Ans. 215 ft
3
.
Since the total number of moles of mixture n 5 0.79 1 0.21 5 1.0, the mole fractions of the two gases are
y
N
2
5 0.79 and y
O
2
5 0.21.
Substituting values into the expression for s gives
s 5 0.79 lbmol c6.95
Bt
u
lbmol ? 8R
ln a
4778R
4608R
b2 1.986
Btu
lbmol ? 8R
ln a
10.79211.62 atm
2
2 atm
bd
1 0.21 lbmol c6.98
Bt
u
lbmol ? 8R
ln a
4778R
5408R
b21.986
Btu
lbmol ? 8R
ln a
10.21211.62 atm
2
1 atm
bd
➊ 5 1.168 Btu
/
8R
➊ Entropy is produced when different gases, initially at different temperatures and
pressures, are allowed to mix.
Ability to…
❑
analyze the adiabatic
mixing of two ideal gases
at constant total volume.
❑
apply energy and entropy
balances to the mixing of
two gases.
❑
apply ideal gas mixture
principles assuming con-
stant specific heats.
✓
Skills Developed
In the next example, we consider a control volume at steady state where two incoming
streams form a mixture. A single stream exits.
c c c c EXAMPLE 12.6 c
At steady state, 100 m
3
/min of dry air at 32°C and 1 bar is mixed adiabatically with a stream of oxygen (O
2
) at
127°C and 1 bar to form a mixed stream at 478C and 1 bar. Kinetic and potential energy effects can be ignored.
Determine (a) the mass flow rates of the dry air and oxygen, in kg/min, (b) the mole fractions of the dry air and
oxygen in the exiting mixture, and (c) the time rate of entropy production, in kJ/K ? min.
SOLUTION
Known:
At steady state, 100 m
3
/min of dry air at 328C and 1 bar is mixed adiabatically with an oxygen stream
at 1278C and 1 bar to form a mixed stream at 478C and 1 bar.
Find: Determine the mass flow rates of the dry air and oxygen, in kg/min, the mole fractions of the dry air and
oxygen in the exiting mixture, and the time rate of entropy production, in kJ/K ? min.
Schematic and Given Data:
Analyzing Adiabatic Mixing of Two Streams
3
Mixed stream
Insulation
1
2
T
3
= 47°C
p
3
= 1 bar
T
2
= 127°C
p
2
= 1 bar
T
1
p
1
(AV)
1
= 32°C
= 1 bar
= 100 m
3
/min
Air
Oxygen
Fig. E12.6
Engineering Model:
1.
The control volume identified by the dashed line on the accompanying figure operates at steady state.
2. No heat transfer occurs with the surroundings.
c12IdealGasMixtureandPsychrometr724 Page 724 7/29/10 4:51:59 PM user-s146c12IdealGasMixtureandPsychrometr724 Page 724 7/29/10 4:51:59 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

3. Kinetic and potential energy effects can be ignored, and W
#
cv
5 0.
4. The entering gases can be regarded as ideal gases. The exiting mixture can be regarded as an ideal gas
mixture adhering to the Dalton model.
5. The dry air is treated as a pure component.
Analysis:
(a)
The mass flow rate of the dry air entering the control volume can be determined from the given volumetric
flow rate (AV)
1
m
a1
#
5
1AV2
1
y
a1
where y
a
1
is the specific volume of the air at 1. Using the ideal gas equation of state
y
a1
5
1
R
/
M
a
2T
1
p
1
5
a
8314
28.97
N ? m
kg ? K
b1305 K2
10
5
N
/
m
2
5 0.875
m
3
kg
The mass flow rate of the dry air is then
m
#
a1
5
100 m
3
/
min
0.875 m
3
/
kg
5 114.29
kg
min
The mass flow rate of the oxygen can be determined using mass and energy rate balances. At steady state,
the amounts of dry air and oxygen contained within the control volume do not vary. Thus, for each component
individually it is necessary for the incoming and outgoing mass flow rates to be equal. That is
m
#
a1
5 m
#
a3
1dry air2
m
#
o2
5 m
#
o3
1oxygen2
Using assumptions 1–3 together with the foregoing mass flow rate relations, the energy rate balance reduces to
0 5 m
#
a
h
a
1T
1
21 m
#
o
h
o
1T
2
22 3m
#
a
h
a
1T
3
21 m
#
o
h
o
1T
3
24
where m
#
a
and m
#
o
denote the mass flow rates of the dry air and oxygen, respectively. The enthalpy of the mixture
at the exit is evaluated by summing the contributions of the air and oxygen, each at the mixture temperature.
Solving for m
#
o
m
#
o
5 m
#
a
c
h
a
1T
3
22 h
a
1T
1
2
h
o
1T
2
22 h
o
1T
3
2
d
The specific enthalpies can be obtained from Tables A-22 and A-23. Since Table A-23 gives enthalpy values
on a molar basis, the molecular weight of oxygen is introduced into the denominator to convert the molar
enthalpy values to a mass basis
m
#
o
5
1114.29 kg
/
min21320.29 kJ
/
kg 2 305.22 kJ
/
kg2
a
1
32 kg
/
kmol
b111,711 kJ
/
kmol 2 9,325 kJ
/
kmol2
5 23.1
kg
min
(b) To obtain the mole fractions of the dry air and oxygen in the exiting mixture, first convert the mass flow
rates to molar flow rates using the respective molecular weights
n
#
a
5
m
#
a
M
a
5
114.29 kg
/
min
28.97 k
g
/
kmol
5 3.95 kmol
/
min
n
#
o
5
m
#
o
M
o
5
23.1
kg
/
min
32 kg
/
kmol
5 0.72 kmol
/
min
12.4 Analyzing Systems Involving Mixtures 725
c12IdealGasMixtureandPsychrometr725 Page 725 6/29/10 11:54:38 AM user-s146c12IdealGasMixtureandPsychrometr725 Page 725 6/29/10 11:54:38 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

726 Chapter 12 Ideal Gas Mixture and Psychrometric Applications
What are the mass fractions of air and oxygen in the exiting
mixture? Ans. mf
air
5 0.832, mf
O2
5 0.168.
where n
#
denotes molar flow rate. The molar flow rate of the mixture
n
#
is the sum
n
#
5 n
#
a
1 n
#
o
5 3.95 1 0.72 5 4.67 kmol
/
min
The mole fractions of the air and oxygen in the exiting mixture are, respectively
➊ y
a
5
n
#
a
n
#
5
3.9
5
4.67
5 0.846
and
y
o
5
n
#
o
n
#
5
0.7
2
4.67
5 0.154
(c) For the control volume at steady state, the entropy rate balance reduces to
0 5 m
#
a
s
a
1T
1
,p
1
21 m
#
o
s
o
1T
2
, p
2
22 3m
#
a
s
a
1T
3
, y
a
p
3
21 m
#
o
s
o
1T
3
, y
o
p
3
241 s
#
The specific entropy of each component in the exiting ideal gas mixture is evaluated at its partial pressure in
the mixture and at the mixture temperature. Solving for s
#
s
#
5 m
#
a
3s
a
1T
3
, y
a
p
3
22 s
a
1T
1
, p
1
241 m
#
o
3s
o
1T
3
, y
o
p
3
22 s
o
1T
2
, p
2
24
Since p
1
5 p
3
, the specific entropy change of the dry air is
s
a
1T
3
, y
a
p
3
22 s
a
1T
1
, p
1
25 s8
a
1T
3
22s8
a
1T
1
22
R
M
a
ln
y
a
p
3
p
1
5 s8
a
1T
3
22 s8
a
1T
1
22
R
M
a
ln y
a
The s8
a
terms are evaluated from Table A-22. Similarly, since p
2
5 p
3
, the specific entropy change of the oxygen is
s
o
1T
3
, y
o
p
3
22 s
o
1T
2
, p
2
25
1
M
o
3s8
o
1T
3
22 s8
o
1T
2
22 R ln y
o
4
The s8
o
terms are evaluated from Table A-23. Note the use of the molecular weights M
a
and M
o
in the last two
equations to obtain the respective entropy changes on a mass basis.
The expression for the rate of entropy production becomes
s
#
5 m
#
a
cs8
a
1T
3
22 s8
a
1T
1
22
R
M
a
ln y
a
d1
m
#
o
M
o
3s8
o
1T
3
22 s8
o
1T
2
22 R ln y
o
4
Substituting values
s
#
5 a114.29
k
g
min
bc1.7669
k
J
kg ? K
21.71865
kJ
kg ? K
2 a
8.314
28.97
kJ
kg ? K
b ln 0.846 d
1 a
23.1 kg
/
min
32 kg
/
kmol
bc207.112
k
J
kmol ? K
2 213.765
kJ
kmol ? K
2 a8.314
kJ
kmol ? K
b ln 0.154 d
➋ 5 17.42
k
J
K ? min
➊ This calculation is based on dry air modeled as a pure component (assump-
tion 5). However, since O
2
is a component of dry air (Table 12.1), the actual
mole fraction of O
2
in the exiting mixture is greater than given here.
➋ Entropy is produced when different gases, initially at different temperatures,
are allowed to mix.
Ability to…
❑
analyze the adiabatic mixing
of two ideal gas streams at
steady state.
❑
apply ideal mixture principles
together with mass, energy,
and entropy rate balances.
✓
Skills Developed
c12IdealGasMixtureandPsychrometr726 Page 726 6/29/10 11:54:41 AM user-s146c12IdealGasMixtureandPsychrometr726 Page 726 6/29/10 11:54:41 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

Psychrometric Applications
The remainder of this chapter is concerned with the study of systems involving mix-
tures of dry air and water vapor. A condensed water phase also may be present.
Knowledge of the behavior of such systems is essential for the analysis and design
of air-conditioning devices, cooling towers, and industrial processes requiring close
control of the vapor content in air. The study of systems involving dry air and water
is known as psychrometrics.
BIOCONNECTIONS Does spending time inside a building cause you to
sneeze, cough, or develop a headache? If so, the culprit could be the ambient air.
The term sick building syndrome (SBS) describes a condition where indoor air qual-
ity leads to acute health problems and comfort issues for building occupants. Effects of
SBS are often linked to the amount of time an occupant spends within the space; yet while
the specific cause and illness are frequently unidentifiable, symptoms typically subside
after the occupant leaves the building. If the symptoms persist even after leaving the space
and are diagnosed as a specific illness attributed to an airborne contaminant, the term
building-related illness is a more accurate descriptor.
The U.S. Environmental Protection Agency (EPA) recently conducted a study of 100
domestic office buildings, the largest study of its kind. The results agree with most previous
findings that relate lower ventilation rates per person within office buildings to higher rates
of SBS symptom reporting. Building codes and guidelines in the U.S. generally recommend
ventilation rates within office buildings in the range of 15–20 ft
3
/min per occupant. Some
of the spaces studied had ventilation rates below the guidelines.
Careful design is needed to ensure that air distribution systems deliver acceptable ventila-
tion for each space. Inadequate system installation and improper maintenance also can give
rise to indoor air quality problems, even when appropriate standards have been applied in the
design. The EPA study found this to be the case with the systems of many buildings in the
study group. Also, testing and balancing of the installed systems were never conducted in
several of the buildings to ensure that systems were operating according to design intent.
Indoor air quality continues to be a significant concern for both building occupants and
engineers who design and operate building air delivery systems.
psychrometrics
moist air
12.5 Introducing Psychrometric Principles
The object of the present section is to introduce some important definitions and
principles used in the study of systems involving dry air and water.
12.5.1
Moist Air
The term moist air refers to a mixture of dry air and water vapor in which the dry air
is treated as if it were a pure component. As can be verified by reference to appropri-
ate property data, the overall mixture and each mixture component behave as ideal
gases at the states under present consideration. Accordingly, for the applications to be
considered, the ideal gas mixture concepts introduced previously apply directly.
In particular, the Dalton model and the relations provided in Table 12.2 are appli-
cable to moist air mixtures. Simply by identifying gas 1 with dry air, denoted by the
subscript a, and gas 2 with water vapor, denoted by the subscript v, the table gives a
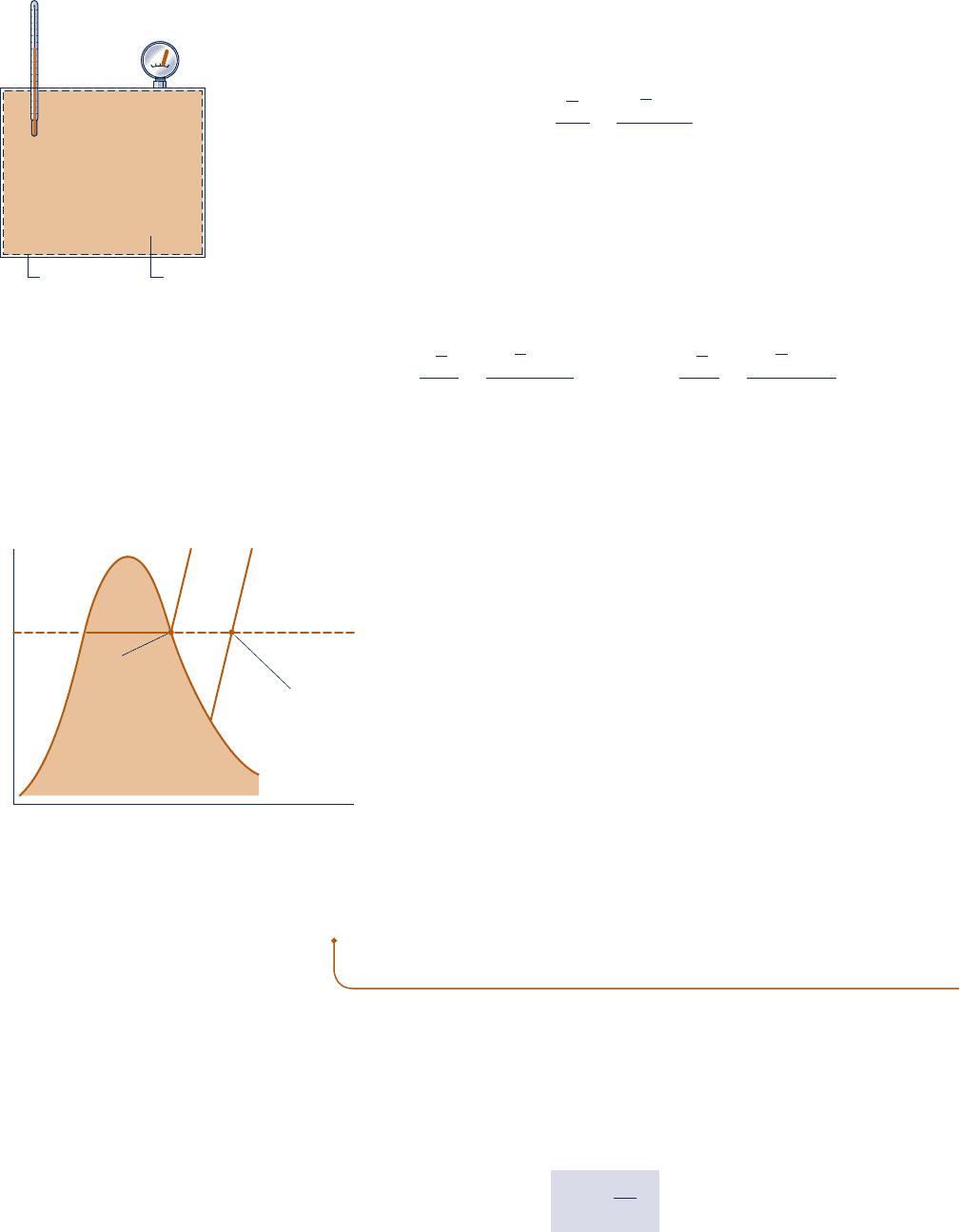
useful set of moist air property relations. Referring to Fig. 12.3, let’s verify this point by
obtaining a sampling of moist air relations and relating them to entries in Table 12.2.
TAKE NOTE...
Moist air is a binary mixture
of dry air and water vapor,
and the property relations
of Table 12.2 apply.
12.5 Introducing Psychrometric Principles 727
c12IdealGasMixtureandPsychrometr727 Page 727 6/29/10 11:54:46 AM user-s146c12IdealGasMixtureandPsychrometr727 Page 727 6/29/10 11:54:46 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
728 Chapter 12
Ideal Gas Mixture and Psychrometric Applications
Shown in Fig. 12.3—a special case of Fig. 12.1—is a closed system consisting
of moist air occupying a volume V at mixture pressure p and mixture tem-
perature T. The overall mixture is assumed to obey the ideal gas equation of
state. Thus
p 5
nRT
V
5
m1
R
/
M2
T
V
(12.40)
where n, m, and M denote the moles, mass, and molecular weight of the mixture,
respectively, and n 5 m/M.
Each mixture component is considered to act as if it existed alone in the
volume V at the mixture temperature T while exerting a part of the pressure. The
mixture pressure is the sum of the partial pressures of the dry air and the water
vapor: p 5 p
a
1 p
v
. That is, the Dalton model applies.
Using the ideal gas equation of state, the partial pressures p
a
and p
v
of the
dry air and water vapor are, respectively
p
a
5
n
a
RT
V
5
m
a
1R
/
M
a
2T
V
,
p
v
5
n
v
RT
V
5
m
v
1R
/
M
v
2
T
V
(12.41a)
where n
a
and n
v
denote the moles of dry air and water vapor, respectively; m
a
, m
v
, M
a
,
and M
v
are the respective masses and molecular weights. The amount of water vapor
present is normally much less than the amount of dry air. Accordingly, the values of
n
v
, m
v
, and p
v
are small relative to the corresponding values of n
a
, m
a
, and p
a
.
Forming ratios with Eqs. 12.40 and 12.41a, we get the following
alternative expressions for p
a
and p
v
p
a
5 y
a
p,
p
v
5 y
v
p (12.41b)
where y
a
and y
v
are the mole fractions of the dry air and water
vapor, respectively. These moist air expressions conform to Eqs. (c)
in Table 12.2.
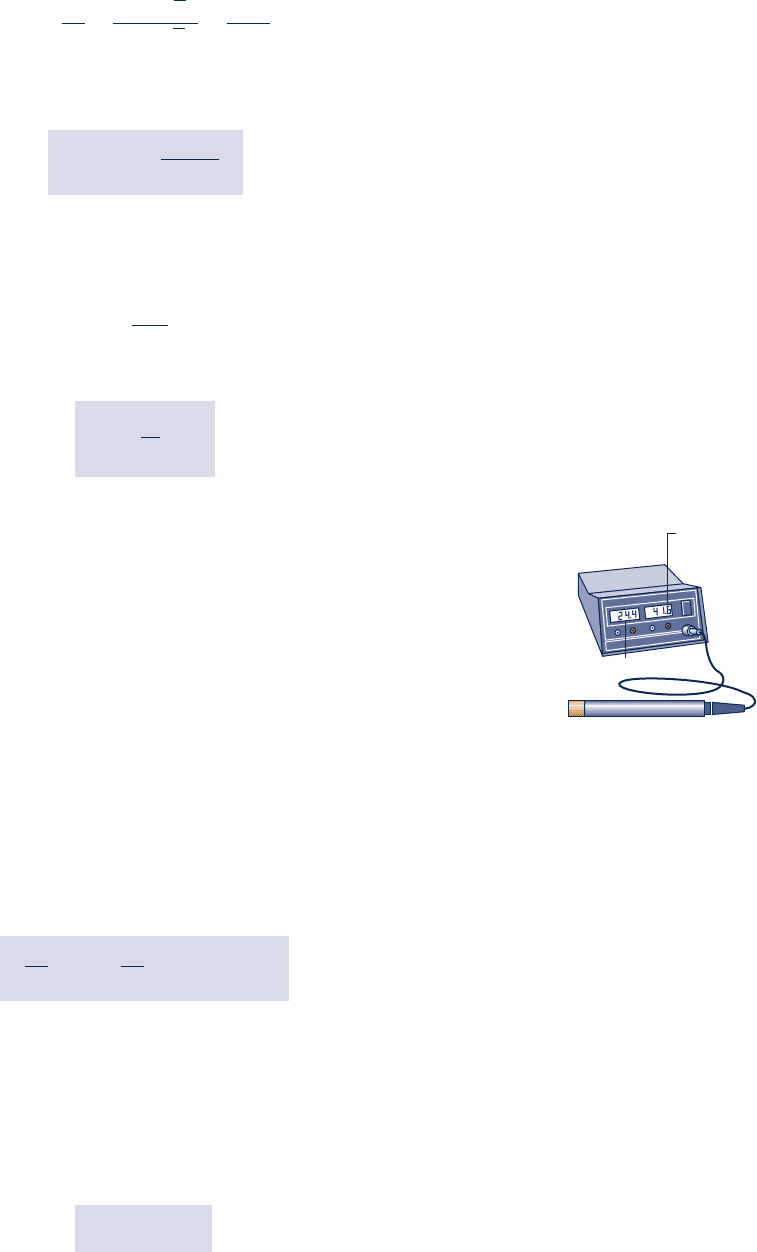
A typical state of water vapor in moist air is shown in Fig. 12.4.
At this state, fixed by the partial pressure p
v
and the mixture tem-
perature T, the vapor is superheated. When the partial pressure of
the water vapor corresponds to the saturation pressure of water at
the mixture temperature, p
g
of Fig. 12.4, the mixture is said to be
saturated. Saturated air is a mixture of dry air and saturated water
vapor. The amount of water vapor in moist air varies from zero in
dry air to a maximum, depending on the pressure and temperature,
when the mixture is saturated.
12.5.2
Humidity Ratio, Relative Humidity,
Mixture Enthalpy, and Mixture Entropy
A given moist air sample can be described in a number of ways. The mixture can be
described in terms of the moles of dry air and water vapor present or in terms of the
respective mole fractions. Alternatively, the mass of dry air and water vapor, or the
respective mass fractions, can be specified. The composition also can be indicated by
means of the humidity ratio v, defined as the ratio of the mass of the water vapor to
the mass of dry air
v
5
m
v
m
a
(12.42)
The humidity ratio is sometimes referred to as the specific humidity.
Fig. 12.3
Mixture of dry air and
water vapor.
Pressure = p
Temperature = T
Volume = VBoundary
dry air
water vapor
mixture
n
a
, m
a
:
n
v
, m
v
:
n, m:
saturated air
humidity ratio
T
v
p
g
p
v
Mixture
temperature
Typical state of the
water vapor in moist air
State of the
water vapor in a
saturated mixture
Fig. 12.4 T–y diagram for water vapor in an
air–water mixture.
c12IdealGasMixtureandPsychrometr728 Page 728 6/29/10 11:54:46 AM user-s146c12IdealGasMixtureandPsychrometr728 Page 728 6/29/10 11:54:46 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
The humidity ratio can be expressed in terms of partial pressures and molecular
weights by solving Eqs. 12.41a for m
a
and m
v
, respectively, and substituting the resulting
expressions into Eq. 12.42 to obtain
v 5
m
v
m
a
5
M
v
p
v
V
/
R
T
M
a
p
a
V
/
RT
5
M
v
p
v
M
a
p
a
Introducing p
a
5 p 2 p
v
and noting that the ratio of the molecular weight of water
to that of dry air, M
v
/M
a
, is approximately 0.622, this expression can be written as
v 5 0.622
p
v
p 2 p
v
(12.43)
Moist air also can be described in terms of the relative humidity f, defined as the ratio
of the mole fraction of water vapor y
v
in a given moist air sample to the mole fraction
y
v, sat
in a saturated moist air sample at the same mixture temperature and pressure:
f 5
y
v
y
v,sat
b
T, p
Since p
v
5 y
v
p and p
g
5 y
v,sat
p, the relative humidity can be expressed as
f 5
p
v
p
g
b
T, p
(12.44)
The pressures in this expression for the relative humidity are labeled on Fig. 12.4.
The humidity ratio and relative humidity can be measured. For laboratory measure-
ments of humidity ratio, a hygrometer can be used in which a moist air sample is exposed
to suitable chemicals until the moisture present is absorbed. The amount of water vapor
is determined by weighing the chemicals. Continuous recording of the relative humidity
can be accomplished by means of transducers consisting of resistance- or capacitance-
type sensors whose electrical characteristics change with relative humidity.
Evaluating H, U, and S for Moist Air
The values of H, U, and S for moist air modeled as an ideal gas mixture can be found
by adding the contribution of each component at the condition at which the component
exists in the mixture. For example, the enthalpy H of a given moist air sample is
H 5 H
a
1 H
v
5 m
a
h
a
1 m
v
h
v
(12.45)
This moist air expression conforms to Eq. (d) in Table 12.2.
Dividing by m
a
and introducing the humidity ratio gives the mixture enthalpy per
unit mass of dry air
H
m
a
5 h
a
1
m
v
m
a
h
v
5 h
a
1 vh
v
(12.46)
The enthalpies of the dry air and water vapor appearing in Eq. 12.46 are evaluated
at the mixture temperature. An approach similar to that for enthalpy also applies to
the evaluation of the internal energy of moist air.
Reference to steam table data or a Mollier diagram for water shows that the enthalpy
of superheated water vapor at low vapor pressures is very closely given by the saturated
vapor value corresponding to the given temperature. Hence, the enthalpy of the water
vapor h
v
in Eq. 12.46 can be taken as h
g
at the mixture temperature. That is
h
v
< h
g
1T2 (12.47)
relative humidity
mixture enthalpy
Temperature
Sensing element
Relative
humidity
12.5 Introducing Psychrometric Principles 729
c12IdealGasMixtureandPsychrometr729 Page 729 6/29/10 11:54:51 AM user-s146c12IdealGasMixtureandPsychrometr729 Page 729 6/29/10 11:54:51 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

730 Chapter 12
Ideal Gas Mixture and Psychrometric Applications
Equation 12.47 is used in the remainder of the chapter. Enthalpy data for water
vapor as an ideal gas from Table A-23 are not used for h
v
because the enthalpy datum
of the ideal gas tables differs from that of the steam tables. These different datums
can lead to error when studying systems that contain both water vapor and a liquid
or solid phase of water. The enthalpy of dry air, h
a
, can be obtained from the appro-
priate ideal gas table, Table A-22 or Table A-22E, however, because air is a gas at
all states under present consideration and is closely modeled as an ideal gas at these
states.
In accord with Eq. (h) in Table 12.2, the moist air mixture entropy has two contri-
butions: water vapor and dry air. The contribution of each component is determined
at the mixture temperature and the partial pressure of the component in the mixture.
Using Eq. 6.18 and referring to Fig. 12.4 for the states, the specific entropy of the
water vapor is given by s
v
(T, p
v
) 5 s
g
(T) 2 R ln p
v
/p
g
, where s
g
is the specific entropy
of saturated vapor at temperature T. Observe that the ratio of pressures, p
v
/p
g
, can
be replaced by the relative humidity f, giving an alternative expression.
Using Computer Software
Property functions for moist air are listed under the Properties menu of Interactive
Thermodynamics: IT. Functions are included for humidity ratio, relative humidity,
specific enthalpy and entropy as well as other psychrometric properties introduced
later. The methods used for evaluating these functions correspond to the methods
discussed in this chapter, and the values returned by the computer software agree
closely with those obtained by hand calculations with table data. The use of IT for
psychrometric evaluations is illustrated in examples later in the chapter.
mixture entropy
BIOCONNECTIONS Medical practitioners and their patients have long
noticed that influenza cases peak during winter. Speculation about the cause ranged
widely, including the possibility that people spend more time indoors in winter and
thus transmit the flu virus more easily, or that the peak might be related to less sunlight
exposure during winter, perhaps affecting human immune responses.
Since air is drier in winter, others suspected a link between relative humidity and influ-
enza virus survival and transmission. In a 2007 study, using influenza-infected guinea pigs
in climate-controlled habitats, researchers investigated the effects of variable habitat tem-
perature and humidity on the aerosol spread of influenza virus. The study showed there were
more infections when it was colder and drier, but relative humidity was a relatively weak
variable in explaining findings. This prompted researchers to look for a better rationale.
When data from the 2007 study were reanalyzed, a significant correlation was found
between humidity ratio and influenza. Unlike relative humidity, humidity ratio measures the
actual amount of moisture present in air. When humidity ratio is low, as in peak winter flu
months, the virus survives longer and transmission rates increase, researchers say. These
findings strongly point to the value of humidifying indoor air in winter, particularly in high-
risk places such as nursing homes.
12.5.3
Modeling Moist Air in Equilibrium with Liquid Water
Thus far, our study of psychrometrics has been conducted as an application of the
ideal gas mixture principles introduced in the first part of this chapter. However,
many systems of interest are composed of a mixture of dry air and water vapor in
contact with a liquid (or solid) water phase. To study these systems requires additional
considerations.
c12IdealGasMixtureandPsychrometr730 Page 730 6/30/10 8:09:54 PM user-s146c12IdealGasMixtureandPsychrometr730 Page 730 6/30/10 8:09:54 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
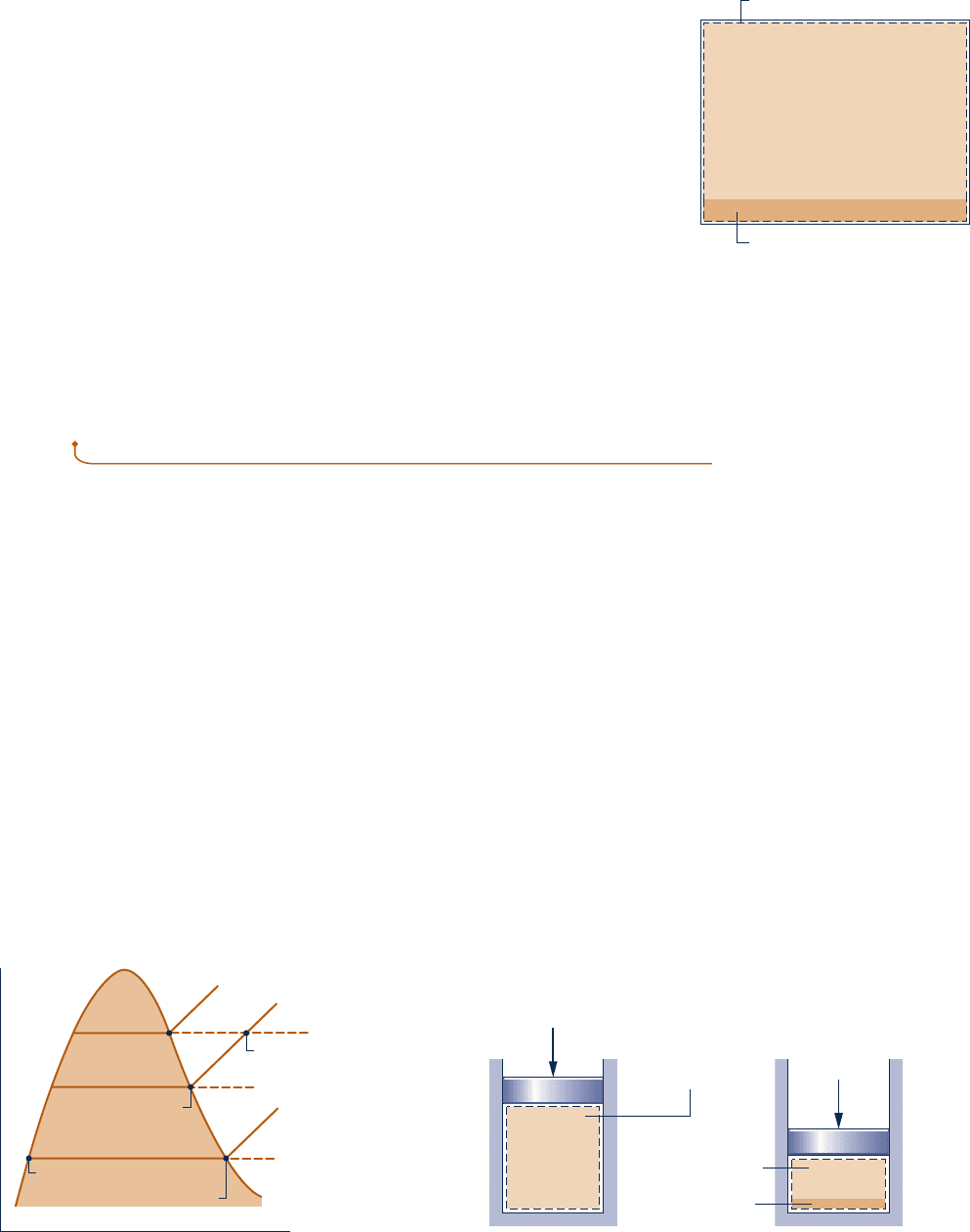
Shown in Fig. 12.5 is a vessel containing liquid water, above which is a mixture
of water vapor and dry air. If no interactions with the surroundings are allowed,
liquid will evaporate until eventually the gas phase becomes saturated and the
system attains an equilibrium state. For many engineering applications, systems
consisting of moist air in equilibrium with a liquid water phase can be described
simply and accurately with the following idealizations:
c The dry air and water vapor behave as independent ideal gases.
c The equilibrium between the liquid phase and the water vapor is not signifi-
cantly disturbed by the presence of the air.
c The partial pressure of the water vapor equals the saturation pressure of water
corresponding to the temperature of the mixture: p
v
5 p
g
(T).
Similar considerations apply for systems consisting of moist air in equilibrium
with a solid water phase. The presence of the air actually alters the partial pressure
of the vapor from the saturation pressure by a small amount whose magnitude is
calculated in Sec. 14.6.
12.5.4
Evaluating the Dew Point Temperature
A significant aspect of the behavior of moist air is that partial condensation of the
water vapor can occur when the temperature is reduced. This type of phenomenon
is commonly encountered in the condensation of vapor on windowpanes and on pipes
carrying cold water. The formation of dew on grass is another familiar example.
To study such condensation, consider a closed system consisting of a sample of moist
air that is cooled at constant pressure, as shown in Fig. 12.6. The property diagram given
on this figure locates states of the water vapor. Initially, the water vapor is superheated
at state 1. In the first part of the cooling process, both the system pressure and the
composition of the moist air remain constant. Accordingly, since p
v
5 y
v
p, the partial
pressure of the water vapor remains constant, and the water vapor cools at constant p
v
from state 1 to state d, called the dew point. The saturation temperature corresponding
to p
v
is called the dew point temperature. This temperature is labeled on Fig. 12.6.
In the next part of the cooling process, the system cools below the dew point
temperature and some of the water vapor initially present condenses. At the final
state, the system consists of a gas phase of dry air and water vapor in equilibrium
with a liquid water phase. In accord with the discussion of Sec. 12.5.3, the vapor that
remains is saturated vapor at the final temperature, state 2 of Fig. 12.6, with a partial
pressure equal to the saturation pressure p
g2
corresponding to this temperature. The
condensate is saturated liquid at the final temperature: state 3 of Fig. 12.6.
System boundary
Liquid water
Gas phase: Dry air and
water vapor
Fig. 12.5 System consisting of
moist air in contact with liquid
water.
T
v
p
g1
p
v1
< p
g1
p
g2
< p
v1
p
p
Initial temperature
Final temperature
Dew point temperature
Initial state
of the water vapor
Dew point
1
d
3
2
Condensate
Final state
of the water vapor
Dry air and
superheated vapor
at the initial temper-
ature
Air and saturated vapor
at final temperature
Condensate:
saturated liquid
at final temperature
Final
state
Initial
state
Fig. 12.6 States of water for moist air cooled at constant mixture pressure.
dew point temperature
12.5 Introducing Psychrometric Principles 731
c12IdealGasMixtureandPsychrometr731 Page 731 6/29/10 11:54:55 AM user-s146c12IdealGasMixtureandPsychrometr731 Page 731 6/29/10 11:54:55 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
732 Chapter 12 Ideal Gas Mixture and Psychrometric Applications
Referring again to Fig. 12.6, note that the partial pressure of the water vapor at
the final state, p
g2
, is less than the initial value, p
v1
. Owing to condensation, the partial
pressure decreases because the amount of water vapor present at the final state is
less than at the initial state. Since the amount of dry air is unchanged, the mole frac-
tion of water vapor in the moist air also decreases.
In the next two examples, we illustrate the use of psychrometric properties intro-
duced thus far. The examples consider, respectively, cooling moist air at constant
pressure and at constant volume.
Cooling Moist Air at Constant Pressure
c c c c EXAMPLE 12.7 c
A 1-lb sample of moist air initially at 708F, 14.7 lbf/in.
2
, and 70% relative humidity is cooled to 408F while keeping
the pressure constant. Determine (a) the initial humidity ratio, (b) the dew point temperature, in 8F, and (c) the
amount of water vapor that condenses, in lb.
SOLUTION
Known:
A 1-lb sample of moist air is cooled at a constant mixture pressure of 14.7 lbf/in.
2
from 70 to 408F. The
initial relative humidity is 70%.
Find: Determine the initial humidity ratio, the dew point temperature, in 8F, and the amount of water vapor that
condenses, in lb.
Schematic and Given Data:
T
v
p
g1
= 0.3632 lbf/in.
2
p
g2
= 0.1217 lbf/in.
2
p
v1
= 0.2542 lbf/in.
2
Dewpoint temperature = 60°F
70°F
40°F
Initial state of vapor
Condensate
Final state
of vapor
m
T
1
1
T
2
= 1 lb
= 70°F
= 70%
= 40°F
φ
Fig. E12.7
Engineering Model:
1.
The 1-lb sample of moist air is taken as the closed system. The system pressure remains constant at 14.7
lbf/in.
2
2. The gas phase can be treated as an ideal gas mixture. The Dalton model applies: Each mixture component
acts as an ideal gas existing alone in the volume occupied by the gas phase at the mixture temperature.
3. When a liquid water phase is present, the water vapor exists as a saturated vapor at the system temperature.
The liquid present is a saturated liquid at the system temperature.
Analysis:
(a)
The initial humidity ratio can be evaluated from Eq. 12.43. This requires the partial pressure of the water
vapor, p
v1
, which can be found from the given relative humidity and p
g
from Table A-2E at 708F as follows
p
v1
5 fp
g
5 10.72
a
0.3632
lbf
in.
2
b
5 0.2542
lbf
in.
2
c12IdealGasMixtureandPsychromet732 Page 732 6/30/10 8:15:29 PM user-s146 c12IdealGasMixtureandPsychromet732 Page 732 6/30/10 8:15:29 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
