Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

536 Chapter 11 Thermodynamic Relations

In this particular example, the ideal gas equation of state gives a value for pressure that exceeds the experimental value by

nearly 16%. Kay’s rule and the rule of additive pressures give pressure values about 3% greater than the experimental value.

The van der Waals equation with mixture values for the constants gives a pressure value about 3% less than the experimen-

tal value.

In the preceding section we considered means for evaluating the p–v–T relation of gas mix-

tures by extending methods developed for pure components. The current section is devoted

to the development of some general aspects of the properties of systems with two or more

components. Primary emphasis is on the case of gas mixtures, but the methods developed

also apply to solutions. When liquids and solids are under consideration, the term solution

is sometimes used in place of mixture. The present discussion is limited to nonreacting mix-

tures or solutions in a single phase. The effects of chemical reactions and equilibrium be-

tween different phases are taken up in Chaps. 13 and 14.

To describe multicomponent systems, composition must be included in our thermody-

namic relations. This leads to the definition and development of several new concepts, in-

cluding the partial molal property, the chemical potential, and the fugacity.

 11.9.1 Partial Molal Properties

In the present discussion we introduce the concept of a partial molal property and illustrate

its use. This concept plays an important role in subsequent discussions of multicomponent

systems.

DEFINING PARTIAL MOLAL PROPERTIES. Any extensive thermodynamic property X of

a single-phase, single-component system is a function of two independent intensive prop-

erties and the size of the system. Selecting temperature and pressure as the independent

properties and the number of moles n as the measure of size, we have X  X(T, p, n). For

a single-phase, multicomponent system, the extensive property X must then be a function

of temperature, pressure, and the number of moles of each component present, X  X(T, p,

, n

, . . . , n

If each mole number is increased by a factor , the size of the system increases by the

same factor, and so does the value of the extensive property X. That is

Differentiating with respect to  while holding temperature, pressure, and the mole numbers

fixed and using the chain rule on the right side gives

This equation holds for all values of . In particular, it holds for   1. Setting   1

(11.101)

where the subscript n

denotes that all n’s except n

are held fixed during differentiation.

X 

i1

T, p, n

X 

0 1an



0 1an



###



0 1an

aX1T, p, n

, n

, . . . , n

2 X1T, p, an

, an

, . . . , an



11.9 Analyzing Multicomponent Systems

This section may be deferred until Secs. 12.1–12.4 have been studied.

solution

11.9 Analyzing Multicomponent Systems 537

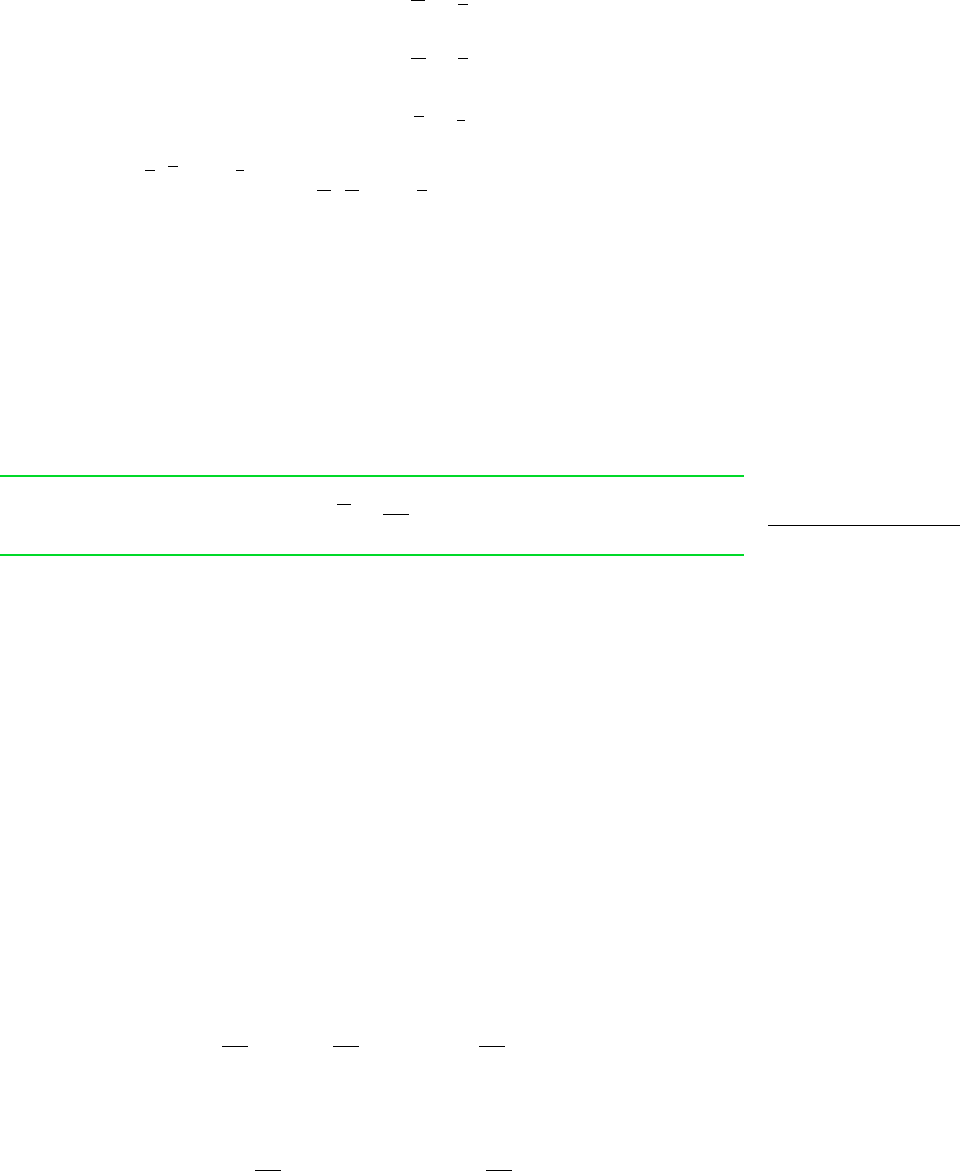
The partial molal property is by definition

(11.102)

The partial molal property is a property of the mixture and not simply a property of

component i, for depends in general on temperature, pressure, and mixture composition:

(T, p, n

, n

, . . . , n

). Partial molal properties are intensive properties of the mixture.

Introducing Eq. 11.102, Eq. 11.101 becomes

(11.103)

This equation shows that the extensive property X can be expressed as a weighted sum of

the partial molal properties .

Selecting the extensive property X in Eq. 11.103 to be volume, internal energy, enthalpy,

and entropy, respectively, gives

(11.104)

where denote the partial molal volume, internal energy, enthalpy, and entropy.

Similar expressions can be written for the Gibbs function G and the Helmholtz function .

Moreover, the relations between these extensive properties: H  U  pV, G  H  TS, 

U  TS can be differentiated with respect to n

while holding temperature, pressure, and the

remaining n’s constant to produce corresponding relations among partial molal properties:

where are the partial molal Gibbs

function and Helmholtz function, respectively. Several additional relations involving partial mo-

lal properties are developed later in this section.

EVALUATING PARTIAL MOLAL PROPERTIES. Partial molal properties can be evaluated by

several methods, including the following:

 If the property X can be measured, can be found by extrapolating a plot giving

(Xn

)

T, p, n

versus n

. That is

 If an expression for X in terms of its independent variables is known, can be evalu-

ated by differentiation. The derivative can be determined analytically if the function is

expressed analytically or found numerically if the function is in tabular form.

 When suitable data are available, a simple graphical procedure known as the method of

intercepts can be used to evaluate partial molal properties. In principle, the method can

be applied for any extensive property. To introduce this method, let us consider the vol-

ume of a system consisting of two components, A and B. For this system, Eq. 11.103

takes the form

where are the partial molal volumes of A and B, respectively. Dividing by the

number of moles of mixture n

 y

 y

and V

V  n

 n

 a

T, p, n

 lim

¢n

S 0

¢X

¢n

T, p, n

and °

 U

 pV

, G

 H

 TS

, °

 U

 TS

, U

, H

, S

V 

i1

U 

i1

H 

i1

S 

i1

X 

i1



T, p, n

partial molal property

method of intercepts

538 Chapter 11 Thermodynamic Relations

where y

and y

denote the mole fractions of A and B, respectively. Since y

 y

 1,

this becomes

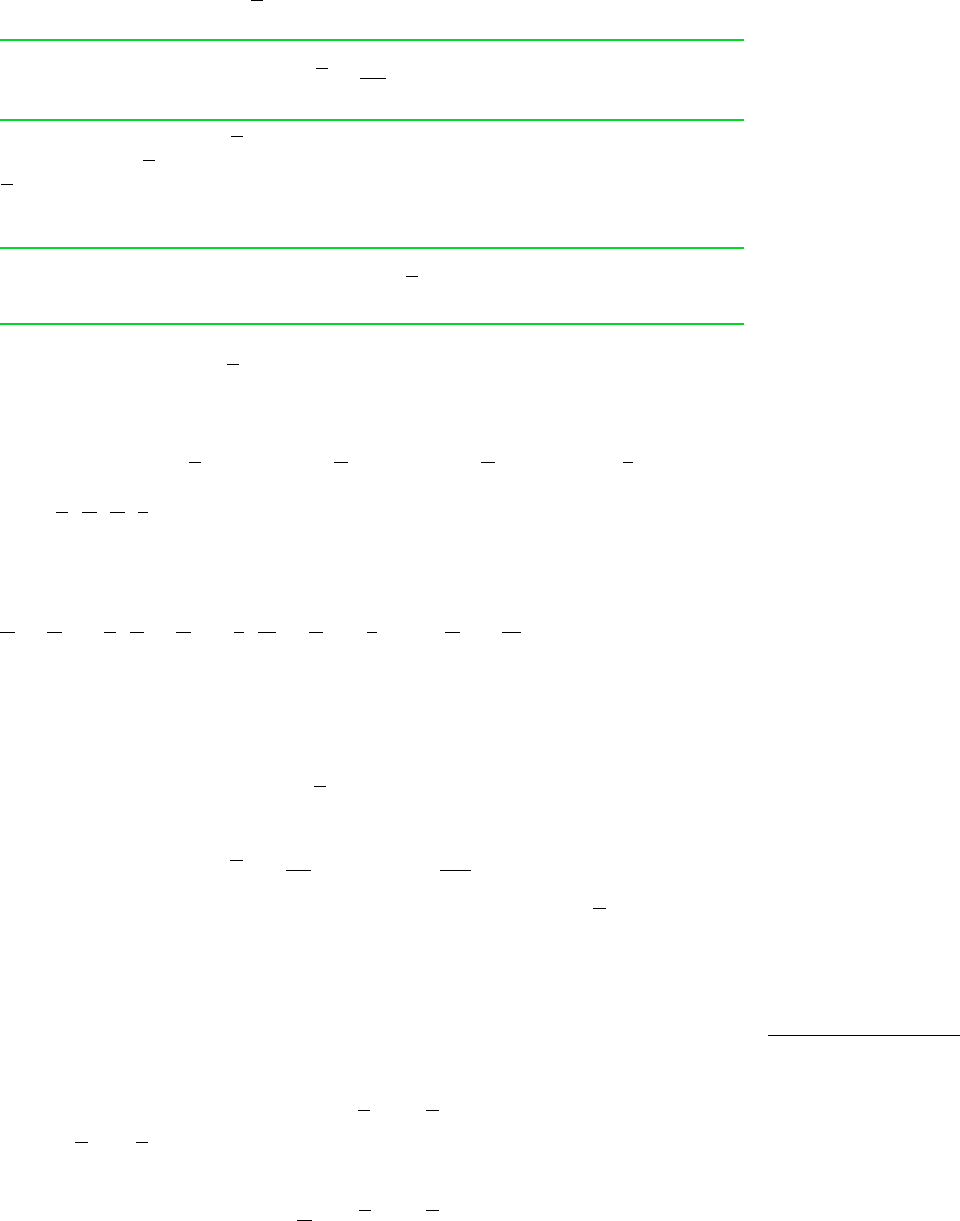
This equation provides the basis for the method of intercepts. For example, refer to

Fig. 11.5, in which Vn is plotted as a function of y

at constant T and p. At a speci-

fied value for y

, a tangent to the curve is shown on the figure. When extrapolated,

the tangent line intersects the axis on the left at and the axis on the right at

These values for the partial molal volumes correspond to the particular specifications

for T, p, and y

. At fixed temperature and pressure, and vary with y

and are

not equal to the molar specific volumes of pure A and pure B, denoted on the figure

as and respectively. The values of and are fixed by temperature and

pressure only.

EXTENSIVE PROPERTY CHANGES ON MIXING. Let us conclude the present discussion

by evaluating the change in volume on mixing of pure components at the same temperature

and pressure, a result for which an application is given later in the section. The total volume

of the pure components before mixing is

where is the molar specific volume of pure component i. The volume of the mixture is

where is the partial molal volume of component i in the mixture. The volume change on

mixing is

(11.105)¢V

mixing



i1

 v

¢V

mixing

 V

mixture

 V

components



i1



i1

mixture



i1

components



i1

 11  y

 y

 V

 y

 V

––

T and p constant

as a function of y

(T, p)

(T, p, y

)

(pure A)

1.0

(pure B)

Mole fraction of B

Tangent

line

(T, p)

(T, p, y

)

 Figure 11.5 Illustration of the evaluation

of partial molal volumes by the method of in-

tercepts.

11.9 Analyzing Multicomponent Systems 539

Similar results can be obtained for other extensive properties, for example,

(11.106)

In Eqs. 11.106, and denote the molar internal energy, enthalpy, and entropy

of pure component i. The symbols and denote the respective partial molal

properties.

 11.9.2 Chemical Potential

Of the partial molal properties, the partial molal Gibbs function is particularly useful in de-

scribing the behavior of mixtures and solutions. This quantity plays a central role in the cri-

teria for both chemical and phase equilibrium (Chap. 14). Because of its importance in the

study of multicomponent systems, the partial molal Gibbs function of component i is given

a special name and symbol. It is called the chemical potential of component i and sym-

bolized by 

(11.107)

Like temperature and pressure, the chemical potential 

is an intensive property.

Applying Eq. 11.103 together with Eq. 11.107, the following expression can be written:

(11.108)

Expressions for the internal energy, enthalpy, and Helmholtz function can be obtained

from Eq. 11.108, using the definitions H  U  pV, G  H  TS, and U  TS.

They are

(11.109)

Other useful relations can be obtained as well. Forming the differential of G(T, p,

, n

, . . . , n

)

(11.110)

The subscripts n in the first two terms indicate that all n’s are held fixed during differentia-

tion. Since this implies fixed composition, it follows from Eqs. 11.30 and 11.31 that

(11.111)

V  a

T, n

and

S  a

p, n

dG 

T, n

dp 

p, n

dT 

i1

T, p, n

° pV 

i1

H  TS 

i1

U  TS  pV 

i1

G 

i1

 G



T, p, n

, H

, h

¢S

mixing



i1

 s

¢H

mixing



i1

 h

¢U

mixing



i1

 u

chemical potential

540 Chapter 11 Thermodynamic Relations

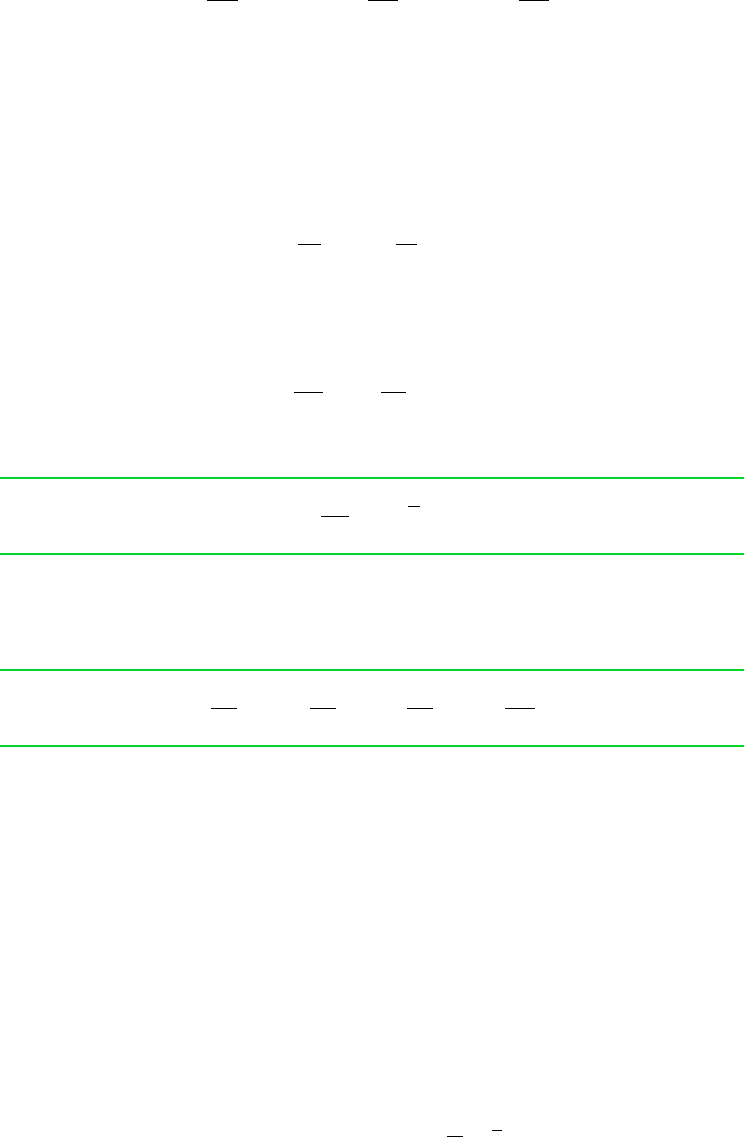
With Eqs. 11.107 and 11.111, Eq. 11.110 becomes

(11.112)

which for a multicomponent system is the counterpart of Eq. 11.23.

Another expression for dG is obtained by forming the differential of Eq. 11.108. That is

Combining this equation with Eq. 11.112 gives the Gibbs–Duhem equation

(11.113)

 11.9.3 Fundamental Thermodynamic Functions for

Multicomponent Systems

A fundamental thermodynamic function provides a complete description of the thermody-

namic state of a system. In principle, all properties of interest can be determined from such

a function by differentiation and/or combination. Reviewing the developments of Sec. 11.9.2,

we see that a function G(T, p, n

, n

, . . . , n

) is a fundamental thermodynamic function for

a multicomponent system.

Functions of the form U(S, V, n

, n

,... ,n

), H(S, p, n

, n

,... ,n

), and (T, V,

, n

,... ,n

) also can serve as fundamental thermodynamic functions for multicomponent

systems. To demonstrate this, first form the differential of each of Eqs. 11.109 and use the

Gibbs–Duhem equation, Eq. 11.113, to reduce the resultant expressions to obtain

(11.114a)

(11.114b)

(11.114c)

For multicomponent systems, these are the counterparts of Eqs. 11.18, 11.19, and 11.22,

respectively.

The differential of U(S, V, n

, n

,... ,n

) is

Comparing this expression term by term with Eq. 11.114a, we have

(11.115a)

That is, the temperature, pressure, and chemical potentials can be obtained by differentiation

of U(S, V, n

, n

,... ,n

). The first two of Eqs. 11.115a are the counterparts of Eqs. 11.24

and 11.25.

A similar procedure using a function of the form H(S, p, n

, n

,... ,n

) together with

Eq. 11.114b gives

(11.115b)

T 

p, n

V 

S, n



S, p, n

T 

V, n

p 

S, n



S,V, n

dU 

V, n

dS 

S, n

dV 

i1

S,V, n

d° p dV  S dT 

i1

dH  T dS  V dp 

i1

dU  T dS  p dV 

i1

 V dp  S dT

dG 

i1



i1

dG  V dp  S dT 

i1

Gibbs–Duhem equation

11.9 Analyzing Multicomponent Systems 541

where the first two of these are the counterparts of Eqs. 11.26 and 11.27. Finally, with

(S, V, n

, n

,... ,n

) and Eq. 11.114c

(11.115c)

The first two of these are the counterparts of Eqs. 11.28 and 11.29. With each choice of fun-

damental function, the remaining extensive properties can be found by combination using

the definitions H  U  pV, G  H  TS, U  TS.

The foregoing discussion of fundamental thermodynamic functions has led to several prop-

erty relations for multicomponent systems that correspond to relations obtained previously.

In addition, counterparts of the Maxwell relations can be obtained by equating mixed sec-

ond partial derivatives. For example, the first two terms on the right of Eq. 11.112 give

(11.116)

which corresponds to Eq. 11.35. Numerous relationships involving chemical potentials can

be derived similarly by equating mixed second partial derivatives. An important example

from Eq. 11.112 is

Recognizing the right side of this equation as the partial molal volume, we have

(11.117)

This relationship is applied later in the section.

The present discussion concludes by listing four different expressions derived above for

the chemical potential in terms of other properties. In the order obtained, they are

(11.118)

Only the first of these partial derivatives is a partial molal property, however, for the term

partial molal applies only to partial derivatives where the independent variables are temper-

ature, pressure, and the number of moles of each component present.

 11.9.4 Fugacity

The chemical potential plays an important role in describing multicomponent systems. In

some instances, however, it is more convenient to work in terms of a related property, the

fugacity. The fugacity is introduced in the present discussion.

SINGLE-COMPONENT SYSTEMS

Let us begin by taking up the case of a system consisting of a single component. For this

case, Eq. 11.108 reduces to give

G  nm

m 

 g



T, p, n



S,V, n



S, p, n



0°

T,V, n

T, n

 V

T, n



T, p, n

p, n



T, n

p 

0°

T, n

S 

0°

V, n



0°

T,V, n

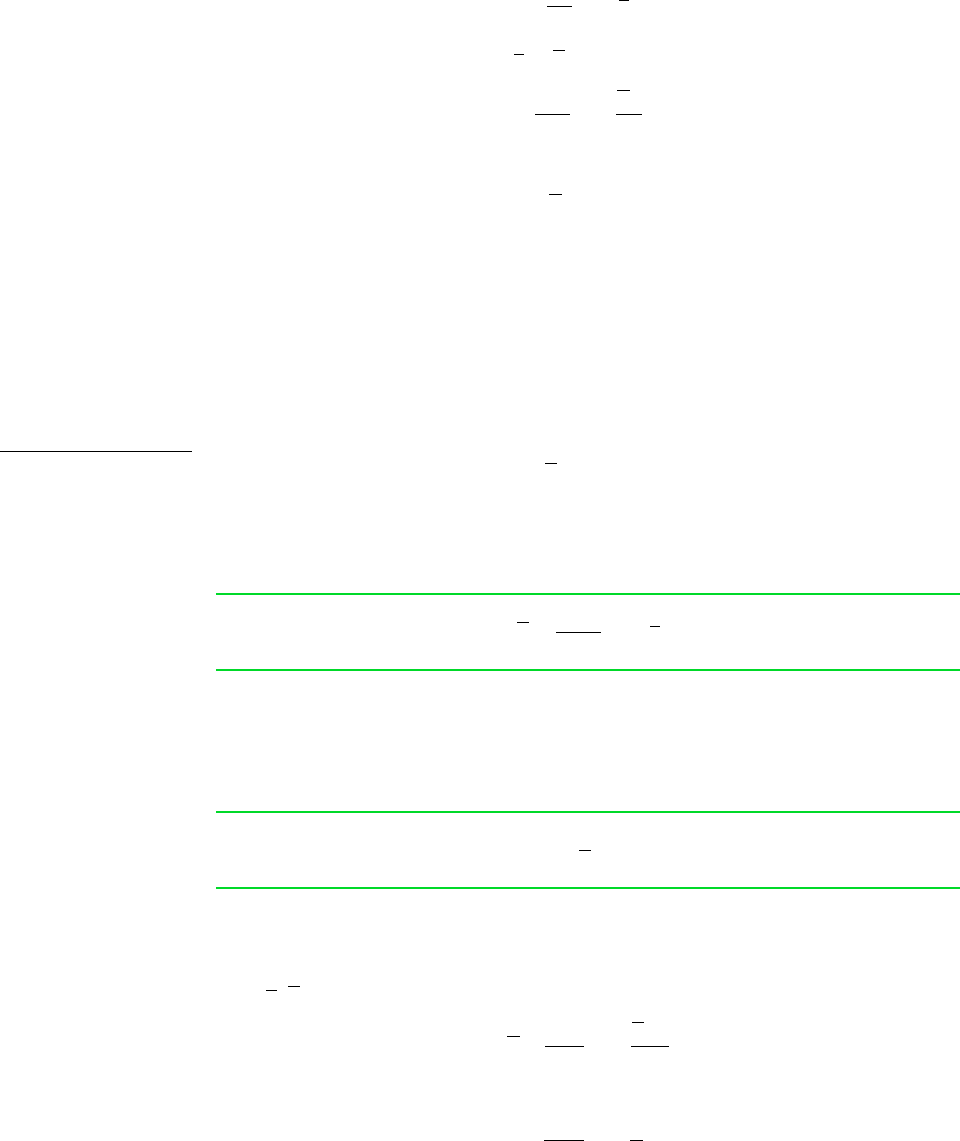
That is, for a pure component the chemical potential equals the Gibbs function per mole.

With this equation, Eq. 11.30 written on a per mole basis becomes

(11.119)

For the special case of an ideal gas, and Eq. 11.119 assumes the form

where the asterisk denotes ideal gas. Integrating at constant temperature

(11.120)

where C(T) is a function of integration. Since the pressure p can take on values from zero

to plus infinity, the ln p term of this expression, and thus the chemical potential, has an in-

convenient range of values from minus infinity to plus infinity. Equation 11.120 also shows

that the chemical potential can be determined only to within an arbitrary constant.

INTRODUCING FUGACITY. Because of the above considerations, it is advantageous for

many types of thermodynamic analyses to use fugacity in place of the chemical potential,

for it is a well-behaved function that can be more conveniently evaluated. We introduce the

fugacity f by the expression

(11.121)

Comparing Eq. 11.121 with Eq. 11.120, the fugacity is seen to play the same role in the gen-

eral case as pressure plays in the ideal gas case. Fugacity has the same units as pressure.

Substituting Eq. 11.121 into Eq. 11.119 gives

(11.122)

Integration of Eq. 11.122 while holding temperature constant can determine the fugacity only

to within a constant term. However, since ideal gas behavior is approached as pressure tends

to zero, the constant term can be fixed by requiring that the fugacity of a pure component

equals the pressure in the limit of zero pressure. That is

(11.123)

Equations 11.122 and 11.123 then completely determine the fugacity function.

EVALUATING FUGACITY. Let us consider next how the fugacity can be evaluated. With

Eq. 11.122 becomes

ln f



T a

0 ln f



RTZ

Z  pv



RT,

lim

pS 0

 1

T a

0 ln f

 v

m  RT ln f  C 1T 2

m*  R

T ln p  C 1T 2

0m*



 RT



 v

542 Chapter 11 Thermodynamic Relations

fugacity

11.9 Analyzing Multicomponent Systems 543

Subtracting 1p from both sides and integrating from pressure p to pressure p at fixed tem-

perature T

Taking the limit as p tends to zero and applying Eq. 11.123 results in

When expressed in terms of the reduced pressure, p

 pp

, the above equation is

(11.124)

Since the compressibility factor Z depends on the reduced temperature T

and reduced pres-

sure p

, it follows that the right side of Eq. 11.124 depends on these properties only. Ac-

cordingly, the quantity ln fp is a function only of these two reduced properties. Using a gen-

eralized equation of state giving Z as a function of T

and p

, ln fp can readily be evaluated

with a computer. Tabular representations are also found in the literature. Alternatively, the

graphical representation presented in Fig. A-6 can be employed.

 for example. . . to illustrate the use of Fig. A-6, consider two states of water vapor

at the same temperature, 400C. At state 1 the pressure is 200 bar, and at state 2 the pres-

sure is 240 bar. The change in the chemical potential between these states can be determined

using Eq. 11.121 as

Using the critical temperature and pressure of water from Table A-1, at state 1 p

 0.91,

 1.04, and at state 2 p

 1.09, T

 1.04. By inspection of Fig. A-6, f

p

 0.755

and f

p

 0.7. Inserting values in the above equation

For a pure component, the chemical potential equals the Gibbs function per mole,

Since the temperature is the same at states 1 and 2, the change in the chemi-

cal potential can be expressed as Using steam table data,

the value obtained with this expression is 597 kJ/kmol, which agrees with the value deter-

mined from the generalized fugacity coefficient chart. 

MULTICOMPONENT SYSTEMS

The fugacity of a component i in a mixture can be defined by a procedure that parallels the

definition for a pure component. For a pure component, the development begins with

Eq. 11.119, and the fugacity is introduced by Eq. 11.121. These are then used to write the

pair of equations, Eqs. 11.122 and 11.123, from which the fugacity can be evaluated. For a

 m

 h

 h

 T 1s

 s

g  h  T s.

 m

 18.31421673.152 ln c10.72 a

240

200

b a

0.755

bd 597 kJ/kmol

 m

 RT ln

 RT ln a





1Z  12 d ln p





1Z  12 d ln p

cln

p¿





p¿

1Z  12 d ln p

3ln f  ln p4

p¿





p¿

1Z  12 d ln p

mixture, the development begins with Eq. 11.117, the counterpart of Eq. 11.119, and the

fugacity of component i is introduced by

(11.125)

which parallels Eq. 11.121. The pair of equations that allow the fugacity of a mixture

component, to be evaluated are

(11.126a)

(11.126b)

The symbol denotes the fugacity of component i in the mixture and should be carefully

distinguished in the presentation to follow from f

, which denotes the fugacity of pure i.

DISCUSSION. Referring to Eq. 11.126b, note that in the ideal gas limit the fugacity is

not required to equal the pressure p as for the case of a pure component, but to equal the

quantity y

p. To see that this is the appropriate limiting quantity, consider a system consist-

ing of a mixture of gases occupying a volume V at pressure p and temperature T. If the over-

all mixture behaves as an ideal gas, we can write

(11.127)

where n is the total number of moles of mixture. Recalling from Sec. 3.5 that an ideal gas can

be regarded as composed of molecules that exert negligible forces on one another and whose

volume is negligible relative to the total volume, we can think of each component i as be-

having as if it were an ideal gas alone at the temperature T and volume V. Thus, the pressure

exerted by component i would not be the mixture pressure p but the pressure p

given by

(11.128)

where n

is the number of moles of component i. Dividing Eq. 11.128 by Eq. 11.127

On rearrangement

(11.129)

Accordingly, the quantity y

p appearing in Eq. 11.126b corresponds to the pressure p

Summing both sides of Eq. 11.129, we obtain

Or, since the sum of the mole fractions equals unity

(11.130)

In words, Eq. 11.130 states that the sum of the pressures p

equals the mixture pressure. This

gives rise to the designation partial pressure for p

. With this background, we now see that

p 

i1



i1

p  p

i1

 y





nRT





 y



p 

nRT

lim

pS0

b 1

T a

0 ln f

T, n

 V

 RT ln f

 C

1T 2

544 Chapter 11 Thermodynamic Relations

fugacity of a mixture

component

11.9 Analyzing Multicomponent Systems 545

Eq. 11.126b requires the fugacity of component i to approach the partial pressure of com-

ponent i as pressure p tends to zero. Comparing Eqs. 11.130 and 11.99a, we also see that

the additive pressure rule is exact for ideal gas mixtures. This special case is considered fur-

ther in Sec. 12.2 under the heading Dalton model.

EVALUATING FUGACITY IN A MIXTURE. Let us consider next how the fugacity of com-

ponent i in a mixture can be expressed in terms of quantities that can be evaluated. For a

pure component i, Eq. 11.122 gives

(11.131)

where is the molar specific volume of pure i. Subtracting Eq. 11.131 from Eq. 11.126a

(11.132)

Integrating from pressure p¿ to pressure p at fixed temperature and mixture composition

In the limit as p¿ tends to zero, this becomes

Since and as pressure p¿ tends to zero

Therefore, we can write

(11.133)

in which is the fugacity of component i at pressure p in a mixture of given composition

at a given temperature, and f

is the fugacity of pure i at the same temperature and pressure.

Equation 11.133 expresses the relation between and f

in terms of the difference between

and a measurable quantity.

 11.9.5 Ideal Solution

The task of evaluating the fugacities of the components in a mixture is considerably simpli-

fied when the mixture can be modeled as an ideal solution. An ideal solution is a mixture

for which

(11.134)

 y

1ideal solution2

RT ln a

b



 v

2 dp

RT cln a

b ln y

d



 v

2 dp

lim

p¿ S 0

ln a

bS ln a

p¿

b ln y

S y

p¿f

S p¿

RT cln a

b lim

p¿ S 0

ln a

bd



 v

2 dp

T cln a

p¿





p¿

 v

T c

0 ln 1



T, n

 V

 v

RT a

0 ln f

 v

Lewis–Randall rule

ideal solution