Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

506 Chapter 11 Thermodynamic Relations

where  and  denote the respective phases, and (dpdT )

sat

is the slope of the relevant satu-

ration pressure–temperature curve.

The Clapeyron equation shows that the slope of a saturation line on a phase diagram de-

pends on the signs of the specific volume and enthalpy changes accompanying the phase

change. In most cases, when a phase change takes place with an increase in specific enthalpy,

the specific volume also increases, and (dpdT )

sat

is positive. However, in the case of the

melting of ice and a few other substances, the specific volume decreases on melting. The

slope of the saturated solid–liquid curve for these few substances is negative, as was pointed

out in Sec. 3.2.2 in the discussion of phase diagrams.

An approximate form of Eq. 11.40 can be derived when the following two idealizations

are justified: (1) v

is negligible in comparison to v

, and (2) the pressure is low enough that

can be evaluated from the ideal gas equation of state as v

 RTp. With these, Eq. 11.40

becomes

which can be rearranged to read

(11.42)

Equation 11.42 is called the Clausius–Clapeyron equation. A similar expression applies for

the case of sublimation.

The use of the Clapeyron equation in any of the foregoing forms requires an accurate rep-

resentation for the relevant saturation pressure–temperature curve. This must not only depict

the pressure–temperature variation accurately but also enable accurate values of the deriva-

tive (dpdT )

sat

to be determined. Analytical representations in the form of equations are com-

monly used. Different equations for different portions of the pressure–temperature curves

may be required. These equations can involve several constants. One form that is used for

the vapor-pressure curves is the four-constant equation

in which the constants A, B, C, D are determined empirically.

The use of the Clapeyron equation for evaluating changes in specific entropy, internal en-

ergy, and enthalpy accompanying a phase change at fixed T and p is illustrated in the next

example.

ln p

sat

 A 

 C ln T  DT

d ln p

sat



 h

sat



 h



EXAMPLE 11.4 Applying the Clapeyron Equation

Using p–v–T data for saturated water, calculate at 100C (a) h

 h

, (b) u

 u

, (c) s

 s

. Compare with the respective

steam table value.

SOLUTION

Known: The system consists of a unit mass of saturated water at 100C.

Find: Using saturation data, determine at 100C the change on vaporization of the specific enthalpy, specific internal energy,

and specific entropy, and compare with the respective steam table value.

Analysis: For comparison, Table A-2 gives at 100C, h

 h

 2257.0 kJ/kg, u

 u

 2087.6 kg/kg, s

 s

 6.048

kJ/kg K.

Clausius–Clapeyron

equation

11.4 Evaluating Changes in Entropy, Internal Energy, and Enthalpy 507

(a) The value of h

 h

can be determined from the Clapeyron equation, Eq. 11.40, expressed as

This equation requires a value for the slope (dpdT)

sat

of the saturation pressure–temperature curve at the specified temperature.

The required value for (dpdT )

sat

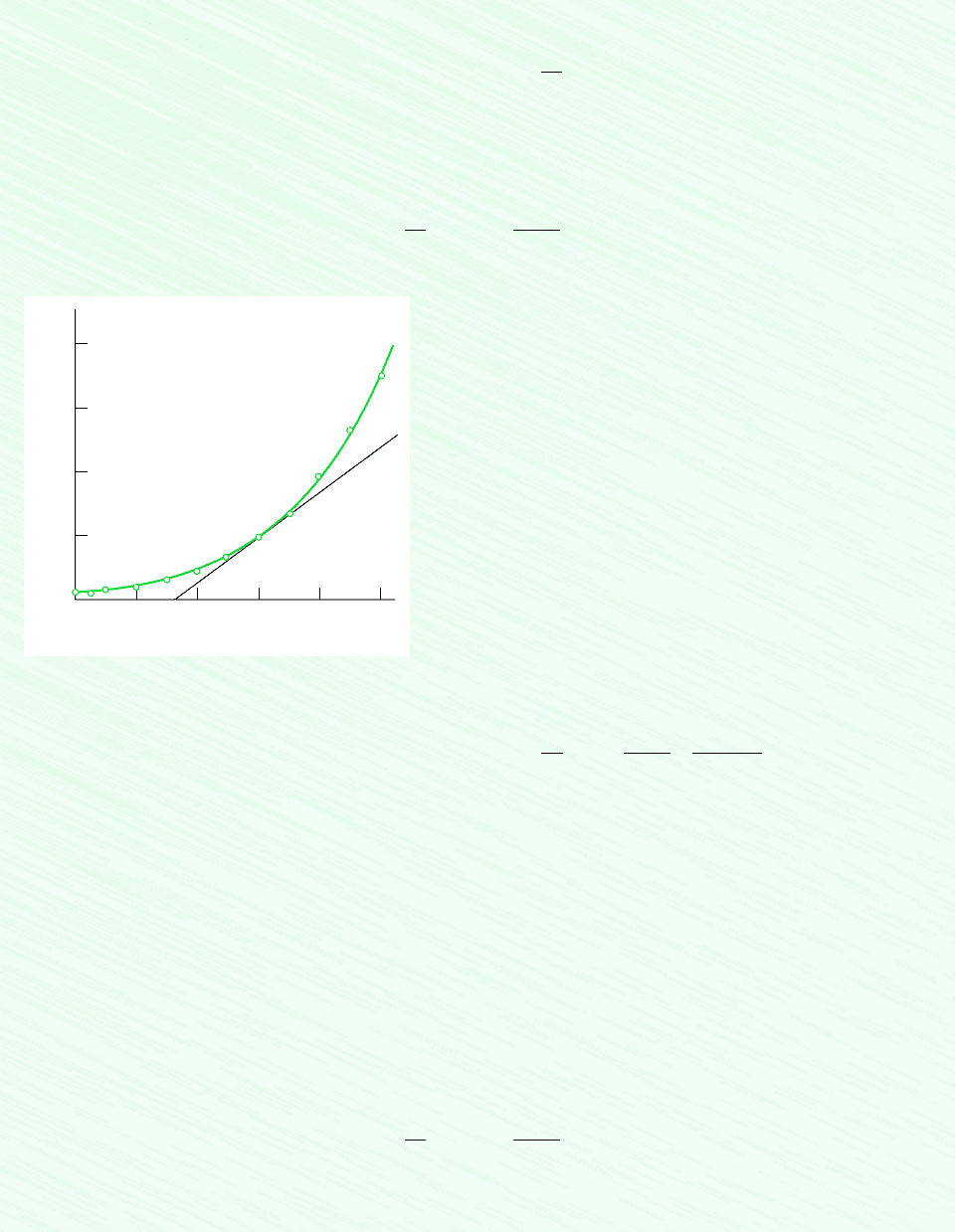
at 100C can be estimated graphically as follows. Using saturation pressure–temperature

data from the steam tables, the accompanying plot can be prepared. Note that a line drawn tangent to the curve at 100C is

shown on the plot. The slope of this tangent line is about 3570 N/m

K. Accordingly, at 100C

sat

 3570

 h

 T 1v

 v

2 a

sat

Saturation pressure (bar)

40 60 80 100 120 140

Temperature (°C)

 Figure E11.4

Inserting values into the above equation for h

 h

gives

This value is about 1% less than the value read from the steam tables.

Alternatively, the derivative (dpdT )

sat

can be estimated using numerical methods and computer-generated data. The fol-

lowing IT code illustrates one way the derivative, denoted dpdT, can be estimated:

T = 100 // C

dT = 0.001

T1 = T – dT

T2 = T + dT

p1 = Psat(“Water/Steam”, T1) // bar

p2 = Psat(“Water/Steam”, T2) // bar

dpdT = ((p2 – p1) / (T2 – T1)) * 100000

Using the Explore button, sweep dT from 0.001 to 0.01 in steps of 0.001. Then, reading the limiting value from the computer

data

When this value is used in the above expression for h

 h

, the result is h

 h

 2256 kJ/kg, which agrees very closely

with the value read from the steam tables.

sat

 3616

 2227 kJ/kg

 h

 1373.15 K2 11.673  1.0435  10

3

2 a

a3570

b `

1 kJ

❶

508 Chapter 11 Thermodynamic Relations

(b) With Eq. 11.39

Inserting the IT result for (h

 h

) from part (a) together with saturation data at 100C

which also agrees closely with the value from the steam tables.

 h

) from part (a)

which again agrees very closely with the steam table value.

Also, (dpdT)

sat

might be obtained by differentiating an analytical expression for the vapor pressure curve, as discussed in

Sec. 11.4.1 above.

 s



 h



2256 kJ/kg

373.15 K

 6.046

 2086.5

 u

 2256

 a1.014  10

b a1.672

b `

1 kJ

 u

 h

 h

 p

sat

 v

❶

 11.4.2 Considering Single-Phase Regions

The objective of the present section is to derive expressions for evaluating s, u, and h

between states in single-phase regions. These expressions require both p–v–T data and ap-

propriate specific heat data. Since single-phase regions are under present consideration, any

two of the properties pressure, specific volume, and temperature can be regarded as the in-

dependent properties that fix the state. Two convenient choices are T, v and T, p.

T AND v AS INDEPENDENT PROPERTIES. With temperature and specific volume as the

independent properties that fix the state, the specific entropy can be regarded as a function

of the form s  s(T, v). The differential of this function is

The partial derivative ( s v)

appearing in this expression can be replaced using the Maxwell

relation, Eq. 11.34, giving

(11.43)

The specific internal energy also can be regarded as a function of T and v: u  u(T, v).

The differential of this function is

With c

 ( u T )

(11.44)du  c

dT  a

du  a

dT  a

ds  a

dT  a

ds  a

dT  a

11.4 Evaluating Changes in Entropy, Internal Energy, and Enthalpy 509

Substituting Eqs. 11.43 and 11.44 into du  T ds  p dv and collecting terms results in

(11.45)

Since specific volume and temperature can be varied independently, let us hold specific vol-

ume constant and vary temperature. That is, let dv  0 and dT 0. It then follows from

Eq. 11.45 that

(11.46)

Similarly, suppose that dT  0 and dv 0. It then follows that

(11.47)

Equations 11.46 and 11.47 are additional examples of useful thermodynamic property

relations.  for example. . . Equation 11.47, which expresses the dependence of the spe-

cific internal energy on specific volume at fixed temperature, allows us to demonstrate that the

internal energy of a gas whose equation of state is pv  RT depends on temperature alone,

a result first discussed in Sec. 3.5. Equation 11.47 requires the partial derivative ( p T )

If p  RTv, the derivative is ( p T )

 Rv. Introducing this, Eq. 11.47 gives

This demonstrates that when pv  RT, the specific internal energy is independent of specific

volume and depends on temperature alone.



Continuing the discussion, when Eq. 11.46 is inserted in Eq. 11.43, the following ex-

pression results

(11.48)

Inserting Eq. 11.47 into Eq. 11.44 gives

(11.49)

Observe that the right sides of Eqs. 11.48 and 11.49 are expressed solely in terms of p, v, T,

and c

Changes in specific entropy and internal energy between two states are determined by in-

tegration of Eqs. 11.48 and 11.49, respectively

(11.50)

(11.51)

To integrate the first term on the right of each of these expressions, the variation of c

with temperature at one fixed specific volume (isometric) is required. Integration of the

 u





dT 



cT a

 p d dv

 s





dT 



du  c

dT  cT a

 p d dv

ds 

dT  a

 T a

 p  T a

b p  p  p  0

 T a

 p







 p  T a

d dv  cT a

 c

d dT

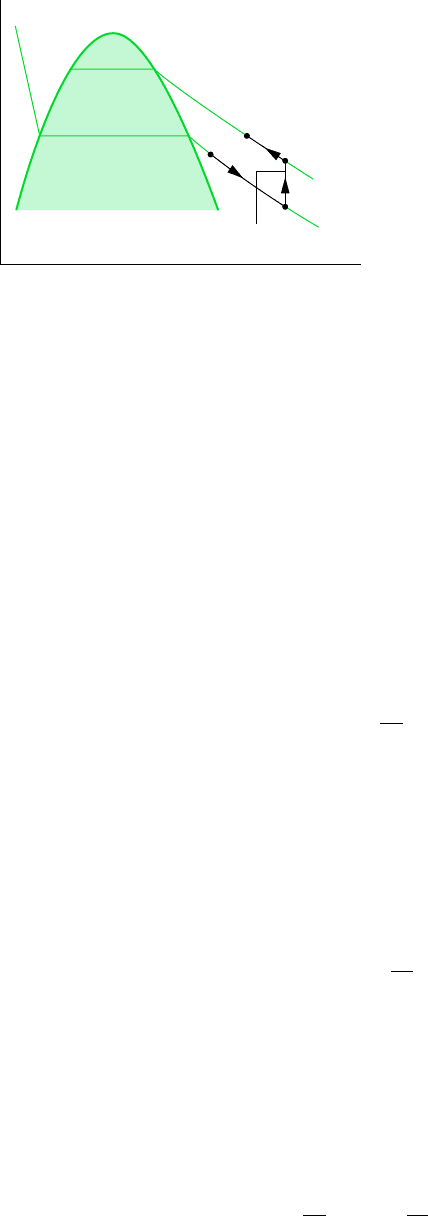
510 Chapter 11 Thermodynamic Relations

second term requires knowledge of the p–v–T relation at the states of interest. An equa-

tion of state explicit in pressure would be particularly convenient for evaluating the inte-

grals involving ( p T)

. The accuracy of the resulting specific entropy and internal en-

ergy changes would depend on the accuracy of this derivative. In cases where the

integrands of Eqs. 11.50 and 11.51 are too complicated to be integrated in closed form

they may be evaluated numerically. Whether closed-form or numerical integration is used,

attention must be given to the path of integration.

 for example. . . let us consider the evaluation of Eq. 11.51. Referring to Fig. 11.2,

if the specific heat c

is known as a function of temperature along the isometric (constant

specific volume) passing through the states x and y, one possible path of integration for de-

termining the change in specific internal energy between states 1 and 2 is 1–x–y–2. The in-

tegration would be performed in three steps. Since the temperature is constant from state 1

to state x, the first integral of Eq. 11.51 would vanish, so

From state x to y, the specific volume is constant and c

is known as a function of temper-

ature only, so

where T

 T

and T

 T

. From state y to state 2, the temperature is constant once again,

and

When these are added, the result is the change in specific internal energy between states 1

and 2. 

T AND p AS INDEPENDENT PROPERTIES. In this section a presentation parallel to that

considered above is provided for the choice of temperature and pressure as the independent

properties. With this choice for the independent properties, the specific entropy can be re-

garded as a function of the form s  s(T, p). The differential of this function is

ds  a

dT  a

 u





 v

cT a

 p d dv

 u





 u





cT a

 p d dv

= v

= T

= c

(T, v

)

 Figure 11.2

Integration path between

two vapor states.

11.4 Evaluating Changes in Entropy, Internal Energy, and Enthalpy 511

The partial derivative ( )

appearing in this expression can be replaced using the Maxwell

relation, Eq. 11.35, giving

(11.52)

The specific enthalpy also can be regarded as a function of T and p: h  h(T, p). The dif-

ferential of this function is

With

(11.53)

Substituting Eqs. 11.52 and 11.53 into dh  T ds  v dp and collecting terms results in

(11.54)

Since pressure and temperature can be varied independently, let us hold pressure constant

and vary temperature. That is, let dp  0 and It then follows from Eq. 11.54 that

(11.55)

Similarly, when dT  0 and Eq. 11.54 gives

(11.56)

Equations 11.55 and 11.56, like Eqs. 11.46 and 11.47, are useful thermodynamic property

relations.

When Eq. 11.55 is inserted in Eq. 11.52, the following equation results:

(11.57)

Introducing Eq. 11.56 into Eq. 11.53 gives

(11.58)

Observe that the right sides of Eqs. 11.57 and 11.58 are expressed solely in terms of p, v, T,

and c

Changes in specific entropy and enthalpy between two states are found by integrating

Eqs. 11.57 and 11.58, respectively

(11.59)

(11.60) h

 h





dT 



cv  T a

d dp

 s





dT 



dh  c

dT  cv  T a

d dp

ds 

dT  a

 v  T a

dp  0,



dT  0.

 T a

 v d dp  cT a

 c

dh  c

dT  a

 (0h



0T )

dh  a

dT  a

ds  a

dT  a



512 Chapter 11 Thermodynamic Relations

To integrate the first term on the right of each of these expressions, the variation of c

with

temperature at one fixed pressure (isobar) is required. Integration of the second term requires

knowledge of the p–v–T behavior at the states of interest. An equation of state explicit in v

would be particularly convenient for evaluating the integrals involving ( )

. The accu-

racy of the resulting specific entropy and enthalpy changes would depend on the accuracy

of this derivative.

Changes in specific enthalpy and internal energy are related through h  u  pv by

(11.61)

Hence, only one of h and u need be found by integration. Then, the other can be eval-

uated from Eq. 11.61. Which of the two property changes is found by integration depends

on the information available. h would be found using Eq. 11.60 when an equation of

state explicit in v and c

as a function of temperature at some fixed pressure are known.

u would be found from Eq. 11.51 when an equation of state explicit in p and c

as a

function of temperature at some specific volume are known. Such issues are considered

in Example 11.5.

 h

 1u

 u

2 1p

 p



EXAMPLE 11.5 Evaluating ⌬s, ⌬u, and ⌬h of a Gas

Using the Redlich–Kwong equation of state, develop expressions for the changes in specific entropy, internal energy, and en-

thalpy of a gas between two states where the temperature is the same, T

 T

, and the pressures are p

and p

, respectively.

SOLUTION

Known: Two states of a unit mass of a gas as the system are fixed by p

and T

at state 1 and p

, T

( T

) at state 2.

Find: Determine the changes in specific entropy, internal energy, and enthalpy between these two states.

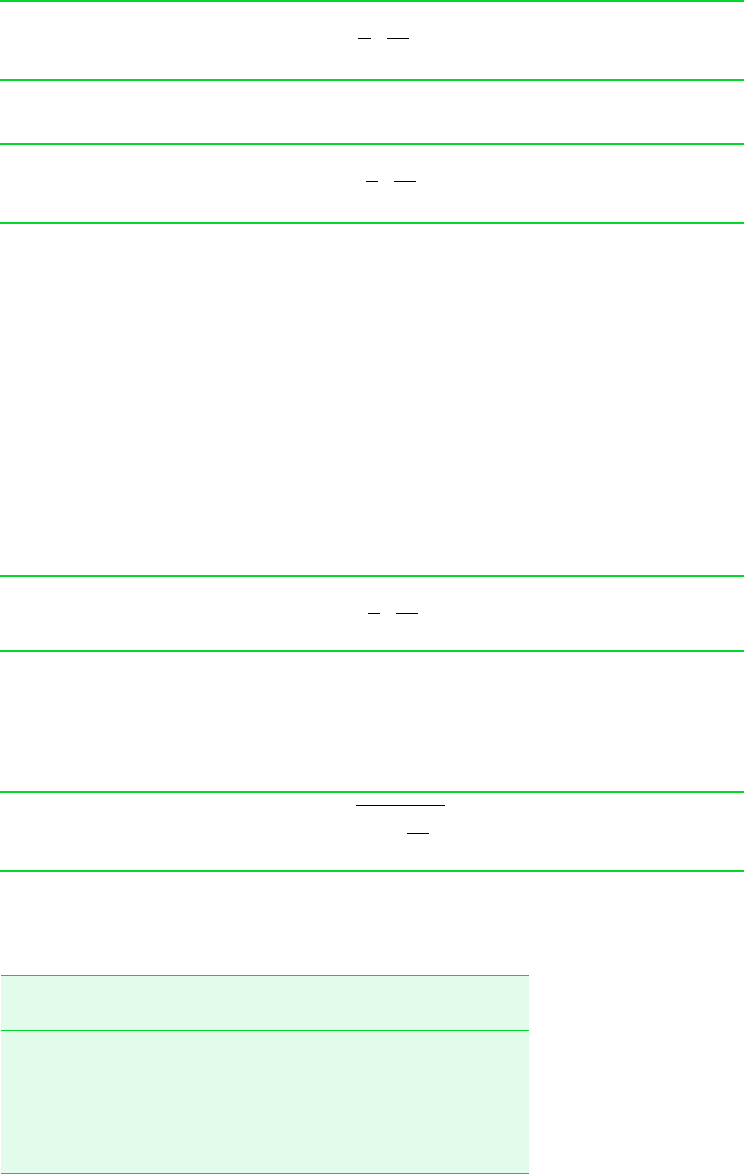
Schematic and Given Data:

Isotherm

 Figure E11.5

Analysis: The Redlich–Kwong equation of state is explicit in pressure, so Eqs. 11.50 and 11.51 are selected for determin-

ing s

 s

and u

 u

. Since T

 T

, an isothermal path of integration between the two states is convenient. Thus, these

equations reduce to give

 u





cT a

 p d dv

 s





Assumption: The Redlich–Kwong equation of state represents the p–v–T

behavior at these states and yields accurate values for (0p0T )

11.5 Other Thermodynamic Relations 513

The limits for each of the foregoing integrals are the specific volumes v

and v

at the two states under consideration.

Using p

, p

, and the known temperature, these specific volumes would be determined from the Redlich–Kwong equation of

state. Since this equation is not explicit in specific volume, the use of an equation solver such as Interactive Thermodynamics:

IT is recommended.

The above integrals involve the partial derivative (0p0T )

, which can be determined from the Redlich–Kwong equation

of state as

Inserting this into the expression for (s

 s

) gives

With the Redlich–Kwong equation, the integrand of the expression for (u

 u

) becomes

Accordingly

Finally, (h

 h

) would be determined using Eq. 11.61 together with the known values of (u

 u

), p

, v

, p

, and v



2 bT



cln

 ln a

 b

bd

2 bT



ln c

 b2

 u





2v1v  b2 T



dv 

2 bT







v  b

b dv



2v1v  b2 T



cT a

 p d T c

v  b



2v1v  b2 T



d c

v  b



v1v  b2 T



 R ln a

 b

b

2 bT



ln c

 b2

 R ln a

 b

b

2bT



cln a

b ln a

 b





v  b



2bT





v  b

bd dv

 s





v  b



2v1v  b2 T



d dv



v  b



2v1v  b2 T





11.5 Other Thermodynamic Relations

The presentation to this point has been directed mainly at developing thermodynamic relations

that allow changes in u, h, and s to be evaluated from measured property data. The object of

the present section is to introduce several other thermodynamic relations that are useful for

thermodynamic analysis. Each of the properties considered has a common attribute: it is de-

fined in terms of a partial derivative of some other property. The specific heats c

and c

are

examples of this type of property.

 11.5.1 Volume Expansivity, Isothermal and

Isentropic Compressibility

In single-phase regions, pressure and temperature are independent, and we can think of the spe-

cific volume as being a function of these two, v  v(T, p). The differential of such a function is

dv  a

dT  a

514 Chapter 11 Thermodynamic Relations

Two thermodynamic properties related to the partial derivatives appearing in this differ-

ential are the volume expansivity , also called the coefficient of volume expansion

(11.62)

and the isothermal compressibility 

(11.63)

By inspection, the unit for  is seen to be the reciprocal of that for temperature and the unit

for  is the reciprocal of that for pressure. The volume expansivity is an indication of the

change in volume that occurs when temperature changes while pressure remains constant.

The isothermal compressibility is an indication of the change in volume that takes place when

pressure changes while temperature remains constant. The value of  is positive for all sub-

stances in all phases.

The volume expansivity and isothermal compressibility are thermodynamic properties,

and like specific volume are functions of T and p. Values for  and  are provided in hand-

books of engineering data. Table 11.2 gives values of these properties for liquid water at a

pressure of 1 atm versus temperature. For a pressure of 1 atm, water has a state of maximum

density at about 4C. At this state, the value of  is zero.

The isentropic compressibility  is an indication of the change in volume that occurs

when pressure changes while entropy remains constant

(11.64)

The unit for  is the reciprocal of that for pressure.

The isentropic compressibility is related to the speed at which sound travels in the sub-

stance, and such speed measurements can be used to determine . In Sec. 9.12, the velocity

of sound, or sonic velocity, is introduced as

(9.36b)c 

v

a 

k 

b 

volume expansivity

isothermal

compressibility

velocity of sound

isentropic compressibility

TABLE 11.2 Volume Expansivity  and Isothermal Compressibility

 of Liquid Water at 1 atm versus Temperature

T Density   10

  10

(C) (kg/m

) (K)

1

(bar)

1

0 999.84 68.14 50.89

10 999.70 87.90 47.81

20 998.21 206.6 45.90

30 995.65 303.1 44.77

40 992.22 385.4 44.24

50 988.04 457.8 44.18

11.5 Other Thermodynamic Relations 515

The relationship of the isentropic compressibility and the velocity of sound can be obtained

using the relation between partial derivatives expressed by Eq. 11.15. Identifying p with x, v

with y, and s with z, we have

With this, the previous two equations can be combined to give

(11.65)

The details are left as an exercise.

 11.5.2 Relations Involving Specific Heats

In this section, general relations are obtained for the difference between specific heats (c

 c

)

and the ratio of specific heats c

c

EVALUATING (c

ⴚ c

). An expression for the difference between c

and c

can be obtained

by equating the two differentials for entropy given by Eqs. 11.48 and 11.57 and rearranging

to obtain

Considering the equation of state p  p(T, v), the differential dp can be expressed as

Eliminating dp between the last two equations and collecting terms gives

Since temperature and specific volume can be varied independently, the coefficients of the

differentials in this expression must vanish, so

(11.66)

(11.67)

Introducing Eq. 11.67 into Eq. 11.66 gives

(11.68)

This equation allows c

to be calculated from observed values of c

, or conversely, knowing

only p–v–T data.  for example. . . for the special case of an ideal gas, Eq. 11.68 re-

duces to Eq. 3.44, as can readily be shown. 

The right side of Eq. 11.68 can be expressed in terms of the volume expansivity  and

the isothermal compressibility . Introducing Eqs. 11.62 and 11.63, we get

(11.69)

 c

 v

 c

T a

a

 c

 T a

c1c

 c

2 T a

d dT  T ca

 a

d dv

dp 

dT 

 c

2 dT  T a

dv  T a

c  1v





10v



0p2